2.1 两条直线的位置关系(第2课时)同步课件(共33张PPT)
文档属性
| 名称 | 2.1 两条直线的位置关系(第2课时)同步课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
2.1 两条直线的位置关系
(第2课时)
学习目标
1)理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线。
2)掌握点到直线的距离的概念,并会度量点到直线的距离。
3)掌握垂线的性质,并会利用所学知识进行简单的计算。
重点
会用三角尺或量角器过一点画已知直线的垂线。
难点
掌握垂线的性质,并会利用所学知识进行简单的计算。
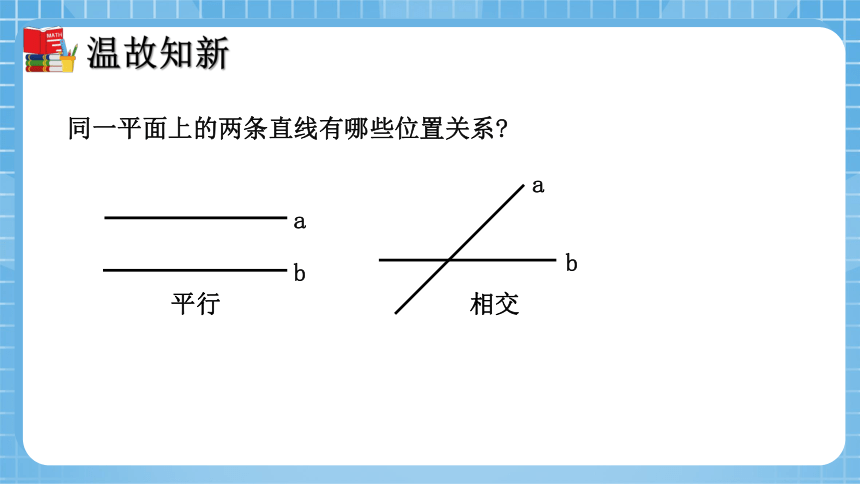
同一平面上的两条直线有哪些位置关系
a
b
平行
a
b
相交
对顶角的定义:
对顶角的性质:
有一个公共顶点,并且两边互为反向延长线的两个角叫做对顶角。
对顶角相等。
如果两个角的和等于180°,就说这两个角互为补角(简称互补)。
补角的定义:
如果两个角的和等于90°,就说这两个角互为余角(简称互余)。
余角的定义:
补角的性质:
同角或等角的补角相等。
余角的性质:
同角或等角的余角相等。
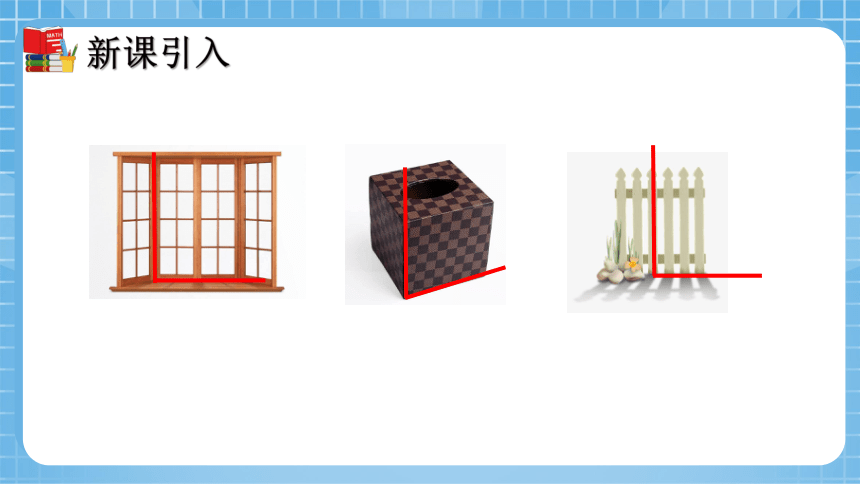
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
日常生活中,如图中的两条直线的关系很常见,你能再举出其他例子吗?
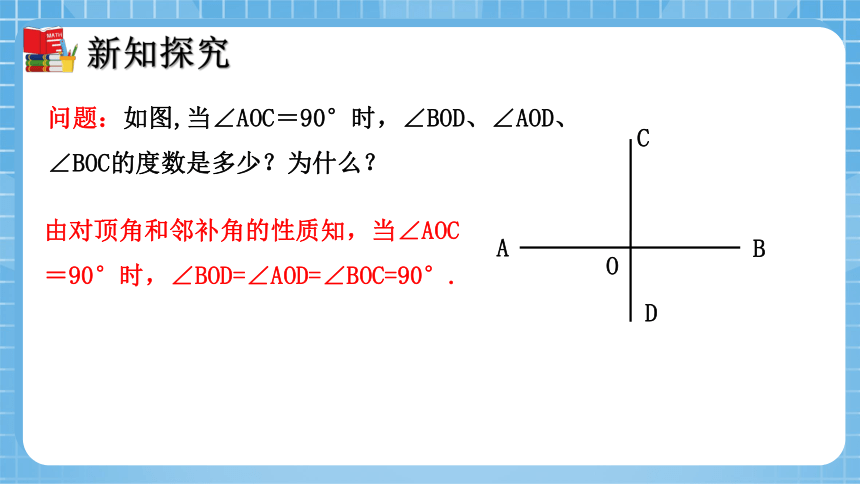
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC的度数是多少?为什么?
A
B
C
D
O
由对顶角和邻补角的性质知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
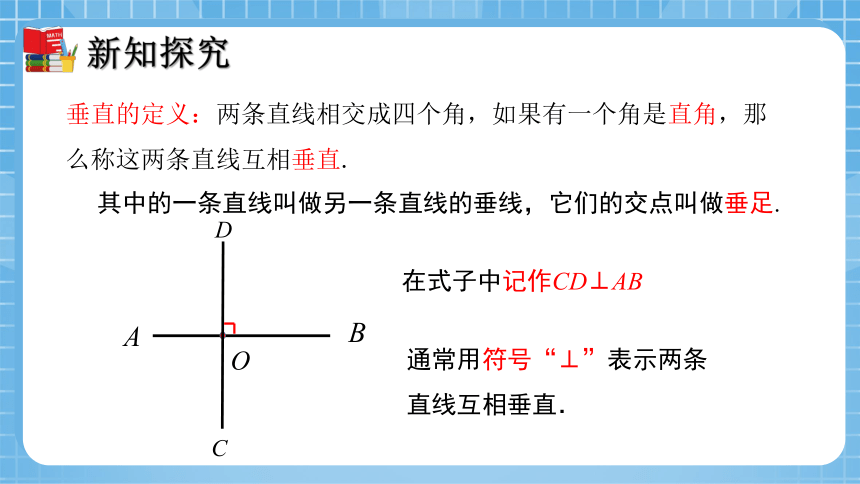
垂直的定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
通常用符号“⊥”表示两条直线互相垂直.
在式子中记作CD⊥AB
(1)如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
(2)如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:l⊥m(或m⊥l).
(3)把互相垂直的两条直线的交点叫作垂足(如图中的O点).
A
B
C
D
O
l
m
1、垂直的表示法
A
B
C
D
O
符号语言:
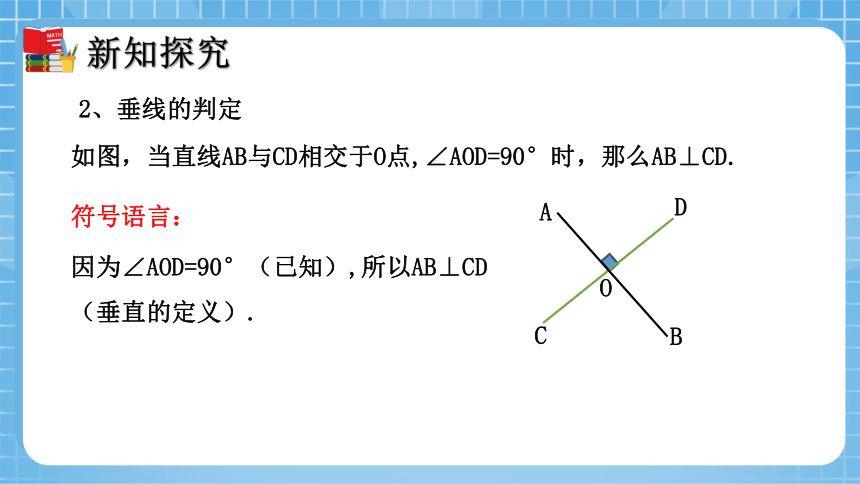
如图,当直线AB与CD相交于O点,∠AOD=90°时,那么AB⊥CD.
因为∠AOD=90°(已知),所以AB⊥CD(垂直的定义).
2、垂线的判定
两条直线互相垂直是两条直线相交的一种特殊情况
特殊性1:相交所成的四个角都等于90°
特殊性4:记作:AB⊥CD(或CD⊥AB),垂足为O; m⊥l(或l⊥m);
读作:直线AB垂直于直线CD,垂足为O
特殊性2:交点有专有名字:垂足
特殊性3:画图表示方法独特
O
D
C
B
A
l
m
O
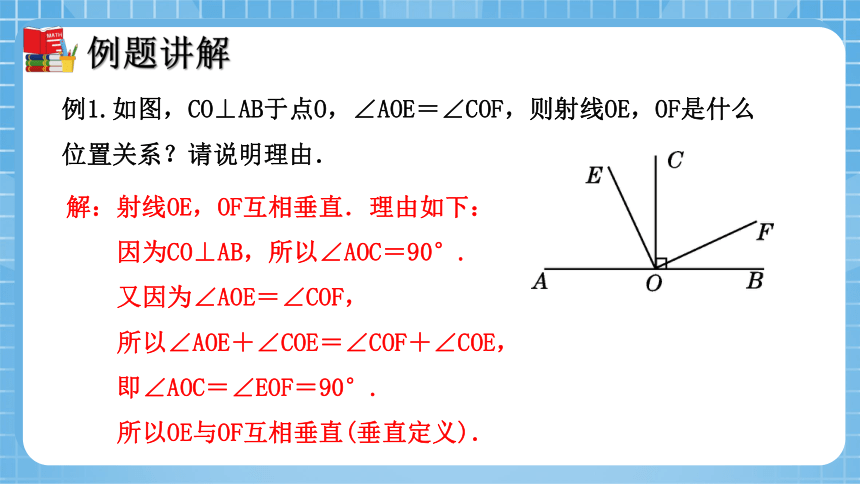
例1.如图,CO⊥AB于点O,∠AOE=∠COF,则射线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
(1)你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
(2)如果只有直尺,你能在下图方格纸上画出两条互相垂直的直线吗?
(3)你能通过折叠折出两条互相垂直的直线吗?
1.折叠长方形纸片的一个角;
2.沿①中的折痕对折,使它与①中的折痕互相重合;
3.展开长方形纸片,则两次折叠所形成的折痕互相垂直.
问题1:(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
A和直线l的位置关系有两种:点A可能在直线l上,也可能在直线l外.
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直.
注意:
b
a
O
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
3.这个结论仅限于平面内,否则不成立.
2.“有且只有”指的是存在且唯一;
c
例2.如图,已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
C
问题2:点P是直线l外一点,PO⊥l,点O是垂足,点A,B,C在直线l上,比较线段PO,PA,PB,PC的长短,你发现了什么?
l
O
C
B
A
P
线段PO的长度叫做点P到直线l的距离.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
l
O
C
B
A
P
线段AD的长度叫做点A到直线l的距离.
特别规定:
1. 如图,AO⊥CO,直线BD经过点O,且∠1=20°,则∠COD的度数为( )
A. 70° B. 110°
C. 140° D. 160°
B
2.如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B.45°
C.55° D.65°
3. 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
A. 28°
B. 60°
C. 62°
D. 152°
C
(考查垂线的定义及性质)
4.(2022春·福建福州·七年级校考期中)如图,点在直线上,.若,则的大小为( )
A. B. C. D.
【详解】解:∵点在直线上,,
∴,,
∵,
∴
∴;
故选A.
5.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )
6.如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条
直线与已知直线垂直
C.在同一平面内,过一点有且只有一条
直线与已知直线垂直
D.两点之间,线段最短
(考查垂线的定义及性质)
7.(2022春·河北邯郸·七年级校考期末)如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
【详解】解:∵射线OM平分∠AOC,∠AOM=35°,∴∠MOC=35°,
∵ON⊥OM,∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
故选:C
(考查垂线的定义及性质)
8.(2021春·河北沧州·七年级统考期末)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为_____°.
【详解】解:∵∠BOD:∠COM=1:3,OM⊥AB,∴∠BOM=90°,
∴∠BOD=,
∵∠AOB=180°,∴∠AOD=∠AOB-∠BOD=157.5°
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直,
(2)垂线段最短.
4.点到直线的距离
习题2.2
第2、3题
2.1 两条直线的位置关系
(第2课时)
学习目标
1)理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线。
2)掌握点到直线的距离的概念,并会度量点到直线的距离。
3)掌握垂线的性质,并会利用所学知识进行简单的计算。
重点
会用三角尺或量角器过一点画已知直线的垂线。
难点
掌握垂线的性质,并会利用所学知识进行简单的计算。
同一平面上的两条直线有哪些位置关系
a
b
平行
a
b
相交
对顶角的定义:
对顶角的性质:
有一个公共顶点,并且两边互为反向延长线的两个角叫做对顶角。
对顶角相等。
如果两个角的和等于180°,就说这两个角互为补角(简称互补)。
补角的定义:
如果两个角的和等于90°,就说这两个角互为余角(简称互余)。
余角的定义:
补角的性质:
同角或等角的补角相等。
余角的性质:
同角或等角的余角相等。
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
日常生活中,如图中的两条直线的关系很常见,你能再举出其他例子吗?
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC的度数是多少?为什么?
A
B
C
D
O
由对顶角和邻补角的性质知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
垂直的定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
通常用符号“⊥”表示两条直线互相垂直.
在式子中记作CD⊥AB
(1)如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
(2)如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:l⊥m(或m⊥l).
(3)把互相垂直的两条直线的交点叫作垂足(如图中的O点).
A
B
C
D
O
l
m
1、垂直的表示法
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,那么AB⊥CD.
因为∠AOD=90°(已知),所以AB⊥CD(垂直的定义).
2、垂线的判定
两条直线互相垂直是两条直线相交的一种特殊情况
特殊性1:相交所成的四个角都等于90°
特殊性4:记作:AB⊥CD(或CD⊥AB),垂足为O; m⊥l(或l⊥m);
读作:直线AB垂直于直线CD,垂足为O
特殊性2:交点有专有名字:垂足
特殊性3:画图表示方法独特
O
D
C
B
A
l
m
O
例1.如图,CO⊥AB于点O,∠AOE=∠COF,则射线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
(1)你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
(2)如果只有直尺,你能在下图方格纸上画出两条互相垂直的直线吗?
(3)你能通过折叠折出两条互相垂直的直线吗?
1.折叠长方形纸片的一个角;
2.沿①中的折痕对折,使它与①中的折痕互相重合;
3.展开长方形纸片,则两次折叠所形成的折痕互相垂直.
问题1:(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
A和直线l的位置关系有两种:点A可能在直线l上,也可能在直线l外.
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直.
注意:
b
a
O
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
3.这个结论仅限于平面内,否则不成立.
2.“有且只有”指的是存在且唯一;
c
例2.如图,已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
C
问题2:点P是直线l外一点,PO⊥l,点O是垂足,点A,B,C在直线l上,比较线段PO,PA,PB,PC的长短,你发现了什么?
l
O
C
B
A
P
线段PO的长度叫做点P到直线l的距离.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
l
O
C
B
A
P
线段AD的长度叫做点A到直线l的距离.
特别规定:
1. 如图,AO⊥CO,直线BD经过点O,且∠1=20°,则∠COD的度数为( )
A. 70° B. 110°
C. 140° D. 160°
B
2.如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B.45°
C.55° D.65°
3. 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
A. 28°
B. 60°
C. 62°
D. 152°
C
(考查垂线的定义及性质)
4.(2022春·福建福州·七年级校考期中)如图,点在直线上,.若,则的大小为( )
A. B. C. D.
【详解】解:∵点在直线上,,
∴,,
∵,
∴
∴;
故选A.
5.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )
6.如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条
直线与已知直线垂直
C.在同一平面内,过一点有且只有一条
直线与已知直线垂直
D.两点之间,线段最短
(考查垂线的定义及性质)
7.(2022春·河北邯郸·七年级校考期末)如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
【详解】解:∵射线OM平分∠AOC,∠AOM=35°,∴∠MOC=35°,
∵ON⊥OM,∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
故选:C
(考查垂线的定义及性质)
8.(2021春·河北沧州·七年级统考期末)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为_____°.
【详解】解:∵∠BOD:∠COM=1:3,OM⊥AB,∴∠BOM=90°,
∴∠BOD=,
∵∠AOB=180°,∴∠AOD=∠AOB-∠BOD=157.5°
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直,
(2)垂线段最短.
4.点到直线的距离
习题2.2
第2、3题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
