5.2 视图 第2课时 课件(共18张PPT) 北师大版九年级上册数学
文档属性
| 名称 | 5.2 视图 第2课时 课件(共18张PPT) 北师大版九年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 787.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第五章 投影与视图
2 视图 第2课时
1.通过画直棱柱的三视图,体会直棱柱与其三视图之间的相互转化.
2.经历探索简单的几何体三视图的还原过程,初步建立空间观念,能将三视图转换成立体图形进一步培养空间想象能力.
3.能根据物体的三视图描述出基本几何体或实物原型,并进行一些简单的计算和运用.
◎重点:由三视图描述立体图形,并把三视图中所标的数据对应到立体图形之中.
激趣导入
观察:请同学们拿出事先准备好的直三棱柱、直四棱柱,根据你所摆放的位置经过想象,再抽象出这两个直棱柱的主视图,左视图和俯视图.
绘制:请你将抽象出来的三种视图画出来,并与同伴交流.
比较:小亮画出了其中一个几何体的主视图、左视图和俯视图,你认为他画的对不对?谈谈你的看法.
拓展:当你手中的两个直棱柱摆放的角度变化时,它们的三种视图是否会随之改变?试一试.
画直棱柱的三视图
阅读教材本课时“习题5.4”前面的内容,完成下列问题.
在画视图时,注意:(1)在观察时,视线一定要与观察面 垂直 ;(2)一定要将 边缘 、 棱 、 顶点 都体现出来,同时看得见的轮廓线画成 实线 ,看不见的轮廓线画成 虚线 ;(3)按三视图的位置与大小要求从整体上画出几何体的三视图.
垂直
边缘
棱
顶点
实线
虚
线
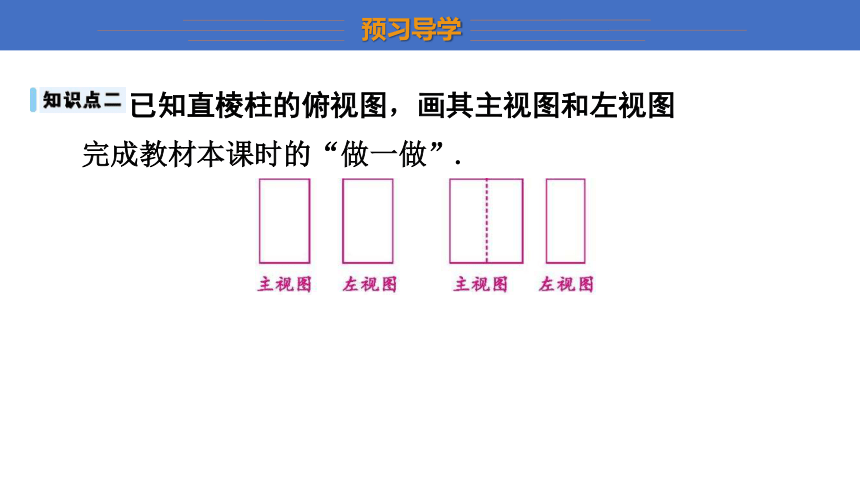
已知直棱柱的俯视图,画其主视图和左视图
完成教材本课时的“做一做”.
根据三视图还原几何体
阅读教材本课时“习题5.5”前的内容,完成下列问题.
由三视图想象几何体的形状,一般是由俯视图确定物体在 平面上 的形状,根据左视图、主视图想象出它在 空间里 的形状,即根据主视图、俯视图和左视图想象几何体的 前面 、 上面 和 左侧面 的形状,然后综合起来考虑整体形状.
平面上
空间里
前
面
上面
左侧面
·导学建议·
1.在教学方法和手段上主要使用体验法和讨论法.体验法就是学生亲历观察,感受探索发现和经验积累的乐趣,内化教学内容的方法.
2.通过学生熟悉的问题引起学生对旧知的回顾,联系七年级学过的从上看、从左看、从前看,强化学生对三视图描述实物图的认识.
1. 一个用小立方块搭成的几何体的主视图和左视图都如图所示,则这个小几何体中小立方块最少有 3 块.
3
2.某工厂要加工一批上下底密封纸盒,设计者给出了如图1所示的密封纸盒的三视图.
(1)由三视图可知,密封纸盒的形状是 ;
(2)根据该几何体的三视图,在图2中补全它的表面展开图.
解:(1)(正)六棱柱.
(2)六棱柱的表面展开图如图.
一个几何体的三视图如图所示,那么这个几何体是( A )
A B C D
A
有一个铁制零件(正方体中间挖去一个圆柱体形状的孔)按如图所示的方式放置,则它的左视图是( C )
A B C D
C
在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来(如图),则这堆正方体货箱共有( B )
A.4箱 B.5箱
C.6箱 D.7箱
B
变式训练 如图,这分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是( B )
A.3或4 B.4或5
C.5或6 D.6或7
B
根据物体的三种视图(如图),描述物体的形状,并画出图形.
解:如图,该物体是五棱柱.
已知正六棱柱的俯视图如图所示,请你画出它的主视图和左视图.
解:答案不唯一,可以是如图所示.
方法归纳交流 由三视图还原小正方体的个数主要有两种思路:一是根据三视图,发挥空间想象能力,判断出几何体的列数及各列的最高层数;二是通过动手操作,根据给出的三视图,利用小正方体堆成几何体,根据实物得到答案.
如图,这是由一些大小相同的小正方体搭成的几何体的主视图和俯视图,则搭成该几何体的小正方体最多是 7 个.
7
第五章 投影与视图
2 视图 第2课时
1.通过画直棱柱的三视图,体会直棱柱与其三视图之间的相互转化.
2.经历探索简单的几何体三视图的还原过程,初步建立空间观念,能将三视图转换成立体图形进一步培养空间想象能力.
3.能根据物体的三视图描述出基本几何体或实物原型,并进行一些简单的计算和运用.
◎重点:由三视图描述立体图形,并把三视图中所标的数据对应到立体图形之中.
激趣导入
观察:请同学们拿出事先准备好的直三棱柱、直四棱柱,根据你所摆放的位置经过想象,再抽象出这两个直棱柱的主视图,左视图和俯视图.
绘制:请你将抽象出来的三种视图画出来,并与同伴交流.
比较:小亮画出了其中一个几何体的主视图、左视图和俯视图,你认为他画的对不对?谈谈你的看法.
拓展:当你手中的两个直棱柱摆放的角度变化时,它们的三种视图是否会随之改变?试一试.
画直棱柱的三视图
阅读教材本课时“习题5.4”前面的内容,完成下列问题.
在画视图时,注意:(1)在观察时,视线一定要与观察面 垂直 ;(2)一定要将 边缘 、 棱 、 顶点 都体现出来,同时看得见的轮廓线画成 实线 ,看不见的轮廓线画成 虚线 ;(3)按三视图的位置与大小要求从整体上画出几何体的三视图.
垂直
边缘
棱
顶点
实线
虚
线
已知直棱柱的俯视图,画其主视图和左视图
完成教材本课时的“做一做”.
根据三视图还原几何体
阅读教材本课时“习题5.5”前的内容,完成下列问题.
由三视图想象几何体的形状,一般是由俯视图确定物体在 平面上 的形状,根据左视图、主视图想象出它在 空间里 的形状,即根据主视图、俯视图和左视图想象几何体的 前面 、 上面 和 左侧面 的形状,然后综合起来考虑整体形状.
平面上
空间里
前
面
上面
左侧面
·导学建议·
1.在教学方法和手段上主要使用体验法和讨论法.体验法就是学生亲历观察,感受探索发现和经验积累的乐趣,内化教学内容的方法.
2.通过学生熟悉的问题引起学生对旧知的回顾,联系七年级学过的从上看、从左看、从前看,强化学生对三视图描述实物图的认识.
1. 一个用小立方块搭成的几何体的主视图和左视图都如图所示,则这个小几何体中小立方块最少有 3 块.
3
2.某工厂要加工一批上下底密封纸盒,设计者给出了如图1所示的密封纸盒的三视图.
(1)由三视图可知,密封纸盒的形状是 ;
(2)根据该几何体的三视图,在图2中补全它的表面展开图.
解:(1)(正)六棱柱.
(2)六棱柱的表面展开图如图.
一个几何体的三视图如图所示,那么这个几何体是( A )
A B C D
A
有一个铁制零件(正方体中间挖去一个圆柱体形状的孔)按如图所示的方式放置,则它的左视图是( C )
A B C D
C
在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来(如图),则这堆正方体货箱共有( B )
A.4箱 B.5箱
C.6箱 D.7箱
B
变式训练 如图,这分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是( B )
A.3或4 B.4或5
C.5或6 D.6或7
B
根据物体的三种视图(如图),描述物体的形状,并画出图形.
解:如图,该物体是五棱柱.
已知正六棱柱的俯视图如图所示,请你画出它的主视图和左视图.
解:答案不唯一,可以是如图所示.
方法归纳交流 由三视图还原小正方体的个数主要有两种思路:一是根据三视图,发挥空间想象能力,判断出几何体的列数及各列的最高层数;二是通过动手操作,根据给出的三视图,利用小正方体堆成几何体,根据实物得到答案.
如图,这是由一些大小相同的小正方体搭成的几何体的主视图和俯视图,则搭成该几何体的小正方体最多是 7 个.
7
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
