第12章一次函数期末复习(5)分段函数问题 课件(共21张PPT)
文档属性
| 名称 | 第12章一次函数期末复习(5)分段函数问题 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 136.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览


文档简介
(共21张PPT)
第12章 一次函数 期末复习 (5)
分段函数问题
(1)用一次函数的图象寻求实际问题中的变化规律解题.
(2)利用两个一次函数的图象解决方案选择问题.
用一次函数解决实际问题
常考角度
1.分段函数问题(分段价格、几何动点)由形求式
(单个函数图象、多个函数图象)
2.方案设计问题(物资调运、方案比较).
3.一次函数最值问题.
复习要点
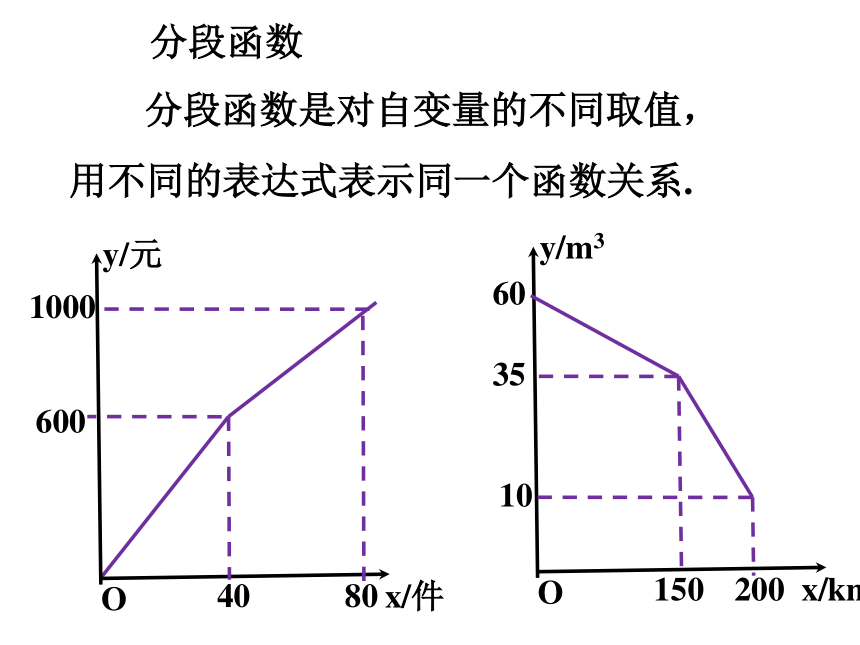
分段函数
分段函数是对自变量的不同取值,
用不同的表达式表示同一个函数关系.
y/元
x/件
O
40
80
600
1000
y/m3
x/km
O
150
200
10
60
35
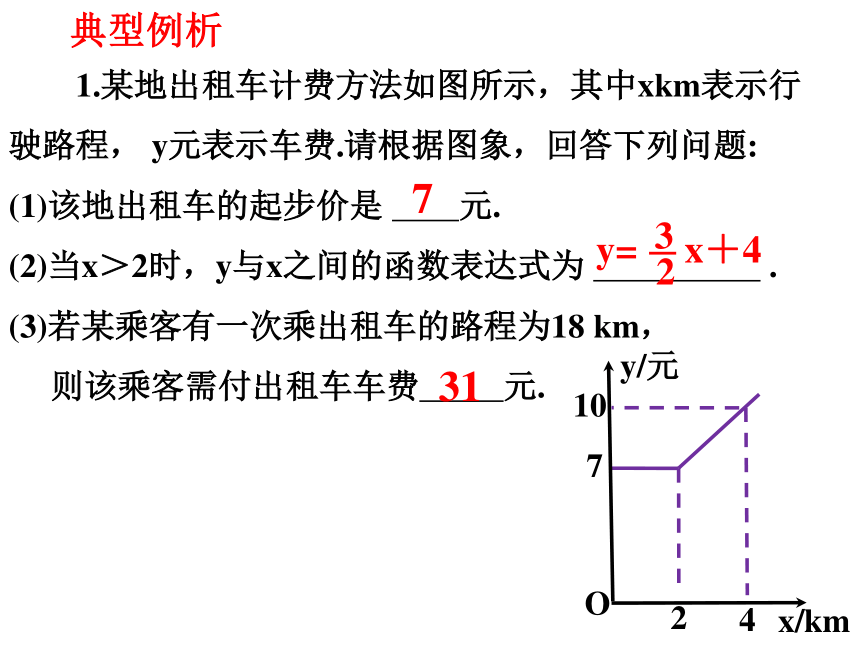
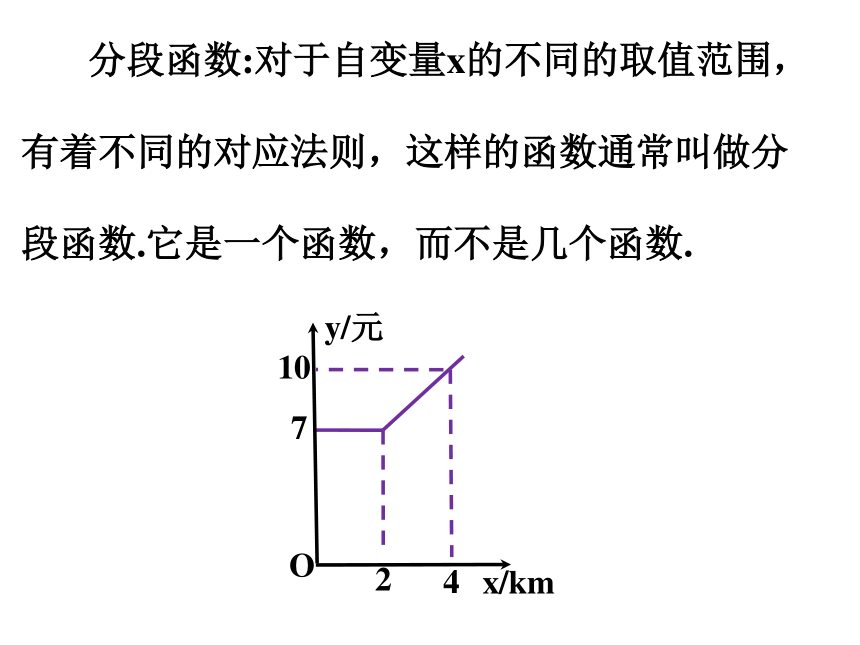
1.某地出租车计费方法如图所示,其中xkm表示行驶路程, y元表示车费.请根据图象,回答下列问题:
(1)该地出租车的起步价是 元.
(2)当x>2时,y与x之间的函数表达式为 .
(3)若某乘客有一次乘出租车的路程为18 km,
则该乘客需付出租车车费 元.
y/元
x/km
O
2
4
7
10
7
31
y= x+4
3
2
典型例析
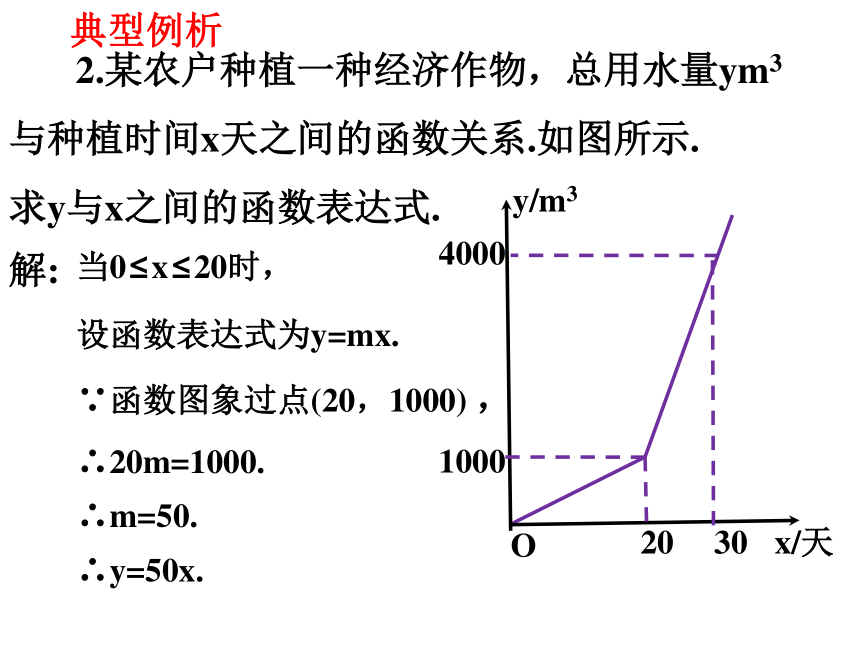
2.某农户种植一种经济作物,总用水量ym3与种植时间x天之间的函数关系.如图所示.
求y与x之间的函数表达式.
y/m3
x/天
O
20
30
1000
4000
解:
∵函数图象过点(20,1000) ,
当0≤x≤20时,
设函数表达式为y=mx.
∴20m=1000.
∴m=50.
∴y=50x.
典型例析
y/m3
x/天
O
20
30
1000
4000
∵函数图象过点(20,1000) 和(30,4000),
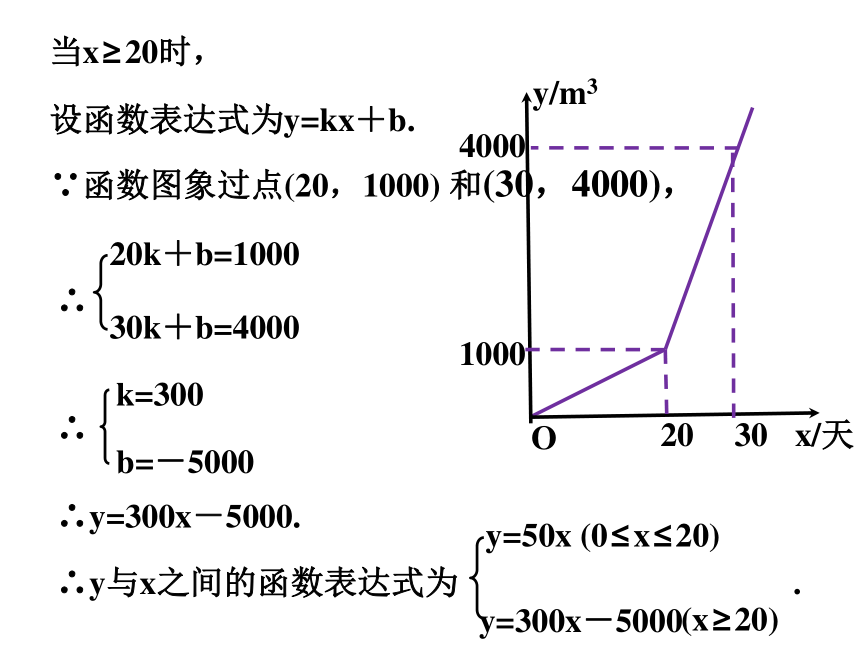
当x≥20时,
设函数表达式为y=kx+b.
∴
∴
∴y=300x-5000.
∴y与x之间的函数表达式为 .
20k+b=1000
30k+b=4000
k=300
b=-5000
y=50x
y=300x-5000
(0≤x≤20)
(x≥20)
分段函数:对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.
y/元
x/km
O
2
4
7
10
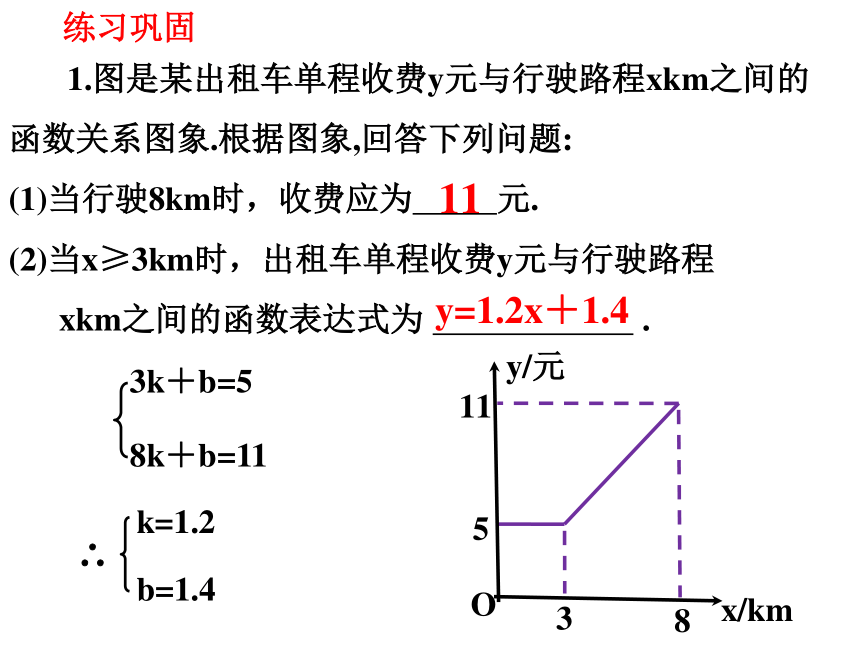
1.图是某出租车单程收费y元与行驶路程xkm之间的函数关系图象.根据图象,回答下列问题:
(1)当行驶8km时,收费应为 元.
(2)当x≥3km时,出租车单程收费y元与行驶路程
xkm之间的函数表达式为 .
y/元
x/km
O
3
8
5
11
11
y=1.2x+1.4
∴
3k+b=5
8k+b=11
k=1.2
b=1.4
练习巩固
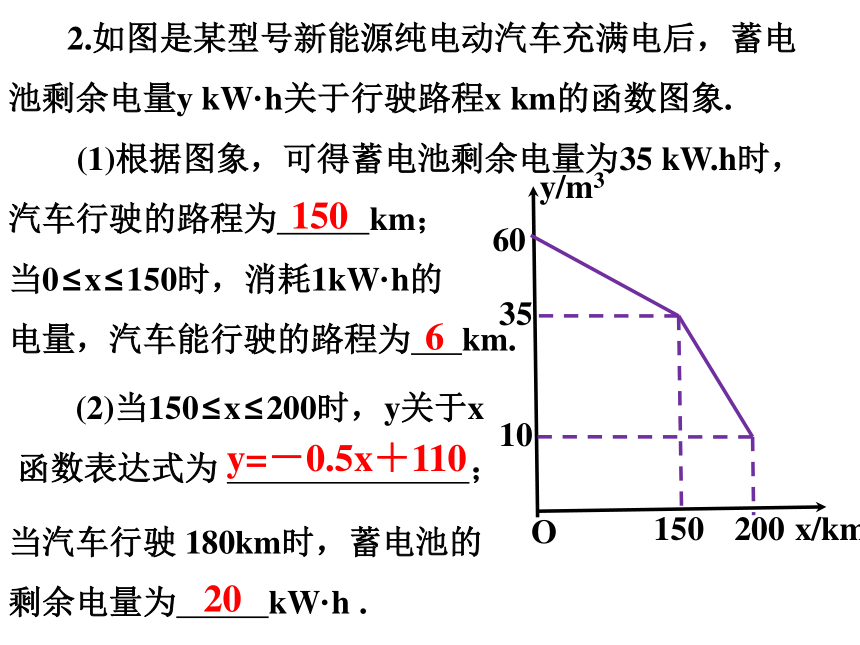
2.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y kW·h关于行驶路程x km的函数图象. (1)根据图象,可得蓄电池剩余电量为35 kW.h时,汽车行驶的路程为 km;
当0≤x≤150时,消耗1kW·h的
电量,汽车能行驶的路程为 km.
y/m3
x/km
O
150
200
10
60
35
(2)当150≤x≤200时,y关于x
函数表达式为 ;
当汽车行驶 180km时,蓄电池的
剩余电量为 kW·h .
150
6
y=-0.5x+110
20
3.某图书馆对外出租书的收费方式是每本书出租后的前两天,每天收0.6元,以后每天收0.3元,那么一本书在出租x天(x≥2)后,所收租金y元与天数x的函数表达式为 .
y=0.3x+0.6
当x≥2时,
y=1.2+0.3(x-2)
4. 小明以每件6元的价格购进某商品若干件到市场销售,销售金额y元与销售量x件之间的函数关系如图所示,则降价后每件商品销售的价格为( ).
A.5元 B.10元
C.12.5元 D.15 元
y/元
x/件
O
40
80
600
1000
5.为增强居民的节水意识,某市自2023年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(m3)的函数关系的图象如图所示.如果某个家庭2023年全年上缴水费1180元,那么该家庭2023年用水的总量是( ).
A.240m3 B.236m3
C.220m3 D.200m3
y/元
x/m3
O
180
260
900
1460
C
6. 一个试验室在0:00 — 2:00保持20 ℃的恒温,在2:00 — 4:00匀速升温,每小时升高5 ℃ 。写出试验室温度 T(单位: ℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
解:
当0:00≤t≤2:00时,
当2:00≤t≤4:00时,
T=20;
T=5t+10.
O
2
20
t
T
(h)
( ℃)
4
T=5t+10.
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
7.“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填出下表:
2.5
5
7.5
10
12
14
16
18
7. “黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(2)写出付款金额 y(单位:元)与购买种子数量x(单位:kg)之间的函数解析式,并画出函数图象.
当0≤x≤2时,
解:
y=
5x;
当x>2时,
y=
2×5
+
(x-2)
×5×0.8
y=4x+2
当0≤x≤2时,
解:
y=5x
当x>2时,
y=4x+2
O
2
10
x
y
y=4x+2
8.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元.设托运为pkg(p为整数)物品的费用为c.试写出c的计算公式.
解:c的计算公式为:
即:
c=0.5(p-1)+2
c=2
c=0.5p+1.5
c=2
(0<p≤1),
(p>1).
(0<p≤1),
(p>1).
9.某中学数学课外活动小组从网上获取该市企业职工养老保险金个人月缴费y元随个人月工资x元变化的图象.请根据图象解答下面的问题:
(1)张总工程师10月份工资是12000元,这个月他
个人应缴养老保险金多少元?
(2)小刘10月份工资3000元,这个月他个人应缴养
老保险 金多少元?
(3)李师傅10月份个人缴养老保险金240元,求
他10月份的工资是多少元?(写出解答过程)
(1)张总工程师10月份工资是12000元,这个月他
个人 应缴养老保险金多少元?
解:(1)张总工程师10月份个人应缴养老
保险金 487.73元.
x/元
y/元
162.58
487.73
3387
1010
O
10161
(2)小刘10月份工资3000元,这个月他个人应养
老保险金多少元?
(2)小刘10月份他个人应缴养老保险金162.58元.
x/元
y/元
162.58
487.73
3387
1010
O
10161
x/元
y/元
162.58
487.73
3387
1010
O
10161
(3)李师傅10月份个人缴养老保险金240元,求他10月份
的工资是多少元?(写出解答过程)
根据题意,得
3387k+b=162.58
10161k+b=487.73
∴k=0.048,
240
b=0.
∴y=0.048x,
李师傅10月份的工资是5000元.
当y=240时,
x=5000.
(3) ∵保险金240元在162.58元与487.73元之间,这段月保险金数y元与月工资数x元从图象看,成一次函数关系,
∴可设为y=kx+b.
第12章 一次函数 期末复习 (5)
分段函数问题
(1)用一次函数的图象寻求实际问题中的变化规律解题.
(2)利用两个一次函数的图象解决方案选择问题.
用一次函数解决实际问题
常考角度
1.分段函数问题(分段价格、几何动点)由形求式
(单个函数图象、多个函数图象)
2.方案设计问题(物资调运、方案比较).
3.一次函数最值问题.
复习要点
分段函数
分段函数是对自变量的不同取值,
用不同的表达式表示同一个函数关系.
y/元
x/件
O
40
80
600
1000
y/m3
x/km
O
150
200
10
60
35
1.某地出租车计费方法如图所示,其中xkm表示行驶路程, y元表示车费.请根据图象,回答下列问题:
(1)该地出租车的起步价是 元.
(2)当x>2时,y与x之间的函数表达式为 .
(3)若某乘客有一次乘出租车的路程为18 km,
则该乘客需付出租车车费 元.
y/元
x/km
O
2
4
7
10
7
31
y= x+4
3
2
典型例析
2.某农户种植一种经济作物,总用水量ym3与种植时间x天之间的函数关系.如图所示.
求y与x之间的函数表达式.
y/m3
x/天
O
20
30
1000
4000
解:
∵函数图象过点(20,1000) ,
当0≤x≤20时,
设函数表达式为y=mx.
∴20m=1000.
∴m=50.
∴y=50x.
典型例析
y/m3
x/天
O
20
30
1000
4000
∵函数图象过点(20,1000) 和(30,4000),
当x≥20时,
设函数表达式为y=kx+b.
∴
∴
∴y=300x-5000.
∴y与x之间的函数表达式为 .
20k+b=1000
30k+b=4000
k=300
b=-5000
y=50x
y=300x-5000
(0≤x≤20)
(x≥20)
分段函数:对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.
y/元
x/km
O
2
4
7
10
1.图是某出租车单程收费y元与行驶路程xkm之间的函数关系图象.根据图象,回答下列问题:
(1)当行驶8km时,收费应为 元.
(2)当x≥3km时,出租车单程收费y元与行驶路程
xkm之间的函数表达式为 .
y/元
x/km
O
3
8
5
11
11
y=1.2x+1.4
∴
3k+b=5
8k+b=11
k=1.2
b=1.4
练习巩固
2.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y kW·h关于行驶路程x km的函数图象. (1)根据图象,可得蓄电池剩余电量为35 kW.h时,汽车行驶的路程为 km;
当0≤x≤150时,消耗1kW·h的
电量,汽车能行驶的路程为 km.
y/m3
x/km
O
150
200
10
60
35
(2)当150≤x≤200时,y关于x
函数表达式为 ;
当汽车行驶 180km时,蓄电池的
剩余电量为 kW·h .
150
6
y=-0.5x+110
20
3.某图书馆对外出租书的收费方式是每本书出租后的前两天,每天收0.6元,以后每天收0.3元,那么一本书在出租x天(x≥2)后,所收租金y元与天数x的函数表达式为 .
y=0.3x+0.6
当x≥2时,
y=1.2+0.3(x-2)
4. 小明以每件6元的价格购进某商品若干件到市场销售,销售金额y元与销售量x件之间的函数关系如图所示,则降价后每件商品销售的价格为( ).
A.5元 B.10元
C.12.5元 D.15 元
y/元
x/件
O
40
80
600
1000
5.为增强居民的节水意识,某市自2023年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(m3)的函数关系的图象如图所示.如果某个家庭2023年全年上缴水费1180元,那么该家庭2023年用水的总量是( ).
A.240m3 B.236m3
C.220m3 D.200m3
y/元
x/m3
O
180
260
900
1460
C
6. 一个试验室在0:00 — 2:00保持20 ℃的恒温,在2:00 — 4:00匀速升温,每小时升高5 ℃ 。写出试验室温度 T(单位: ℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
解:
当0:00≤t≤2:00时,
当2:00≤t≤4:00时,
T=20;
T=5t+10.
O
2
20
t
T
(h)
( ℃)
4
T=5t+10.
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
7.“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填出下表:
2.5
5
7.5
10
12
14
16
18
7. “黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(2)写出付款金额 y(单位:元)与购买种子数量x(单位:kg)之间的函数解析式,并画出函数图象.
当0≤x≤2时,
解:
y=
5x;
当x>2时,
y=
2×5
+
(x-2)
×5×0.8
y=4x+2
当0≤x≤2时,
解:
y=5x
当x>2时,
y=4x+2
O
2
10
x
y
y=4x+2
8.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元.设托运为pkg(p为整数)物品的费用为c.试写出c的计算公式.
解:c的计算公式为:
即:
c=0.5(p-1)+2
c=2
c=0.5p+1.5
c=2
(0<p≤1),
(p>1).
(0<p≤1),
(p>1).
9.某中学数学课外活动小组从网上获取该市企业职工养老保险金个人月缴费y元随个人月工资x元变化的图象.请根据图象解答下面的问题:
(1)张总工程师10月份工资是12000元,这个月他
个人应缴养老保险金多少元?
(2)小刘10月份工资3000元,这个月他个人应缴养
老保险 金多少元?
(3)李师傅10月份个人缴养老保险金240元,求
他10月份的工资是多少元?(写出解答过程)
(1)张总工程师10月份工资是12000元,这个月他
个人 应缴养老保险金多少元?
解:(1)张总工程师10月份个人应缴养老
保险金 487.73元.
x/元
y/元
162.58
487.73
3387
1010
O
10161
(2)小刘10月份工资3000元,这个月他个人应养
老保险金多少元?
(2)小刘10月份他个人应缴养老保险金162.58元.
x/元
y/元
162.58
487.73
3387
1010
O
10161
x/元
y/元
162.58
487.73
3387
1010
O
10161
(3)李师傅10月份个人缴养老保险金240元,求他10月份
的工资是多少元?(写出解答过程)
根据题意,得
3387k+b=162.58
10161k+b=487.73
∴k=0.048,
240
b=0.
∴y=0.048x,
李师傅10月份的工资是5000元.
当y=240时,
x=5000.
(3) ∵保险金240元在162.58元与487.73元之间,这段月保险金数y元与月工资数x元从图象看,成一次函数关系,
∴可设为y=kx+b.
