第12章一次函数期末复习(6)方案选择问题 课件(共26张PPT)
文档属性
| 名称 | 第12章一次函数期末复习(6)方案选择问题 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 13:21:15 | ||
图片预览








文档简介
(共26张PPT)
第12章 一次函数 期末复习 (6)
方案选择问题
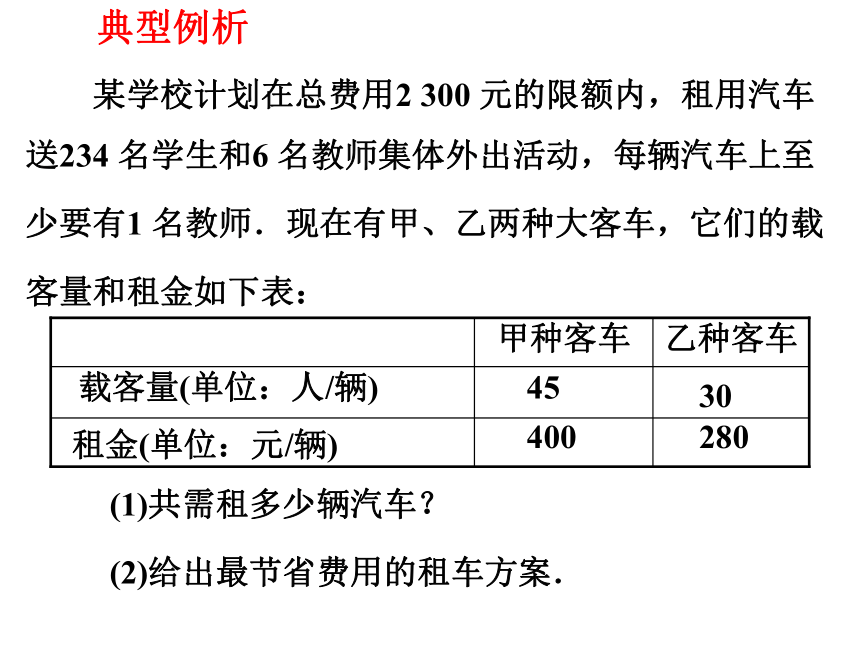
某学校计划在总费用2 300 元的限额内,租用汽车
送234 名学生和6 名教师集体外出活动,每辆汽车上至
少要有1 名教师.现在有甲、乙两种大客车,它们的载
客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
典型例析
问题1 影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
问题2 所租汽车辆数又与哪些因素有关?
与乘车人数有关.
问题3 如何由乘车人数确定租车辆数呢?
(2)要使每辆汽车上至少有1 名教师,汽车
总数不能大于 .
问题3 如何由乘车人数确定租车辆数呢?
(1)要保证240 名师生都有车坐,汽车
总数不能小于 ;
6 辆
6 辆
∴汽车总数为 .
6 辆
问题4 在汽车总数确定后,租车费用与租车的种类有关.如果租甲类车x 辆,能求出租车费用吗?
设租用 x 辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;
设租车费用为 y,
则
y =
400x
化简 得
y =
+
280(6-x)
120x+1 680.
k =
120
∴y 随着 x 的增大而增大,
> 0,
∴当甲类车取最少时,
租车费用y 为最少.
(1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
问题5 如何确定 y =120x+1 680中 y 的最小值.
45x+30(6-x)≥240
400x+280(6-x)≤2 300
由
得 4≤x≤ .
31
6
据实际意义可取4 或5;
∴当 x =4 时,
∵ y 随着 x 的增大而增大,
y 的最小值为2 160.
y 最小,
解:设租用x 辆甲种客车,则租用乙种客车的辆数
为(6-x)辆;设租车费用为 y,则
y =400x+280(6-x)
化简 得y =120x+1 680.
(1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
45x+30(6-x)≥240
400x+280(6-x)≤2 300
由
得 4≤x≤ .
据实际意义可取4 或5;
∵ y 随着 x 的增大而增大, ∴当 x =4 时,
y 最小,y 的最小值为2 160.
31
6
1.某中学为增强学生体质,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需510元;购买3个篮球和5个足球共需810元.
(1)求篮球和足球的单价分别是多少元.
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元,那么有哪几种购买方案
练习巩固
方案设计问题
解:(1)设篮球的单价为a元,足球的单价为b元.
根据题意,得
答:篮球的单价为120元,足球的单价为90元.
3a+5b=810.
2a+3b=510,
a=120,
b=90.
∴
(2)设采购篮球x个,则采购足球(50-x)个.
∵要求篮球不少于30个,且总费用不超过5500元,
∵ x为整数, ∴ x的值可为30,31,32,33.
因此共有四种购买方案.
方案一:采购篮球 30个,采购足球20个;
方案二:采购篮球31个, 采购足球19个;
方案三:采购篮球 32个,采购足球 18个;
方案四:采购篮球 33个,采购足球 17 个.
120x+90(50-x)≤5500
x≥30,
∴
∴
30≤x≤
100
3
-
2. 某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
2. 某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
解:(1)设 A、B 两种型号电动自行车的进货单价分别为 x 元、 (x+500)元.由题意:
解得 x=2500,
经检验:x=2500 是分式方程的解.
答:A、B 两种型号电动自行车的进货单价分别为 2500 元 ,3000 元.
x+500
50000
x
60000
=
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(2)y=300m+500(30-m)
=-200m+15000 (20≤m≤30),
(3)该商店如何进货才能获得最大利润?此时最大利润
是多少元?
(3)∵y=300m+500(30-m)
=-200m+15000,
∵k=-200<0,
∴ y随m的增大而减小,
∵ 20≤m≤30,
∴m=20 时,y 有最大值,最大值为 11000 元.
3.某单位准备购买文化用品,该文化用品在甲、乙两家超市的标价均为10元/件现甲、乙两家超市进行促销活动.
甲超市:一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖.
乙超市:全部按标价的8折售卖.
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为___元,在乙超市的购物金额为 元.
(2)假如你是该单位的采购员,为使支付的费用较少,你应该选择哪家超市购买
2.某单位准备购买文化用品,该文化用品在甲、乙两家超市的标价均为10元/件现甲、乙两家超市进行促销活动.
甲超市:一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖.
乙超市:全部按标价的8折售卖.
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为___ 元,在乙超市的购物金额为 元.
300
240
(2)设购买x件这种文化用品.
①当0在甲超市的购物金额为10x元,
在乙超市的购物金额为0.8×10x=8x(元),
∵ 10x>8x,所以选择乙超市购买.
②当x>40时,
在甲超市的购物金额为
400+0.6×(10x-400)=(6x +160)(元),
在乙超市的购物金额为
0.8×10x=8x(元)
若6x+160>8x,则40若6x+160=8x,则x=80;
若6x+160<8x,则x>80.
∴当购买数量不足80件时,选择乙超市购买;
当购买数量为80件时,两超市支付的费用相同;
当购买数量超过 80件时,选择甲超市购买.
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费: 35元/次;
白金卡消费: 购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费: 购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
35 × 6=210
<280
<560
解:(1)
李叔叔应选择普通消费方式更合算.
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(2)
普通消费:
y=35x
白金卡消费:
35(x-12)+ 280
=35x-140
y=
(x≤12)
280
(x>12)
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
(3)当x=18时,y普通=35×18=630;
y白金卡=35×18-140=490;
令y白金卡=560,即35x-140=560,
解得:x=20.
当18≤x≤19时,选择白金卡消费最合算;
当x=20时,选择白金卡消费和钻石卡消费费用相同;
当x≥21时,选择钻石卡消费最合算.
5.某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车.在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱材料;若租用20辆甲型货车和60辆乙型货车可装载1400箱材料.
(1)甲、乙两种型号的货车每辆分别可装载多少箱材料
(2)经初步估算,公司要运往工厂的这批材料不超过1245箱计划租用甲、乙两种型号的货车共 70辆,且乙型货车的数量不超过甲型货车数量的3倍,该公司一次性将这批材料运往工厂共有哪几种租车方案
答:甲型货车每辆可装载 25 箱材料,乙型货车每辆可装载15箱材料.
30x+50y=1500,
20x+60y=1400.
x=25,
y=15.
5.某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车.在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱材料;若租用20辆甲型货车和60辆乙型货车可装载1400箱材料.
(1)甲、乙两种型号的货车每辆分别可装载多少箱材料
(1)设甲型货车每辆可装载x箱材料,乙型货车
每辆可装载 y箱材料.根据题意,得
解:
∴
(2)设租用m辆甲型货车,则租用(70-m)辆乙型货车.
根据题意,得
∵ m为整数, ∴ m可以取18,19.
∴该公司共有2种租车方案.
方案一:租用18辆甲型货车,52辆乙型货车;
方案二:租用19辆甲型货车,51辆乙型货车.
25m+15(70-m)≤1245,
70-m≤3m,
∴ ≤m≤ ,
m≤
∴
39
2
-
m≥
35
2
-
35
2
-
39
2
-
第12章 一次函数 期末复习 (6)
方案选择问题
某学校计划在总费用2 300 元的限额内,租用汽车
送234 名学生和6 名教师集体外出活动,每辆汽车上至
少要有1 名教师.现在有甲、乙两种大客车,它们的载
客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
典型例析
问题1 影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
问题2 所租汽车辆数又与哪些因素有关?
与乘车人数有关.
问题3 如何由乘车人数确定租车辆数呢?
(2)要使每辆汽车上至少有1 名教师,汽车
总数不能大于 .
问题3 如何由乘车人数确定租车辆数呢?
(1)要保证240 名师生都有车坐,汽车
总数不能小于 ;
6 辆
6 辆
∴汽车总数为 .
6 辆
问题4 在汽车总数确定后,租车费用与租车的种类有关.如果租甲类车x 辆,能求出租车费用吗?
设租用 x 辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;
设租车费用为 y,
则
y =
400x
化简 得
y =
+
280(6-x)
120x+1 680.
k =
120
∴y 随着 x 的增大而增大,
> 0,
∴当甲类车取最少时,
租车费用y 为最少.
(1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
问题5 如何确定 y =120x+1 680中 y 的最小值.
45x+30(6-x)≥240
400x+280(6-x)≤2 300
由
得 4≤x≤ .
31
6
据实际意义可取4 或5;
∴当 x =4 时,
∵ y 随着 x 的增大而增大,
y 的最小值为2 160.
y 最小,
解:设租用x 辆甲种客车,则租用乙种客车的辆数
为(6-x)辆;设租车费用为 y,则
y =400x+280(6-x)
化简 得y =120x+1 680.
(1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
45x+30(6-x)≥240
400x+280(6-x)≤2 300
由
得 4≤x≤ .
据实际意义可取4 或5;
∵ y 随着 x 的增大而增大, ∴当 x =4 时,
y 最小,y 的最小值为2 160.
31
6
1.某中学为增强学生体质,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需510元;购买3个篮球和5个足球共需810元.
(1)求篮球和足球的单价分别是多少元.
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元,那么有哪几种购买方案
练习巩固
方案设计问题
解:(1)设篮球的单价为a元,足球的单价为b元.
根据题意,得
答:篮球的单价为120元,足球的单价为90元.
3a+5b=810.
2a+3b=510,
a=120,
b=90.
∴
(2)设采购篮球x个,则采购足球(50-x)个.
∵要求篮球不少于30个,且总费用不超过5500元,
∵ x为整数, ∴ x的值可为30,31,32,33.
因此共有四种购买方案.
方案一:采购篮球 30个,采购足球20个;
方案二:采购篮球31个, 采购足球19个;
方案三:采购篮球 32个,采购足球 18个;
方案四:采购篮球 33个,采购足球 17 个.
120x+90(50-x)≤5500
x≥30,
∴
∴
30≤x≤
100
3
-
2. 某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
2. 某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
解:(1)设 A、B 两种型号电动自行车的进货单价分别为 x 元、 (x+500)元.由题意:
解得 x=2500,
经检验:x=2500 是分式方程的解.
答:A、B 两种型号电动自行车的进货单价分别为 2500 元 ,3000 元.
x+500
50000
x
60000
=
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(2)y=300m+500(30-m)
=-200m+15000 (20≤m≤30),
(3)该商店如何进货才能获得最大利润?此时最大利润
是多少元?
(3)∵y=300m+500(30-m)
=-200m+15000,
∵k=-200<0,
∴ y随m的增大而减小,
∵ 20≤m≤30,
∴m=20 时,y 有最大值,最大值为 11000 元.
3.某单位准备购买文化用品,该文化用品在甲、乙两家超市的标价均为10元/件现甲、乙两家超市进行促销活动.
甲超市:一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖.
乙超市:全部按标价的8折售卖.
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为___元,在乙超市的购物金额为 元.
(2)假如你是该单位的采购员,为使支付的费用较少,你应该选择哪家超市购买
2.某单位准备购买文化用品,该文化用品在甲、乙两家超市的标价均为10元/件现甲、乙两家超市进行促销活动.
甲超市:一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖.
乙超市:全部按标价的8折售卖.
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为___ 元,在乙超市的购物金额为 元.
300
240
(2)设购买x件这种文化用品.
①当0
在乙超市的购物金额为0.8×10x=8x(元),
∵ 10x>8x,所以选择乙超市购买.
②当x>40时,
在甲超市的购物金额为
400+0.6×(10x-400)=(6x +160)(元),
在乙超市的购物金额为
0.8×10x=8x(元)
若6x+160>8x,则40
若6x+160<8x,则x>80.
∴当购买数量不足80件时,选择乙超市购买;
当购买数量为80件时,两超市支付的费用相同;
当购买数量超过 80件时,选择甲超市购买.
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费: 35元/次;
白金卡消费: 购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费: 购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
35 × 6=210
<280
<560
解:(1)
李叔叔应选择普通消费方式更合算.
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(2)
普通消费:
y=35x
白金卡消费:
35(x-12)+ 280
=35x-140
y=
(x≤12)
280
(x>12)
4.为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
(3)当x=18时,y普通=35×18=630;
y白金卡=35×18-140=490;
令y白金卡=560,即35x-140=560,
解得:x=20.
当18≤x≤19时,选择白金卡消费最合算;
当x=20时,选择白金卡消费和钻石卡消费费用相同;
当x≥21时,选择钻石卡消费最合算.
5.某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车.在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱材料;若租用20辆甲型货车和60辆乙型货车可装载1400箱材料.
(1)甲、乙两种型号的货车每辆分别可装载多少箱材料
(2)经初步估算,公司要运往工厂的这批材料不超过1245箱计划租用甲、乙两种型号的货车共 70辆,且乙型货车的数量不超过甲型货车数量的3倍,该公司一次性将这批材料运往工厂共有哪几种租车方案
答:甲型货车每辆可装载 25 箱材料,乙型货车每辆可装载15箱材料.
30x+50y=1500,
20x+60y=1400.
x=25,
y=15.
5.某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车.在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱材料;若租用20辆甲型货车和60辆乙型货车可装载1400箱材料.
(1)甲、乙两种型号的货车每辆分别可装载多少箱材料
(1)设甲型货车每辆可装载x箱材料,乙型货车
每辆可装载 y箱材料.根据题意,得
解:
∴
(2)设租用m辆甲型货车,则租用(70-m)辆乙型货车.
根据题意,得
∵ m为整数, ∴ m可以取18,19.
∴该公司共有2种租车方案.
方案一:租用18辆甲型货车,52辆乙型货车;
方案二:租用19辆甲型货车,51辆乙型货车.
25m+15(70-m)≤1245,
70-m≤3m,
∴ ≤m≤ ,
m≤
∴
39
2
-
m≥
35
2
-
35
2
-
39
2
-
