第12章一次函数期末复习(7)一次函数的最值问题 课件(共21张PPT)
文档属性
| 名称 | 第12章一次函数期末复习(7)一次函数的最值问题 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 121.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第12章 一次函数 期末复习 (7)
一次函数的最值问题
(1)用一次函数的图象寻求实际问题中的变化规律解题.
(2)利用两个一次函数的图象解决方案选择问题.
用一次函数解决实际问题
常考角度
1.分段函数问题(分段价格、几何动点)由形求式
(单个函数图象、多个函数图象)
2.方案设计问题(物资调运、方案比较).
3.一次函数最值问题.
复习要点
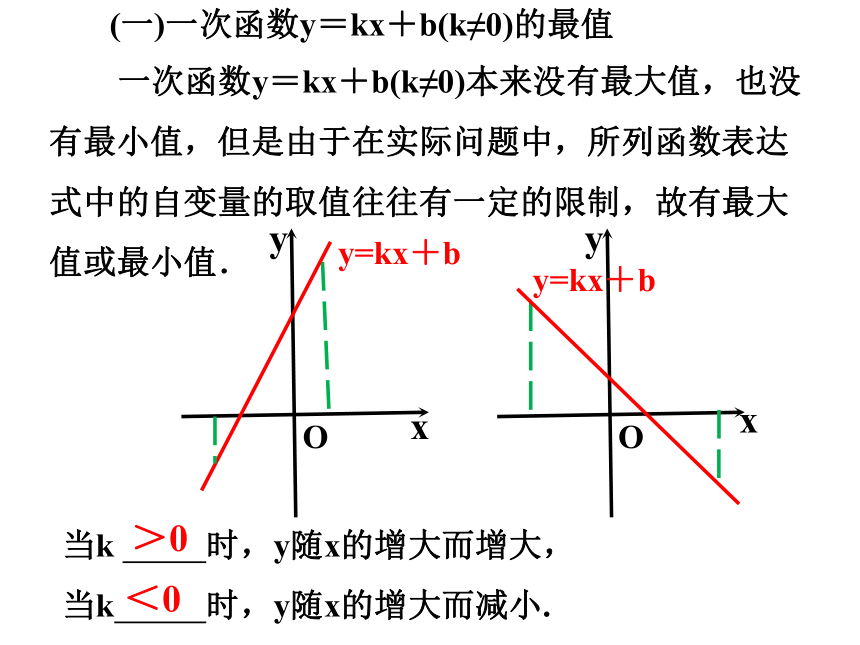
一次函数y=kx+b(k≠0)本来没有最大值,也没有最小值,但是由于在实际问题中,所列函数表达式中的自变量的取值往往有一定的限制,故有最大值或最小值.
(一)一次函数y=kx+b(k≠0)的最值
当k 时,y随x的增大而增大,
当k 时,y随x的增大而减小.
>0
<0
x
y
O
y=kx+b
x
y
O
y=kx+b
例1 我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
典型例析
一次函数最值问题.
解:(1)设甲商品购进x件,则乙商品购进(100-x)件,
由题意,得
y=
∴y与x之间的函数关系式为:
例1我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
y=-5x+1 000.
(20-15)x
+(45-35)(100-x)
=-5x+1 000,
(2)由题意,得
解得 x≥25.
∵y=-5x+1 000,k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y取最大值,
此时y=-5×25+1 000=875(元),
∴至少要购进25件甲种商品;
若售完这些商品,商家可获得的最大利润是875 元.
15x+35(100-x)≤3 000,
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
例2 我市某校购买三角梅5盆和绣球花3盆, 需要210元;购买三角梅3盆和绣球花5盆, 需要190元.
(1)求学校购买三角梅、绣球花每盆各需多少钱?
(2) 考虑到绿化效果和资金周转, 学校计划购买两种盆栽共100盆,且购买三角梅的盆数不少于绣球花的盆数的2倍,设购买三角梅a盆, 所需资金为w元.
①请求w与a的函数关系式;
②怎样购买所需资金最少?
典型例析
5x+3y=210
3x+5y=190
x=30
y=20 .
解得,
我市某校购买三角梅5盆和绣球花3盆, 需要210元;购买三角梅3盆和绣球花5盆, 需要190元.
(1)求学校购买三角梅、绣球花每盆各需多少钱?
解: (1)设三角梅每盆x元,绣球花每盆y元,
依题意,得
答:学校购买三角梅每盆30元,绣球花每盆20元.
(2) 考虑到绿化效果和资金周转, 学校计划购买两种盆栽共100盆,且购买三角梅的盆数不少于绣球花的盆数的2倍,设购买三角梅a盆, 所需资金为w元.
①请求w与a的函数关系式;
(2) ① ∵购买两种盆栽共100盆,三角梅为a盆,
∴购买绣球花为(100 - a)盆,
∴ W=30a+20(100-a)
=10a+2000
(2) 考虑到绿化效果和资金周转, 学校计划购买两种盆栽共100盆,且购买三角梅的盆数不少于绣球花的盆数的2倍,设购买三角梅a盆, 所需资金为w元. ②怎样购买所需资金最少?
(2) ② ∵三角梅的盆数不少于绣球花的盆数的2倍,
∴ a≥2(100-a),
又∵ a≤100,且a为整数,
∴ ≤a≤100,且a为整数.
∵ k=10>0, ∴ W随a的增大而增大.
∴当a=67时,W取得最小值,
此时,100-a=100-67=33盆.
答:学校购买67盆三角梅和33盆绣球花时,所需资金最小.
200
3
-
200
3
-
∴ a≥
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
练习巩固
解:(1)设甲商品购进x件,则乙商品购进(100-x)件,
由题意,得
y=
∴y与x之间的函数关系式为:
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
y=-5x+1 000.
(20-15)x
+(45-35)(100-x)
=-5x+1 000,
练习巩固
(2)由题意,得
解得 x≥25.
∵y=-5x+1 000,k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y取最大值,
此时y=-5×25+1 000=875(元),
∴至少要购进25件甲种商品;
若售完这些商品,商家可获得的最大利润是875 元.
15x+35(100-x)≤3 000,
A店有肥料200t
B店有肥料300t
C村需要肥料240t
D村需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
2.A店有肥料200t,B店有肥料300t,现要把这些肥料
全部运往C,D两村.从A店运往C,D两村运肥料的费用分
别为20元/t和25元/t;从B店运往C,D两村运肥料的费用
分别是15元/t和24元/t.现C村需要肥料240t,D村需要肥料
260t,怎样调运可是总运费最少?
A店有肥料200t
B店有肥料300t
C村需要肥料240t
D村需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
运费
2.A店有肥料200t,B店有肥料300t,现要把这些肥料
全部运往C,D两村.从A店运往C,D两村运肥料的费用分
别为20元/t和25元/t;从B店运往C,D两村运肥料的费用
分别是15元/t和24元/t.现C村需要肥料240t,D村需要肥料
260t,怎样调运可是总运费最少?
A店有肥料200t
B店有肥料300t
C村需要肥料240t
D村需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A店运肥料xt到C村,总运费为y元,则有
y=
整理,得
y=
4x
+10040
(0≤x≤200)
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A店运肥料xt到C村,总运费为y元,则有
y=
整理,得
y=
4x
+10040
∵k=4>0,
∴y随x的增大而增大,
(0≤x≤200)
∴x最小时y最小.
∵x最小值为0,
∴从A店运到C村肥料为0t.
即A店200t肥料全运往D村,
再从B店的运60t肥料往D村,
C村所需要的240t肥料全从B店运,
可使总运费最少.
3.某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为2400元和4000元.
(1)设招聘甲种工种工人x人,工厂付给甲、乙两种工种的工人工资共y元,写出y(元)与x(人)的函数关系式;
(2)现要求招聘的乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
3.某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为2400元和4000元. (1)设招聘甲种工种工人x人,工厂付给甲、乙两种工种的工人工资共y元,写出y(元)与x(人)的函数关系式;
∵招聘甲种工种工人x人,
∴ y =
2400x
化简 得
y =
4000(150-x)
-1600x+600000.
解:(1)
∴招聘乙种工种工人为(150-x)人,
+
1.某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为2400元和4000元.
(2)现要求招聘的乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
解:(2)
∵招聘的乙种工种的人数不少于甲种工
种人数的2倍,
∴ 150-x ≥ 2x,
∴x ≤ 50.
∴x最大时y最小.
∵k=-1600<0,
∴y随x的增大而减小,
解:(2)
∵招聘的乙种工种的人数不少于甲种工
种人数的2倍,
∴ 150-x ≥ 2x,
∴ 0≤x≤50.
答: 甲工种招聘50人,乙工种招聘100人时
可使得每月所付的工资最少.
∵k=-1600<0,
∴150-50=100
∴y随x的增大而减小,
∴当x=50时,y有最小值.
第12章 一次函数 期末复习 (7)
一次函数的最值问题
(1)用一次函数的图象寻求实际问题中的变化规律解题.
(2)利用两个一次函数的图象解决方案选择问题.
用一次函数解决实际问题
常考角度
1.分段函数问题(分段价格、几何动点)由形求式
(单个函数图象、多个函数图象)
2.方案设计问题(物资调运、方案比较).
3.一次函数最值问题.
复习要点
一次函数y=kx+b(k≠0)本来没有最大值,也没有最小值,但是由于在实际问题中,所列函数表达式中的自变量的取值往往有一定的限制,故有最大值或最小值.
(一)一次函数y=kx+b(k≠0)的最值
当k 时,y随x的增大而增大,
当k 时,y随x的增大而减小.
>0
<0
x
y
O
y=kx+b
x
y
O
y=kx+b
例1 我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
典型例析
一次函数最值问题.
解:(1)设甲商品购进x件,则乙商品购进(100-x)件,
由题意,得
y=
∴y与x之间的函数关系式为:
例1我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
y=-5x+1 000.
(20-15)x
+(45-35)(100-x)
=-5x+1 000,
(2)由题意,得
解得 x≥25.
∵y=-5x+1 000,k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y取最大值,
此时y=-5×25+1 000=875(元),
∴至少要购进25件甲种商品;
若售完这些商品,商家可获得的最大利润是875 元.
15x+35(100-x)≤3 000,
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
例2 我市某校购买三角梅5盆和绣球花3盆, 需要210元;购买三角梅3盆和绣球花5盆, 需要190元.
(1)求学校购买三角梅、绣球花每盆各需多少钱?
(2) 考虑到绿化效果和资金周转, 学校计划购买两种盆栽共100盆,且购买三角梅的盆数不少于绣球花的盆数的2倍,设购买三角梅a盆, 所需资金为w元.
①请求w与a的函数关系式;
②怎样购买所需资金最少?
典型例析
5x+3y=210
3x+5y=190
x=30
y=20 .
解得,
我市某校购买三角梅5盆和绣球花3盆, 需要210元;购买三角梅3盆和绣球花5盆, 需要190元.
(1)求学校购买三角梅、绣球花每盆各需多少钱?
解: (1)设三角梅每盆x元,绣球花每盆y元,
依题意,得
答:学校购买三角梅每盆30元,绣球花每盆20元.
(2) 考虑到绿化效果和资金周转, 学校计划购买两种盆栽共100盆,且购买三角梅的盆数不少于绣球花的盆数的2倍,设购买三角梅a盆, 所需资金为w元.
①请求w与a的函数关系式;
(2) ① ∵购买两种盆栽共100盆,三角梅为a盆,
∴购买绣球花为(100 - a)盆,
∴ W=30a+20(100-a)
=10a+2000
(2) 考虑到绿化效果和资金周转, 学校计划购买两种盆栽共100盆,且购买三角梅的盆数不少于绣球花的盆数的2倍,设购买三角梅a盆, 所需资金为w元. ②怎样购买所需资金最少?
(2) ② ∵三角梅的盆数不少于绣球花的盆数的2倍,
∴ a≥2(100-a),
又∵ a≤100,且a为整数,
∴ ≤a≤100,且a为整数.
∵ k=10>0, ∴ W随a的增大而增大.
∴当a=67时,W取得最小值,
此时,100-a=100-67=33盆.
答:学校购买67盆三角梅和33盆绣球花时,所需资金最小.
200
3
-
200
3
-
∴ a≥
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
练习巩固
解:(1)设甲商品购进x件,则乙商品购进(100-x)件,
由题意,得
y=
∴y与x之间的函数关系式为:
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
y=-5x+1 000.
(20-15)x
+(45-35)(100-x)
=-5x+1 000,
练习巩固
(2)由题意,得
解得 x≥25.
∵y=-5x+1 000,k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y取最大值,
此时y=-5×25+1 000=875(元),
∴至少要购进25件甲种商品;
若售完这些商品,商家可获得的最大利润是875 元.
15x+35(100-x)≤3 000,
A店有肥料200t
B店有肥料300t
C村需要肥料240t
D村需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
2.A店有肥料200t,B店有肥料300t,现要把这些肥料
全部运往C,D两村.从A店运往C,D两村运肥料的费用分
别为20元/t和25元/t;从B店运往C,D两村运肥料的费用
分别是15元/t和24元/t.现C村需要肥料240t,D村需要肥料
260t,怎样调运可是总运费最少?
A店有肥料200t
B店有肥料300t
C村需要肥料240t
D村需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
运费
2.A店有肥料200t,B店有肥料300t,现要把这些肥料
全部运往C,D两村.从A店运往C,D两村运肥料的费用分
别为20元/t和25元/t;从B店运往C,D两村运肥料的费用
分别是15元/t和24元/t.现C村需要肥料240t,D村需要肥料
260t,怎样调运可是总运费最少?
A店有肥料200t
B店有肥料300t
C村需要肥料240t
D村需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A店运肥料xt到C村,总运费为y元,则有
y=
整理,得
y=
4x
+10040
(0≤x≤200)
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A店运肥料xt到C村,总运费为y元,则有
y=
整理,得
y=
4x
+10040
∵k=4>0,
∴y随x的增大而增大,
(0≤x≤200)
∴x最小时y最小.
∵x最小值为0,
∴从A店运到C村肥料为0t.
即A店200t肥料全运往D村,
再从B店的运60t肥料往D村,
C村所需要的240t肥料全从B店运,
可使总运费最少.
3.某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为2400元和4000元.
(1)设招聘甲种工种工人x人,工厂付给甲、乙两种工种的工人工资共y元,写出y(元)与x(人)的函数关系式;
(2)现要求招聘的乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
3.某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为2400元和4000元. (1)设招聘甲种工种工人x人,工厂付给甲、乙两种工种的工人工资共y元,写出y(元)与x(人)的函数关系式;
∵招聘甲种工种工人x人,
∴ y =
2400x
化简 得
y =
4000(150-x)
-1600x+600000.
解:(1)
∴招聘乙种工种工人为(150-x)人,
+
1.某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为2400元和4000元.
(2)现要求招聘的乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
解:(2)
∵招聘的乙种工种的人数不少于甲种工
种人数的2倍,
∴ 150-x ≥ 2x,
∴x ≤ 50.
∴x最大时y最小.
∵k=-1600<0,
∴y随x的增大而减小,
解:(2)
∵招聘的乙种工种的人数不少于甲种工
种人数的2倍,
∴ 150-x ≥ 2x,
∴ 0≤x≤50.
答: 甲工种招聘50人,乙工种招聘100人时
可使得每月所付的工资最少.
∵k=-1600<0,
∴150-50=100
∴y随x的增大而减小,
∴当x=50时,y有最小值.
