第12章一次函数期末复习(3)一次函数与图形面积 课件(共22张PPT)
文档属性
| 名称 | 第12章一次函数期末复习(3)一次函数与图形面积 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 155.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 23:32:03 | ||
图片预览




文档简介
(共22张PPT)
第12章 一次函数 期末复习 (3)
一次函数与图形面积
复习要点
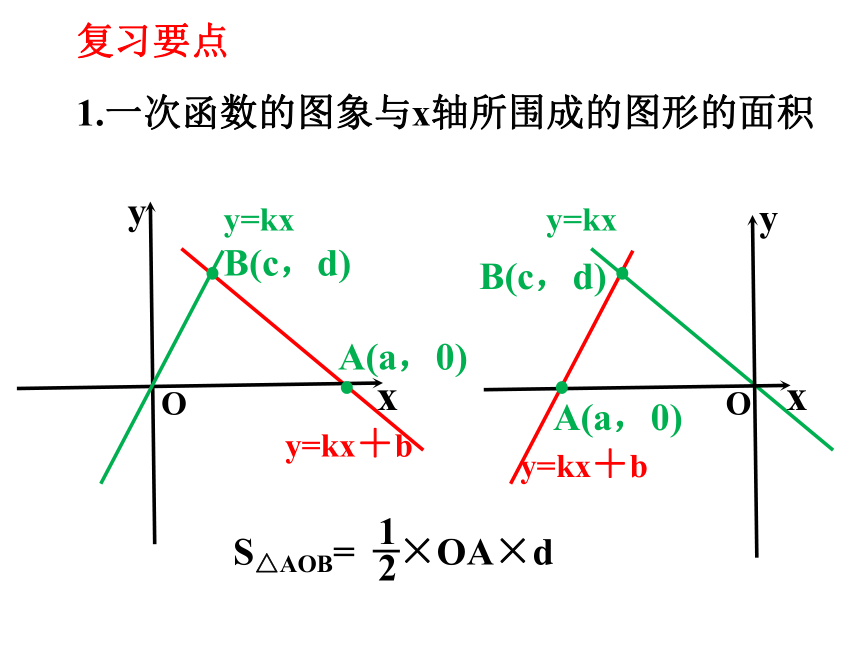
1.一次函数的图象与x轴所围成的图形的面积
y=kx+b
x
y
O
y=kx
B(c,d)
A(a,0)
y=kx+b
x
y
O
y=kx
B(c,d)
A(a,0)
S△AOB=
×OA×d
1
2
复习要点
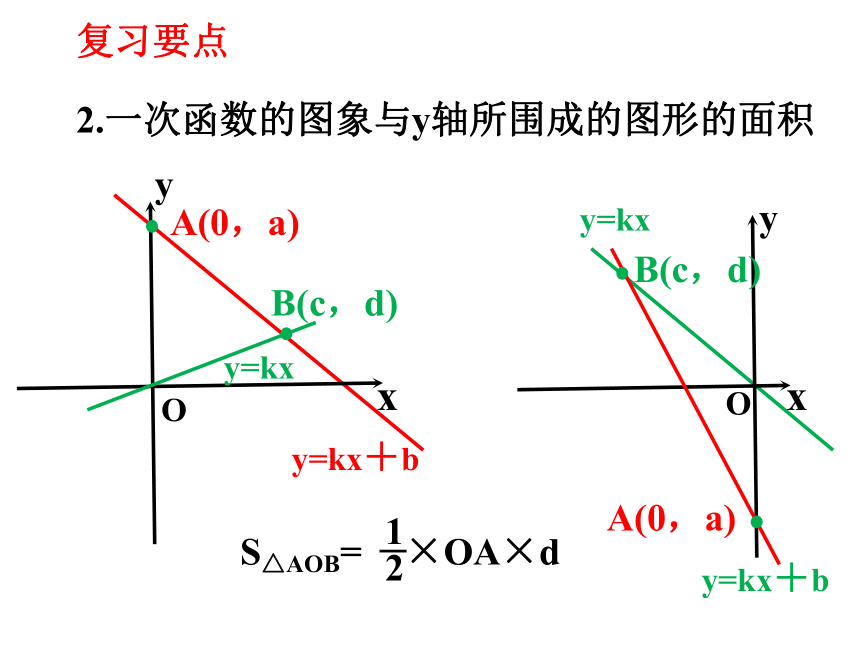
2.一次函数的图象与y轴所围成的图形的面积
y=kx+b
x
y
O
y=kx
B(c,d)
A(0,a)
y=kx+b
x
y
O
y=kx
B(c,d)
A(0,a)
S△AOB=
×OA×d
1
2
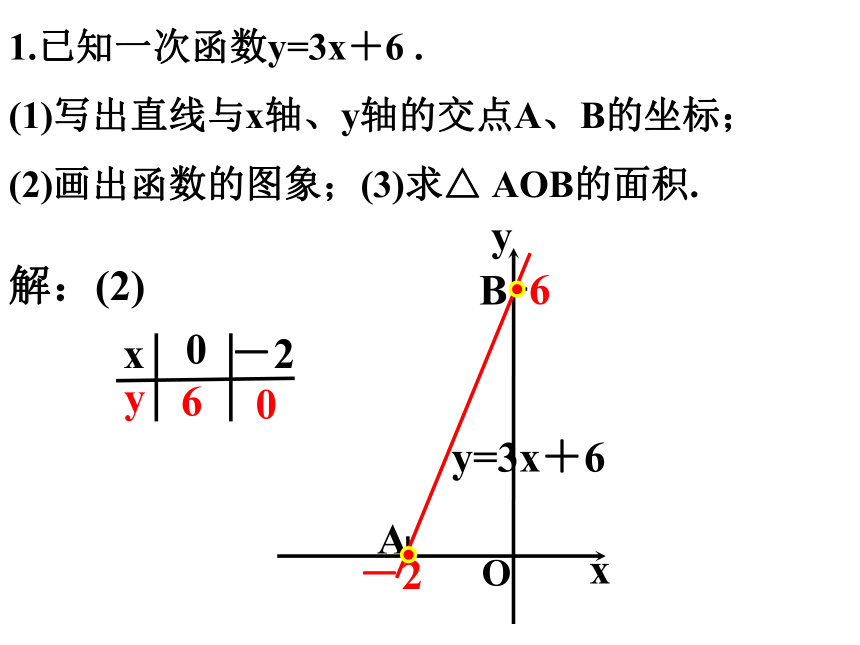
1.已知一次函数y=3x+6 .
(1)写出直线与x轴、y轴的交点A、B的坐标;
(2)画出函数的图象;(3)求△ AOB的面积.
解:(1)
∵点A在x轴上,
∴点A的纵坐标为0,
∴3x+6=0,
∴x=-2,
∴点A的坐标为(-2,0);
∵点B在y轴上,
∴点B的横坐标为0,
∴y=3×0+6
∴点B的坐标为(0,6).
=6
典型例析
1.已知一次函数y=3x+6 .
(1)写出直线与x轴、y轴的交点A、B的坐标;
(2)画出函数的图象;(3)求△ AOB的面积.
x
y
O
6
-2
解:(2)
A
B
y=3x+6
y
x
0
6
-2
0
1.已知一次函数y=3x+6 .
(1)写出直线与x轴、y轴的交点A、B的坐标;
(2)画出函数的图象;(3)求△ AOB的面积.
x
y
O
6
-2
解:(3)
∵A(-2,0),
B(0,6).
A
B
y=3x+6
∴S△AOB
=
OA
×OB
1
2
=
1
2
×2
×6
=6.
∴OA=2,
OB=6,
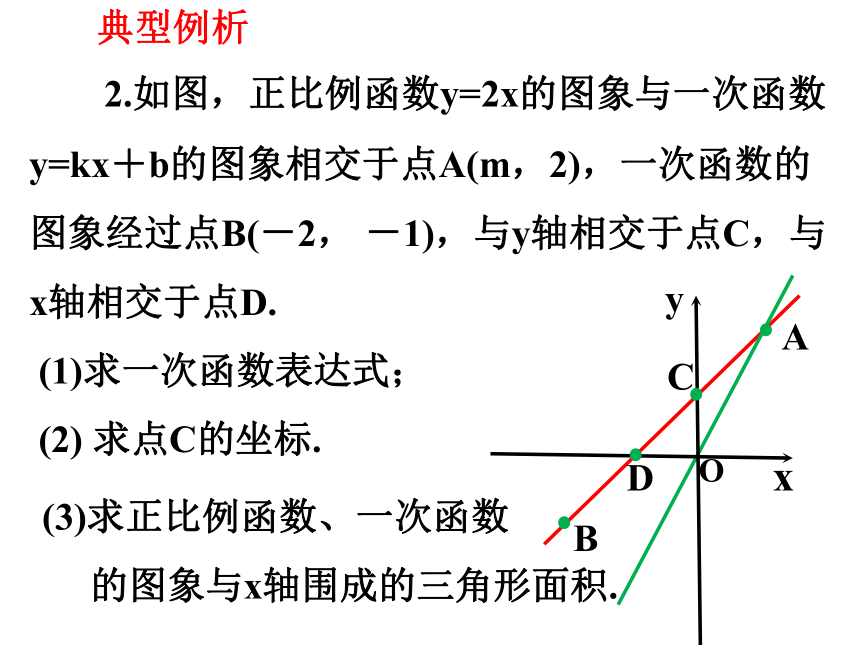
2.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象相交于点A(m,2),一次函数的图象经过点B(-2, -1),与y轴相交于点C,与x轴相交于点D.
(1)求一次函数表达式;
(2) 求点C的坐标.
典型例析
(3)求正比例函数、一次函数
的图象与x轴围成的三角形面积.
x
y
O
A
B
C
D
2.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象相交于点A(m,2),一次函数的图象经过点B(-2, -1),与y轴相交于点C,与x轴相交于点D. (1)求一次函数表达式;
解:(1)
∵点A(m,2)正比例函数y=2x的图象上,
∴ 2=2m,
∴ m=1.
∴点A的坐标为(1,2)
∵一次函数的图象经过点A,B,
x
y
O
A
B
C
D
k+b =2
-2k+b =-1
∴
k=1
b=1
∴
∴一次函数表达式为
y=x+1
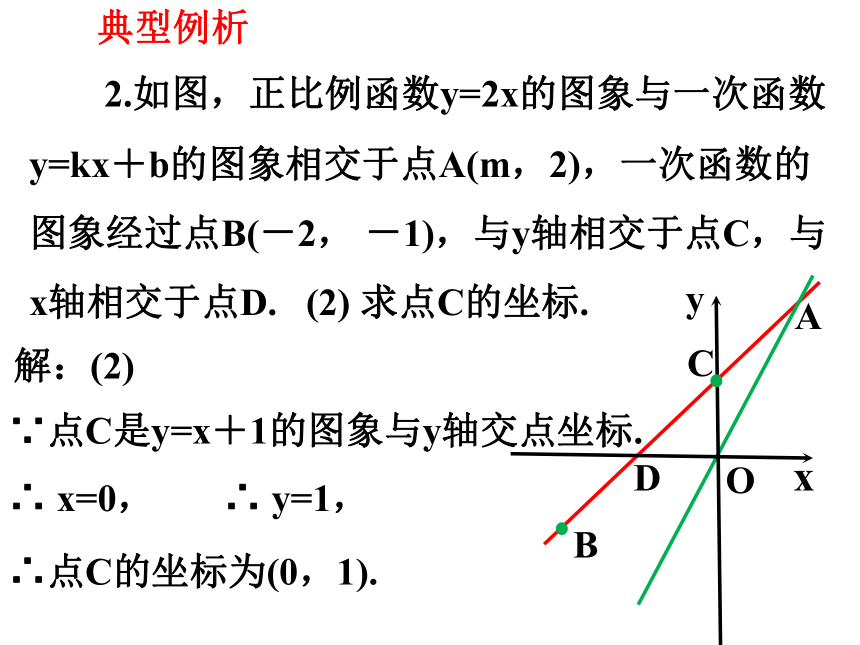
2.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象相交于点A(m,2),一次函数的图象经过点B(-2, -1),与y轴相交于点C,与x轴相交于点D. (2) 求点C的坐标.
典型例析
∵点C是y=x+1的图象与y轴交点坐标.
解:(2)
∴ x=0,
∴点C的坐标为(0,1).
∴ y=1,
x
y
O
A
B
C
D
(3)求正比例函数、一次函数的图象与x轴围成的三角形面积.
解:(3)
x
y
O
A
B
C
D
∵点D是y=x+1的图象与x轴交点坐标.
∴ y=0,
∴点D的坐标为(-1,0).
∴ x=-1.
∴OD=1.
∵点A的坐标为(1,2),
∴ x+1=0,
∴ △AOD中OD边上的高为2.
∴ S△AOD=
×OD×2
=
×1×2
=1
1
2
1
2
1.函数y=2x-8的图象与坐标轴所围成的图形的
面积是____.
16
练习巩固
解:当x=0时, y=2x-8= -8,
∴直线y=2x-8与y轴交于A(0,-8);
当y=0时,即2x-8=0,∴x=4,
∴直线y=2x-8与x轴交于B(4,0);
∴S△AOB= OA×OB= ×4×8=16.
y=2x-8
x
y
O
A
B
2.已知y=-2x+6,则该直线与坐标轴所围成的
三角形的面积是_____.
点B的坐标为(0,6),
∴点A的坐标为(3,0) ,
∴S△AOB
=
OA
×OB
1
2
=
1
2
×3
×6
=9.
∴OA=3,
∴OB=6,
9
设-2x+6 =0,
则x=3,
设x=0,
则y=6,
x
O
y
y=-2x+6
A
B
3.在同一平面直角坐标系中,直线y=2x与 y=-2x+8相交于点A,直线y=-2x+8与x轴交于点B,则△ AOB的面积为 .
4
4.在平面直角坐标系中,直线y=kx+3与坐标轴所围成的三角形的面积是3,则k的值为( ).
A.- B. C. D.2
3
2
3
2
3
2
2或-
或-
3
2
B
5.已知直线y=kx+b与直线 y= x+3交点的纵坐标为5,而与直线y=3x-9的交点的横坐标也是5,则直线y=kx+b与两坐标轴围成的三角形面积为( ).
1
2
A. B. C. D.1
1
2
3
2
5
2
A
(4,5)
(5,6)
y=kx+b
y=x+1
S△=
×1×1
1
2
6. 直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk,当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200
=( ).
A. 10000 B. 10050
C. 10100 D 10150
B
7.已知一次函数y= x+m与y=- x+n的图象都经过点A(-2, 3),且与y轴分别相交于B,C两点.求△ ABC的面积.
3
2
1
2
解:
∵一次函数y= x+m的图象经过点A(-2, 3),
3
2
∴ ×(-2)+m=3,
3
2
∴ m=6.
∴点B的坐标(0,6).
∵一次函数y=- x+n的图象经过点A(-2, 3),
1
2
∴ - ×(-2)+n=3,
1
2
∴ n=2.
∴点C的坐标(0,2).
∴BC= m-n=6-2=4.
∴ S△ABC=
×BC×2
1
2
=BC=4.
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(1)求直线n的解析式;
(2)求△ADC的面积
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(1)求直线n的解析式;
y=-3x+3
x
O
y
B
C
A
D
解:(1)
∴
4k+b=0
3k+b=-1.5
∴n的解析式为
y=1.5x-6
∵ n经过点B,点C
∴
k=1.5
b=-6
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(1)求直线n的解析式;
(2)求△ADC的面积
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
SΔADC
=
SΔADB
-SΔABC
AB
AB的高
D的纵坐标
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(2)求△ADC的面积.
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
设-3x+3=0
则x=1
∴ OA=1
设1.5x-6=0
则x=4
∴ OB=4
∴ AB=OB-OA
=4-1
=3
(2)
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
设-3x+3=0
则x=1
∴ OA=1
设1.5x-6=0
则x=4
∴ OB=4
∴ AB=OB-OA
=4-1
=3
(2)
∵
y=-3x+3
y=1.5x-6
∴
x=2
y=-3
∴点D的坐标为(2,-3)
∴SΔADC
=SΔADB
-SΔABC
=
1
2
×3
×3
-
1
2
×3
×1.5
=
9
4
第12章 一次函数 期末复习 (3)
一次函数与图形面积
复习要点
1.一次函数的图象与x轴所围成的图形的面积
y=kx+b
x
y
O
y=kx
B(c,d)
A(a,0)
y=kx+b
x
y
O
y=kx
B(c,d)
A(a,0)
S△AOB=
×OA×d
1
2
复习要点
2.一次函数的图象与y轴所围成的图形的面积
y=kx+b
x
y
O
y=kx
B(c,d)
A(0,a)
y=kx+b
x
y
O
y=kx
B(c,d)
A(0,a)
S△AOB=
×OA×d
1
2
1.已知一次函数y=3x+6 .
(1)写出直线与x轴、y轴的交点A、B的坐标;
(2)画出函数的图象;(3)求△ AOB的面积.
解:(1)
∵点A在x轴上,
∴点A的纵坐标为0,
∴3x+6=0,
∴x=-2,
∴点A的坐标为(-2,0);
∵点B在y轴上,
∴点B的横坐标为0,
∴y=3×0+6
∴点B的坐标为(0,6).
=6
典型例析
1.已知一次函数y=3x+6 .
(1)写出直线与x轴、y轴的交点A、B的坐标;
(2)画出函数的图象;(3)求△ AOB的面积.
x
y
O
6
-2
解:(2)
A
B
y=3x+6
y
x
0
6
-2
0
1.已知一次函数y=3x+6 .
(1)写出直线与x轴、y轴的交点A、B的坐标;
(2)画出函数的图象;(3)求△ AOB的面积.
x
y
O
6
-2
解:(3)
∵A(-2,0),
B(0,6).
A
B
y=3x+6
∴S△AOB
=
OA
×OB
1
2
=
1
2
×2
×6
=6.
∴OA=2,
OB=6,
2.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象相交于点A(m,2),一次函数的图象经过点B(-2, -1),与y轴相交于点C,与x轴相交于点D.
(1)求一次函数表达式;
(2) 求点C的坐标.
典型例析
(3)求正比例函数、一次函数
的图象与x轴围成的三角形面积.
x
y
O
A
B
C
D
2.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象相交于点A(m,2),一次函数的图象经过点B(-2, -1),与y轴相交于点C,与x轴相交于点D. (1)求一次函数表达式;
解:(1)
∵点A(m,2)正比例函数y=2x的图象上,
∴ 2=2m,
∴ m=1.
∴点A的坐标为(1,2)
∵一次函数的图象经过点A,B,
x
y
O
A
B
C
D
k+b =2
-2k+b =-1
∴
k=1
b=1
∴
∴一次函数表达式为
y=x+1
2.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象相交于点A(m,2),一次函数的图象经过点B(-2, -1),与y轴相交于点C,与x轴相交于点D. (2) 求点C的坐标.
典型例析
∵点C是y=x+1的图象与y轴交点坐标.
解:(2)
∴ x=0,
∴点C的坐标为(0,1).
∴ y=1,
x
y
O
A
B
C
D
(3)求正比例函数、一次函数的图象与x轴围成的三角形面积.
解:(3)
x
y
O
A
B
C
D
∵点D是y=x+1的图象与x轴交点坐标.
∴ y=0,
∴点D的坐标为(-1,0).
∴ x=-1.
∴OD=1.
∵点A的坐标为(1,2),
∴ x+1=0,
∴ △AOD中OD边上的高为2.
∴ S△AOD=
×OD×2
=
×1×2
=1
1
2
1
2
1.函数y=2x-8的图象与坐标轴所围成的图形的
面积是____.
16
练习巩固
解:当x=0时, y=2x-8= -8,
∴直线y=2x-8与y轴交于A(0,-8);
当y=0时,即2x-8=0,∴x=4,
∴直线y=2x-8与x轴交于B(4,0);
∴S△AOB= OA×OB= ×4×8=16.
y=2x-8
x
y
O
A
B
2.已知y=-2x+6,则该直线与坐标轴所围成的
三角形的面积是_____.
点B的坐标为(0,6),
∴点A的坐标为(3,0) ,
∴S△AOB
=
OA
×OB
1
2
=
1
2
×3
×6
=9.
∴OA=3,
∴OB=6,
9
设-2x+6 =0,
则x=3,
设x=0,
则y=6,
x
O
y
y=-2x+6
A
B
3.在同一平面直角坐标系中,直线y=2x与 y=-2x+8相交于点A,直线y=-2x+8与x轴交于点B,则△ AOB的面积为 .
4
4.在平面直角坐标系中,直线y=kx+3与坐标轴所围成的三角形的面积是3,则k的值为( ).
A.- B. C. D.2
3
2
3
2
3
2
2或-
或-
3
2
B
5.已知直线y=kx+b与直线 y= x+3交点的纵坐标为5,而与直线y=3x-9的交点的横坐标也是5,则直线y=kx+b与两坐标轴围成的三角形面积为( ).
1
2
A. B. C. D.1
1
2
3
2
5
2
A
(4,5)
(5,6)
y=kx+b
y=x+1
S△=
×1×1
1
2
6. 直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk,当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200
=( ).
A. 10000 B. 10050
C. 10100 D 10150
B
7.已知一次函数y= x+m与y=- x+n的图象都经过点A(-2, 3),且与y轴分别相交于B,C两点.求△ ABC的面积.
3
2
1
2
解:
∵一次函数y= x+m的图象经过点A(-2, 3),
3
2
∴ ×(-2)+m=3,
3
2
∴ m=6.
∴点B的坐标(0,6).
∵一次函数y=- x+n的图象经过点A(-2, 3),
1
2
∴ - ×(-2)+n=3,
1
2
∴ n=2.
∴点C的坐标(0,2).
∴BC= m-n=6-2=4.
∴ S△ABC=
×BC×2
1
2
=BC=4.
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(1)求直线n的解析式;
(2)求△ADC的面积
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(1)求直线n的解析式;
y=-3x+3
x
O
y
B
C
A
D
解:(1)
∴
4k+b=0
3k+b=-1.5
∴n的解析式为
y=1.5x-6
∵ n经过点B,点C
∴
k=1.5
b=-6
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(1)求直线n的解析式;
(2)求△ADC的面积
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
SΔADC
=
SΔADB
-SΔABC
AB
AB的高
D的纵坐标
8.如图,直线m的解析式为y=-3x+3,且与x轴交于点A,直线n经过点B(4,0),C(3, - 1.5),直线m、n交于点D.
(2)求△ADC的面积.
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
设-3x+3=0
则x=1
∴ OA=1
设1.5x-6=0
则x=4
∴ OB=4
∴ AB=OB-OA
=4-1
=3
(2)
x
O
y
B
y=-3x+3
n:y=1.5x-6
C
A
D
设-3x+3=0
则x=1
∴ OA=1
设1.5x-6=0
则x=4
∴ OB=4
∴ AB=OB-OA
=4-1
=3
(2)
∵
y=-3x+3
y=1.5x-6
∴
x=2
y=-3
∴点D的坐标为(2,-3)
∴SΔADC
=SΔADB
-SΔABC
=
1
2
×3
×3
-
1
2
×3
×1.5
=
9
4
