北师大版八年级数学下册课件 1.1.4 等边三角形的判定课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册课件 1.1.4 等边三角形的判定课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:45:05 | ||
图片预览








文档简介
(共21张PPT)
第1章 三角形的证明
1.1 等腰三角形
第4课时 等边三角形的判定
1.等边三角形的判定及特殊直角三角形的特点
2.熟练运用定理解决实际问题
1.等边三角形的判定与含30°锐角的直角三角形的应用
2.熟练运用两个定理
教学目标
重难点
1.上面图片是由哪些图形构成的?
提出问题,导入新课
提出问题,导入新课
2.等腰三角形的判定定理是什么?
3.一个三角形满足什么条件时是等边三角形?一个等腰三角形满足什么条件时是等边三角形?与同伴交流.
导入新课
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1. 三个角都相等的三角形是等边三角形;
2. 有一个角等于 60° 的等腰三角形是等边三角形.
探求新知
A
B
C
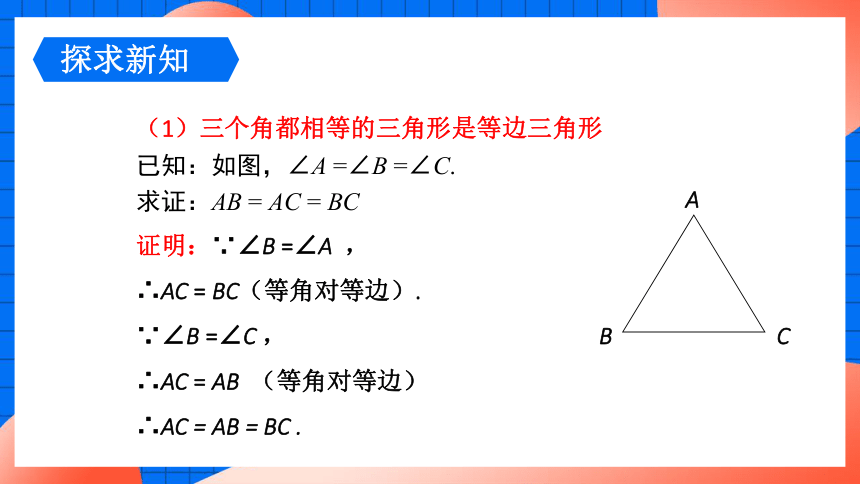
(1)三个角都相等的三角形是等边三角形
已知:如图,∠A =∠B =∠C.
求证:AB = AC = BC
证明:∵∠B =∠A ,
∴AC = BC(等角对等边).
∵∠B =∠C ,
∴AC = AB (等角对等边)
∴AC = AB = BC .
探求新知
(2)有一个角等于60°的等腰三角形是等边三角形.
已知:如图,在△ABC 中, AB=AC,∠B= 60°.
求证: △ABC是等边三角形 .
证明:在△ABC 中, AB=AC,
∴ ∠B= ∠C.
又∵ ∠B = 60° ,∴ ∠C = 60° ,
∴ ∠A = 60° ,∴ ∠A = ∠B.
∴ BC=AC ,
∴ AB=BC=AC ,
∴ △ABC是等边三角形 .
A
B
C
∠A=60°,你能证明吗?
归纳新知
定理 三个角都相等的三角形是等边三角形.
定理 有一个角等于60°的等腰三角形是等边三角形.
等腰三角形(含等边三角形) 性质 判定
等边对等角
等角对等边
“三线合一”,即等腰三角形顶角平分线,底边上的中线、高线互相重合
有一角是 60° 的等腰三角形是等边三角形
等边三角形三个内角都相等,且每个角都是 60°
三个角都相等的三角形是等边三角形
归纳新知
提出问题,探求新知
做一做:用两个含30°角的全等的三角尺,能拼成一个什么三角形吗?与同伴讨论.
等边三角形
提出问题,探求新知
猜想:在直角三角形中,30° 角所对的直角边与斜边有怎样的大小关系?
30°
30°
30° 角所对的直角边是斜边的一半
证明猜想,探求新知
已知:如图在 Rt△ABC 中,∠C = 90°,∠BAC = 30°. 求证:BC = AB.
1
2
A
B
C
证明猜想,探求新知
证明:延长 BC 至 D,使 CD = BC,连接 AD.
∵∠ACB = 90°∴∠ACD = 90°
∵AC = AC,∴△ABC ≌ △ADC(SAS).
∴AB = AD(全等三角形的对应边相等).
∴△ABD 是等边三角形(有一个角是
60°的等腰三角形是等边三角形).
∴BC = BD = AB.
A
B
C
D
1
2
1
2
归纳新知
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:在△ABC 中,
∵∠ACB=90°,∠A=30°.
∴ BC = AB.(在直角三角形中, 30° 角所对的直
角边等于斜边的一半)
A
B
C
30°
巩固练习,提高能力
1. 已知△ABC 中,∠A = ∠B = 60°,AB = 3 cm,则
△ABC 的周长为_____cm.
9
2. 在△ABC 中,∠B = 90°,∠C = 30°,AB = 3,则
AC =_____,BC =______.
A
B
C
3
30°
6
巩固练习,提高能力
3. 房梁的一部分如图所示,其中,BC⊥AC,∠A = 30°,AB = 7.4 m,点 D 是 AB 的中点,且 DE⊥AC,垂足为 E,求 BC,DE 的长.
巩固练习,提高能力
解:在△ABC 中,∠A = 30°,BC⊥AC,
∴BC = AB = 3.7 m.
又∵点 D 是 AB 的中点,
∴AD = BD = 3.7 m,
在△ADE 中,∠A = 30°,DE⊥AC,
∴DE = AD = 1.85 m.
1
2
1
2
巩固练习,提高能力
4.如图,在Rt△ABC 中,∠ACB=90°, ∠B=60°,CD是△ABC 的高,且BD=1,求AD的长.
证明:∵ CD是△ABC 的高,
∴ ∠BDC=90°.
又∵ ∠B=60°,∴∠ BCD= 30°,
∴ BC=2.
∵∠ACB=90°, ∠B=60°,∴∠ A= 30°,
∴ BA=2BC=4.
∴ AD =AB-BD=3.
A
B
C
D
课堂小结
1. 等边三角形的判定:
三个角都相等的三角形是等边三角形.
有一个角是 60° 的等腰三角形是等边三角形.
2. 含 30° 角的直角三角形的性质:
在直角三角形中,如果有一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于 30°.
课后作业
教材第12~13页习题1.4第1,2,3题.
这节课你学到了什么?谈谈你的收获,
小结与反思
第1章 三角形的证明
1.1 等腰三角形
第4课时 等边三角形的判定
1.等边三角形的判定及特殊直角三角形的特点
2.熟练运用定理解决实际问题
1.等边三角形的判定与含30°锐角的直角三角形的应用
2.熟练运用两个定理
教学目标
重难点
1.上面图片是由哪些图形构成的?
提出问题,导入新课
提出问题,导入新课
2.等腰三角形的判定定理是什么?
3.一个三角形满足什么条件时是等边三角形?一个等腰三角形满足什么条件时是等边三角形?与同伴交流.
导入新课
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1. 三个角都相等的三角形是等边三角形;
2. 有一个角等于 60° 的等腰三角形是等边三角形.
探求新知
A
B
C
(1)三个角都相等的三角形是等边三角形
已知:如图,∠A =∠B =∠C.
求证:AB = AC = BC
证明:∵∠B =∠A ,
∴AC = BC(等角对等边).
∵∠B =∠C ,
∴AC = AB (等角对等边)
∴AC = AB = BC .
探求新知
(2)有一个角等于60°的等腰三角形是等边三角形.
已知:如图,在△ABC 中, AB=AC,∠B= 60°.
求证: △ABC是等边三角形 .
证明:在△ABC 中, AB=AC,
∴ ∠B= ∠C.
又∵ ∠B = 60° ,∴ ∠C = 60° ,
∴ ∠A = 60° ,∴ ∠A = ∠B.
∴ BC=AC ,
∴ AB=BC=AC ,
∴ △ABC是等边三角形 .
A
B
C
∠A=60°,你能证明吗?
归纳新知
定理 三个角都相等的三角形是等边三角形.
定理 有一个角等于60°的等腰三角形是等边三角形.
等腰三角形(含等边三角形) 性质 判定
等边对等角
等角对等边
“三线合一”,即等腰三角形顶角平分线,底边上的中线、高线互相重合
有一角是 60° 的等腰三角形是等边三角形
等边三角形三个内角都相等,且每个角都是 60°
三个角都相等的三角形是等边三角形
归纳新知
提出问题,探求新知
做一做:用两个含30°角的全等的三角尺,能拼成一个什么三角形吗?与同伴讨论.
等边三角形
提出问题,探求新知
猜想:在直角三角形中,30° 角所对的直角边与斜边有怎样的大小关系?
30°
30°
30° 角所对的直角边是斜边的一半
证明猜想,探求新知
已知:如图在 Rt△ABC 中,∠C = 90°,∠BAC = 30°. 求证:BC = AB.
1
2
A
B
C
证明猜想,探求新知
证明:延长 BC 至 D,使 CD = BC,连接 AD.
∵∠ACB = 90°∴∠ACD = 90°
∵AC = AC,∴△ABC ≌ △ADC(SAS).
∴AB = AD(全等三角形的对应边相等).
∴△ABD 是等边三角形(有一个角是
60°的等腰三角形是等边三角形).
∴BC = BD = AB.
A
B
C
D
1
2
1
2
归纳新知
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:在△ABC 中,
∵∠ACB=90°,∠A=30°.
∴ BC = AB.(在直角三角形中, 30° 角所对的直
角边等于斜边的一半)
A
B
C
30°
巩固练习,提高能力
1. 已知△ABC 中,∠A = ∠B = 60°,AB = 3 cm,则
△ABC 的周长为_____cm.
9
2. 在△ABC 中,∠B = 90°,∠C = 30°,AB = 3,则
AC =_____,BC =______.
A
B
C
3
30°
6
巩固练习,提高能力
3. 房梁的一部分如图所示,其中,BC⊥AC,∠A = 30°,AB = 7.4 m,点 D 是 AB 的中点,且 DE⊥AC,垂足为 E,求 BC,DE 的长.
巩固练习,提高能力
解:在△ABC 中,∠A = 30°,BC⊥AC,
∴BC = AB = 3.7 m.
又∵点 D 是 AB 的中点,
∴AD = BD = 3.7 m,
在△ADE 中,∠A = 30°,DE⊥AC,
∴DE = AD = 1.85 m.
1
2
1
2
巩固练习,提高能力
4.如图,在Rt△ABC 中,∠ACB=90°, ∠B=60°,CD是△ABC 的高,且BD=1,求AD的长.
证明:∵ CD是△ABC 的高,
∴ ∠BDC=90°.
又∵ ∠B=60°,∴∠ BCD= 30°,
∴ BC=2.
∵∠ACB=90°, ∠B=60°,∴∠ A= 30°,
∴ BA=2BC=4.
∴ AD =AB-BD=3.
A
B
C
D
课堂小结
1. 等边三角形的判定:
三个角都相等的三角形是等边三角形.
有一个角是 60° 的等腰三角形是等边三角形.
2. 含 30° 角的直角三角形的性质:
在直角三角形中,如果有一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于 30°.
课后作业
教材第12~13页习题1.4第1,2,3题.
这节课你学到了什么?谈谈你的收获,
小结与反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
