高三第一轮复习数列一章等差数列与等比数列综合题2
文档属性
| 名称 | 高三第一轮复习数列一章等差数列与等比数列综合题2 |

|
|
| 格式 | rar | ||
| 文件大小 | 50.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-15 00:00:00 | ||
图片预览






文档简介
课件14张PPT。第三章 数 列第2课时 等差、等比数列的通项及
求和公式要点·疑点·考点3.在等差(比)数列中,Sn,S2n-Sn,S3n-S2n,…,Skn-S(k-1)n…成等差(比)数列.其中Sn为前n项的和. 1.等差数列前n项和
等比数列前n项和
2.如果某个数列前n项和为Sn,则2.已知等差数列{an}的前n项和为Sn,若a4=18-a5,则S8等于( )
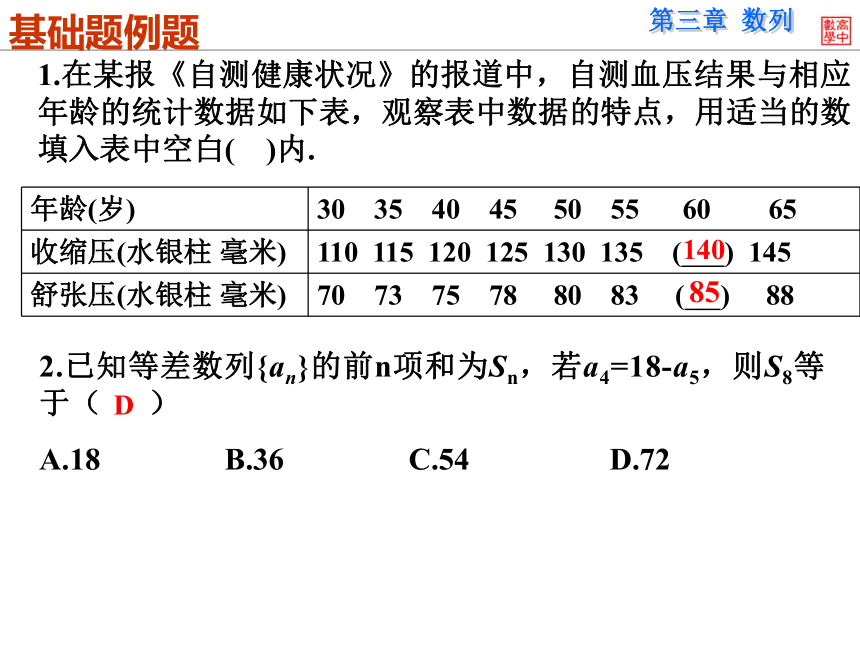
A.18 B.36 C.54 D.72 基础题例题1.在某报《自测健康状况》的报道中,自测血压结果与相应年龄的统计数据如下表,观察表中数据的特点,用适当的数填入表中空白( )内.14085D5.在等差数列{an}中,a2+a4=p,a3+a5=q.则其前6项的
和S6为 ( )
(A) 5 (p+q)/4 (B) 3(p+q)/2 (C) p+q (D) 2(p+q)4.等比数列{an}前n项的乘积为Tn,若Tn=1,T2n=2,则T3n的值为( )
(A)3 (B)4 (C)7 (D)8 DB3.设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q=___1 an=Sn-Sn-1=d (常数)Tn, T2n/Tn, T3n/T2n 也成等比数列基础题例题能力·思维·方法6.设数列{an}的前n项和为Sn=2n2+3n+2,求通项an的表达式,并指出此数列是否为等差数列.解题分析:利用Sn与an的关系,可以求出an.解:n=1时,a1=S1=7,n≥2时,an=Sn-Sn-1=2n2+3n+2-[2(n-1)2+3(n-1)+2]
∴an=4n+1因此数列{an}的通项公式为解题回顾:公式 ,给出了数列的项与和
之间的关系,很重要.在利用这个关系时必须注意:
(1)公式对任何数列都适用;
(2)n=1的情形要单独讨论.7.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法解题分析:本题主要利用S3,S9,S6成等差数列这个条件.解: (1)法一:由S3,S9,S6成等差数列,得S3+S6=2S9若q=1,则S3+S6=9a1 , 2S9=18a1由a1≠0,得S3+S6≠2S9, 与题意不符,所以q≠1由S3+S6=2S9 得整理,得q3+q6=2q9由q≠0,1,得q37.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法解: (1)法二:由S3,S9,S6成等差数列,得S9-S3=S6-S9∴a4+a5+a6+a7+a8+a9=-(a7+a8+a9)∴q3移项得a4+a5+a6+2(a7+a8+a9)= 0∴(a4+a5+a6)(1+2q3)= 0∵a4+a5+a6=a4(1+q+q2)≠ 07.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法解: (2)法一:由(1)知:a8=a2×q6= ,a5=a2×q3=a8-a2=a5-a8所以a2 ,a8 ,a5 成等差数列解: (2)法二:由(1)知:a2+a5-2a8=a2×(1+q3-2q6) 所以a2 ,a8 ,a5 成等差数列7.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法【解题回顾】本题方法较多,用等比数列Sn公式时一定
要注意讨论q. ?8.一个等差数列的前12项和为354,前12项中偶数项和与奇数项和之比为32∶27,求公差d.能力·思维·方法解题分析:此题若选用前n项和公式建立方程组显然运算量
大,而运用等差数列有关性质、采取整体思维的策略,则可大大简化计算过程。解:设前12项中偶数项与奇数项和为S偶、S奇,依题意
得由S偶-S奇=6d 所以 d=5 8.一个等差数列的前12项和为354,前12项中偶数项和与奇数项和之比为32∶27,求公差d.能力·思维·方法【解题回顾】在等差数列{an}中:
(1)项数为2n时,则S偶-S奇=nd,
(2)项数为2n-1时,则S奇-S偶=an,
S2n-1=(2n-1)an,当{an}为等比数列时其结论可类似推导得出.变式题1.已知等差数列{an}公差d=1,且a1+a 2+a3+…+a98=137
则a2+a4+a6+…+a98=___________能力·思维·方法解:S奇+S偶=137, S偶-S奇=49×1 2S偶=186, S偶=93 93解法二:am = an+(m-n) d a1 = a2-d, a3 = a4-d, a5 = a6-d, …… ,a97=a98-d∴a1 +a2+a3+…+a98
=(a1+a3+…+a97)+(a2+a4+…+a98)
=(a2+a4+…+a98-49d)+(a2+a4+…+a98)
=2(a2+a4+…+a98)-49= 137∴2(a2+a4+…+a98 )=186 变式题2.有一项数为2n=1的等差数列,求它的奇数项之和
与偶数项之和的比。能力·思维·方法解:设数列为{am},共2n+1项,奇数项和为S1,偶数项和
S2,则误解分析1.用公式an=Sn-Sn-1解决相关问题时,一定要注意条件n≥2,因n=1时,a1=S1. 2.等比数列的和或利用等比数列求和公式 解
题时,若忽视q=1的讨论.常会招致“对而不全”.
求和公式要点·疑点·考点3.在等差(比)数列中,Sn,S2n-Sn,S3n-S2n,…,Skn-S(k-1)n…成等差(比)数列.其中Sn为前n项的和. 1.等差数列前n项和
等比数列前n项和
2.如果某个数列前n项和为Sn,则2.已知等差数列{an}的前n项和为Sn,若a4=18-a5,则S8等于( )
A.18 B.36 C.54 D.72 基础题例题1.在某报《自测健康状况》的报道中,自测血压结果与相应年龄的统计数据如下表,观察表中数据的特点,用适当的数填入表中空白( )内.14085D5.在等差数列{an}中,a2+a4=p,a3+a5=q.则其前6项的
和S6为 ( )
(A) 5 (p+q)/4 (B) 3(p+q)/2 (C) p+q (D) 2(p+q)4.等比数列{an}前n项的乘积为Tn,若Tn=1,T2n=2,则T3n的值为( )
(A)3 (B)4 (C)7 (D)8 DB3.设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q=___1 an=Sn-Sn-1=d (常数)Tn, T2n/Tn, T3n/T2n 也成等比数列基础题例题能力·思维·方法6.设数列{an}的前n项和为Sn=2n2+3n+2,求通项an的表达式,并指出此数列是否为等差数列.解题分析:利用Sn与an的关系,可以求出an.解:n=1时,a1=S1=7,n≥2时,an=Sn-Sn-1=2n2+3n+2-[2(n-1)2+3(n-1)+2]
∴an=4n+1因此数列{an}的通项公式为解题回顾:公式 ,给出了数列的项与和
之间的关系,很重要.在利用这个关系时必须注意:
(1)公式对任何数列都适用;
(2)n=1的情形要单独讨论.7.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法解题分析:本题主要利用S3,S9,S6成等差数列这个条件.解: (1)法一:由S3,S9,S6成等差数列,得S3+S6=2S9若q=1,则S3+S6=9a1 , 2S9=18a1由a1≠0,得S3+S6≠2S9, 与题意不符,所以q≠1由S3+S6=2S9 得整理,得q3+q6=2q9由q≠0,1,得q37.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法解: (1)法二:由S3,S9,S6成等差数列,得S9-S3=S6-S9∴a4+a5+a6+a7+a8+a9=-(a7+a8+a9)∴q3移项得a4+a5+a6+2(a7+a8+a9)= 0∴(a4+a5+a6)(1+2q3)= 0∵a4+a5+a6=a4(1+q+q2)≠ 07.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法解: (2)法一:由(1)知:a8=a2×q6= ,a5=a2×q3=a8-a2=a5-a8所以a2 ,a8 ,a5 成等差数列解: (2)法二:由(1)知:a2+a5-2a8=a2×(1+q3-2q6) 所以a2 ,a8 ,a5 成等差数列7.已知等比数列{an}的公比为q,前n项的和为Sn,且
S3,S9,S6成等差数列.
(1)求q3的值; (2)求证a2,a8,a5成等差数列. 能力·思维·方法【解题回顾】本题方法较多,用等比数列Sn公式时一定
要注意讨论q. ?8.一个等差数列的前12项和为354,前12项中偶数项和与奇数项和之比为32∶27,求公差d.能力·思维·方法解题分析:此题若选用前n项和公式建立方程组显然运算量
大,而运用等差数列有关性质、采取整体思维的策略,则可大大简化计算过程。解:设前12项中偶数项与奇数项和为S偶、S奇,依题意
得由S偶-S奇=6d 所以 d=5 8.一个等差数列的前12项和为354,前12项中偶数项和与奇数项和之比为32∶27,求公差d.能力·思维·方法【解题回顾】在等差数列{an}中:
(1)项数为2n时,则S偶-S奇=nd,
(2)项数为2n-1时,则S奇-S偶=an,
S2n-1=(2n-1)an,当{an}为等比数列时其结论可类似推导得出.变式题1.已知等差数列{an}公差d=1,且a1+a 2+a3+…+a98=137
则a2+a4+a6+…+a98=___________能力·思维·方法解:S奇+S偶=137, S偶-S奇=49×1 2S偶=186, S偶=93 93解法二:am = an+(m-n) d a1 = a2-d, a3 = a4-d, a5 = a6-d, …… ,a97=a98-d∴a1 +a2+a3+…+a98
=(a1+a3+…+a97)+(a2+a4+…+a98)
=(a2+a4+…+a98-49d)+(a2+a4+…+a98)
=2(a2+a4+…+a98)-49= 137∴2(a2+a4+…+a98 )=186 变式题2.有一项数为2n=1的等差数列,求它的奇数项之和
与偶数项之和的比。能力·思维·方法解:设数列为{am},共2n+1项,奇数项和为S1,偶数项和
S2,则误解分析1.用公式an=Sn-Sn-1解决相关问题时,一定要注意条件n≥2,因n=1时,a1=S1. 2.等比数列的和或利用等比数列求和公式 解
题时,若忽视q=1的讨论.常会招致“对而不全”.
