人教版五年级上册数学总复习第1课时小数乘、除法课件(共49张PPT)
文档属性
| 名称 | 人教版五年级上册数学总复习第1课时小数乘、除法课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 07:01:21 | ||
图片预览










文档简介
(共49张PPT)
第1课时 小数乘、除法
总复习
8
义务教育人教版五年级上册
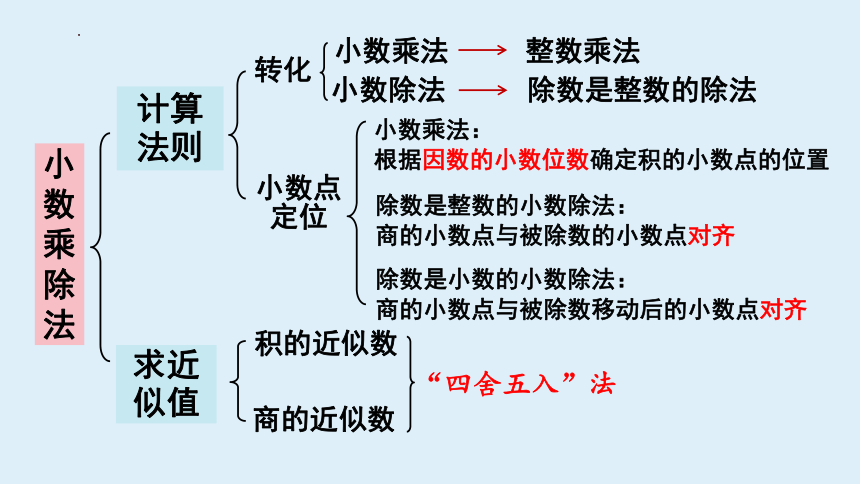
计算
法则
小
数
乘
除
法
求近
似值
转化
小数点定位
小数乘法
整数乘法
小数除法
除数是整数的除法
小数乘法:
根据因数的小数位数确定积的小数点的位置
“四舍五入”法
除数是整数的小数除法:
商的小数点与被除数的小数点对齐
除数是小数的小数除法:
商的小数点与被除数移动后的小数点对齐
积的近似数
商的近似数
小
数
乘
除
法
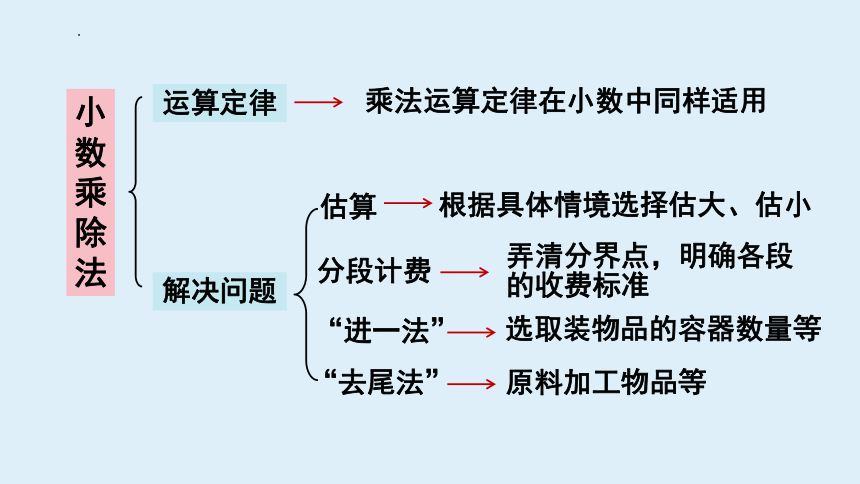
运算定律
解决问题
乘法运算定律在小数中同样适用
估算
分段计费
“进一法”
“去尾法”
根据具体情境选择估大、估小
弄清分界点,明确各段的收费标准
选取装物品的容器数量等
原料加工物品等
例1 用简便方法计算。
=0.55×100+0.55×1
=0.55×(100+1)
=55+0.55
=55.55
0.55×101
(1)
1.21×6.3+0.79×6.3
=(1.21+0.79)×6.3
= 2×6.3
=12.6
7.25×0.25×4
=7.25×(0.25×4)
=7.25×1
=7.25
(2)
(3)
根据数据特点运用合适的乘法运算定律,可以使一些小数连乘、乘加、乘减的计算简便。
例1 用简便方法计算。
例2 出租车收费标准:3km以内10元,超过3km,
每千米2元(不足1km按1km计算)。玲玲乘
车行驶了9km,她应付多少元?
10+(9-3)×2
=10+12
=22(元)
解决此类问题时,要弄清分界点,明确每一段的收费标准,再用乘加或乘减分段计算。
答:她应付22元。
例3 生活中的数学
(1)每个油桶可以装2.5kg豆油。56kg豆油至少需要
这样的油桶多少个?
56÷2.5=22.4(个)≈23(个)
答:至少需要这样的油桶23个。
例3 生活中的数学
(2)某超市要为服务员做工作服,一共准备了200m
布,做一套工作服要2.2m布,这些布最多能做
多少套工作服?
答:这些布最多能做90套工作服。
200÷2.2=90.90(套)≈90(套)
.
.
1.(1)27×3= , 24÷6 = ,
2.7×3= , 2.4÷6 = ,
2.7×0.3= , 2.4÷0.6 = ,
2.7×0.03= , 2.4÷0.06 = ,
81
8.1
0.81
0.081
4
0.4
4
40
巩固运用
(教材P110 T1)
1.(2)林华的妈妈去市场买水果。她先花10元买了
2.5kg橙子,还准备买3kg苹果,苹果的单价
是橙子的1.6倍。买苹果应付多少钱?
10÷2.5×1.6×3=19.2(元)
答:买苹果应付19.2元。
2.计算下面各题。
32.5÷2.5 1.36×0.05 0.06×1.7 2.08×75 65÷2.6 2.3÷0.46
=13
=0.068
=0.102
=156
=25
=5
(教材P112 练习二十五T2)
3.根据我们学过的运算律,在下面的 里
填上合适的数,在 里填上合适的运算符号。
31.8× =1.2×
(2.5+3.5)× = × ×4
(1.5×1.2)× =1.2×( ×6)
1.2
31.8
4
2.5
4
+
3.5
6
1.5
(教材P112 练习二十五T3)
(教材P114 练习二十五T15)
4.在下面的○里填上“>”或“<”。
9.9×6.9 70 0.97×23.8 24 57.5×6.2 420
15.6×2.1 30 26.4×1.08 26.4 5.9×7.8 48
<
<
<
<
>
>
5.用简便方法计算下面各题。
12.5×0.4×2.5×8
=(12.5×8)×(0.4×2.5)
= 100
= 9.5×(100+1)
= 959.5
9.5×101
3.65×2.8+3.65×7.2
=3.65×(2.8+7.2)
=36.5
4.2×7.8+2.2×4.2
=4.2×(7.8+2.2)
=42
6.一个修路队7.5小时修路136.5m,照这样计算,
8小时可修路多少米?
136.5÷7.5×8=145.6(m)
答:8小时可以修路145.6米。
课堂小结
通过这节课的学习,
你有什么收获
位置
用数对表示位置
根据数对确定位置
特点
数对中第一个数相同
同一列
同一行
数对中第二个数相同
先找列,再找行
(列数,行数)
先数在第几列,再数在第几行。
知识回顾
(1)在四(2)班教室里,陈丽坐的位置用数对表示是(4,6),张亮坐在陈丽的前面,他的位置用数对表示是( , );王刚是陈丽的同桌,他坐的位置用数对表示可能是( , )或( , )。
3 6
填一填。
4 5
5 6
(2)在同一平面内的点A(3,5)和点B(4,5),点( )在点( )的右面;在同一平面内的点A(5,2)和点B(5,4),点( )在点( )的前面。
B
A
A
B
多边形的面积
基本图形的面积
S平行四边形=ah
S三角形=ah÷2
S梯形=(a+b)h÷2
组合图形的面积
割补法
不规则图形的面积
估算
下面这块地种了三种蔬菜。茄子、黄瓜和西红柿各种了多少平方米?这块地共有多少平方米?
(教材P110 T2)
15m
15m
25m
23m
32m
茄子:15×32÷2=240(m2)
黄瓜:25×32=800(m2)
西红柿:(15+23)×32÷2=608(m2)
总面积:240+800+608=1648(m2)
答:茄子种了240m2,黄瓜种了800m2,西红柿种了608m2,这块地共有1648m2。
1. 先用数对表示点A、B、C的位置,再在图上标出D(3,4)、E(5,1)的位置,并顺次连接A、D、E、C、A,围成的是什么图形?
.
D
.
E
顺次连接A、D、E、C、A,围成的是平行四边形。
A(6,5)、B(1,1)、
C(8,2)。
巩固运用
2. 在图中描出(1,1)、(2,2)、(3,3)、(4,4)、(5,5)所表示的点,再把这些点连接起来。
.
.
.
.
.
这些点连接起来是一条线段。
你能说出他们每一手棋所下的位置吗?
3.两个同学在下五子棋
(教材P111 T4)
①(H,7)
②(I,8)
③(I,7)
④(J,8)
⑤(J,7)
⑥(G,7)
⑦(I,6)
⑧(J,5)
⑨(J,6)
⑩(K,7)
(H,8)
(G,9)
(L,6)
(K,6)
(K,8)
(H,5)
(F,8)
(G,6)
(G,8)
(I,4)
(J,3)
21
(H,3)
22
(L,7)
23
(G,2)
24
4.选择题。
(1)已知梯形的面积是42.5dm2,上底是3dm,下底
是7dm,求它的高正确列式是( )。
A. 42.5×2÷(3+7) B. 42.5÷(3+7)
C. 42.5÷(3+7-3) D. 42.5×2÷(7-3)
(2)如下图,阴影部分的面积( )空白部分的面积。
A. > B. =
C. < D.无法确定
A
B
(3)一个三角形与一个平行四边形的面积相等,底
也相等。如果三角形的高是6cm,那么平行四
边形的高是( )cm。
A. 3 B. 6 C. 12 D. 18
(4)一堆钢管,最上层4根,最下层10根,相邻两层
均相差1根,这堆钢管共( )根。
A. 35 B. 42 C. 49 D. 52
A
C
每个梯形的高度是:
(6.6-0.6)÷ 2=3(cm)
(4+0.4)×3÷2×2+0.4×0.6=13.44(cm2)
答:沙漏横截面的面积是13.44cm2 。
5.沙漏是古代的一种计量时间的工具。你能算
出如图所示沙漏横截面的面积吗?(单位:cm)
6.6
4
0.4
0.6
6.把一张边长4cm的正方形纸,沿相邻两边中点的连
线剪去一个角(如下图),剩下的面积是多少?
补全正方形。
4×4-(4÷2)×(4÷2÷2)
=14(cm2)
答:剩下的面积是14cm2。
(教材P113 练习二十五T9)
7. 您能想办法计算下图的面积吗?(小方格的边
长为1cm。)
把这个图形分成三个三角形和一个正方形。
7×2÷2+5×2÷2+5×1÷2+5×5=39.5(cm2)
(方法不唯一)
(教材P113 练习二十五T10)
课堂小结
通过这节课的学习,
你有什么收获
可能性
描述
可预知的:一定、不可能
不可预知的:可能
判断可能性大小
数量多 可能性大
数量少 可能性小
应
用
根据可能性大小推测数量的多少
知识回顾
植树问题
两端都植树
棵数=间隔数+1
两端都不植树
棵数=间隔数-1
一端植树,一端不植树
棵数=间隔数
封闭曲线上植树
棵数=间隔数
指针停在哪种颜色区域的可能性最大?停在哪
种颜色区域的可能性最小?
第一个转盘:
红色区域的可能性最大,黄色区域的可能性最小。
第二个转盘:
蓝色区域的可能性最大,红色区域的可能性最小。
1.
(教材P114 练习二十五T11)
巩固运用
2.
第一枚 正面 正面 反面 反面
第二枚 正面 反面 正面 反面
(教材P114 练习二十五T12)
如果两枚硬币朝上的面相同,我获胜。
会有哪些可能的结果?
3.学校召开运动会,同学们在一条直跑道一旁每隔4m
插一面小旗(起点、终点都插),一共插了26面。
如果改为每隔5m插一面,需要插多少面小旗?
(26-1)×4÷5+1=21(面)
答:需要插21面小旗。
4.李叔叔在正方形池塘边上植树,每边植树10棵
(四个角都植树),每两棵树之间相距4m。池塘
的面积是多少平方米?
(10-1)×4=36(m)
36×36=1296(m )
答:池塘的面积是1296m 。
5.吴老师家在第11层,他从第1层走到第3层用了40秒,
照这样计算,他还需要走多少秒才能到家?
40÷(3-1)=20(秒)
20×(11-3) =160(秒)
答:他还需要走160秒才能到家。
本讲主线
1、四边形中蝴蝶模型
(1)S1×S3=S2×S4
(2)△ABD=AO
△CBD OC
如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个 部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?
例题【一】(★ ★ )
根据蝴蝶模型可得:
△AOD=3×1÷2=1.5
四边形ABCD的面积:
1+2+3+1.5=7.5
人工湖的面积:7.5-6.92=0.58(平方千米)
如图,平行四边形ABCD的对角线交于O点,△CEF、△OEF、
板块二:梯形中的蝴蝶模型△ODF、△BOE的面积依次是2、4、4和6.求:
例题【二】(★ ★ ★)
(1)求△OCF的面积;
(2)求△GCE的面积,
(1)△BCD=2+4+4+6=16
△BCO=△CDO=8
△OCF=8-4=4
如图,平行四边形ABCD的对角线交于O点,△CEF、△OEF、
板块二:梯形中的蝴蝶模型△ODF、△BOE的面积依次是2、4、4和6.求:
例题【二】(★ ★ ★)
(1)求△OCF的面积;
(2)求△GCE的面积,
(2)△OEC=8-6=2
根据蝴蝶模型:
OG=△OEF=4=2
GC △ECF 2 1 ∴△GCE=2×1=2
3 3
知识链接
2、梯形中的蝴蝶模型
(1)S1×S3=S2×S4
(2)S1:S2:S3:S4=a2:ab:b2:ab
(3)AO=DO=a
OC OB b
如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知△AOB与△BOC的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是多少平方厘米.
例题【三】(★ ★ ★)
△1OCD=35×35÷25
=35×35
25
=49
25+35×2+49=144(平方厘米)
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
例题【四】(★ ★ ★ ★ )
梯形中的面积份数,9:25:15:15
共计:64份
一份:4÷64=1
16
△OAB=1×25=25
16 16
例题【五】(★ ★ ★ ★)
如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4平方厘米,△CED的面积是6平方厘米.问:四边形ABEF的面积是多少?
连接BF,得到梯形FBCD
△FCE=6
根据蝴蝶模型:
△BCE=6×6÷4=9
根据一半模型:
四ABEF=9+6-4=11
超常大挑战
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为 平方厘米
连接ED、FC、得到梯形EBCF 长=12×2=24
根据梯形蝴蝶模型:24-5-2-8=9
△EDO=△OCF=4
△FDC=8+4=12
知识链接
1、四边形中蝴蝶模型
(1)S1×S3=S2×S4
(2)△ABC=AO
△CBD OC
2.梯形中的蝴蝶模型
(1)S1×S3=S2×1
(2)S1:S2:S3:S4=a2:ab:b2:ab
第1课时 小数乘、除法
总复习
8
义务教育人教版五年级上册
计算
法则
小
数
乘
除
法
求近
似值
转化
小数点定位
小数乘法
整数乘法
小数除法
除数是整数的除法
小数乘法:
根据因数的小数位数确定积的小数点的位置
“四舍五入”法
除数是整数的小数除法:
商的小数点与被除数的小数点对齐
除数是小数的小数除法:
商的小数点与被除数移动后的小数点对齐
积的近似数
商的近似数
小
数
乘
除
法
运算定律
解决问题
乘法运算定律在小数中同样适用
估算
分段计费
“进一法”
“去尾法”
根据具体情境选择估大、估小
弄清分界点,明确各段的收费标准
选取装物品的容器数量等
原料加工物品等
例1 用简便方法计算。
=0.55×100+0.55×1
=0.55×(100+1)
=55+0.55
=55.55
0.55×101
(1)
1.21×6.3+0.79×6.3
=(1.21+0.79)×6.3
= 2×6.3
=12.6
7.25×0.25×4
=7.25×(0.25×4)
=7.25×1
=7.25
(2)
(3)
根据数据特点运用合适的乘法运算定律,可以使一些小数连乘、乘加、乘减的计算简便。
例1 用简便方法计算。
例2 出租车收费标准:3km以内10元,超过3km,
每千米2元(不足1km按1km计算)。玲玲乘
车行驶了9km,她应付多少元?
10+(9-3)×2
=10+12
=22(元)
解决此类问题时,要弄清分界点,明确每一段的收费标准,再用乘加或乘减分段计算。
答:她应付22元。
例3 生活中的数学
(1)每个油桶可以装2.5kg豆油。56kg豆油至少需要
这样的油桶多少个?
56÷2.5=22.4(个)≈23(个)
答:至少需要这样的油桶23个。
例3 生活中的数学
(2)某超市要为服务员做工作服,一共准备了200m
布,做一套工作服要2.2m布,这些布最多能做
多少套工作服?
答:这些布最多能做90套工作服。
200÷2.2=90.90(套)≈90(套)
.
.
1.(1)27×3= , 24÷6 = ,
2.7×3= , 2.4÷6 = ,
2.7×0.3= , 2.4÷0.6 = ,
2.7×0.03= , 2.4÷0.06 = ,
81
8.1
0.81
0.081
4
0.4
4
40
巩固运用
(教材P110 T1)
1.(2)林华的妈妈去市场买水果。她先花10元买了
2.5kg橙子,还准备买3kg苹果,苹果的单价
是橙子的1.6倍。买苹果应付多少钱?
10÷2.5×1.6×3=19.2(元)
答:买苹果应付19.2元。
2.计算下面各题。
32.5÷2.5 1.36×0.05 0.06×1.7 2.08×75 65÷2.6 2.3÷0.46
=13
=0.068
=0.102
=156
=25
=5
(教材P112 练习二十五T2)
3.根据我们学过的运算律,在下面的 里
填上合适的数,在 里填上合适的运算符号。
31.8× =1.2×
(2.5+3.5)× = × ×4
(1.5×1.2)× =1.2×( ×6)
1.2
31.8
4
2.5
4
+
3.5
6
1.5
(教材P112 练习二十五T3)
(教材P114 练习二十五T15)
4.在下面的○里填上“>”或“<”。
9.9×6.9 70 0.97×23.8 24 57.5×6.2 420
15.6×2.1 30 26.4×1.08 26.4 5.9×7.8 48
<
<
<
<
>
>
5.用简便方法计算下面各题。
12.5×0.4×2.5×8
=(12.5×8)×(0.4×2.5)
= 100
= 9.5×(100+1)
= 959.5
9.5×101
3.65×2.8+3.65×7.2
=3.65×(2.8+7.2)
=36.5
4.2×7.8+2.2×4.2
=4.2×(7.8+2.2)
=42
6.一个修路队7.5小时修路136.5m,照这样计算,
8小时可修路多少米?
136.5÷7.5×8=145.6(m)
答:8小时可以修路145.6米。
课堂小结
通过这节课的学习,
你有什么收获
位置
用数对表示位置
根据数对确定位置
特点
数对中第一个数相同
同一列
同一行
数对中第二个数相同
先找列,再找行
(列数,行数)
先数在第几列,再数在第几行。
知识回顾
(1)在四(2)班教室里,陈丽坐的位置用数对表示是(4,6),张亮坐在陈丽的前面,他的位置用数对表示是( , );王刚是陈丽的同桌,他坐的位置用数对表示可能是( , )或( , )。
3 6
填一填。
4 5
5 6
(2)在同一平面内的点A(3,5)和点B(4,5),点( )在点( )的右面;在同一平面内的点A(5,2)和点B(5,4),点( )在点( )的前面。
B
A
A
B
多边形的面积
基本图形的面积
S平行四边形=ah
S三角形=ah÷2
S梯形=(a+b)h÷2
组合图形的面积
割补法
不规则图形的面积
估算
下面这块地种了三种蔬菜。茄子、黄瓜和西红柿各种了多少平方米?这块地共有多少平方米?
(教材P110 T2)
15m
15m
25m
23m
32m
茄子:15×32÷2=240(m2)
黄瓜:25×32=800(m2)
西红柿:(15+23)×32÷2=608(m2)
总面积:240+800+608=1648(m2)
答:茄子种了240m2,黄瓜种了800m2,西红柿种了608m2,这块地共有1648m2。
1. 先用数对表示点A、B、C的位置,再在图上标出D(3,4)、E(5,1)的位置,并顺次连接A、D、E、C、A,围成的是什么图形?
.
D
.
E
顺次连接A、D、E、C、A,围成的是平行四边形。
A(6,5)、B(1,1)、
C(8,2)。
巩固运用
2. 在图中描出(1,1)、(2,2)、(3,3)、(4,4)、(5,5)所表示的点,再把这些点连接起来。
.
.
.
.
.
这些点连接起来是一条线段。
你能说出他们每一手棋所下的位置吗?
3.两个同学在下五子棋
(教材P111 T4)
①(H,7)
②(I,8)
③(I,7)
④(J,8)
⑤(J,7)
⑥(G,7)
⑦(I,6)
⑧(J,5)
⑨(J,6)
⑩(K,7)
(H,8)
(G,9)
(L,6)
(K,6)
(K,8)
(H,5)
(F,8)
(G,6)
(G,8)
(I,4)
(J,3)
21
(H,3)
22
(L,7)
23
(G,2)
24
4.选择题。
(1)已知梯形的面积是42.5dm2,上底是3dm,下底
是7dm,求它的高正确列式是( )。
A. 42.5×2÷(3+7) B. 42.5÷(3+7)
C. 42.5÷(3+7-3) D. 42.5×2÷(7-3)
(2)如下图,阴影部分的面积( )空白部分的面积。
A. > B. =
C. < D.无法确定
A
B
(3)一个三角形与一个平行四边形的面积相等,底
也相等。如果三角形的高是6cm,那么平行四
边形的高是( )cm。
A. 3 B. 6 C. 12 D. 18
(4)一堆钢管,最上层4根,最下层10根,相邻两层
均相差1根,这堆钢管共( )根。
A. 35 B. 42 C. 49 D. 52
A
C
每个梯形的高度是:
(6.6-0.6)÷ 2=3(cm)
(4+0.4)×3÷2×2+0.4×0.6=13.44(cm2)
答:沙漏横截面的面积是13.44cm2 。
5.沙漏是古代的一种计量时间的工具。你能算
出如图所示沙漏横截面的面积吗?(单位:cm)
6.6
4
0.4
0.6
6.把一张边长4cm的正方形纸,沿相邻两边中点的连
线剪去一个角(如下图),剩下的面积是多少?
补全正方形。
4×4-(4÷2)×(4÷2÷2)
=14(cm2)
答:剩下的面积是14cm2。
(教材P113 练习二十五T9)
7. 您能想办法计算下图的面积吗?(小方格的边
长为1cm。)
把这个图形分成三个三角形和一个正方形。
7×2÷2+5×2÷2+5×1÷2+5×5=39.5(cm2)
(方法不唯一)
(教材P113 练习二十五T10)
课堂小结
通过这节课的学习,
你有什么收获
可能性
描述
可预知的:一定、不可能
不可预知的:可能
判断可能性大小
数量多 可能性大
数量少 可能性小
应
用
根据可能性大小推测数量的多少
知识回顾
植树问题
两端都植树
棵数=间隔数+1
两端都不植树
棵数=间隔数-1
一端植树,一端不植树
棵数=间隔数
封闭曲线上植树
棵数=间隔数
指针停在哪种颜色区域的可能性最大?停在哪
种颜色区域的可能性最小?
第一个转盘:
红色区域的可能性最大,黄色区域的可能性最小。
第二个转盘:
蓝色区域的可能性最大,红色区域的可能性最小。
1.
(教材P114 练习二十五T11)
巩固运用
2.
第一枚 正面 正面 反面 反面
第二枚 正面 反面 正面 反面
(教材P114 练习二十五T12)
如果两枚硬币朝上的面相同,我获胜。
会有哪些可能的结果?
3.学校召开运动会,同学们在一条直跑道一旁每隔4m
插一面小旗(起点、终点都插),一共插了26面。
如果改为每隔5m插一面,需要插多少面小旗?
(26-1)×4÷5+1=21(面)
答:需要插21面小旗。
4.李叔叔在正方形池塘边上植树,每边植树10棵
(四个角都植树),每两棵树之间相距4m。池塘
的面积是多少平方米?
(10-1)×4=36(m)
36×36=1296(m )
答:池塘的面积是1296m 。
5.吴老师家在第11层,他从第1层走到第3层用了40秒,
照这样计算,他还需要走多少秒才能到家?
40÷(3-1)=20(秒)
20×(11-3) =160(秒)
答:他还需要走160秒才能到家。
本讲主线
1、四边形中蝴蝶模型
(1)S1×S3=S2×S4
(2)△ABD=AO
△CBD OC
如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个 部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?
例题【一】(★ ★ )
根据蝴蝶模型可得:
△AOD=3×1÷2=1.5
四边形ABCD的面积:
1+2+3+1.5=7.5
人工湖的面积:7.5-6.92=0.58(平方千米)
如图,平行四边形ABCD的对角线交于O点,△CEF、△OEF、
板块二:梯形中的蝴蝶模型△ODF、△BOE的面积依次是2、4、4和6.求:
例题【二】(★ ★ ★)
(1)求△OCF的面积;
(2)求△GCE的面积,
(1)△BCD=2+4+4+6=16
△BCO=△CDO=8
△OCF=8-4=4
如图,平行四边形ABCD的对角线交于O点,△CEF、△OEF、
板块二:梯形中的蝴蝶模型△ODF、△BOE的面积依次是2、4、4和6.求:
例题【二】(★ ★ ★)
(1)求△OCF的面积;
(2)求△GCE的面积,
(2)△OEC=8-6=2
根据蝴蝶模型:
OG=△OEF=4=2
GC △ECF 2 1 ∴△GCE=2×1=2
3 3
知识链接
2、梯形中的蝴蝶模型
(1)S1×S3=S2×S4
(2)S1:S2:S3:S4=a2:ab:b2:ab
(3)AO=DO=a
OC OB b
如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知△AOB与△BOC的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是多少平方厘米.
例题【三】(★ ★ ★)
△1OCD=35×35÷25
=35×35
25
=49
25+35×2+49=144(平方厘米)
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
例题【四】(★ ★ ★ ★ )
梯形中的面积份数,9:25:15:15
共计:64份
一份:4÷64=1
16
△OAB=1×25=25
16 16
例题【五】(★ ★ ★ ★)
如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4平方厘米,△CED的面积是6平方厘米.问:四边形ABEF的面积是多少?
连接BF,得到梯形FBCD
△FCE=6
根据蝴蝶模型:
△BCE=6×6÷4=9
根据一半模型:
四ABEF=9+6-4=11
超常大挑战
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为 平方厘米
连接ED、FC、得到梯形EBCF 长=12×2=24
根据梯形蝴蝶模型:24-5-2-8=9
△EDO=△OCF=4
△FDC=8+4=12
知识链接
1、四边形中蝴蝶模型
(1)S1×S3=S2×S4
(2)△ABC=AO
△CBD OC
2.梯形中的蝴蝶模型
(1)S1×S3=S2×1
(2)S1:S2:S3:S4=a2:ab:b2:ab
