第五章 平行四边形 单元测试题 (含答案) 鲁教版(五四制)上学期八年级数学
文档属性
| 名称 | 第五章 平行四边形 单元测试题 (含答案) 鲁教版(五四制)上学期八年级数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 339.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 13:28:57 | ||
图片预览



文档简介
2023-2024学年上学期八年级数学第五章平行四边形单元测试题
(120分钟 150分)
一、选择题(每小题4分,共40分)
1.(2022·湘潭中考)在 ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
A.80° B.100° C.120° D.140°
2.已知一个多边形的内角和是1 440°,则这个多边形的边数是( )
A.9 B.10 C.11 D.12
3.从一个多边形的顶点出发,可以作2条对角线,则这个多边形的内角和是 ( )
A.180° B.270° C.360° D.540°
4.(2022·河北中考)依据所标数据,下列一定为平行四边形的是(D)
5.如图,平行四边形ABCD中,E,F分别在边AD,BC上,DE=BF=3,EF⊥AD,若EF=8,AE=9,则AB的长为( )
A.10 B. C.9 D.6
1. 5. 6.
6.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.3对 B.2对 C.1对 D.0对
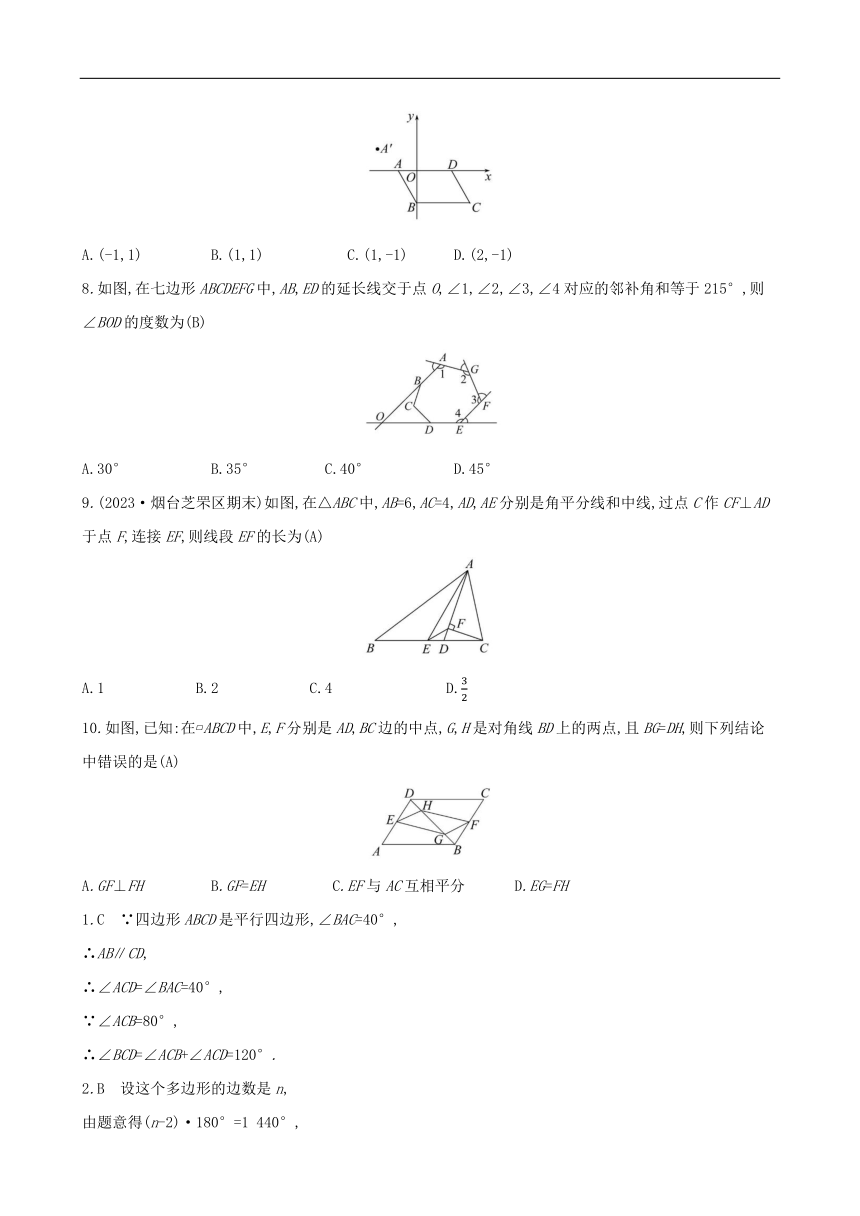
7. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A的坐标为(-1,0),点B的坐标为(0,-2),点D的坐标为(2,0),将 ABCD平移,使点A移动到点A'(-2,1)处,则平移后C点的对应点C'的坐标为( )
A.(-1,1) B.(1,1) C.(1,-1) D.(2,-1)
8.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,∠1,∠2,∠3,∠4对应的邻补角和等于215°,则∠BOD的度数为( )
A.30° B.35° C.40° D.45°
7. 8. 9.
9.(2023·烟台芝罘区期末)如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为( )
A.1 B.2 C.4 D.
10.如图,已知:在 ABCD中,E,F分别是AD,BC边的中点,G,H是对角线BD上的两点,且BG=DH,则下列结论中错误的是( )
A.GF⊥FH B.GF=EH C.EF与AC互相平分 D.EG=FH
二、填空题(每小题4分,共20分)
11.(2022·南充中考)数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC,BC两边中点的距离DE为10 m(如图),则A,B两点的距离是 m.
10 11. 12.
12.如图,将△ABC沿它的中位线MN折叠后,点A落在点A'处,若∠A=30°,∠B=115°,则∠A'NC= °.
13.如图,在正六边形ABCDEF中,AE与DF交于点O,则∠1的度数为 .
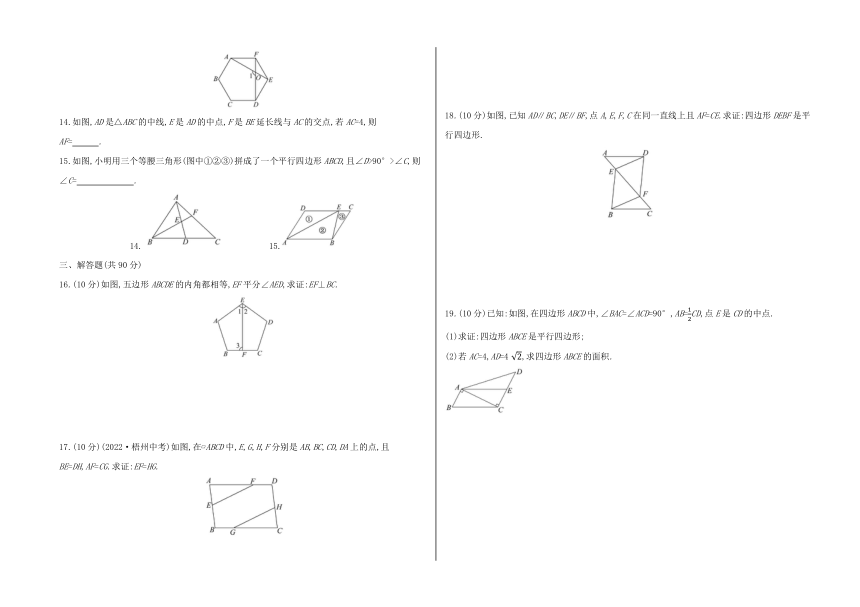
14.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF= .
15.如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且∠D>90°>∠C,则∠C= .
14. 15.
三、解答题(共90分)
16.(10分)如图,五边形ABCDE的内角都相等,EF平分∠AED,求证:EF⊥BC.
17.(10分)(2022·梧州中考)如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
18.(10分)如图,已知AD∥BC,DE∥BF,点A,E,F,C在同一直线上且AF=CE.求证:四边形DEBF是平行四边形.
19.(10分)已知:如图,在四边形ABCD中,∠BAC=∠ACD=90°,AB=CD,点E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=4,AD=4,求四边形ABCE的面积.
20.(12分)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)证明:AC=EF;
(2)求证:四边形ADFE是平行四边形.
21.(12分)(2023·烟台招远市期末)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接AF,FG,H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
22.(13分)如图,矩形ABCD中,AB=4 cm,BC=8 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以
1 cm/s的速度运动,设运动时间为t s.
(1)若动点M,N同时出发,t秒时,N走过_________cm,M走过_________cm;
(2)若动点M,N同时出发,经过几秒钟两点第一次相遇
(3)若点E在线段BC上,且BE=3 cm,若动点M,N同时出发,相遇时停止运动,经过几秒钟,点A,E,M,N组成平行四边形
23. (13分)(2022·沈阳质检)如图,点B是∠MAN的边AM上的定点,点C是边AN上的动点,将△ABC绕点B逆时针旋转得到△DBE,且点A的对应点D恰好落在边AN上,连接CE.当BC=AC时.
(1)求证:四边形ABEC是平行四边形;
(2)若AB=15,AD=18,求AC的长.
2023-2024学年上学期八年级数学第五章平行四边形单元测试题
(120分钟 150分)
一、选择题(每小题4分,共40分)
1.(2022·湘潭中考)在 ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=(C)
A.80° B.100° C.120° D.140°
2.已知一个多边形的内角和是1 440°,则这个多边形的边数是(B)
A.9 B.10 C.11 D.12
3.从一个多边形的顶点出发,可以作2条对角线,则这个多边形的内角和是 (D)
A.180° B.270° C.360° D.540°
4.(2022·河北中考)依据所标数据,下列一定为平行四边形的是(D)
5.如图,平行四边形ABCD中,E,F分别在边AD,BC上,DE=BF=3,EF⊥AD,若EF=8,AE=9,则AB的长为(A)
A.10 B. C.9 D.6
6.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH的交点P在BD上,则图中面积相等的平行四边形有(A)
A.3对 B.2对 C.1对 D.0对
7. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A的坐标为(-1,0),点B的坐标为(0,-2),点D的坐标为(2,0),将 ABCD平移,使点A移动到点A'(-2,1)处,则平移后C点的对应点C'的坐标为(D)
A.(-1,1) B.(1,1) C.(1,-1) D.(2,-1)
8.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,∠1,∠2,∠3,∠4对应的邻补角和等于215°,则∠BOD的度数为(B)
A.30° B.35° C.40° D.45°
9.(2023·烟台芝罘区期末)如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为(A)
A.1 B.2 C.4 D.
10.如图,已知:在 ABCD中,E,F分别是AD,BC边的中点,G,H是对角线BD上的两点,且BG=DH,则下列结论中错误的是(A)
A.GF⊥FH B.GF=EH C.EF与AC互相平分 D.EG=FH
1.C ∵四边形ABCD是平行四边形,∠BAC=40°,
∴AB∥CD,
∴∠ACD=∠BAC=40°,
∵∠ACB=80°,
∴∠BCD=∠ACB+∠ACD=120°.
2.B 设这个多边形的边数是n,
由题意得(n-2)·180°=1 440°,
∴n=10.
3.D ∵多边形从一个顶点出发可引出2条对角线,
∴n-3=2,解得n=5.
∴内角和=(5-2)·180°=540°.
4.D A.80°+110°≠180°,故A选项不符合题意;
B.只有一组对边平行不能确定是平行四边形,故B选项不符合题意;
C.不能判断出任何一组对边是平行的,故C选项不符合题意;
D.有一组对边平行且相等是平行四边形,故D选项符合题意.
5.A 过点B作BH⊥AD于H,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EF⊥AD,BH⊥AD,∴BH∥EF,
∴四边形BHEF是平行四边形,
∵∠BHE=90°,
∴四边形BHEF为矩形,
∴HE=BF=3,EF=BH=8,
∵AE=9,
∴AH=AE-HE=9-3=6,
∴AB===10.
6.A ∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD.
∵BP是平行四边形BEPH的对角线,
∴S△BEP=S△BHP,
∵PD是平行四边形GPFD的对角线,
∴S△GPD=S△FPD.
∴S△ABD-S△BEP-S△GPD=S△BCD-S△BHP-S△PFD,
即S AEPG=S HCFP,
∴S ABHG=S BCFE,
同理S AEFD=S HCDG.
即S ABHG=S BCFE,S AEPG=S HCFP,S AEFD=S HCDG,
所以面积相等的平行四边形有3对.
7.D ∵四边形ABCD是平行四边形,
∴BC=AD,
∵点A的坐标为(-1,0),点B的坐标为(0,-2),点D的坐标为(2,0),
∴AD=BC=3,OB=2,∴C(3,-2),
∵将 ABCD平移,使点A(-1,0)移动到点A'(-2,1)处,
∴平移后C点的对应点C'的坐标为(2,-1).
8.B ∵∠1,∠2,∠3,∠4的邻补角的角度和为215°,
∴∠1+∠2+∠3+∠4+215°=4×180°,
∴∠1+∠2+∠3+∠4=505°,
∵五边形OAGFE内角和=(5-2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°-505°=35°.
9.A 延长CF交AB于G,
∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC=4,FG=CF,
∴BG=AB-AG=6-4=2.
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴EF=BG=1.
10.A 连接EF交BD于点O,
在平行四边形ABCD中,AD=BC,AD∥BC,∠EDH=∠FBG,
∵E,F分别是AD,BC边的中点,
∴DE=BF=BC,AE=BF,
∴四边形DEBF是平行四边形,四边形AEFB是平行四边形.
∴EF∥AB.
∵点E是AD的中点,∴点O是BD的中点.
根据平行四边形的对角线互相平分,故点O是AC的中点,也是EF的中点,故C不符合题意.
又∵BG=DH,∠EDH=∠FBG,DE=BF,
∴△DEH≌△BFG,
∴GF=EH,故B不符合题意.
∵∠DHE=∠BGF,
∴∠GHE=∠HGF.
又∵HG=GH,EH=FG,
∴△EHG≌△FGH,
∴EG=HF,故D不符合题意.
GF=EH,EG=HF,∴四边形EHFG是平行四边形,而不是矩形,故∠GFH不是90°,
∴A符合题意.
二、填空题(每小题4分,共20分)
11.(2022·南充中考)数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC,BC两边中点的距离DE为10 m(如图),则A,B两点的距离是 20 m.
12.如图,将△ABC沿它的中位线MN折叠后,点A落在点A'处,若∠A=30°,∠B=115°,则∠A'NC= 110 °.
13.如图,在正六边形ABCDEF中,AE与DF交于点O,则∠1的度数为 120° .
14.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF= .
15.如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且∠D>90°>∠C,则∠C= 72°或 .
11.【解析】∵CD=AD,CE=EB,
∴DE是△ABC的中位线,∴AB=2DE,
∵DE=10 m,∴AB=20 m.
答案:20
12.【解析】∵∠A=30°,∠B=115°,
∴∠C=180°-∠A-∠B=180°-30°-115°=35°,
∵MN是三角形的中位线,∴MN∥BC,
∴∠A'NM=∠ANM=∠C=35°,
∴∠A'NC=180°-∠ANM-∠A'NM=180°-35°-35°=110°.
答案:110
13.【解析】∵六边形ABCDEF是正六边形,
∴∠AFE=∠DEF=120°,AF=EF=DE,
∴∠FAE=∠FEA=∠EFD=(180°-120°)÷2=30°,
∴∠AFD=120°-30°=90°,
∴∠1=∠FAE+∠AFD=30°+90°=120°.
答案:120°
14.【解析】取BF的中点H,连接DH,
∵BD=DC,BH=HF,
∴DH=FC,DH∥AC,
∴∠HDE=∠FAE,
在△AEF和△DEH中,,
∴△AEF≌△DEH(ASA),
∴AF=DH,
∴AF=FC,
∵AC=4,
∴AF=.
答案:
15.【解析】由题意可知:AD=DE,
∴∠DAE=∠DEA,设∠DAE=∠DEA=x,
∵四边形ABCD是平行四边形,
∴CD∥AB,∠C=∠DAB,
∴∠DEA=∠EAB=x,
∴∠C=∠DAB=2x,
①AE=AB时,若BE=BC,
则有∠BEC=∠C,即(180°-x)=2x,
解得x=36°,
∴∠C=72°,
若EC=EB,则有∠EBC=∠C=2x,
∵∠DAB+∠ABC=180°,
∴4x+(180°-x)=180°,
解得x=,
∴∠C=,
②EA=EB时,同法可得∠C=72°,
综上所述,∠C=72°或.
答案:72°或
三、解答题(共90分)
16.(10分)如图,五边形ABCDE的内角都相等,EF平分∠AED,求证:EF⊥BC.
【证明】五边形的内角和为(5-2)×180°=540°,
∵5个内角都相等,
∴∠A=∠B=∠AED==108°,
∵EF平分∠AED,
∴∠1=∠2=54°,
∵四边形的内角和为360°,在四边形ABFE中,∠3=360°-(108°+108°+54°)=90°.
∴EF⊥BC.
17.(10分)(2022·梧州中考)如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
【证明】∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,
∵BE=DH,∴AB-BE=CD-DH,
即AE=CH,
在△AEF和△CHG中,,
∴△AEF≌△CHG(SAS),
∴EF=HG.
18.(10分)如图,已知AD∥BC,DE∥BF,点A,E,F,C在同一直线上且AF=CE.求证:四边形DEBF是平行四边形.
【证明】∵AD∥BC,DE∥BF,
∴∠A=∠C,∠DEF=∠BFE,
∴∠DEA=∠BFC,
∵AF=CE,
∴AF-EF=CE-EF,
∴AE=CF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴DE=BF,
∵DE∥BF,∴四边形DEBF是平行四边形.
19.(10分)已知:如图,在四边形ABCD中,∠BAC=∠ACD=90°,AB=CD,点E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=4,AD=4,求四边形ABCE的面积.
【解析】(1)∵∠BAC=∠ACD=90°,∴AB∥EC.
∵点E是CD的中点,∴EC=CD.
∵AB=CD,∴AB=EC.
∴四边形ABCE是平行四边形.
(2)∵∠ACD=90°,AC=4,AD=4,
∴CD==4.
∵AB=CD,∴AB=2.
∴S平行四边形ABCE=AB·AC=2×4=8.
20.(12分)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)证明:AC=EF;
(2)求证:四边形ADFE是平行四边形.
【证明】(1)∵在Rt△ABC中,∠BAC=30°,∴AB=2BC.
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.
在Rt△AFE和Rt△BCA中,
∴Rt△AFE≌Rt△BCA(HL).∴AC=EF.
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD.
∴∠DAB=∠DAC+∠BAC=90°.
又∵EF⊥AB,∴EF∥AD.
∵AC=EF,AC=AD,∴EF=AD.∴四边形ADFE是平行四边形.
21.(12分)(2023·烟台招远市期末)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接AF,FG,H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
【解析】(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∵BF=BE,CG=CE,∴BC是△EFG的中位线,
∴BC∥FG,BC=FG,
∵H为FG的中点,∴FH=FG,
∴BC∥FH,BC=FH,∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(2)∵∠BAE=80°,∴∠BCD=80°,
∵∠DCE=30°,∴∠BCE=80°-30°=50°,
∵CB=CE,∴∠CBE=∠CEB=(180°-50°)=65°.
22.(13分)如图,矩形ABCD中,AB=4 cm,BC=8 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以
1 cm/s的速度运动,设运动时间为t s.
(1)若动点M,N同时出发,t秒时,N走过_________cm,M走过_________cm;
(2)若动点M,N同时出发,经过几秒钟两点第一次相遇
(3)若点E在线段BC上,且BE=3 cm,若动点M,N同时出发,相遇时停止运动,经过几秒钟,点A,E,M,N组成平行四边形
【解析】(1)路程=时间×速度,时间为t,N的速度为1 cm/s,所以其路程为t,M的速度为2 cm/s,所以其路程为2t;
答案:t 2t
(2)根据题意得t+2t=2×(4+8)=24,
解得t=8,
即经过8秒钟两点第一次相遇;
(3)①如图1,点M在BC上且在E点右侧时,当AN=ME时,四边形AEMN为平行四边形,
得8-t=9-2t,
解得t=1,
此时点M在DC上,所以舍去;
②如图2,点M在BC上且在E点左侧时,当AN=ME时,四边形AMEN为平行四边形,
得8-t=2t-9,
解得t=,符合题意,
所以经过秒钟,点A,E,M,N组成平行四边形.
23. (13分)(2022·沈阳质检)如图,点B是∠MAN的边AM上的定点,点C是边AN上的动点,将△ABC绕点B逆时针旋转得到△DBE,且点A的对应点D恰好落在边AN上,连接CE.当BC=AC时.
(1)求证:四边形ABEC是平行四边形;
(2)若AB=15,AD=18,求AC的长.
【解析】(1)∵BC=AC,∴∠A=∠ABC.
∴∠BCD=∠A+∠ABC=2∠A.
∵△ABC绕点B逆时针旋转得到△DBE,
∴AB=BD,BC=BE,∠ABD=∠CBE.
∴∠BDA=∠A,∠BCE=∠BEC.∴∠A=∠BCE.
∵∠BCD=∠BCE+∠ECD,∴∠ECD=∠A=∠BEC.
∴AB∥CE,AC∥BE,∴四边形ABEC是平行四边形.
(2) 如图,过点B作BH⊥AD,垂足为H,
∵BD=BA,BH⊥AD,∴AH=AD=9.在Rt△ABH中,由勾股定理得,
BH===12.
设AC=BC=x,则CH=x-9.
在Rt△HCB中,由勾股定理得,(x-9)2+122=x2,
解得x=,即AC的长为.
(120分钟 150分)
一、选择题(每小题4分,共40分)
1.(2022·湘潭中考)在 ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
A.80° B.100° C.120° D.140°
2.已知一个多边形的内角和是1 440°,则这个多边形的边数是( )
A.9 B.10 C.11 D.12
3.从一个多边形的顶点出发,可以作2条对角线,则这个多边形的内角和是 ( )
A.180° B.270° C.360° D.540°
4.(2022·河北中考)依据所标数据,下列一定为平行四边形的是(D)
5.如图,平行四边形ABCD中,E,F分别在边AD,BC上,DE=BF=3,EF⊥AD,若EF=8,AE=9,则AB的长为( )
A.10 B. C.9 D.6
1. 5. 6.
6.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.3对 B.2对 C.1对 D.0对
7. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A的坐标为(-1,0),点B的坐标为(0,-2),点D的坐标为(2,0),将 ABCD平移,使点A移动到点A'(-2,1)处,则平移后C点的对应点C'的坐标为( )
A.(-1,1) B.(1,1) C.(1,-1) D.(2,-1)
8.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,∠1,∠2,∠3,∠4对应的邻补角和等于215°,则∠BOD的度数为( )
A.30° B.35° C.40° D.45°
7. 8. 9.
9.(2023·烟台芝罘区期末)如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为( )
A.1 B.2 C.4 D.
10.如图,已知:在 ABCD中,E,F分别是AD,BC边的中点,G,H是对角线BD上的两点,且BG=DH,则下列结论中错误的是( )
A.GF⊥FH B.GF=EH C.EF与AC互相平分 D.EG=FH
二、填空题(每小题4分,共20分)
11.(2022·南充中考)数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC,BC两边中点的距离DE为10 m(如图),则A,B两点的距离是 m.
10 11. 12.
12.如图,将△ABC沿它的中位线MN折叠后,点A落在点A'处,若∠A=30°,∠B=115°,则∠A'NC= °.
13.如图,在正六边形ABCDEF中,AE与DF交于点O,则∠1的度数为 .
14.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF= .
15.如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且∠D>90°>∠C,则∠C= .
14. 15.
三、解答题(共90分)
16.(10分)如图,五边形ABCDE的内角都相等,EF平分∠AED,求证:EF⊥BC.
17.(10分)(2022·梧州中考)如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
18.(10分)如图,已知AD∥BC,DE∥BF,点A,E,F,C在同一直线上且AF=CE.求证:四边形DEBF是平行四边形.
19.(10分)已知:如图,在四边形ABCD中,∠BAC=∠ACD=90°,AB=CD,点E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=4,AD=4,求四边形ABCE的面积.
20.(12分)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)证明:AC=EF;
(2)求证:四边形ADFE是平行四边形.
21.(12分)(2023·烟台招远市期末)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接AF,FG,H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
22.(13分)如图,矩形ABCD中,AB=4 cm,BC=8 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以
1 cm/s的速度运动,设运动时间为t s.
(1)若动点M,N同时出发,t秒时,N走过_________cm,M走过_________cm;
(2)若动点M,N同时出发,经过几秒钟两点第一次相遇
(3)若点E在线段BC上,且BE=3 cm,若动点M,N同时出发,相遇时停止运动,经过几秒钟,点A,E,M,N组成平行四边形
23. (13分)(2022·沈阳质检)如图,点B是∠MAN的边AM上的定点,点C是边AN上的动点,将△ABC绕点B逆时针旋转得到△DBE,且点A的对应点D恰好落在边AN上,连接CE.当BC=AC时.
(1)求证:四边形ABEC是平行四边形;
(2)若AB=15,AD=18,求AC的长.
2023-2024学年上学期八年级数学第五章平行四边形单元测试题
(120分钟 150分)
一、选择题(每小题4分,共40分)
1.(2022·湘潭中考)在 ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=(C)
A.80° B.100° C.120° D.140°
2.已知一个多边形的内角和是1 440°,则这个多边形的边数是(B)
A.9 B.10 C.11 D.12
3.从一个多边形的顶点出发,可以作2条对角线,则这个多边形的内角和是 (D)
A.180° B.270° C.360° D.540°
4.(2022·河北中考)依据所标数据,下列一定为平行四边形的是(D)
5.如图,平行四边形ABCD中,E,F分别在边AD,BC上,DE=BF=3,EF⊥AD,若EF=8,AE=9,则AB的长为(A)
A.10 B. C.9 D.6
6.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH的交点P在BD上,则图中面积相等的平行四边形有(A)
A.3对 B.2对 C.1对 D.0对
7. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A的坐标为(-1,0),点B的坐标为(0,-2),点D的坐标为(2,0),将 ABCD平移,使点A移动到点A'(-2,1)处,则平移后C点的对应点C'的坐标为(D)
A.(-1,1) B.(1,1) C.(1,-1) D.(2,-1)
8.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,∠1,∠2,∠3,∠4对应的邻补角和等于215°,则∠BOD的度数为(B)
A.30° B.35° C.40° D.45°
9.(2023·烟台芝罘区期末)如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为(A)
A.1 B.2 C.4 D.
10.如图,已知:在 ABCD中,E,F分别是AD,BC边的中点,G,H是对角线BD上的两点,且BG=DH,则下列结论中错误的是(A)
A.GF⊥FH B.GF=EH C.EF与AC互相平分 D.EG=FH
1.C ∵四边形ABCD是平行四边形,∠BAC=40°,
∴AB∥CD,
∴∠ACD=∠BAC=40°,
∵∠ACB=80°,
∴∠BCD=∠ACB+∠ACD=120°.
2.B 设这个多边形的边数是n,
由题意得(n-2)·180°=1 440°,
∴n=10.
3.D ∵多边形从一个顶点出发可引出2条对角线,
∴n-3=2,解得n=5.
∴内角和=(5-2)·180°=540°.
4.D A.80°+110°≠180°,故A选项不符合题意;
B.只有一组对边平行不能确定是平行四边形,故B选项不符合题意;
C.不能判断出任何一组对边是平行的,故C选项不符合题意;
D.有一组对边平行且相等是平行四边形,故D选项符合题意.
5.A 过点B作BH⊥AD于H,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EF⊥AD,BH⊥AD,∴BH∥EF,
∴四边形BHEF是平行四边形,
∵∠BHE=90°,
∴四边形BHEF为矩形,
∴HE=BF=3,EF=BH=8,
∵AE=9,
∴AH=AE-HE=9-3=6,
∴AB===10.
6.A ∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD.
∵BP是平行四边形BEPH的对角线,
∴S△BEP=S△BHP,
∵PD是平行四边形GPFD的对角线,
∴S△GPD=S△FPD.
∴S△ABD-S△BEP-S△GPD=S△BCD-S△BHP-S△PFD,
即S AEPG=S HCFP,
∴S ABHG=S BCFE,
同理S AEFD=S HCDG.
即S ABHG=S BCFE,S AEPG=S HCFP,S AEFD=S HCDG,
所以面积相等的平行四边形有3对.
7.D ∵四边形ABCD是平行四边形,
∴BC=AD,
∵点A的坐标为(-1,0),点B的坐标为(0,-2),点D的坐标为(2,0),
∴AD=BC=3,OB=2,∴C(3,-2),
∵将 ABCD平移,使点A(-1,0)移动到点A'(-2,1)处,
∴平移后C点的对应点C'的坐标为(2,-1).
8.B ∵∠1,∠2,∠3,∠4的邻补角的角度和为215°,
∴∠1+∠2+∠3+∠4+215°=4×180°,
∴∠1+∠2+∠3+∠4=505°,
∵五边形OAGFE内角和=(5-2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°-505°=35°.
9.A 延长CF交AB于G,
∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC=4,FG=CF,
∴BG=AB-AG=6-4=2.
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴EF=BG=1.
10.A 连接EF交BD于点O,
在平行四边形ABCD中,AD=BC,AD∥BC,∠EDH=∠FBG,
∵E,F分别是AD,BC边的中点,
∴DE=BF=BC,AE=BF,
∴四边形DEBF是平行四边形,四边形AEFB是平行四边形.
∴EF∥AB.
∵点E是AD的中点,∴点O是BD的中点.
根据平行四边形的对角线互相平分,故点O是AC的中点,也是EF的中点,故C不符合题意.
又∵BG=DH,∠EDH=∠FBG,DE=BF,
∴△DEH≌△BFG,
∴GF=EH,故B不符合题意.
∵∠DHE=∠BGF,
∴∠GHE=∠HGF.
又∵HG=GH,EH=FG,
∴△EHG≌△FGH,
∴EG=HF,故D不符合题意.
GF=EH,EG=HF,∴四边形EHFG是平行四边形,而不是矩形,故∠GFH不是90°,
∴A符合题意.
二、填空题(每小题4分,共20分)
11.(2022·南充中考)数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC,BC两边中点的距离DE为10 m(如图),则A,B两点的距离是 20 m.
12.如图,将△ABC沿它的中位线MN折叠后,点A落在点A'处,若∠A=30°,∠B=115°,则∠A'NC= 110 °.
13.如图,在正六边形ABCDEF中,AE与DF交于点O,则∠1的度数为 120° .
14.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF= .
15.如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且∠D>90°>∠C,则∠C= 72°或 .
11.【解析】∵CD=AD,CE=EB,
∴DE是△ABC的中位线,∴AB=2DE,
∵DE=10 m,∴AB=20 m.
答案:20
12.【解析】∵∠A=30°,∠B=115°,
∴∠C=180°-∠A-∠B=180°-30°-115°=35°,
∵MN是三角形的中位线,∴MN∥BC,
∴∠A'NM=∠ANM=∠C=35°,
∴∠A'NC=180°-∠ANM-∠A'NM=180°-35°-35°=110°.
答案:110
13.【解析】∵六边形ABCDEF是正六边形,
∴∠AFE=∠DEF=120°,AF=EF=DE,
∴∠FAE=∠FEA=∠EFD=(180°-120°)÷2=30°,
∴∠AFD=120°-30°=90°,
∴∠1=∠FAE+∠AFD=30°+90°=120°.
答案:120°
14.【解析】取BF的中点H,连接DH,
∵BD=DC,BH=HF,
∴DH=FC,DH∥AC,
∴∠HDE=∠FAE,
在△AEF和△DEH中,,
∴△AEF≌△DEH(ASA),
∴AF=DH,
∴AF=FC,
∵AC=4,
∴AF=.
答案:
15.【解析】由题意可知:AD=DE,
∴∠DAE=∠DEA,设∠DAE=∠DEA=x,
∵四边形ABCD是平行四边形,
∴CD∥AB,∠C=∠DAB,
∴∠DEA=∠EAB=x,
∴∠C=∠DAB=2x,
①AE=AB时,若BE=BC,
则有∠BEC=∠C,即(180°-x)=2x,
解得x=36°,
∴∠C=72°,
若EC=EB,则有∠EBC=∠C=2x,
∵∠DAB+∠ABC=180°,
∴4x+(180°-x)=180°,
解得x=,
∴∠C=,
②EA=EB时,同法可得∠C=72°,
综上所述,∠C=72°或.
答案:72°或
三、解答题(共90分)
16.(10分)如图,五边形ABCDE的内角都相等,EF平分∠AED,求证:EF⊥BC.
【证明】五边形的内角和为(5-2)×180°=540°,
∵5个内角都相等,
∴∠A=∠B=∠AED==108°,
∵EF平分∠AED,
∴∠1=∠2=54°,
∵四边形的内角和为360°,在四边形ABFE中,∠3=360°-(108°+108°+54°)=90°.
∴EF⊥BC.
17.(10分)(2022·梧州中考)如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
【证明】∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,
∵BE=DH,∴AB-BE=CD-DH,
即AE=CH,
在△AEF和△CHG中,,
∴△AEF≌△CHG(SAS),
∴EF=HG.
18.(10分)如图,已知AD∥BC,DE∥BF,点A,E,F,C在同一直线上且AF=CE.求证:四边形DEBF是平行四边形.
【证明】∵AD∥BC,DE∥BF,
∴∠A=∠C,∠DEF=∠BFE,
∴∠DEA=∠BFC,
∵AF=CE,
∴AF-EF=CE-EF,
∴AE=CF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴DE=BF,
∵DE∥BF,∴四边形DEBF是平行四边形.
19.(10分)已知:如图,在四边形ABCD中,∠BAC=∠ACD=90°,AB=CD,点E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=4,AD=4,求四边形ABCE的面积.
【解析】(1)∵∠BAC=∠ACD=90°,∴AB∥EC.
∵点E是CD的中点,∴EC=CD.
∵AB=CD,∴AB=EC.
∴四边形ABCE是平行四边形.
(2)∵∠ACD=90°,AC=4,AD=4,
∴CD==4.
∵AB=CD,∴AB=2.
∴S平行四边形ABCE=AB·AC=2×4=8.
20.(12分)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)证明:AC=EF;
(2)求证:四边形ADFE是平行四边形.
【证明】(1)∵在Rt△ABC中,∠BAC=30°,∴AB=2BC.
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.
在Rt△AFE和Rt△BCA中,
∴Rt△AFE≌Rt△BCA(HL).∴AC=EF.
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD.
∴∠DAB=∠DAC+∠BAC=90°.
又∵EF⊥AB,∴EF∥AD.
∵AC=EF,AC=AD,∴EF=AD.∴四边形ADFE是平行四边形.
21.(12分)(2023·烟台招远市期末)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接AF,FG,H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
【解析】(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∵BF=BE,CG=CE,∴BC是△EFG的中位线,
∴BC∥FG,BC=FG,
∵H为FG的中点,∴FH=FG,
∴BC∥FH,BC=FH,∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(2)∵∠BAE=80°,∴∠BCD=80°,
∵∠DCE=30°,∴∠BCE=80°-30°=50°,
∵CB=CE,∴∠CBE=∠CEB=(180°-50°)=65°.
22.(13分)如图,矩形ABCD中,AB=4 cm,BC=8 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以
1 cm/s的速度运动,设运动时间为t s.
(1)若动点M,N同时出发,t秒时,N走过_________cm,M走过_________cm;
(2)若动点M,N同时出发,经过几秒钟两点第一次相遇
(3)若点E在线段BC上,且BE=3 cm,若动点M,N同时出发,相遇时停止运动,经过几秒钟,点A,E,M,N组成平行四边形
【解析】(1)路程=时间×速度,时间为t,N的速度为1 cm/s,所以其路程为t,M的速度为2 cm/s,所以其路程为2t;
答案:t 2t
(2)根据题意得t+2t=2×(4+8)=24,
解得t=8,
即经过8秒钟两点第一次相遇;
(3)①如图1,点M在BC上且在E点右侧时,当AN=ME时,四边形AEMN为平行四边形,
得8-t=9-2t,
解得t=1,
此时点M在DC上,所以舍去;
②如图2,点M在BC上且在E点左侧时,当AN=ME时,四边形AMEN为平行四边形,
得8-t=2t-9,
解得t=,符合题意,
所以经过秒钟,点A,E,M,N组成平行四边形.
23. (13分)(2022·沈阳质检)如图,点B是∠MAN的边AM上的定点,点C是边AN上的动点,将△ABC绕点B逆时针旋转得到△DBE,且点A的对应点D恰好落在边AN上,连接CE.当BC=AC时.
(1)求证:四边形ABEC是平行四边形;
(2)若AB=15,AD=18,求AC的长.
【解析】(1)∵BC=AC,∴∠A=∠ABC.
∴∠BCD=∠A+∠ABC=2∠A.
∵△ABC绕点B逆时针旋转得到△DBE,
∴AB=BD,BC=BE,∠ABD=∠CBE.
∴∠BDA=∠A,∠BCE=∠BEC.∴∠A=∠BCE.
∵∠BCD=∠BCE+∠ECD,∴∠ECD=∠A=∠BEC.
∴AB∥CE,AC∥BE,∴四边形ABEC是平行四边形.
(2) 如图,过点B作BH⊥AD,垂足为H,
∵BD=BA,BH⊥AD,∴AH=AD=9.在Rt△ABH中,由勾股定理得,
BH===12.
设AC=BC=x,则CH=x-9.
在Rt△HCB中,由勾股定理得,(x-9)2+122=x2,
解得x=,即AC的长为.
