第1章 有理数 单元练习(含解析) 2023-2024学年上学期人教版数学七年级上册(山东地区适用)
文档属性
| 名称 | 第1章 有理数 单元练习(含解析) 2023-2024学年上学期人教版数学七年级上册(山东地区适用) |  | |
| 格式 | docx | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 13:42:09 | ||
图片预览




文档简介
第1章 有理数 单元练习
一、单选题
1.(2023上·山东德州·七年级统考期末)某中学进行立定跳远测试,男生成绩合格标准定为1.85米,体育老师记录了甲、乙、丙、丁四位男生成绩如下表:(超出标准的部分记为“+”,不足标准的部分记为“-”),你认为立定跳远成绩最好的是( )
学生 甲 乙 丙 丁
成绩/米
A.甲 B.乙 C.丙 D.丁
2.(2023上·山东济南·七年级统考期末)下面四个数中,负数是( )
A.0 B. C.1 D.
3.(2023上·山东聊城·七年级校考期末)小明在写作业时不慎将一滴墨水滴在数轴上,根据如图的数值,判断墨迹盖住的整数共有( )个
A.11 B.9 C.10 D.8
4.(2023上·山东德州·七年级统考期末)点A,B在数轴上的位置如图所示,若点A,B表示的数分别为a,b,且满足,则下列一定是正数的为( )
A.a B. C.b D.
5.(2023上·山东滨州·七年级统考期末)若不为的有理数与互为相反数,同学们化简后得出了下列不同的结果:①;②;③;④.其中结果错误的个数为( )
A. B. C. D.
6.(2023上·山东临沂·七年级统考期末)在,,0,这4个数中绝对值最大的数是( )
A. B. C.0 D.
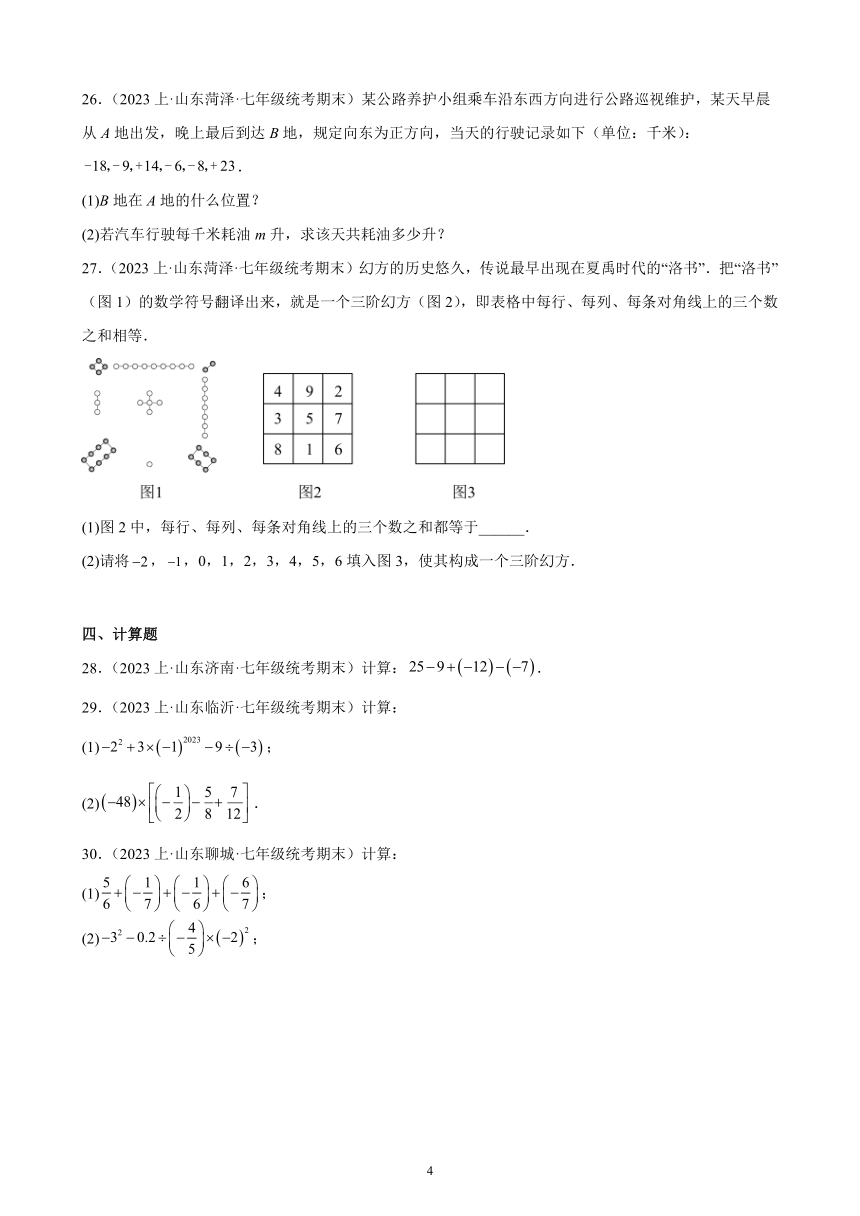
7.(2023上·山东临沂·七年级统考期末)如图,,两点在数轴上表示的数分别为,,下列结论正确的是( )
A. B. C. D.
8.(2023上·山东济宁·七年级统考期末)下列各数中是负数的是( )
A. B. C. D.
9.(2023上·山东滨州·七年级统考期末)下列各对数中,相等的一对是( )
A.与 B.与
C.与 D.与
10.(2023上·山东菏泽·七年级统考期末)国家疾控中心网站显示:截至2022年9月28日,全国累计报告接种新冠疫苗34亿3663万剂次,覆盖人数13亿万人,其中数据3663万用科学记数法表示为( )
A. B. C. D.
二、填空题
11.(2023上·山东济南·七年级统考期末)一个月内小明体重增加记为,小明体重减少应记为 .
12.(2023上·山东聊城·七年级统考期末) .(填“”“”或“”)
13.(2023上·山东菏泽·七年级统考期末)我们知道,表示在数轴上对应的点到原点的距离,我们可以把看作.所以,就表示与在数轴上对应的两点之间的距离.若,则 .
14.(2023上·山东滨州·七年级统考期末)我们知道,表示4与的差的绝对值,实际上也可理解为4与两数在数轴上所对应的两点之间的距离;同理也可理解为与3两数在数轴上所对应的两点之间的距离.若.则符合条件的整数的值 .
15.(2023上·山东临沂·七年级统考期末)如图的数轴上表示整数的点部分被墨迹盖住,那么被盖住的点表示整数的和为 .
16.(2023上·山东济宁·七年级统考期末)下列是运用有理数加法法则计算思考、计算过程的叙述:
①和2的绝对值分别为5和2;
②的绝对值5较大;2的绝对值2较小
③是异号两数相加;
④结果的绝对值是用得到;
⑤计算结果为;
⑥结果的符号是取的符号--负号;
请按运用法则思考、计算过程的先后顺序排序(只写序号): .
17.(2023上·山东济宁·七年级统考期末)绝对值小于的所有负整数的积是 .
18.(2023上·山东枣庄·七年级统考期末)的相反数是 ,倒数是 .
19.(2023上·山东滨州·七年级统考期末)已知,为有理数,如果规定一种新的运算“※”,规定:当时,※,当时,※,计算: .
20.(2023上·山东滨州·七年级统考期末)若是的倒数,则的相反数是 .
21.(2023上·山东滨州·七年级统考期末)某超市在元旦期间推出如下优惠方案:
(1)一次性购物不超过100元不享受优惠;
(2)一次性购物超过100元但不超过300元打九折;
(3)一次性购物超过300元一律打八五折.
元旦这天,小明和妈妈在该超市购物后分别自行付款70元和243元.如果小明和妈妈合作一次性付款,则应付款 元.
22.(2023上·山东菏泽·七年级统考期末)若,则 .
23.(2023上·山东菏泽·七年级统考期末)对于任意有理数,经过以下运算过程,当时,运算结果是 .
24.(2023上·山东菏泽·七年级统考期末)截至北京时间2022年10月1日,全国累计确诊新冠肺炎病例超过8200000例,将8200000用科学记数法表示为 .
三、问答题
25.(2022上·山东青岛·七年级校考期末)自己设计一个三阶幻方,填入表格中.
26.(2023上·山东菏泽·七年级统考期末)某公路养护小组乘车沿东西方向进行公路巡视维护,某天早晨从A地出发,晚上最后到达B地,规定向东为正方向,当天的行驶记录如下(单位:千米):
.
(1)B地在A地的什么位置?
(2)若汽车行驶每千米耗油m升,求该天共耗油多少升?
27.(2023上·山东菏泽·七年级统考期末)幻方的历史悠久,传说最早出现在夏禹时代的“洛书”.把“洛书”(图1)的数学符号翻译出来,就是一个三阶幻方(图2),即表格中每行、每列、每条对角线上的三个数之和相等.
(1)图2中,每行、每列、每条对角线上的三个数之和都等于______.
(2)请将,,0,1,2,3,4,5,6填入图3,使其构成一个三阶幻方.
四、计算题
28.(2023上·山东济南·七年级统考期末)计算:.
29.(2023上·山东临沂·七年级统考期末)计算:
(1);
(2).
30.(2023上·山东聊城·七年级统考期末)计算:
(1);
(2);
参考答案:
1.B
【分析】根据正负数的意义解答即可.
【详解】解:∵,
∴四位男同学成绩最好的是乙;
故选:B.
【点睛】本题考查学生对正数和负数的认识,弄清题意是解题的关键.
2.B
【分析】根据小于的数是负数即可求解.
【详解】解:A.既不是正数,也不是负数,故本选项不合题意;
B.是负数,故本选项符合题意;
C.1是正数,故本选项不合题意;
D.是正数,故本选项不合题意.
故选:.
【点睛】此题主要考查了正数和负数,判断一个数是正数还是负数,关键是看它比大还是比小.
3.B
【分析】根据题意结合数轴,知墨迹盖住的范围有两部分,即大于而小于,大于而小于,写出其中的整数即可.
【详解】解:结合数轴,得
墨迹盖住的整数共有,,,,,,,,共9个.
故选:B.
【点睛】本题考查数轴以及有理数,熟练掌握并弄清数轴上点表示的数是解答本题的关键.
4.C
【分析】根据数轴可知,再根据逐项判断即可.
【详解】解:由可知可能是负数,b是正数,故A不符合题意;
由可知b是正数,则一定为负数,故B不符合题意;
由可知b是正数,故C符合题意;
由可知可能是正数,则可能为负数,故D不符合题意;
故选:C.
【点睛】本题考查数轴,正数和负数,解题的关键是确定的正负.
5.C
【分析】根据互为相反的两个数的和是即可得到正确选项.
【详解】解:∵不为的有理数与互为相反数,
∴,
∴①②③错误,④正确;
故选.
【点睛】本题考查了相反数的定义和性质,熟记相反数的性质以及定义是解题的关键.
6.B
【分析】计算绝对值要根据绝对值的定义分别求出这四个数的绝对值,再进行比较即可.
【详解】解:,,,,
∵,
∴绝对值最大的数为,
故选:B.
【点睛】本题考查的是绝对值,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数, 0的绝对值是0.
7.C
【分析】根据数轴判断出,,再由有理数加(减)法法则、有理数的大小比较方法、与的符号,进行逐一判断即可.
【详解】解:由数轴得:,,
A. ,故此项错误;
B.因为,所以,故此项错误;
C.由数轴得到原点的距离小于到原点的距离,所以 ,故此项正确;
D.因为,,所以,故此项错误.
故选:C.
【点睛】本题考查了有理数的大小比较、有理数加(减)法、有理数的乘法法则,掌握相关的方法和法则是解题的关键.
8.C
【分析】根据绝对值的性质和有理数乘方的法则进行判断即可.
【详解】解:A.,不符合题意;
B.,不符合题意;
C.,符合题意;
D.,不符合题意,
故选:C.
【点睛】本题考查了绝对值的性质和有理数的乘方,熟练掌握有理数乘方的法则是解题的关键.
9.B
【分析】根据有理数的乘方运算,以及化简多重符号,化简绝对值进行计算即可求解.
【详解】解:A. ,,故该选项不符合题意;
B. ,,故该选项符合题意;
C.,,故该选项不符合题意;
D.,,故该选项不符合题意.
故选:B.
【点睛】本题考查了有理数的乘方运算,以及化简多重符号,化简绝对值,正确的计算是解题的关键.
10.A
【分析】科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【详解】解:万,
故选:A.
【点睛】此题考查了用科学记数法的表示数;科学记数法的表示形式为的形式,其中,为整数,解题的关键要正确确定的值以及的值.
11.
【分析】根据相反意义的量求解即可.
【详解】解:小明体重增加记为,
∴小明体重减少应记为,
故答案为:.
【点睛】题目主要考查正负数的应用及相反意义的量,理解题意是解题关键.
12.
【分析】利用有理数的比较大小解题即可.
【详解】解:根据正数大于一切负数可得,
故答案为:.
【点睛】本题考查有理数的比较大小,掌握正数大于负数是解题的关键.
13.或2
【分析】根据绝对值的意义,即可解答.
【详解】解:,
数轴上表示数的点到表示数的点的距离为5,
的值为或2.
故答案为:或2.
【点睛】本题主要考查了数轴及绝对值,熟练掌握数轴及绝对值的几何意义进行求解是解决本题的关键.
14.
【分析】根据题意可得表示与1的距离和与的距离之和为4,即可求解.
【详解】解:∵表示与1两数在数轴上所对应的两点之间的距离,
表示与两数在数轴上所对应的两点之间的距离,
∴表示与1的距离和与的距离之和为4,
∴,
∴符合条件的整数的值有:;
故答案为:.
【点睛】本题主要考查了绝对值和数轴,解题关键是正确理解题意,掌握绝对值的几何意义.
15.1
【分析】先求被盖住的整数,再求它们的和.
【详解】解:被盖住的点表示整数有:,,,1,2,3,4,
,
故答案为:1.
【点睛】本题考查了数轴,有理数的加法运算,求出相应整数是解题的关键.
16.③①②④⑥⑤或③①②⑥④⑤
【分析】根据有理数的加法法则,按照有理数加法法则的计算顺序逐个判断即可.
【详解】解:根据有理数加法法则:
应该先看两数符号是否相同,故应先③,
若符号不同,再看两数的绝对值,故再①,
然后再比较绝对值的大小,故再②,
然后再确定结果的绝对值与结果的符号,故再④⑥或⑥④;
最后得出结果,故最后为⑤;
综上分析可知,计算过程的先后顺序排序为③①②④⑥⑤或③①②⑥④⑤.
故答案为:③①②④⑥⑤或③①②⑥④⑤.
【点睛】本题考查有理数的加法法则,熟练掌握并理解加法法则的含义是解题的关键.
17.2
【分析】先求出绝对值小于的所有负整数,然后根据有理数的乘法计算法则求出它们的积即可.
【详解】解:由题意得,绝对值小于的负整数有,,
∴绝对值小于的所有负整数的积是,
故答案为:2.
【点睛】本题主要考查了有理数乘法计算,绝对值的意义,正确得到绝对值小于的负整数有,是解题的关键.
18.
【分析】先根据绝对值的意义求出,再根据只有符号不同的两个数互为相反数,乘积为1的两个数互为倒数进行求解即可.
【详解】,
的相反数是,倒数是,
故答案为:,.
【点睛】本题考查了化简绝对值,相反数和倒数的定义,熟练掌握知识点是解题的关键.
19.
【分析】根据新定义,先计算和,再相减即可.
【详解】∵,,
∴,,
∴,
故答案为.
【点睛】本题考查了新定义下的有理数的混合运算,正确理解题目所给运算法则是解题的关键.
20.
【分析】根据倒数的定义(两个数的积等于1,这两个数互为倒数)得出的值,根据相反数的定义(绝对值相等,符号不同)得出答案.
【详解】解:根据倒数的定义得:,
解得,
根据相反数的定义,的相反数是,
故答案为:.
【点睛】本题主要考查了倒数和相反数的定义,熟记相关定义是解答本题的关键.
21.289
【分析】首先计算出两次购买应该付款的数额,然后根据优惠方案即可求解.
【详解】解:∵,,
∴小明所购买的商品原价即为70元,妈妈所购买的商品按原价打九折计算,
∴妈妈所购买的商品的原价为元,
∴此时小明和妈妈购买的商品的总价为元>300元,
∴此时小明和妈妈合作一次性付款,则应付款元.
故答案为:289.
【点睛】本题考查了打折销售的运用,有理数运算的应用.正确求出商品原价是解答本题的关键.
22.
【分析】讨论:当时,根据绝对值的意义得到,解得,然后计算;当时,,无解.
【详解】解:当时,,
解得,
∴;
当时,,无解,
所以.
故答案为:.
【点睛】本题考查了绝对值:若,则;若,则;若,则.也考查了乘方.
23.3
【分析】直接代入数值计算即可.
【详解】解:将代入得:
,
,
.
故答案为:3.
【点睛】本题考查了有理数的混合运算,看明白图示所表示的运算顺序是解答本题的关键.
24.
【分析】科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
【详解】解:,
故答案为:.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为,表示时关键要正确确定的值以及的值.
25.见解析
【分析】根据题中的要求每一行、每一竖列及两条对角线上的数字的和都相等,填表即可.
【详解】解:如图所示
【点睛】本题考查了有理数的加法,熟练掌握运算法则是解题的关键.
26.(1)地在A地的西方,它们相距4千米.
(2)78.
【分析】(1)首先把当天的行驶记录数据相加,然后根据结果的正负即可确定B地在A地何方,相距多少千米;
(2)把所给的数据的绝对值相加,然后乘以m即可得到结果.
【详解】(1)解:根据题意,可得
答:地在A地的西方,它们相距4千米;
(2)根据题意,汽车共行驶了
(千米)
(升)
答:该天共耗油升.
【点睛】此题考查了正负数的意义,有理数加法的应用,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
27.(1)15
(2)见详解(答案不唯一)
【分析】(1)根据图中数据即可作答;
(2)先将已知的9个数求和,再除以3即可求出每行、每列、每条对角线上的三个数之和,根据幻方的特点可知,已知的从小到大的排列的9个数中,居于中间位置的数填在幻方的正中心的格子中,并且这列数中最大的数与最小的数必在一起,据此填表即可.
【详解】(1)任取两组数据,由图2可知:,
故答案为:15;
(2),
即幻方中,每行、每列、每条对角线上的三个数之和都等于6,
根据幻方的特点可知:从小到大的排列的9个数中,居于中间位置的数填在幻方的正中心的格子中,并且这列数中最大的数与最小的数必在一起,
即三阶幻方如下:
(答案不唯一)
【点睛】本题主要考查了有理数的加减乘除运算,掌握有理数的加减乘除运算法则,是解答本题的关键.
28.11
【分析】应用有理数加减混合运算法则进行计算即可得出答案.
【详解】解:原式
【点睛】本题主要考查了有理数的加减混合运算,熟练掌握有理数混合运算法则进行求解是解决本题的关键.
29.(1)
(2)
【分析】(1)先计算有理数的乘方,再根据有理数的混合运算法则计算即可;
(2)根据乘法分配律计算即可.
【详解】(1)解:
;
(2)
.
【点睛】本题考查了有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和法则.
30.(1)
(2)
【分析】(1)根据有理数的加减法即可求解;
(2)先算乘方,再算乘除法,最后算加减,即可求解.
【详解】(1)解:原式;
(2)原式.
【点睛】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
一、单选题
1.(2023上·山东德州·七年级统考期末)某中学进行立定跳远测试,男生成绩合格标准定为1.85米,体育老师记录了甲、乙、丙、丁四位男生成绩如下表:(超出标准的部分记为“+”,不足标准的部分记为“-”),你认为立定跳远成绩最好的是( )
学生 甲 乙 丙 丁
成绩/米
A.甲 B.乙 C.丙 D.丁
2.(2023上·山东济南·七年级统考期末)下面四个数中,负数是( )
A.0 B. C.1 D.
3.(2023上·山东聊城·七年级校考期末)小明在写作业时不慎将一滴墨水滴在数轴上,根据如图的数值,判断墨迹盖住的整数共有( )个
A.11 B.9 C.10 D.8
4.(2023上·山东德州·七年级统考期末)点A,B在数轴上的位置如图所示,若点A,B表示的数分别为a,b,且满足,则下列一定是正数的为( )
A.a B. C.b D.
5.(2023上·山东滨州·七年级统考期末)若不为的有理数与互为相反数,同学们化简后得出了下列不同的结果:①;②;③;④.其中结果错误的个数为( )
A. B. C. D.
6.(2023上·山东临沂·七年级统考期末)在,,0,这4个数中绝对值最大的数是( )
A. B. C.0 D.
7.(2023上·山东临沂·七年级统考期末)如图,,两点在数轴上表示的数分别为,,下列结论正确的是( )
A. B. C. D.
8.(2023上·山东济宁·七年级统考期末)下列各数中是负数的是( )
A. B. C. D.
9.(2023上·山东滨州·七年级统考期末)下列各对数中,相等的一对是( )
A.与 B.与
C.与 D.与
10.(2023上·山东菏泽·七年级统考期末)国家疾控中心网站显示:截至2022年9月28日,全国累计报告接种新冠疫苗34亿3663万剂次,覆盖人数13亿万人,其中数据3663万用科学记数法表示为( )
A. B. C. D.
二、填空题
11.(2023上·山东济南·七年级统考期末)一个月内小明体重增加记为,小明体重减少应记为 .
12.(2023上·山东聊城·七年级统考期末) .(填“”“”或“”)
13.(2023上·山东菏泽·七年级统考期末)我们知道,表示在数轴上对应的点到原点的距离,我们可以把看作.所以,就表示与在数轴上对应的两点之间的距离.若,则 .
14.(2023上·山东滨州·七年级统考期末)我们知道,表示4与的差的绝对值,实际上也可理解为4与两数在数轴上所对应的两点之间的距离;同理也可理解为与3两数在数轴上所对应的两点之间的距离.若.则符合条件的整数的值 .
15.(2023上·山东临沂·七年级统考期末)如图的数轴上表示整数的点部分被墨迹盖住,那么被盖住的点表示整数的和为 .
16.(2023上·山东济宁·七年级统考期末)下列是运用有理数加法法则计算思考、计算过程的叙述:
①和2的绝对值分别为5和2;
②的绝对值5较大;2的绝对值2较小
③是异号两数相加;
④结果的绝对值是用得到;
⑤计算结果为;
⑥结果的符号是取的符号--负号;
请按运用法则思考、计算过程的先后顺序排序(只写序号): .
17.(2023上·山东济宁·七年级统考期末)绝对值小于的所有负整数的积是 .
18.(2023上·山东枣庄·七年级统考期末)的相反数是 ,倒数是 .
19.(2023上·山东滨州·七年级统考期末)已知,为有理数,如果规定一种新的运算“※”,规定:当时,※,当时,※,计算: .
20.(2023上·山东滨州·七年级统考期末)若是的倒数,则的相反数是 .
21.(2023上·山东滨州·七年级统考期末)某超市在元旦期间推出如下优惠方案:
(1)一次性购物不超过100元不享受优惠;
(2)一次性购物超过100元但不超过300元打九折;
(3)一次性购物超过300元一律打八五折.
元旦这天,小明和妈妈在该超市购物后分别自行付款70元和243元.如果小明和妈妈合作一次性付款,则应付款 元.
22.(2023上·山东菏泽·七年级统考期末)若,则 .
23.(2023上·山东菏泽·七年级统考期末)对于任意有理数,经过以下运算过程,当时,运算结果是 .
24.(2023上·山东菏泽·七年级统考期末)截至北京时间2022年10月1日,全国累计确诊新冠肺炎病例超过8200000例,将8200000用科学记数法表示为 .
三、问答题
25.(2022上·山东青岛·七年级校考期末)自己设计一个三阶幻方,填入表格中.
26.(2023上·山东菏泽·七年级统考期末)某公路养护小组乘车沿东西方向进行公路巡视维护,某天早晨从A地出发,晚上最后到达B地,规定向东为正方向,当天的行驶记录如下(单位:千米):
.
(1)B地在A地的什么位置?
(2)若汽车行驶每千米耗油m升,求该天共耗油多少升?
27.(2023上·山东菏泽·七年级统考期末)幻方的历史悠久,传说最早出现在夏禹时代的“洛书”.把“洛书”(图1)的数学符号翻译出来,就是一个三阶幻方(图2),即表格中每行、每列、每条对角线上的三个数之和相等.
(1)图2中,每行、每列、每条对角线上的三个数之和都等于______.
(2)请将,,0,1,2,3,4,5,6填入图3,使其构成一个三阶幻方.
四、计算题
28.(2023上·山东济南·七年级统考期末)计算:.
29.(2023上·山东临沂·七年级统考期末)计算:
(1);
(2).
30.(2023上·山东聊城·七年级统考期末)计算:
(1);
(2);
参考答案:
1.B
【分析】根据正负数的意义解答即可.
【详解】解:∵,
∴四位男同学成绩最好的是乙;
故选:B.
【点睛】本题考查学生对正数和负数的认识,弄清题意是解题的关键.
2.B
【分析】根据小于的数是负数即可求解.
【详解】解:A.既不是正数,也不是负数,故本选项不合题意;
B.是负数,故本选项符合题意;
C.1是正数,故本选项不合题意;
D.是正数,故本选项不合题意.
故选:.
【点睛】此题主要考查了正数和负数,判断一个数是正数还是负数,关键是看它比大还是比小.
3.B
【分析】根据题意结合数轴,知墨迹盖住的范围有两部分,即大于而小于,大于而小于,写出其中的整数即可.
【详解】解:结合数轴,得
墨迹盖住的整数共有,,,,,,,,共9个.
故选:B.
【点睛】本题考查数轴以及有理数,熟练掌握并弄清数轴上点表示的数是解答本题的关键.
4.C
【分析】根据数轴可知,再根据逐项判断即可.
【详解】解:由可知可能是负数,b是正数,故A不符合题意;
由可知b是正数,则一定为负数,故B不符合题意;
由可知b是正数,故C符合题意;
由可知可能是正数,则可能为负数,故D不符合题意;
故选:C.
【点睛】本题考查数轴,正数和负数,解题的关键是确定的正负.
5.C
【分析】根据互为相反的两个数的和是即可得到正确选项.
【详解】解:∵不为的有理数与互为相反数,
∴,
∴①②③错误,④正确;
故选.
【点睛】本题考查了相反数的定义和性质,熟记相反数的性质以及定义是解题的关键.
6.B
【分析】计算绝对值要根据绝对值的定义分别求出这四个数的绝对值,再进行比较即可.
【详解】解:,,,,
∵,
∴绝对值最大的数为,
故选:B.
【点睛】本题考查的是绝对值,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数, 0的绝对值是0.
7.C
【分析】根据数轴判断出,,再由有理数加(减)法法则、有理数的大小比较方法、与的符号,进行逐一判断即可.
【详解】解:由数轴得:,,
A. ,故此项错误;
B.因为,所以,故此项错误;
C.由数轴得到原点的距离小于到原点的距离,所以 ,故此项正确;
D.因为,,所以,故此项错误.
故选:C.
【点睛】本题考查了有理数的大小比较、有理数加(减)法、有理数的乘法法则,掌握相关的方法和法则是解题的关键.
8.C
【分析】根据绝对值的性质和有理数乘方的法则进行判断即可.
【详解】解:A.,不符合题意;
B.,不符合题意;
C.,符合题意;
D.,不符合题意,
故选:C.
【点睛】本题考查了绝对值的性质和有理数的乘方,熟练掌握有理数乘方的法则是解题的关键.
9.B
【分析】根据有理数的乘方运算,以及化简多重符号,化简绝对值进行计算即可求解.
【详解】解:A. ,,故该选项不符合题意;
B. ,,故该选项符合题意;
C.,,故该选项不符合题意;
D.,,故该选项不符合题意.
故选:B.
【点睛】本题考查了有理数的乘方运算,以及化简多重符号,化简绝对值,正确的计算是解题的关键.
10.A
【分析】科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【详解】解:万,
故选:A.
【点睛】此题考查了用科学记数法的表示数;科学记数法的表示形式为的形式,其中,为整数,解题的关键要正确确定的值以及的值.
11.
【分析】根据相反意义的量求解即可.
【详解】解:小明体重增加记为,
∴小明体重减少应记为,
故答案为:.
【点睛】题目主要考查正负数的应用及相反意义的量,理解题意是解题关键.
12.
【分析】利用有理数的比较大小解题即可.
【详解】解:根据正数大于一切负数可得,
故答案为:.
【点睛】本题考查有理数的比较大小,掌握正数大于负数是解题的关键.
13.或2
【分析】根据绝对值的意义,即可解答.
【详解】解:,
数轴上表示数的点到表示数的点的距离为5,
的值为或2.
故答案为:或2.
【点睛】本题主要考查了数轴及绝对值,熟练掌握数轴及绝对值的几何意义进行求解是解决本题的关键.
14.
【分析】根据题意可得表示与1的距离和与的距离之和为4,即可求解.
【详解】解:∵表示与1两数在数轴上所对应的两点之间的距离,
表示与两数在数轴上所对应的两点之间的距离,
∴表示与1的距离和与的距离之和为4,
∴,
∴符合条件的整数的值有:;
故答案为:.
【点睛】本题主要考查了绝对值和数轴,解题关键是正确理解题意,掌握绝对值的几何意义.
15.1
【分析】先求被盖住的整数,再求它们的和.
【详解】解:被盖住的点表示整数有:,,,1,2,3,4,
,
故答案为:1.
【点睛】本题考查了数轴,有理数的加法运算,求出相应整数是解题的关键.
16.③①②④⑥⑤或③①②⑥④⑤
【分析】根据有理数的加法法则,按照有理数加法法则的计算顺序逐个判断即可.
【详解】解:根据有理数加法法则:
应该先看两数符号是否相同,故应先③,
若符号不同,再看两数的绝对值,故再①,
然后再比较绝对值的大小,故再②,
然后再确定结果的绝对值与结果的符号,故再④⑥或⑥④;
最后得出结果,故最后为⑤;
综上分析可知,计算过程的先后顺序排序为③①②④⑥⑤或③①②⑥④⑤.
故答案为:③①②④⑥⑤或③①②⑥④⑤.
【点睛】本题考查有理数的加法法则,熟练掌握并理解加法法则的含义是解题的关键.
17.2
【分析】先求出绝对值小于的所有负整数,然后根据有理数的乘法计算法则求出它们的积即可.
【详解】解:由题意得,绝对值小于的负整数有,,
∴绝对值小于的所有负整数的积是,
故答案为:2.
【点睛】本题主要考查了有理数乘法计算,绝对值的意义,正确得到绝对值小于的负整数有,是解题的关键.
18.
【分析】先根据绝对值的意义求出,再根据只有符号不同的两个数互为相反数,乘积为1的两个数互为倒数进行求解即可.
【详解】,
的相反数是,倒数是,
故答案为:,.
【点睛】本题考查了化简绝对值,相反数和倒数的定义,熟练掌握知识点是解题的关键.
19.
【分析】根据新定义,先计算和,再相减即可.
【详解】∵,,
∴,,
∴,
故答案为.
【点睛】本题考查了新定义下的有理数的混合运算,正确理解题目所给运算法则是解题的关键.
20.
【分析】根据倒数的定义(两个数的积等于1,这两个数互为倒数)得出的值,根据相反数的定义(绝对值相等,符号不同)得出答案.
【详解】解:根据倒数的定义得:,
解得,
根据相反数的定义,的相反数是,
故答案为:.
【点睛】本题主要考查了倒数和相反数的定义,熟记相关定义是解答本题的关键.
21.289
【分析】首先计算出两次购买应该付款的数额,然后根据优惠方案即可求解.
【详解】解:∵,,
∴小明所购买的商品原价即为70元,妈妈所购买的商品按原价打九折计算,
∴妈妈所购买的商品的原价为元,
∴此时小明和妈妈购买的商品的总价为元>300元,
∴此时小明和妈妈合作一次性付款,则应付款元.
故答案为:289.
【点睛】本题考查了打折销售的运用,有理数运算的应用.正确求出商品原价是解答本题的关键.
22.
【分析】讨论:当时,根据绝对值的意义得到,解得,然后计算;当时,,无解.
【详解】解:当时,,
解得,
∴;
当时,,无解,
所以.
故答案为:.
【点睛】本题考查了绝对值:若,则;若,则;若,则.也考查了乘方.
23.3
【分析】直接代入数值计算即可.
【详解】解:将代入得:
,
,
.
故答案为:3.
【点睛】本题考查了有理数的混合运算,看明白图示所表示的运算顺序是解答本题的关键.
24.
【分析】科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
【详解】解:,
故答案为:.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为,表示时关键要正确确定的值以及的值.
25.见解析
【分析】根据题中的要求每一行、每一竖列及两条对角线上的数字的和都相等,填表即可.
【详解】解:如图所示
【点睛】本题考查了有理数的加法,熟练掌握运算法则是解题的关键.
26.(1)地在A地的西方,它们相距4千米.
(2)78.
【分析】(1)首先把当天的行驶记录数据相加,然后根据结果的正负即可确定B地在A地何方,相距多少千米;
(2)把所给的数据的绝对值相加,然后乘以m即可得到结果.
【详解】(1)解:根据题意,可得
答:地在A地的西方,它们相距4千米;
(2)根据题意,汽车共行驶了
(千米)
(升)
答:该天共耗油升.
【点睛】此题考查了正负数的意义,有理数加法的应用,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
27.(1)15
(2)见详解(答案不唯一)
【分析】(1)根据图中数据即可作答;
(2)先将已知的9个数求和,再除以3即可求出每行、每列、每条对角线上的三个数之和,根据幻方的特点可知,已知的从小到大的排列的9个数中,居于中间位置的数填在幻方的正中心的格子中,并且这列数中最大的数与最小的数必在一起,据此填表即可.
【详解】(1)任取两组数据,由图2可知:,
故答案为:15;
(2),
即幻方中,每行、每列、每条对角线上的三个数之和都等于6,
根据幻方的特点可知:从小到大的排列的9个数中,居于中间位置的数填在幻方的正中心的格子中,并且这列数中最大的数与最小的数必在一起,
即三阶幻方如下:
(答案不唯一)
【点睛】本题主要考查了有理数的加减乘除运算,掌握有理数的加减乘除运算法则,是解答本题的关键.
28.11
【分析】应用有理数加减混合运算法则进行计算即可得出答案.
【详解】解:原式
【点睛】本题主要考查了有理数的加减混合运算,熟练掌握有理数混合运算法则进行求解是解决本题的关键.
29.(1)
(2)
【分析】(1)先计算有理数的乘方,再根据有理数的混合运算法则计算即可;
(2)根据乘法分配律计算即可.
【详解】(1)解:
;
(2)
.
【点睛】本题考查了有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和法则.
30.(1)
(2)
【分析】(1)根据有理数的加减法即可求解;
(2)先算乘方,再算乘除法,最后算加减,即可求解.
【详解】(1)解:原式;
(2)原式.
【点睛】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
