第4章 几何图形初步 单元练习(含解析) 2023-2024学年上学期人教版数学七年级上册(山东地区适用)
文档属性
| 名称 | 第4章 几何图形初步 单元练习(含解析) 2023-2024学年上学期人教版数学七年级上册(山东地区适用) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 14:18:17 | ||
图片预览




文档简介
第4章 几何图形初步 单元练习
一、单选题
1.(2023上·山东临沂·七年级统考期末)如图,正方体的6个面上分别标有汉字“河”“东”“初”“中”“数”“学”,将该正方体按图示方式转动,根据图形可得与“学”相对的是( )
A.河 B.东 C.初 D.数
2.(2023上·山东济南·七年级统考期末)下列几何体中,从左面看得到的图是三角形的是( )
A. B.
C. D.
3.(2022上·山东威海·七年级统考期末)如图,将一张正方形纸片沿对角线折叠一次,得到一个三角形.在得到的三角形的三个内角各剪去一个圆,然后将纸片展开,得到的图案是( )
A. B.
C. D.
4.(2023上·山东滨州·七年级统考期末)由如图的正方体平面展开图可知,此正方体的“绿”字所在面的对面汉字是( )
A.低 B.碳 C.发 D.展
5.(2023上·山东济南·七年级统考期末)如图是一个正方体的表面展开图,这个正方体相对表面上所标的数字相等,则的值为( )
A. B.-1 C.0 D.4
6.(2023上·山东德州·七年级校考期末)如下图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和五边形,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图是( )
A. B. C. D.
7.(2023上·山东临沂·七年级统考期末)中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
8.(2023上·山东济南·七年级统考期末)卡塔尔世界杯已降下帷幕.为了筹办本届世界杯,卡塔尔耗资建造了座各具特色的球场.如图,阿图玛玛体育场位于多哈西南部,形状类似于圆柱体,外墙带有丰富的花边状装饰.下列图形绕虚线旋转一周,能形成圆柱体的是( )
A. B. C. D.
9.(2023上·山东菏泽·七年级统考期末)有下列生活、生产现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定同一行两棵树的位置,就能确定这行树所在的直线;④在正常条件下射击,要保证目标在准星和缺口确定的直线上,才能射中目标.其中能用“两点确定一条直线”来解释的现象有( )
A.①② B.①③ C.①④ D.①③④
10.(2023上·山东枣庄·七年级统考期末)在直线上取A,B,C三点,使得,如果O是线段的中点,那么线段的长为( )
A. B. C.或 D.以上结论都不对
11.(2023上·山东临沂·七年级统考期末)下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段的长度叫两点的距离;
③两点之间线段最短;
④如果,则点B是的中点;
⑤直线经过点A,那么点A在直线上.
A.2个 B.3个 C.4个 D.5个
12.(2023上·山东临沂·七年级统考期末)如图,学校在蕾蕾家南偏西的方向上,点表示超市所在的位置,,则超市在蕾蕾家的( )
A.北偏东的方向上 B.南偏东的方向上
C.北偏东的方向上 D.南偏东的方向上
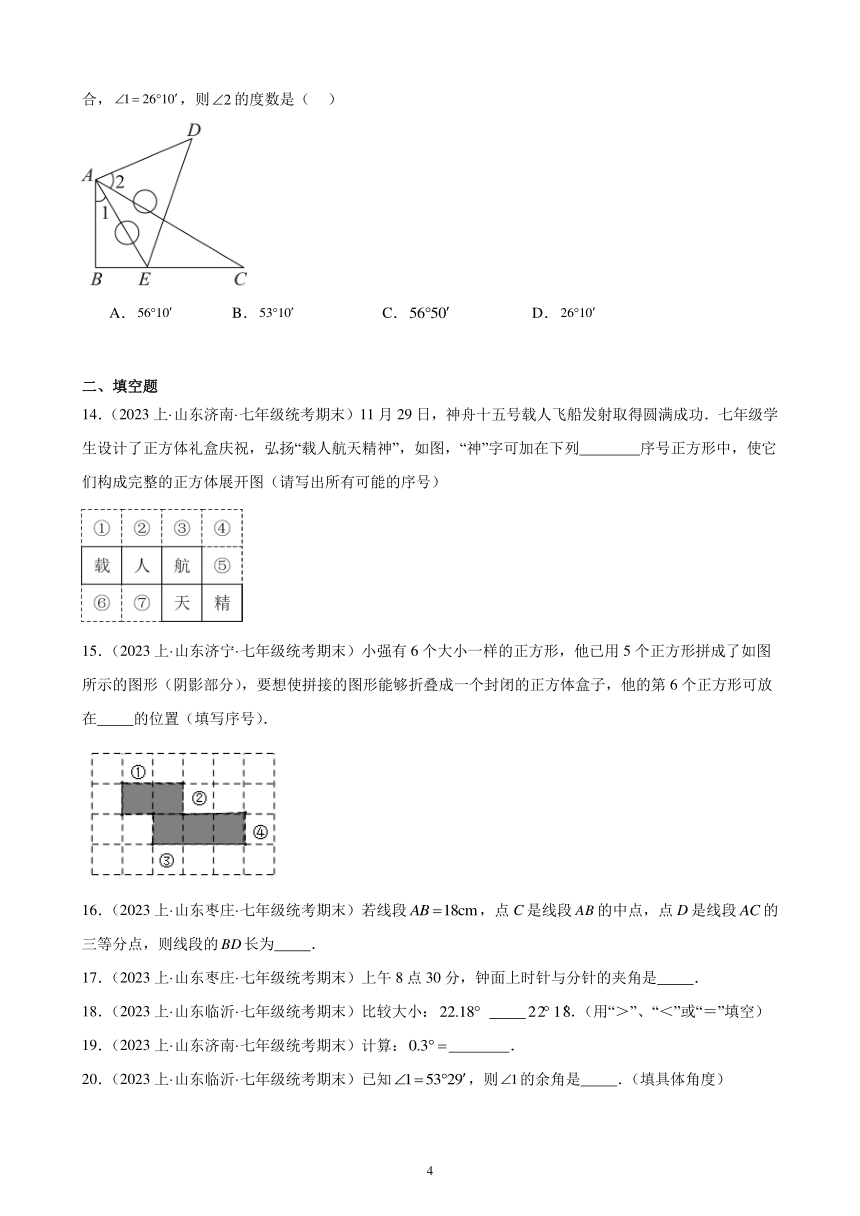
13.(2023上·山东临沂·七年级统考期末)如图,将一个三角板角的顶点与另一个三角板的直角顶点重合,,则的度数是( )
A. B. C. D.
二、填空题
14.(2023上·山东济南·七年级统考期末)11月29日,神舟十五号载人飞船发射取得圆满成功.七年级学生设计了正方体礼盒庆祝,弘扬“载人航天精神”,如图,“神”字可加在下列 序号正方形中,使它们构成完整的正方体展开图(请写出所有可能的序号)
15.(2023上·山东济宁·七年级统考期末)小强有6个大小一样的正方形,他已用5个正方形拼成了如图所示的图形(阴影部分),要想使拼接的图形能够折叠成一个封闭的正方体盒子,他的第6个正方形可放在 的位置(填写序号).
16.(2023上·山东枣庄·七年级统考期末)若线段,点C是线段的中点,点D是线段的三等分点,则线段的长为 .
17.(2023上·山东枣庄·七年级统考期末)上午8点30分,钟面上时针与分针的夹角是 .
18.(2023上·山东临沂·七年级统考期末)比较大小: .(用“>”、“<”或“=”填空)
19.(2023上·山东济南·七年级统考期末)计算: .
20.(2023上·山东临沂·七年级统考期末)已知,则的余角是 .(填具体角度)
三、问答题
21.(2023上·山东菏泽·七年级统考期末)如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)在图①中,画线段交于E点;
(2)在图①中作射线;
(3)在图②中取一点P,使点P既在直线上又在直线上.
22.(2023上·山东济宁·七年级统考期末)A、B、C、D四个车站的位置如图所示,A、B两站之间的距离,B、C两站之间的距离,B、D两站之间的距离.若A、C两站之间的距离,求C、D两站之间的距离.
23.(2023上·山东滨州·七年级统考期末)如图所示,射线的方向是北偏东,射线的方向是东偏北,若平分,则射线的方向是北偏西多少度?
24.(2023上·山东滨州·七年级统考期末)已知,在内部作射线,使得.
(1)如图,在内部作射线,使得;作射线平分,求的度数;
(2)如果过点作射线,使得,则的度数为______.(不需写演推过程)
25.(2023上·山东临沂·七年级统考期末)已知是直线上的一点,是直角,平分.
(1)在图1中,若,求的度数;
(2)将图1中的绕顶点顺时针旋转至图2的位置,若,试用含的式子表示;
(3)继续旋转至图3的位置,若,其他条件不变,试将图形补充完整,则_____(用含的式子表示).
26.(2023上·山东济宁·七年级统考期末)如图,点,,在同一条直线上,平分,.平分吗?请说明理由.
四、作图题
27.(2023上·山东临沂·七年级统考期末)如图,、、是平面上三个点,按要求画出图形,并回答问题.
(1)作直线,射线,线段;
(2)请用适当的语句表述点与直线的关系:________;
(3)从点到点的所有线中,线段最短,其理论依据是________;
28.(2023上·山东济宁·七年级统考期末)如图,平面上不共线的三点A、B、C,请按如下要求作图:
(1)画直线;
(2)画射线;
(3)①延长线段AC至D,使;
②在①的条件下,若,则 .(直接写出答案)
29.(2023上·山东临沂·七年级统考期末)点A、B在数轴上所表示的数如图所示,P是数轴上一点:
(1)将点B在数轴上向左移动2个单位长度,再向右移动6个单位长度,得到点P,则A、P两点间的距离是______个单位长度.
(2)若点B在数轴上移动了m个单位长度到点P,且A、P两点间的距离是4,则______.
(3)若点M为的中点,点N为的中点,点P在运动过程中,线段的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段的长度.
30.(2023上·山东滨州·七年级统考期末)已知线段,延长到,使得,然后反向延长线段到,使得.
(1)请根据题意画出图形;
(2)若点为线段的中点,且,求的长.
五、计算题
31.(2022上·山东枣庄·七年级校考期末)如图,O为直线上一点,,平分.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出的度数;
(3)请通过计算说明是否平分.
参考答案:
1.C
【分析】根据题意,理解旋转过程中,各个面的变化情况.
【详解】由第一次旋转知,与“中”相对的是“数”,由第二次旋转知,与“学”相对是的“学”,
故选:C
【点睛】本题考查简单的几何体,具备一定的空间想象能力是解题的关键.
2.C
【分析】利用从左面看所得到的图形,进而分析得出即可.
【详解】解:A、从左面看得到的图是圆,不符合题意;
B、从左面看得到的图是圆,不符合题意;
C、从左面看得到的图三角形,符合题意;
D、从左面看得到的图等腰梯形,不符合题意;
故选:C.
【点睛】本题考查了从三个方向看物体的形状,掌握定义是关键.
3.A
【分析】由平面图形的折叠及立体图形的表面展开图的特点解结合实际操作解题.
【详解】解:在三角形的角上剪洞,展开后洞肯定还是在角上,排除C和D;
画出折叠线,两个三角形中每个三角形的角上都有一个洞,排除B;
所以答案为A;
故选:A.
【点睛】本题考查学生的空间想象能力和动手实践能力,熟练掌握空间想象能力是解题的关键.
4.C
【分析】根据正方体的表面展开图,相对的面之间一定相隔一个正方形,即可求解.
【详解】解:这是一个正方体的平面展开图,共有六个面,其中面“色”与面“碳”相对,面“绿”与面“发”相对,面“低”与面“展”相对.
故选:C
【点睛】本题主要考查了正方体的平面展开图的特征,熟练掌握正方体的表面展开图,相对的面之间一定相隔一个正方形是解题的关键.
5.A
【分析】根据题意可得先找出x和y的相对面,根据相对表面上所标的数字相等即可得到x和y的值,
【详解】解:由图可知:x的相对面是,y的相对面是,
∵相对表面上所标的数字相等,
∴,
∴,
故选:A.
【点睛】本题考查了正方体相对两个面上的文字,掌握找正方体相对两个面上的文字的方法,注意正方体的空间图形,从相对面入手,分析解答问题是解题的关键.
6.C
【分析】本题考查正方体的表面展开图及空间想象能力.在验证立方体的展开图时,要细心观察每一个标志的位置是否一致,然后进行判断.
【详解】解:把四个选项的展开图折叠,能复原的是C.
故选:C.
【点睛】本题考查了正方体的展开图,解决本题的关键是熟练掌握正方体的展开图,解决这类问题时,不妨动手实际操作一下,即可解决问题.
7.A
【分析】枪挑是用枪尖挑,枪尖可看作点,棍可看作线,转化成数学思想即可.
【详解】所以由题意可得:从数学的角度可解释为点动成线,线动成面.
故选:A.
【点睛】本题考查了点、线、面、体的知识点,熟练掌握点、线、面之间的关系是解题的关键.
8.C
【分析】根据选项中图形的特点,圆柱体的特点,进行对比即可求解.
【详解】解:.旋转后是圆台,不符题意;
.旋转后是球,不符题意;
.旋转后是圆柱体,符合题意;
.旋转后是圆锥,不符题意;
故选:.
【点睛】本题主要考查立体几何的平面图,结合立体图形的特点,平面图形的特点是解题的关键.
9.D
【分析】根据两点确定一条直线,两点之间线段最短的性质逐一对各选项进行判断即可得到答案.
【详解】解:①利用了两点确定一条直线的性质,符合题意;
②利用了两点之间线段最短的性质,不符合题意;
③利用了两点确定一条直线的性质,符合题意;
④利用了两点确定一条直线的性质,符合题意,
能用“两点确定一条直线”来解释的现象有①③④,
故选D.
【点睛】本题考查了线段的性质以及直线的性质,正确理解并熟记相关性质公理是解题关键,属于基础题.
10.C
【分析】分两种情况,即B在之间,C在之间,先求出的长度,再根据线段中点的定义求出的长度即可.
【详解】①如图,
∵,
∴,
∵O是线段的中点,
∴
②如图,
∵,
∴,
∵O是线段的中点,
∴
故选C.
【点睛】此题主要考查线段中点的定义和线段的和差,熟练掌握线段中点定义是解题关键.
11.C
【分析】根据点和直线的位置关系,直线的性质,线段的性质,两点之间的距离的定义逐个判断即可.
【详解】解:过两点有且只有一条直线,故①正确;
连接两点的线段的长度叫两点的距离,故②正确;
两点之间,线段最短,故③正确;
当在直线外时,,则点不是的中点,故④错误;
直线经过点,那么点在直线上,故⑤正确,
即正确的有4个,
故选:C.
【点睛】本题考查了点和直线的位置关系,直线的性质,线段的性质,两点之间的距离的定义的应用,能熟记知识点是解此题的关键.
12.D
【分析】直接利用方向角的定义得出的度数.
【详解】如图所示:
由题意可得: , ,
则 ,
故超市在蕾蕾家的南偏东 的方向上.
故选:D.
【点睛】本题考查了方向角的定义,解题的关键是正确根据图形得出的度数.
13.A
【分析】利用求出的度数,再用求出的度数.
【详解】解:由图可知:,
;
故选:A.
【点睛】本题考查三角板中角的计算.根据图形,理清角的和差关系,是解题的关键.
14.①②③
【分析】根据正方体表面展开图的特征即可得出答案.
【详解】解:“神”字可加在①②③的位置,
故答案为:①②③.
【点睛】本题考查正方体的展开图特点,掌握正方体表面展开图的特征是正确解题的关键.
15.③
【分析】根据正方体的表面展开图分析即可求解.
【详解】解:如图所示,
故答案为:③.
【点睛】本题考查了正方体的表面展开图,理正方体的表面展开图的模型是解题的关键.正方体的表面展开图用‘口诀’:一线不过四,田凹应弃之,相间、Z端是对面,间二、拐角邻面知.
16.或
【分析】根据线段中点的定义和线段三等分点的定义即可得到结论.
【详解】解:是线段的中点,,
,
点是线段的三等分点,
①当时,如图,
;
②当时,如图,
.
所以线段的长为或.
故答案为:或.
【点睛】本题考查了两点间的距离,线段中点的定义,分类讨论思想的运用是解题的关键.
17./度
【分析】根据分针每分钟转,时针每分钟转,结合钟面被分成12大格,每大格可计算出30分钟时针与分针所转的角度,所以此时钟面上时针与分针夹角的度数.
【详解】解:30分钟,钟面上时针从8开始转的度数为,
所以此时钟面上时针与分针夹角的度数.
故答案为:.
【点睛】本题考查了钟面角:掌握“钟面被分成12大格,每大格;分针每分钟转,时针每分钟转”是解本题的关键.
18.
【分析】先根据度分秒的换算,把和全化成秒,再比较大小即可.
【详解】解:∵
,
∴.
故答案为:.
【点睛】此题考查了度分秒的换算,关键是把和化成秒,转化时要注意单位统一.
19.
【分析】根据计算即可得出答案.
【详解】
故答案为:
【点睛】本题主要考查角的运算,熟记,是解题的关键.
20.
【分析】直接根据余角的定义即可求解.
【详解】解:∵,
∴的余角=,
故答案为:.
【点睛】本题考查了余角的定义,解题关键是掌握互余的两个角相加为.
21.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据线段的定义画图即可;
(2)以B为端点画射线即可;
(3)作直线和直线相交,交点即为点P.
【详解】(1)如图所示:
(2)如上图所示,
(3)解:如图所示,
【点睛】本题考查了直线、射线、线段,是基础题,主要是对语言文字转化为图形语言的能力的考查.
22.
【分析】根据,得出,根据得出,然后整体代入求出结果即可.
【详解】解:∵,
∴
,
∴C、D之间的距离为.
【点睛】本题主要考查了线段之间的关系,代数式求值,解题的关键是熟练掌握线段之间的关系,求出.
23.北偏西
【分析】先根据角的和差得到的度数,根据得到的度数,再根据角的和差得到的方向.
【详解】.解:∵射线的方向是北偏东,射线的方向是东偏北,
∴
∵平分,
∴,
∵,
∴,
所以射线方向是北偏西.
【点睛】本题考查了方位角,方位角是表示方向的角,以正北、正南方向为基准,来描述物体所处的方向.利用角的和差得出与正北方的夹角是解题关键.
24.(1)
(2)或
【分析】(1)根据题意可求出.再根据和平分,可求出,,进而可求出;
(2)分类讨论:当在内部时,设,则,由,可列出关于x的方程,解出x的值,即得出的大小,最后由计算即可;②当在外部时,设,则,由,可列出关于y的方程,解出y的值,即得出的大小,最后由计算即可.
【详解】(1)解:∵,,
∴.
∵,,
∴.
∵平分,
∴,
∴.
(2)分类讨论:①如图,当在内部时,
设,
∵,
∴,
∵,
∴,
解得:,
∴.
∵,
∴;
②如图,当在外部时,
设,则,
∵,
∴,
解得:,
∴.
∴.
故答案为:或.
【点睛】本题考查角平分线的有关计算,角的n等分点的有关计算,一元一次方程的应用.利用数形结合和分类讨论的思想是解题关键.
25.(1)
(2)
(3)
【分析】(1)求出,根据角平分线定义求出,即可求出答案;
(2)求出和,根据角平分线定义即可求出答案;
(3)求出和,根据角平分线定义即可求出答案.
【详解】(1)解:是直角,,
,
平分,
;
(2)理由如下:
是直角,,
,
,
平分
(3)如图,
是直角,,
,
,
,
平分,
故答案为:.
【点睛】本题主要考查的是角的计算,根据的位置进行分析是解题的关键.
26.平分,理由见解析
【分析】根据角平分线的定义以及等角的余角相等逐步推理证明,即可得到结论.
【详解】答:平分.
理由:因为是的平分线,所以.
因为,所以,
.
因为,
所以.
所以平分.
【点睛】此题考查角平分线的定义,等角的余角相等的性质,熟练掌握角平分线的定义,以及等角的余角相等是解题的关键.
27.(1)见解析
(2)点A在直线外
(3)两点之间线段最短
【分析】对于(1),根据直线,射线,线段的定义解答;
对于(2),根据点和直线的位置关系解答即可;
对于(3),根据线段的性质解答即可.
【详解】(1)如图,直线,射线,线段即为所求
(2)点在直线外(或直线不经过点);
故答案为:点在直线外(或直线不经过点);
(3)两点之间线段最短.
故答案为:两点之间线段最短.
【点睛】本题主要考查了线段,直线,射线,掌握和理解定义是解题的关键.
28.(1)见解析;
(2)见解析;
(3)①见解析;②6.
【分析】(1)根据直线的定义画出图形即可;
(2)根据射线的定义画出图形即可;
(3)①根据线段的定义以及题目要求画出图形即可;
②根据线段中点的定义求解即可.
【详解】(1)如图,直线即为所求;
(2)如图,射线即为所求;
(3)①如图,线段即为所求;
②∵,
∴,
故答案为:6.
【点睛】本题考查作图-复杂作图,直线,射线,线段的定义等知识,解题的关键是理解直线,射线,线段的定义,属于中考基础题.
29.(1)2
(2)2或10
(3)不变,画图见解析,
【分析】(1)根据数轴上的点向右移动用加法,向左移动用减法求出点P表示的数,再根据两点间的距离计算;
(2)设表示的数为,求出x值,再分两种情况计算;
(3)分在、之间,在点的左侧,在的右侧,三种情况,根据中点的定义计算即可.
【详解】(1)解:由图知:点表示的数为,
则表示的数为:,
,
、两点间的距离是2个单位长度;
(2)设表示的数为,
则,
解得:或,
当时,,
当时,,
∴m的值为2或10;
(3)点为的中点,点为的中点,
,,
当点在点、之间时,如图,
则
;
当点在点的左侧时,如图,
;
当点在点的右侧时,如图,
;
点在运动过程中,线段的长度不会发生变化,值为3.
【点睛】本题考查了数轴上两点之间的距离,中点的定义,利用数形结合思想和分类讨论思想是解题的关键.
30.(1)见解析
(2)
【分析】(1)根据题意画出图形即可;
(2)根据题意先求出的长度,然后将的长转化为的长度关系,求解即可.
【详解】(1)解:如图即为所作:
(2)如图,
∵,
∴,
∵为中点,
∴,
∴,
∵,
∴,即,
∵,
∴.
【点睛】本题考查了简单作图,关于中点的计算,线段之间的数量关系,理清题意,熟练运算中点的定义解题是本题的关键.
31.(1)9个
(2)
(3)平分,过程见解析
【分析】(1)根据角的定义进行求解即可;
(2)根据角平分线的定义得到,再根据平角的定义进行求解即可;
(3)先求出的度数,进而求出的度数,由此即可得到结论.
【详解】(1)解:由题意得,图中小于平角的角有,
∴图中有9个小于平角的角;
(2)解:∵平分,
∴,
∴;
(3)解:∵
∴,
∴,
∴平分.
【点睛】本题主要考查了几何图形中角度的计算,角平分线的定义,角的概念,灵活运用所学知识是解题的关键.
一、单选题
1.(2023上·山东临沂·七年级统考期末)如图,正方体的6个面上分别标有汉字“河”“东”“初”“中”“数”“学”,将该正方体按图示方式转动,根据图形可得与“学”相对的是( )
A.河 B.东 C.初 D.数
2.(2023上·山东济南·七年级统考期末)下列几何体中,从左面看得到的图是三角形的是( )
A. B.
C. D.
3.(2022上·山东威海·七年级统考期末)如图,将一张正方形纸片沿对角线折叠一次,得到一个三角形.在得到的三角形的三个内角各剪去一个圆,然后将纸片展开,得到的图案是( )
A. B.
C. D.
4.(2023上·山东滨州·七年级统考期末)由如图的正方体平面展开图可知,此正方体的“绿”字所在面的对面汉字是( )
A.低 B.碳 C.发 D.展
5.(2023上·山东济南·七年级统考期末)如图是一个正方体的表面展开图,这个正方体相对表面上所标的数字相等,则的值为( )
A. B.-1 C.0 D.4
6.(2023上·山东德州·七年级校考期末)如下图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和五边形,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图是( )
A. B. C. D.
7.(2023上·山东临沂·七年级统考期末)中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
8.(2023上·山东济南·七年级统考期末)卡塔尔世界杯已降下帷幕.为了筹办本届世界杯,卡塔尔耗资建造了座各具特色的球场.如图,阿图玛玛体育场位于多哈西南部,形状类似于圆柱体,外墙带有丰富的花边状装饰.下列图形绕虚线旋转一周,能形成圆柱体的是( )
A. B. C. D.
9.(2023上·山东菏泽·七年级统考期末)有下列生活、生产现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定同一行两棵树的位置,就能确定这行树所在的直线;④在正常条件下射击,要保证目标在准星和缺口确定的直线上,才能射中目标.其中能用“两点确定一条直线”来解释的现象有( )
A.①② B.①③ C.①④ D.①③④
10.(2023上·山东枣庄·七年级统考期末)在直线上取A,B,C三点,使得,如果O是线段的中点,那么线段的长为( )
A. B. C.或 D.以上结论都不对
11.(2023上·山东临沂·七年级统考期末)下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段的长度叫两点的距离;
③两点之间线段最短;
④如果,则点B是的中点;
⑤直线经过点A,那么点A在直线上.
A.2个 B.3个 C.4个 D.5个
12.(2023上·山东临沂·七年级统考期末)如图,学校在蕾蕾家南偏西的方向上,点表示超市所在的位置,,则超市在蕾蕾家的( )
A.北偏东的方向上 B.南偏东的方向上
C.北偏东的方向上 D.南偏东的方向上
13.(2023上·山东临沂·七年级统考期末)如图,将一个三角板角的顶点与另一个三角板的直角顶点重合,,则的度数是( )
A. B. C. D.
二、填空题
14.(2023上·山东济南·七年级统考期末)11月29日,神舟十五号载人飞船发射取得圆满成功.七年级学生设计了正方体礼盒庆祝,弘扬“载人航天精神”,如图,“神”字可加在下列 序号正方形中,使它们构成完整的正方体展开图(请写出所有可能的序号)
15.(2023上·山东济宁·七年级统考期末)小强有6个大小一样的正方形,他已用5个正方形拼成了如图所示的图形(阴影部分),要想使拼接的图形能够折叠成一个封闭的正方体盒子,他的第6个正方形可放在 的位置(填写序号).
16.(2023上·山东枣庄·七年级统考期末)若线段,点C是线段的中点,点D是线段的三等分点,则线段的长为 .
17.(2023上·山东枣庄·七年级统考期末)上午8点30分,钟面上时针与分针的夹角是 .
18.(2023上·山东临沂·七年级统考期末)比较大小: .(用“>”、“<”或“=”填空)
19.(2023上·山东济南·七年级统考期末)计算: .
20.(2023上·山东临沂·七年级统考期末)已知,则的余角是 .(填具体角度)
三、问答题
21.(2023上·山东菏泽·七年级统考期末)如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)在图①中,画线段交于E点;
(2)在图①中作射线;
(3)在图②中取一点P,使点P既在直线上又在直线上.
22.(2023上·山东济宁·七年级统考期末)A、B、C、D四个车站的位置如图所示,A、B两站之间的距离,B、C两站之间的距离,B、D两站之间的距离.若A、C两站之间的距离,求C、D两站之间的距离.
23.(2023上·山东滨州·七年级统考期末)如图所示,射线的方向是北偏东,射线的方向是东偏北,若平分,则射线的方向是北偏西多少度?
24.(2023上·山东滨州·七年级统考期末)已知,在内部作射线,使得.
(1)如图,在内部作射线,使得;作射线平分,求的度数;
(2)如果过点作射线,使得,则的度数为______.(不需写演推过程)
25.(2023上·山东临沂·七年级统考期末)已知是直线上的一点,是直角,平分.
(1)在图1中,若,求的度数;
(2)将图1中的绕顶点顺时针旋转至图2的位置,若,试用含的式子表示;
(3)继续旋转至图3的位置,若,其他条件不变,试将图形补充完整,则_____(用含的式子表示).
26.(2023上·山东济宁·七年级统考期末)如图,点,,在同一条直线上,平分,.平分吗?请说明理由.
四、作图题
27.(2023上·山东临沂·七年级统考期末)如图,、、是平面上三个点,按要求画出图形,并回答问题.
(1)作直线,射线,线段;
(2)请用适当的语句表述点与直线的关系:________;
(3)从点到点的所有线中,线段最短,其理论依据是________;
28.(2023上·山东济宁·七年级统考期末)如图,平面上不共线的三点A、B、C,请按如下要求作图:
(1)画直线;
(2)画射线;
(3)①延长线段AC至D,使;
②在①的条件下,若,则 .(直接写出答案)
29.(2023上·山东临沂·七年级统考期末)点A、B在数轴上所表示的数如图所示,P是数轴上一点:
(1)将点B在数轴上向左移动2个单位长度,再向右移动6个单位长度,得到点P,则A、P两点间的距离是______个单位长度.
(2)若点B在数轴上移动了m个单位长度到点P,且A、P两点间的距离是4,则______.
(3)若点M为的中点,点N为的中点,点P在运动过程中,线段的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段的长度.
30.(2023上·山东滨州·七年级统考期末)已知线段,延长到,使得,然后反向延长线段到,使得.
(1)请根据题意画出图形;
(2)若点为线段的中点,且,求的长.
五、计算题
31.(2022上·山东枣庄·七年级校考期末)如图,O为直线上一点,,平分.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出的度数;
(3)请通过计算说明是否平分.
参考答案:
1.C
【分析】根据题意,理解旋转过程中,各个面的变化情况.
【详解】由第一次旋转知,与“中”相对的是“数”,由第二次旋转知,与“学”相对是的“学”,
故选:C
【点睛】本题考查简单的几何体,具备一定的空间想象能力是解题的关键.
2.C
【分析】利用从左面看所得到的图形,进而分析得出即可.
【详解】解:A、从左面看得到的图是圆,不符合题意;
B、从左面看得到的图是圆,不符合题意;
C、从左面看得到的图三角形,符合题意;
D、从左面看得到的图等腰梯形,不符合题意;
故选:C.
【点睛】本题考查了从三个方向看物体的形状,掌握定义是关键.
3.A
【分析】由平面图形的折叠及立体图形的表面展开图的特点解结合实际操作解题.
【详解】解:在三角形的角上剪洞,展开后洞肯定还是在角上,排除C和D;
画出折叠线,两个三角形中每个三角形的角上都有一个洞,排除B;
所以答案为A;
故选:A.
【点睛】本题考查学生的空间想象能力和动手实践能力,熟练掌握空间想象能力是解题的关键.
4.C
【分析】根据正方体的表面展开图,相对的面之间一定相隔一个正方形,即可求解.
【详解】解:这是一个正方体的平面展开图,共有六个面,其中面“色”与面“碳”相对,面“绿”与面“发”相对,面“低”与面“展”相对.
故选:C
【点睛】本题主要考查了正方体的平面展开图的特征,熟练掌握正方体的表面展开图,相对的面之间一定相隔一个正方形是解题的关键.
5.A
【分析】根据题意可得先找出x和y的相对面,根据相对表面上所标的数字相等即可得到x和y的值,
【详解】解:由图可知:x的相对面是,y的相对面是,
∵相对表面上所标的数字相等,
∴,
∴,
故选:A.
【点睛】本题考查了正方体相对两个面上的文字,掌握找正方体相对两个面上的文字的方法,注意正方体的空间图形,从相对面入手,分析解答问题是解题的关键.
6.C
【分析】本题考查正方体的表面展开图及空间想象能力.在验证立方体的展开图时,要细心观察每一个标志的位置是否一致,然后进行判断.
【详解】解:把四个选项的展开图折叠,能复原的是C.
故选:C.
【点睛】本题考查了正方体的展开图,解决本题的关键是熟练掌握正方体的展开图,解决这类问题时,不妨动手实际操作一下,即可解决问题.
7.A
【分析】枪挑是用枪尖挑,枪尖可看作点,棍可看作线,转化成数学思想即可.
【详解】所以由题意可得:从数学的角度可解释为点动成线,线动成面.
故选:A.
【点睛】本题考查了点、线、面、体的知识点,熟练掌握点、线、面之间的关系是解题的关键.
8.C
【分析】根据选项中图形的特点,圆柱体的特点,进行对比即可求解.
【详解】解:.旋转后是圆台,不符题意;
.旋转后是球,不符题意;
.旋转后是圆柱体,符合题意;
.旋转后是圆锥,不符题意;
故选:.
【点睛】本题主要考查立体几何的平面图,结合立体图形的特点,平面图形的特点是解题的关键.
9.D
【分析】根据两点确定一条直线,两点之间线段最短的性质逐一对各选项进行判断即可得到答案.
【详解】解:①利用了两点确定一条直线的性质,符合题意;
②利用了两点之间线段最短的性质,不符合题意;
③利用了两点确定一条直线的性质,符合题意;
④利用了两点确定一条直线的性质,符合题意,
能用“两点确定一条直线”来解释的现象有①③④,
故选D.
【点睛】本题考查了线段的性质以及直线的性质,正确理解并熟记相关性质公理是解题关键,属于基础题.
10.C
【分析】分两种情况,即B在之间,C在之间,先求出的长度,再根据线段中点的定义求出的长度即可.
【详解】①如图,
∵,
∴,
∵O是线段的中点,
∴
②如图,
∵,
∴,
∵O是线段的中点,
∴
故选C.
【点睛】此题主要考查线段中点的定义和线段的和差,熟练掌握线段中点定义是解题关键.
11.C
【分析】根据点和直线的位置关系,直线的性质,线段的性质,两点之间的距离的定义逐个判断即可.
【详解】解:过两点有且只有一条直线,故①正确;
连接两点的线段的长度叫两点的距离,故②正确;
两点之间,线段最短,故③正确;
当在直线外时,,则点不是的中点,故④错误;
直线经过点,那么点在直线上,故⑤正确,
即正确的有4个,
故选:C.
【点睛】本题考查了点和直线的位置关系,直线的性质,线段的性质,两点之间的距离的定义的应用,能熟记知识点是解此题的关键.
12.D
【分析】直接利用方向角的定义得出的度数.
【详解】如图所示:
由题意可得: , ,
则 ,
故超市在蕾蕾家的南偏东 的方向上.
故选:D.
【点睛】本题考查了方向角的定义,解题的关键是正确根据图形得出的度数.
13.A
【分析】利用求出的度数,再用求出的度数.
【详解】解:由图可知:,
;
故选:A.
【点睛】本题考查三角板中角的计算.根据图形,理清角的和差关系,是解题的关键.
14.①②③
【分析】根据正方体表面展开图的特征即可得出答案.
【详解】解:“神”字可加在①②③的位置,
故答案为:①②③.
【点睛】本题考查正方体的展开图特点,掌握正方体表面展开图的特征是正确解题的关键.
15.③
【分析】根据正方体的表面展开图分析即可求解.
【详解】解:如图所示,
故答案为:③.
【点睛】本题考查了正方体的表面展开图,理正方体的表面展开图的模型是解题的关键.正方体的表面展开图用‘口诀’:一线不过四,田凹应弃之,相间、Z端是对面,间二、拐角邻面知.
16.或
【分析】根据线段中点的定义和线段三等分点的定义即可得到结论.
【详解】解:是线段的中点,,
,
点是线段的三等分点,
①当时,如图,
;
②当时,如图,
.
所以线段的长为或.
故答案为:或.
【点睛】本题考查了两点间的距离,线段中点的定义,分类讨论思想的运用是解题的关键.
17./度
【分析】根据分针每分钟转,时针每分钟转,结合钟面被分成12大格,每大格可计算出30分钟时针与分针所转的角度,所以此时钟面上时针与分针夹角的度数.
【详解】解:30分钟,钟面上时针从8开始转的度数为,
所以此时钟面上时针与分针夹角的度数.
故答案为:.
【点睛】本题考查了钟面角:掌握“钟面被分成12大格,每大格;分针每分钟转,时针每分钟转”是解本题的关键.
18.
【分析】先根据度分秒的换算,把和全化成秒,再比较大小即可.
【详解】解:∵
,
∴.
故答案为:.
【点睛】此题考查了度分秒的换算,关键是把和化成秒,转化时要注意单位统一.
19.
【分析】根据计算即可得出答案.
【详解】
故答案为:
【点睛】本题主要考查角的运算,熟记,是解题的关键.
20.
【分析】直接根据余角的定义即可求解.
【详解】解:∵,
∴的余角=,
故答案为:.
【点睛】本题考查了余角的定义,解题关键是掌握互余的两个角相加为.
21.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据线段的定义画图即可;
(2)以B为端点画射线即可;
(3)作直线和直线相交,交点即为点P.
【详解】(1)如图所示:
(2)如上图所示,
(3)解:如图所示,
【点睛】本题考查了直线、射线、线段,是基础题,主要是对语言文字转化为图形语言的能力的考查.
22.
【分析】根据,得出,根据得出,然后整体代入求出结果即可.
【详解】解:∵,
∴
,
∴C、D之间的距离为.
【点睛】本题主要考查了线段之间的关系,代数式求值,解题的关键是熟练掌握线段之间的关系,求出.
23.北偏西
【分析】先根据角的和差得到的度数,根据得到的度数,再根据角的和差得到的方向.
【详解】.解:∵射线的方向是北偏东,射线的方向是东偏北,
∴
∵平分,
∴,
∵,
∴,
所以射线方向是北偏西.
【点睛】本题考查了方位角,方位角是表示方向的角,以正北、正南方向为基准,来描述物体所处的方向.利用角的和差得出与正北方的夹角是解题关键.
24.(1)
(2)或
【分析】(1)根据题意可求出.再根据和平分,可求出,,进而可求出;
(2)分类讨论:当在内部时,设,则,由,可列出关于x的方程,解出x的值,即得出的大小,最后由计算即可;②当在外部时,设,则,由,可列出关于y的方程,解出y的值,即得出的大小,最后由计算即可.
【详解】(1)解:∵,,
∴.
∵,,
∴.
∵平分,
∴,
∴.
(2)分类讨论:①如图,当在内部时,
设,
∵,
∴,
∵,
∴,
解得:,
∴.
∵,
∴;
②如图,当在外部时,
设,则,
∵,
∴,
解得:,
∴.
∴.
故答案为:或.
【点睛】本题考查角平分线的有关计算,角的n等分点的有关计算,一元一次方程的应用.利用数形结合和分类讨论的思想是解题关键.
25.(1)
(2)
(3)
【分析】(1)求出,根据角平分线定义求出,即可求出答案;
(2)求出和,根据角平分线定义即可求出答案;
(3)求出和,根据角平分线定义即可求出答案.
【详解】(1)解:是直角,,
,
平分,
;
(2)理由如下:
是直角,,
,
,
平分
(3)如图,
是直角,,
,
,
,
平分,
故答案为:.
【点睛】本题主要考查的是角的计算,根据的位置进行分析是解题的关键.
26.平分,理由见解析
【分析】根据角平分线的定义以及等角的余角相等逐步推理证明,即可得到结论.
【详解】答:平分.
理由:因为是的平分线,所以.
因为,所以,
.
因为,
所以.
所以平分.
【点睛】此题考查角平分线的定义,等角的余角相等的性质,熟练掌握角平分线的定义,以及等角的余角相等是解题的关键.
27.(1)见解析
(2)点A在直线外
(3)两点之间线段最短
【分析】对于(1),根据直线,射线,线段的定义解答;
对于(2),根据点和直线的位置关系解答即可;
对于(3),根据线段的性质解答即可.
【详解】(1)如图,直线,射线,线段即为所求
(2)点在直线外(或直线不经过点);
故答案为:点在直线外(或直线不经过点);
(3)两点之间线段最短.
故答案为:两点之间线段最短.
【点睛】本题主要考查了线段,直线,射线,掌握和理解定义是解题的关键.
28.(1)见解析;
(2)见解析;
(3)①见解析;②6.
【分析】(1)根据直线的定义画出图形即可;
(2)根据射线的定义画出图形即可;
(3)①根据线段的定义以及题目要求画出图形即可;
②根据线段中点的定义求解即可.
【详解】(1)如图,直线即为所求;
(2)如图,射线即为所求;
(3)①如图,线段即为所求;
②∵,
∴,
故答案为:6.
【点睛】本题考查作图-复杂作图,直线,射线,线段的定义等知识,解题的关键是理解直线,射线,线段的定义,属于中考基础题.
29.(1)2
(2)2或10
(3)不变,画图见解析,
【分析】(1)根据数轴上的点向右移动用加法,向左移动用减法求出点P表示的数,再根据两点间的距离计算;
(2)设表示的数为,求出x值,再分两种情况计算;
(3)分在、之间,在点的左侧,在的右侧,三种情况,根据中点的定义计算即可.
【详解】(1)解:由图知:点表示的数为,
则表示的数为:,
,
、两点间的距离是2个单位长度;
(2)设表示的数为,
则,
解得:或,
当时,,
当时,,
∴m的值为2或10;
(3)点为的中点,点为的中点,
,,
当点在点、之间时,如图,
则
;
当点在点的左侧时,如图,
;
当点在点的右侧时,如图,
;
点在运动过程中,线段的长度不会发生变化,值为3.
【点睛】本题考查了数轴上两点之间的距离,中点的定义,利用数形结合思想和分类讨论思想是解题的关键.
30.(1)见解析
(2)
【分析】(1)根据题意画出图形即可;
(2)根据题意先求出的长度,然后将的长转化为的长度关系,求解即可.
【详解】(1)解:如图即为所作:
(2)如图,
∵,
∴,
∵为中点,
∴,
∴,
∵,
∴,即,
∵,
∴.
【点睛】本题考查了简单作图,关于中点的计算,线段之间的数量关系,理清题意,熟练运算中点的定义解题是本题的关键.
31.(1)9个
(2)
(3)平分,过程见解析
【分析】(1)根据角的定义进行求解即可;
(2)根据角平分线的定义得到,再根据平角的定义进行求解即可;
(3)先求出的度数,进而求出的度数,由此即可得到结论.
【详解】(1)解:由题意得,图中小于平角的角有,
∴图中有9个小于平角的角;
(2)解:∵平分,
∴,
∴;
(3)解:∵
∴,
∴,
∴平分.
【点睛】本题主要考查了几何图形中角度的计算,角平分线的定义,角的概念,灵活运用所学知识是解题的关键.
