沪教版五年级下册数学4、表面积的变化 课件(17张ppt)
文档属性
| 名称 | 沪教版五年级下册数学4、表面积的变化 课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 256.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
表面积的变化 ②
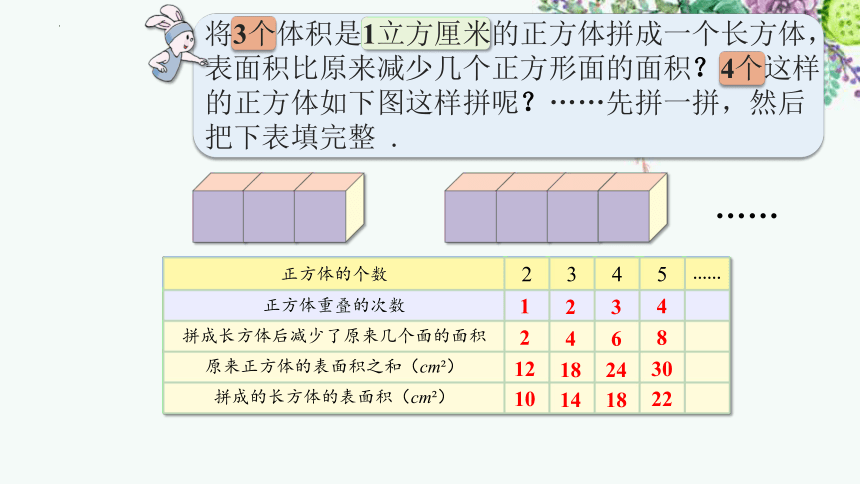
将3个体积是1立方厘米的正方体拼成一个长方体,表面积比原来减少几个正方形面的面积?4个这样的正方体如下图这样拼呢?……先拼一拼,然后把下表填完整 .
正方体的个数 2 3 4 5 ……
正方体重叠的次数
拼成长方体后减少了原来几个面的面积
原来正方体的表面积之和(cm )
拼成的长方体的表面积(cm )
1
12
10
2
2
18
14
4
3
24
18
6
4
30
22
8
……
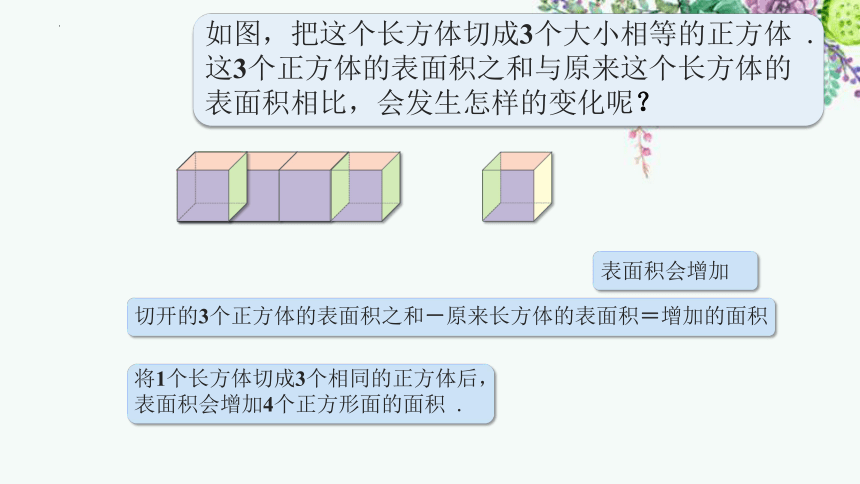
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
表面积会增加
切开的3个正方体的表面积之和-原来长方体的表面积=增加的面积
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
将1个长方体切成3个相同的正方体后,表面积会增加4个正方形面的面积 .
表面积会增加
切开的3个正方体的表面积之和-原来长方体的表面积=增加的面积
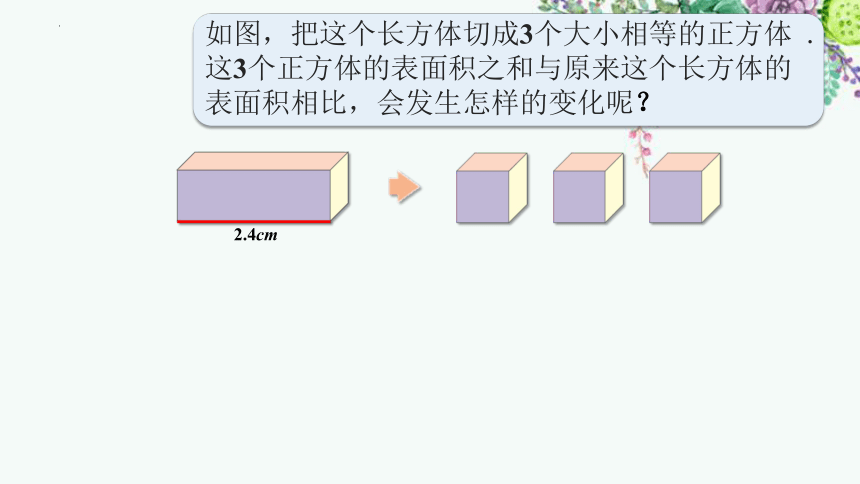
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
2.4cm
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
6× ( 0.8×0.8 )
=6×0.64
=3.84 (cm )
2.4÷3=0.8 (cm)
3×3.84=11.52(cm )
0.8×2.4×4+0.8×0.8×2
=7.68+1.28
=8.96(cm )
11.52-8.96=2.56(cm )
2.4cm
0.8cm
0.8cm
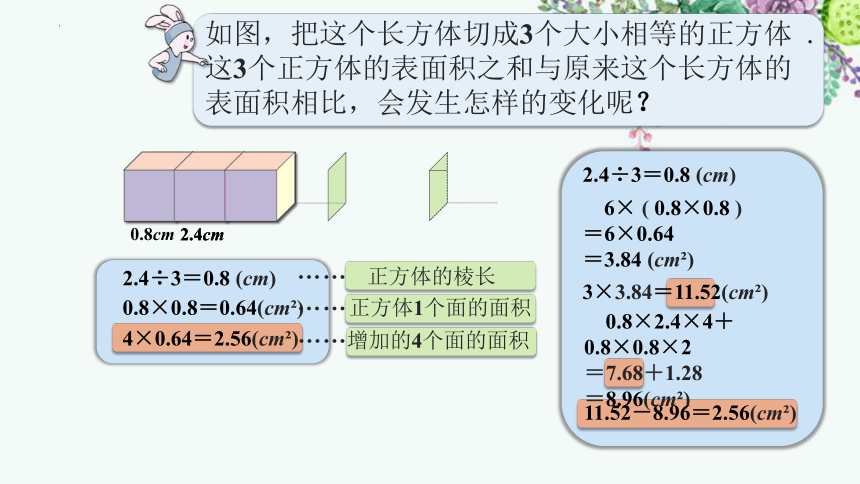
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
2.4÷3=0.8 (cm)
0.8×0.8=0.64(cm )
4×0.64=2.56(cm )
6× ( 0.8×0.8 )
=6×0.64
=3.84 (cm )
2.4÷3=0.8 (cm)
3×3.84=11.52(cm )
0.8×2.4×4+0.8×0.8×2
=7.68+1.28
=8.96(cm )
11.52-8.96=2.56(cm )
2.4cm
0.8cm
0.8cm
0.8cm
2.4cm
正方体的棱长
……
正方体1个面的面积
……
增加的4个面的面积
……
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
2.4÷3=0.8 (cm)
0.8×0.8=0.64(cm )
4×0.64=2.56(cm )
重叠的次数×2=减少的面的个数
切开的次数×2=增加的面的个数
2.4cm
6× ( 0.8×0.8 )
=6×0.64
=3.84 (cm )
2.4÷3=0.8 (cm)
3×3.84=11.52(cm )
0.8×2.4×4+0.8×0.8×2
=7.68+1.28
=8.96(cm )
11.52-8.96=2.56(cm )
正方体的棱长
……
正方体1个面的面积
……
增加的4个面的面积
……
86÷4=21.5 (cm )
516÷6=86 (cm )
6×21.5=129 (cm )
8×129=1032 (cm )
1032-516=516 (cm )
如图,把一个表面积是516平方厘米的正方体切割成8个相等的小正方体(无剩余,损耗不计),切割后的8个小正方体的表面积之和比原来大正方体的表面积增加多少平方厘米?
大正方体每个面的面积
……
小正方体每个面的面积
……
1个小正方体的表面积
……
8个小正方体的表面积
……
增加面的面积
……
增加大正方形面的个数:3×2=6 (个)
增加的表面积:
大正方体每个面的面积:516÷6=86 (cm )
516
×86= (cm )
258
3
6
如图,把一个表面积是516平方厘米的正方体切割成8个相等的小正方体(无剩余,损耗不计),切割后的8个小正方体的表面积之和比原来大正方体的表面积增加多少平方厘米?
表面积增加516平厘米 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
小挑战
体积减少 .
顶点处:表面积没有发生变化 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
小挑战
顶点处:表面积没有发生变化 .
小挑战
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
顶点处:表面积没有发生变化 .
小挑战
棱中间:增加2个小正方形的面积 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
顶点处:表面积没有发生变化 .
小挑战
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
棱中间:增加2个小正方形的面积 .
顶点处:表面积没有发生变化 .
小挑战
面中间:增加4个小正方形的面积 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
棱中间:增加2个小正方形的面积 .
顶点处:表面积没有发生变化 .
小挑战
面中间:增加4个小正方形的面积 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
棱中间:增加2个小正方形的面积 .
顶点处:表面积没有发生变化 .
表面积的变化 ②
将3个体积是1立方厘米的正方体拼成一个长方体,表面积比原来减少几个正方形面的面积?4个这样的正方体如下图这样拼呢?……先拼一拼,然后把下表填完整 .
正方体的个数 2 3 4 5 ……
正方体重叠的次数
拼成长方体后减少了原来几个面的面积
原来正方体的表面积之和(cm )
拼成的长方体的表面积(cm )
1
12
10
2
2
18
14
4
3
24
18
6
4
30
22
8
……
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
表面积会增加
切开的3个正方体的表面积之和-原来长方体的表面积=增加的面积
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
将1个长方体切成3个相同的正方体后,表面积会增加4个正方形面的面积 .
表面积会增加
切开的3个正方体的表面积之和-原来长方体的表面积=增加的面积
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
2.4cm
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
6× ( 0.8×0.8 )
=6×0.64
=3.84 (cm )
2.4÷3=0.8 (cm)
3×3.84=11.52(cm )
0.8×2.4×4+0.8×0.8×2
=7.68+1.28
=8.96(cm )
11.52-8.96=2.56(cm )
2.4cm
0.8cm
0.8cm
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
2.4÷3=0.8 (cm)
0.8×0.8=0.64(cm )
4×0.64=2.56(cm )
6× ( 0.8×0.8 )
=6×0.64
=3.84 (cm )
2.4÷3=0.8 (cm)
3×3.84=11.52(cm )
0.8×2.4×4+0.8×0.8×2
=7.68+1.28
=8.96(cm )
11.52-8.96=2.56(cm )
2.4cm
0.8cm
0.8cm
0.8cm
2.4cm
正方体的棱长
……
正方体1个面的面积
……
增加的4个面的面积
……
如图,把这个长方体切成3个大小相等的正方体 .这3个正方体的表面积之和与原来这个长方体的表面积相比,会发生怎样的变化呢?
2.4÷3=0.8 (cm)
0.8×0.8=0.64(cm )
4×0.64=2.56(cm )
重叠的次数×2=减少的面的个数
切开的次数×2=增加的面的个数
2.4cm
6× ( 0.8×0.8 )
=6×0.64
=3.84 (cm )
2.4÷3=0.8 (cm)
3×3.84=11.52(cm )
0.8×2.4×4+0.8×0.8×2
=7.68+1.28
=8.96(cm )
11.52-8.96=2.56(cm )
正方体的棱长
……
正方体1个面的面积
……
增加的4个面的面积
……
86÷4=21.5 (cm )
516÷6=86 (cm )
6×21.5=129 (cm )
8×129=1032 (cm )
1032-516=516 (cm )
如图,把一个表面积是516平方厘米的正方体切割成8个相等的小正方体(无剩余,损耗不计),切割后的8个小正方体的表面积之和比原来大正方体的表面积增加多少平方厘米?
大正方体每个面的面积
……
小正方体每个面的面积
……
1个小正方体的表面积
……
8个小正方体的表面积
……
增加面的面积
……
增加大正方形面的个数:3×2=6 (个)
增加的表面积:
大正方体每个面的面积:516÷6=86 (cm )
516
×86= (cm )
258
3
6
如图,把一个表面积是516平方厘米的正方体切割成8个相等的小正方体(无剩余,损耗不计),切割后的8个小正方体的表面积之和比原来大正方体的表面积增加多少平方厘米?
表面积增加516平厘米 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
小挑战
体积减少 .
顶点处:表面积没有发生变化 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
小挑战
顶点处:表面积没有发生变化 .
小挑战
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
顶点处:表面积没有发生变化 .
小挑战
棱中间:增加2个小正方形的面积 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
顶点处:表面积没有发生变化 .
小挑战
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
棱中间:增加2个小正方形的面积 .
顶点处:表面积没有发生变化 .
小挑战
面中间:增加4个小正方形的面积 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
棱中间:增加2个小正方形的面积 .
顶点处:表面积没有发生变化 .
小挑战
面中间:增加4个小正方形的面积 .
如图,把一个大正方体切割成若干个大小相等的小正方体(无剩余,损耗不计),在这个大正方体上拿走一个小正方体后,剩下部分的表面积与原大正方体的表面积相比,会发生变化吗?
棱中间:增加2个小正方形的面积 .
顶点处:表面积没有发生变化 .
