勾股定理复习课件2 (勾股定理的应用思想)
文档属性
| 名称 | 勾股定理复习课件2 (勾股定理的应用思想) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-10 13:51:34 | ||
图片预览



文档简介
课件17张PPT。勾股定理的应用思想綦江区古南中学 沈志惠 基础练习
1、分别以直角三角形三边为边作正方形,
则这三个正方形的面积A,B,C之间的关系
是_____
2、已知a、b、c是△ABC的三边长,且满足关系式 ,则△ABC的形状是_____
3、如图,两个正方形的面积分别为64,49,则AC=___ .
4、判断:以下列各组数据中a、b、c为边的三角形,是否是直角三角形,是则指出斜边
(1)a=3,b=4,c=5
(2)a=13,b=12,c=5
(3)a=2,b=4,c=3
(4)a=17,b=8,c=15
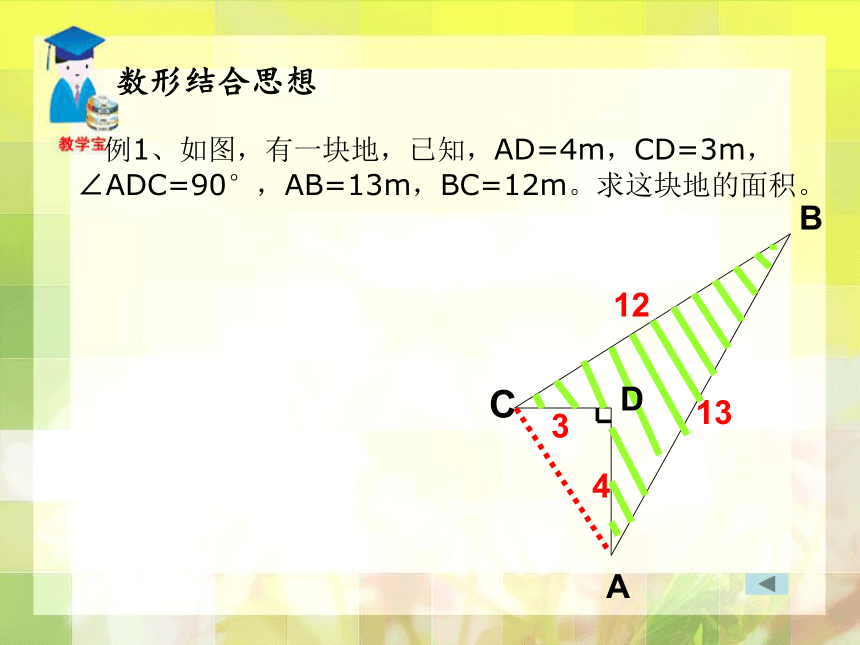
5、已知直角三角形的两边长是3、4,第三边长是________按直角三角形的直角边、斜边分类 例1、如图,有一块地,已知,AD=4m,CD=3m, ∠ADC=90°,AB=13m,BC=12m。求这块地的面积。数形结合思想
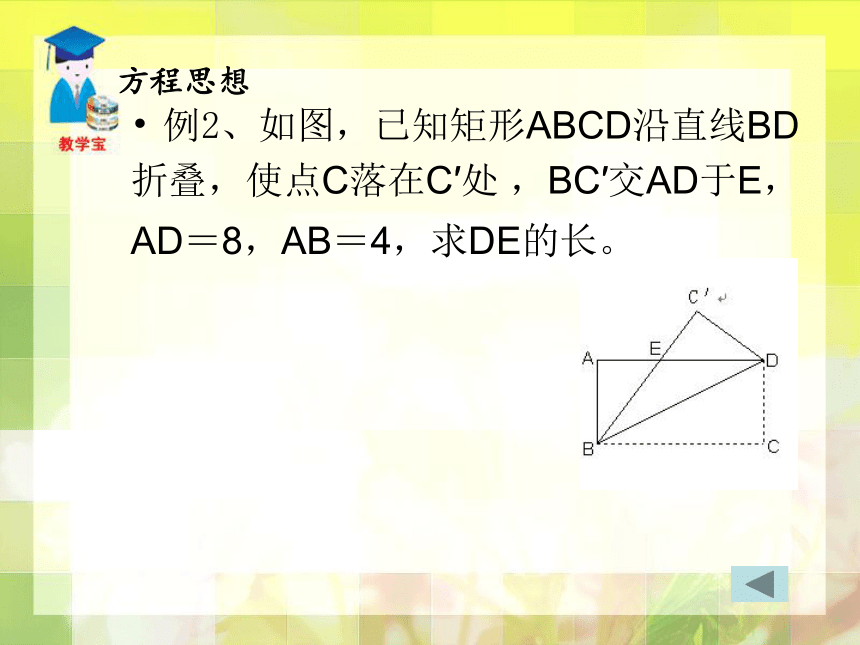
例2、如图,已知矩形ABCD沿直线BD
折叠,使点C落在C′处 ,BC′交AD于E,
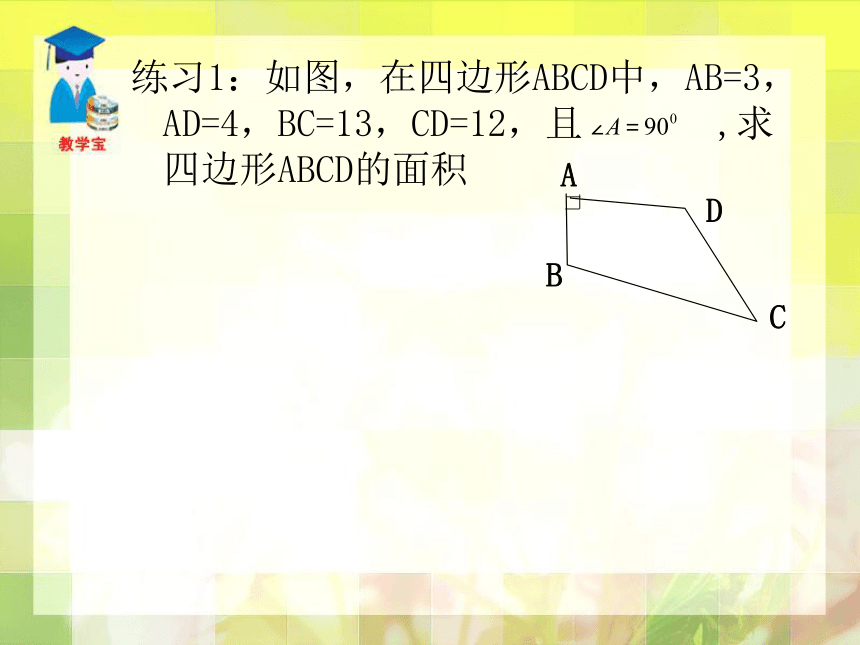
AD=8,AB=4,求DE的长。 方程思想练习1:如图,在四边形ABCD中,AB=3,AD=4,BC=13,CD=12,且 ,求四边形ABCD的面积练习2、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
方程思想D400100060°30°练习3、在△ABC中AB=15,AC=20,AD是BC边上的高,且AD=12,求BC的长
按高的位置分类 小结:通过练习与例题,你学到了什么1、勾股定理的数形结合2、利用勾股定理列方程3、审题要细心,注意分类讨论如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
课堂小结分析:判断三角形的形状要看三角形两边的平方和是否等于第三边的平方。
1、分别以直角三角形三边为边作正方形,
则这三个正方形的面积A,B,C之间的关系
是_____
2、已知a、b、c是△ABC的三边长,且满足关系式 ,则△ABC的形状是_____
3、如图,两个正方形的面积分别为64,49,则AC=___ .
4、判断:以下列各组数据中a、b、c为边的三角形,是否是直角三角形,是则指出斜边
(1)a=3,b=4,c=5
(2)a=13,b=12,c=5
(3)a=2,b=4,c=3
(4)a=17,b=8,c=15
5、已知直角三角形的两边长是3、4,第三边长是________按直角三角形的直角边、斜边分类 例1、如图,有一块地,已知,AD=4m,CD=3m, ∠ADC=90°,AB=13m,BC=12m。求这块地的面积。数形结合思想
例2、如图,已知矩形ABCD沿直线BD
折叠,使点C落在C′处 ,BC′交AD于E,
AD=8,AB=4,求DE的长。 方程思想练习1:如图,在四边形ABCD中,AB=3,AD=4,BC=13,CD=12,且 ,求四边形ABCD的面积练习2、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
方程思想D400100060°30°练习3、在△ABC中AB=15,AC=20,AD是BC边上的高,且AD=12,求BC的长
按高的位置分类 小结:通过练习与例题,你学到了什么1、勾股定理的数形结合2、利用勾股定理列方程3、审题要细心,注意分类讨论如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
课堂小结分析:判断三角形的形状要看三角形两边的平方和是否等于第三边的平方。
