中考数学 应用题怎样解
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
冲刺 中考数学 应用题怎样解
题型1?方程(组)型应用题
方程是描述丰富多彩的现实世界数量关系的最重要的语言,也是中考命题所要考察的重点热点之一。我们必须广泛了解现代社会中日常生活、生产实践、经济活动的有关常识。并学会用数学中方程的思想去分析和解决一些实际问题。解此类问题的方法是:(1)审题,明确未知量和已知量;(2)设未知数,务必写明意义和单位;(3)依题意,找出等量关系,列出等量方程;(4)解方程,必要时验根。
题型2?不等式(组)型应用题
现实世界中不等关系是普遍存在的,许多现实问题很难确定(有时也不需要确定)具体的数值。但可以求出或确定这一问题中某个量的变化范围(趋势),从而对所有研究问题的面貌有一个比较清楚的认识。本节中,我们所要讨论的问题大多是要求出某个量的取值范围或极端可能性,它们涉及我们日常生活中的方方面面。
列不等式时要从题意出发,设好未知量之后,用心体会题目所规定的实际情境,从中找出不等关系。
题型3?函数型应用问题
函数及其图象是初中数学中的主要内容之一,也是初中数学与高中数学相联系的纽带。它与代数、几何、三角函数等知识有着密切联系,中考命题中既重点考查函数及其图象的有关基础知识,同时以函数为背景的应用性问题也是命题热点之一,多数省市作压轴题。因此,在中考复习中,关注这一热点显得十分重要。解这类题的方法是对问题的审读和理解,掌握用一个变量的代数式表示另一个变量,建立两个变量间的等量关系,同时从题中确定自变量的取值范围。
题型4?统计型应用问题
统计的内容有着非常丰富的实际背景,其实际应用性特别强。中考试题的热点之一,就是考查统计思想方法,同时考查学生应用数学的意识和处理数据解决实际问题的能力。
题型5?几何型应用问题
几何应用题常常以现实生活情景为背景,考查学生识别图形的能力、动手操作图形的能力、运用几何知识解决实际问题的能力以及探索、发现问题的能力和观察、想像、分析、综合、比较、演绎、归纳、抽象、概括、类比、分类讨论、数形结合等数学思想方法。
例1.(2007天津市)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程。如果你选用其他的解题方案,此时,不必填写表格,只需按照解答题的一般要求,进行解答即可。
甲乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时。问二人每小时各走几千米?
(1)设乙每小时走x千米,根据题意,利用速度、时间、路程之间的关系填写下表。
(要求:填上适当的代数式,完成表格)
(2)列出方程(组),并求出问题的解。
解:(1)
(2)根据题意,列方程得
整理得
解这个方程得
经检验,都是原方程的根。但速度为负数不合题意
所以只取,此时
答:甲每小时走6千米,乙每小时走5千米。
例2.(2007乌兰察布盟)某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元。
(1) 求A、B两种品牌的化妆品每套进价分别为多少元?
(2) 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
解:(1)设A种品牌的化妆品每套进价为x元,B种品牌的化妆品每套进价为y元,得
解得
答:A、B两种品牌得化妆品每套进价分别为100元,75元。
(2)设A种品牌得化妆品购进m套,则B种品牌得化妆品购进(2m+4)套。
根据题意得:解得
∵m为正整数,∴m=16、17、18 ∴2m+4=36、38、40
答:有三种进货方案
(1) A种品牌得化妆品购进16套,B种品牌得化妆品购进36套。
(2) A种品牌得化妆品购进17套,B种品牌得化妆品购进38套。
A种品牌得化妆品购进18套,B种品牌得化妆品购进40套。
例3.(2007扬州)连接上海市区到浦东国际机场的磁悬浮轨道全长约为,列车走完全程包含启动加速、匀速运行、制动减速三个阶段.已知磁悬浮列车从启动加速到稳定匀速动行共需秒,在这段时间内记录下下列数据:
时间(秒) 0 50 100 150 200
速度(米/秒) 0 30 60 90 120
路程(米) 0 750 3000 6750 12000
(1)请你在一次函数、二次函数和反比例函数中选择合适的函数来分别表示在加速阶段()速度与时间的函数关系、路程与时间的函数关系.
(2)最新研究表明,此种列车的稳定动行速度可达180米/秒,为了检测稳定运行时各项指标,在列车达到这一速度后至少要运行100秒,才能收集全相关数据.若在加速过程中路程、速度随时间的变化关系仍然满足(1)中的函数关系式,并且制作减速所需路程与启动加速的路程相同.根据以上要求,至少还要再建多长轨道就能满足试验检测要求?
(3)若减速过程与加速过程完全相反.根据对问题(2)的研究,直接写出列车在试验检测过程中从启动到停车这段时间内,列车离开起点的距离(米)与时间(秒)的函数关系式(不需要写出过程)
解:(1)通过描点或找规律,确定与是一次函数,
与是二次函数,.
(2)由得当时,秒,则米千米.
米千米
因为减速所需路程和启动加速路程相同,所以总路程为
所以还需建千米.
(3)当时,
当时,
当时,(一般式为).
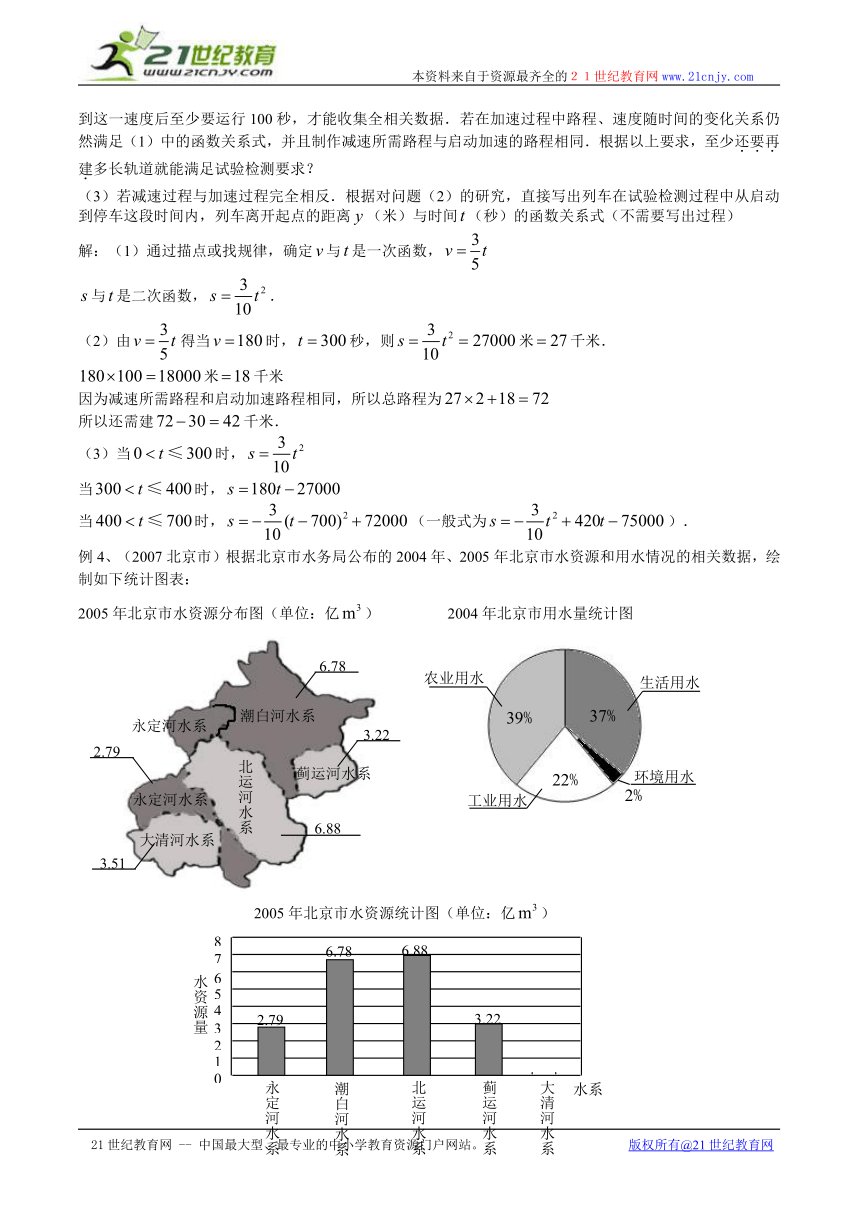
例4、(2007北京市)根据北京市水务局公布的2004年、2005年北京市水资源和用水情况的相关数据,绘制如下统计图表:
2005年北京市水资源分布图(单位:亿) 2004年北京市用水量统计图
2005年北京市用水情况统计表
生活用水 环境用水 工业用水 农业用水
用水量(单位:亿) 13.38 6.80 13.22
占全年总用水量的比例
(1)北京市水资源全部由永定河水系、潮白河水系、北运河水系、蓟运河水系、大清河水系提供.请你根据以上信息补全2005年北京市水资源统计图,并计算2005年全市的水资源总量(单位:亿);
(2)在2005年北京市用水情况统计表中,若工业用水量比环境用水量的6倍多0.2亿,请你先计算环境用水量(单位:亿),再计算2005年北京市用水总量(单位:亿);
(3)根据以上数据,请你计算2005年北京市的缺水量(单位:亿);
(4)结合2004年及2005年北京市的用水情况,谈谈你的看法.
解:(1)初全2005年北京市水资源统计图见右图;
水资源总量为亿.
(2)设2005年环境用水量为亿.
依题意得.
解得.
所以2005年环境用水量为亿.
因为,
所以2005年北京市用水总量为亿.
(3)因为,所以2005年北京市缺水量为亿.
(4)说明:通过对比2004年及2005年北京市的用水情况,能提出积极看法的给分.
例5、(2007荆门市)一、问题背景
某校九年级(1)班课题学习小组对家庭煤气的使用量做了研究,其实验过程和对数据的处理如下.
仔细观察现在家庭使用的电子打火煤气灶,发现当关着煤气的时候,煤气旋钮(以下简称旋钮)的位置为竖起方向,把这个位置定为0°,煤气开到最大时,位置为90°.(以0°位置作起始边,旋钮和起始边的夹角).在0~90°之间平均分成五等分,代表不同的煤气流量,它们分别是18°,36°,54°,72°,90°,见图1.
位置 烧开一壶水所需 流量
时间(分) 煤气量(m3) m3/分
18° 19 0.13 0.0068
36° 16 0.12 0.0076
54° 13 0.14 0.0107
72° 12 0.15 0.0124
90° 10 0.17 0.0172
在这些位置上分别以烧开一壶水(3.75升)为标准,记录所需的时间和所用的煤气量.并根据旋钮位置以及烧开一壶水所需时间(用t表示)、所用煤气量(用v表示),计算出不同旋钮位置所代表的煤气流量(用L表示),L=v/t,数据见右表.这样为可以研究煤气流量和烧开一壶水所需时间及用气量之间的关系了.
二、任务要求
1.作图:将下面图2中的直方图补充完整;在图3中作出流量与时间的折线图.
2.填空:①从图2可以看出,烧开一壶水所耗用的最少煤气量为_______m2,此时旋钮位置在______.
②从图3可以看出,不考虑煤气用量,烧开一壶水所用的最短时间为_______分钟,此时旋钮位置在______.
3.通过实验,请你对上述结果(用煤气烧水最省时和最省气)作一个简要的说明.
解:(1)(每图2分)…………………………………………………………………………4分
(2)0.12,36°;10,90°;(每空一分)………………………………………………………8分
(3)当旋钮开到36°附近时最省气,当旋钮开到90°时最省时.最省时和最省气不可能同时做到.………………………………………………………………………………………10分
说明:第(3)问只要表达意思明确即可,方式和文字不一定如此表达.
注:最省气的旋钮位置在36°附近,接近0°~90°的黄金分割点0.382(=0.4).
例6、(2007资阳)一座建于若干年前的水库大坝的横断面如图7所示,其中背水面的整个坡面是长为90米、宽为5米的矩形. 现需将其整修并进行美化,方案如下:① 将背水坡AB的坡度由1∶0.75改为1∶;② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花 .
⑴ 求整修后背水坡面的面积;
⑵ 如果栽花的成本是每平方米25元,种草的成本是每平方米20元,那么种植花草至少需要多少元?
解:⑴ 作AE⊥BC于E.
∵ 原来的坡度是1∶0.75,∴ = .
设AE=4k,BE=3k,∴ AB=5k,又 ∵ AB=5米,∴k=1,则AE=4米 .
设整修后的斜坡为,由整修后坡度为1∶,有
,∴∠=30°,
∴ 8米 . ∴ 整修后背水坡面面积为90×8=720米2 .
⑵ 将整修后的背水坡面分为9块相同的矩形,则每一区域的面积为80米2 .
解法一:∵ 要依次相间地种植花草,有两种方案:
第一种是种草5块,种花4块,需要20×5×80+25×4×80=16000元;
第二种是种花5块,种草4块,需要20×4×80+25×5×80=16400元 .
∴ 应选择种草5块、种花4块的方案,需要花费16000元 .
解法二:∵ 要依次相间地种植花草,则必然有一种是5块,有一种是4块,而栽花的成本是每平方米25元,种草的成本是每平方米20元,
∴ 两种方案中,选择种草5块、种花4块的方案花费较少 .
即:需要花费20×5×80+25×4×80=16000元 .
6.78
3.22
6.88
2.79
3.51
潮白河水系
永定河水系
蓟运河水系
北运河水系
永定河水系
大清河水系
农业用水
生活用水
工业用水
环境用水
0
1
2
3
4
5
6
7
8
水系
2.79
6.78
6.88
3.22
永定河水系
潮白河水系
北运河水系
蓟运河水系
大清河水系
水资源量
2005年北京市水资源统计图(单位:亿)
0
1
2
3
4
5
6
7
8
水系
2.79
6.78
6.88
3.22
永定河水系
湖白河水系
北运河水系
蓟运河水系
大清河水系
水资源量
3.54
2005年北京市水资源统计图(单位:亿)
图1 不同旋钮位置示意图
图3 煤气流量和烧开一壶水所需时间关系
图2 煤气流量和烧开一壶水所需煤气量关系图
图2煤气流量和烧开一壶水所需煤气量关系图
图3煤气流量和烧开一壶水所需时间关系图
图7
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
冲刺 中考数学 应用题怎样解
题型1?方程(组)型应用题
方程是描述丰富多彩的现实世界数量关系的最重要的语言,也是中考命题所要考察的重点热点之一。我们必须广泛了解现代社会中日常生活、生产实践、经济活动的有关常识。并学会用数学中方程的思想去分析和解决一些实际问题。解此类问题的方法是:(1)审题,明确未知量和已知量;(2)设未知数,务必写明意义和单位;(3)依题意,找出等量关系,列出等量方程;(4)解方程,必要时验根。
题型2?不等式(组)型应用题
现实世界中不等关系是普遍存在的,许多现实问题很难确定(有时也不需要确定)具体的数值。但可以求出或确定这一问题中某个量的变化范围(趋势),从而对所有研究问题的面貌有一个比较清楚的认识。本节中,我们所要讨论的问题大多是要求出某个量的取值范围或极端可能性,它们涉及我们日常生活中的方方面面。
列不等式时要从题意出发,设好未知量之后,用心体会题目所规定的实际情境,从中找出不等关系。
题型3?函数型应用问题
函数及其图象是初中数学中的主要内容之一,也是初中数学与高中数学相联系的纽带。它与代数、几何、三角函数等知识有着密切联系,中考命题中既重点考查函数及其图象的有关基础知识,同时以函数为背景的应用性问题也是命题热点之一,多数省市作压轴题。因此,在中考复习中,关注这一热点显得十分重要。解这类题的方法是对问题的审读和理解,掌握用一个变量的代数式表示另一个变量,建立两个变量间的等量关系,同时从题中确定自变量的取值范围。
题型4?统计型应用问题
统计的内容有着非常丰富的实际背景,其实际应用性特别强。中考试题的热点之一,就是考查统计思想方法,同时考查学生应用数学的意识和处理数据解决实际问题的能力。
题型5?几何型应用问题
几何应用题常常以现实生活情景为背景,考查学生识别图形的能力、动手操作图形的能力、运用几何知识解决实际问题的能力以及探索、发现问题的能力和观察、想像、分析、综合、比较、演绎、归纳、抽象、概括、类比、分类讨论、数形结合等数学思想方法。
例1.(2007天津市)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程。如果你选用其他的解题方案,此时,不必填写表格,只需按照解答题的一般要求,进行解答即可。
甲乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时。问二人每小时各走几千米?
(1)设乙每小时走x千米,根据题意,利用速度、时间、路程之间的关系填写下表。
(要求:填上适当的代数式,完成表格)
(2)列出方程(组),并求出问题的解。
解:(1)
(2)根据题意,列方程得
整理得
解这个方程得
经检验,都是原方程的根。但速度为负数不合题意
所以只取,此时
答:甲每小时走6千米,乙每小时走5千米。
例2.(2007乌兰察布盟)某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元。
(1) 求A、B两种品牌的化妆品每套进价分别为多少元?
(2) 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
解:(1)设A种品牌的化妆品每套进价为x元,B种品牌的化妆品每套进价为y元,得
解得
答:A、B两种品牌得化妆品每套进价分别为100元,75元。
(2)设A种品牌得化妆品购进m套,则B种品牌得化妆品购进(2m+4)套。
根据题意得:解得
∵m为正整数,∴m=16、17、18 ∴2m+4=36、38、40
答:有三种进货方案
(1) A种品牌得化妆品购进16套,B种品牌得化妆品购进36套。
(2) A种品牌得化妆品购进17套,B种品牌得化妆品购进38套。
A种品牌得化妆品购进18套,B种品牌得化妆品购进40套。
例3.(2007扬州)连接上海市区到浦东国际机场的磁悬浮轨道全长约为,列车走完全程包含启动加速、匀速运行、制动减速三个阶段.已知磁悬浮列车从启动加速到稳定匀速动行共需秒,在这段时间内记录下下列数据:
时间(秒) 0 50 100 150 200
速度(米/秒) 0 30 60 90 120
路程(米) 0 750 3000 6750 12000
(1)请你在一次函数、二次函数和反比例函数中选择合适的函数来分别表示在加速阶段()速度与时间的函数关系、路程与时间的函数关系.
(2)最新研究表明,此种列车的稳定动行速度可达180米/秒,为了检测稳定运行时各项指标,在列车达到这一速度后至少要运行100秒,才能收集全相关数据.若在加速过程中路程、速度随时间的变化关系仍然满足(1)中的函数关系式,并且制作减速所需路程与启动加速的路程相同.根据以上要求,至少还要再建多长轨道就能满足试验检测要求?
(3)若减速过程与加速过程完全相反.根据对问题(2)的研究,直接写出列车在试验检测过程中从启动到停车这段时间内,列车离开起点的距离(米)与时间(秒)的函数关系式(不需要写出过程)
解:(1)通过描点或找规律,确定与是一次函数,
与是二次函数,.
(2)由得当时,秒,则米千米.
米千米
因为减速所需路程和启动加速路程相同,所以总路程为
所以还需建千米.
(3)当时,
当时,
当时,(一般式为).
例4、(2007北京市)根据北京市水务局公布的2004年、2005年北京市水资源和用水情况的相关数据,绘制如下统计图表:
2005年北京市水资源分布图(单位:亿) 2004年北京市用水量统计图
2005年北京市用水情况统计表
生活用水 环境用水 工业用水 农业用水
用水量(单位:亿) 13.38 6.80 13.22
占全年总用水量的比例
(1)北京市水资源全部由永定河水系、潮白河水系、北运河水系、蓟运河水系、大清河水系提供.请你根据以上信息补全2005年北京市水资源统计图,并计算2005年全市的水资源总量(单位:亿);
(2)在2005年北京市用水情况统计表中,若工业用水量比环境用水量的6倍多0.2亿,请你先计算环境用水量(单位:亿),再计算2005年北京市用水总量(单位:亿);
(3)根据以上数据,请你计算2005年北京市的缺水量(单位:亿);
(4)结合2004年及2005年北京市的用水情况,谈谈你的看法.
解:(1)初全2005年北京市水资源统计图见右图;
水资源总量为亿.
(2)设2005年环境用水量为亿.
依题意得.
解得.
所以2005年环境用水量为亿.
因为,
所以2005年北京市用水总量为亿.
(3)因为,所以2005年北京市缺水量为亿.
(4)说明:通过对比2004年及2005年北京市的用水情况,能提出积极看法的给分.
例5、(2007荆门市)一、问题背景
某校九年级(1)班课题学习小组对家庭煤气的使用量做了研究,其实验过程和对数据的处理如下.
仔细观察现在家庭使用的电子打火煤气灶,发现当关着煤气的时候,煤气旋钮(以下简称旋钮)的位置为竖起方向,把这个位置定为0°,煤气开到最大时,位置为90°.(以0°位置作起始边,旋钮和起始边的夹角).在0~90°之间平均分成五等分,代表不同的煤气流量,它们分别是18°,36°,54°,72°,90°,见图1.
位置 烧开一壶水所需 流量
时间(分) 煤气量(m3) m3/分
18° 19 0.13 0.0068
36° 16 0.12 0.0076
54° 13 0.14 0.0107
72° 12 0.15 0.0124
90° 10 0.17 0.0172
在这些位置上分别以烧开一壶水(3.75升)为标准,记录所需的时间和所用的煤气量.并根据旋钮位置以及烧开一壶水所需时间(用t表示)、所用煤气量(用v表示),计算出不同旋钮位置所代表的煤气流量(用L表示),L=v/t,数据见右表.这样为可以研究煤气流量和烧开一壶水所需时间及用气量之间的关系了.
二、任务要求
1.作图:将下面图2中的直方图补充完整;在图3中作出流量与时间的折线图.
2.填空:①从图2可以看出,烧开一壶水所耗用的最少煤气量为_______m2,此时旋钮位置在______.
②从图3可以看出,不考虑煤气用量,烧开一壶水所用的最短时间为_______分钟,此时旋钮位置在______.
3.通过实验,请你对上述结果(用煤气烧水最省时和最省气)作一个简要的说明.
解:(1)(每图2分)…………………………………………………………………………4分
(2)0.12,36°;10,90°;(每空一分)………………………………………………………8分
(3)当旋钮开到36°附近时最省气,当旋钮开到90°时最省时.最省时和最省气不可能同时做到.………………………………………………………………………………………10分
说明:第(3)问只要表达意思明确即可,方式和文字不一定如此表达.
注:最省气的旋钮位置在36°附近,接近0°~90°的黄金分割点0.382(=0.4).
例6、(2007资阳)一座建于若干年前的水库大坝的横断面如图7所示,其中背水面的整个坡面是长为90米、宽为5米的矩形. 现需将其整修并进行美化,方案如下:① 将背水坡AB的坡度由1∶0.75改为1∶;② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花 .
⑴ 求整修后背水坡面的面积;
⑵ 如果栽花的成本是每平方米25元,种草的成本是每平方米20元,那么种植花草至少需要多少元?
解:⑴ 作AE⊥BC于E.
∵ 原来的坡度是1∶0.75,∴ = .
设AE=4k,BE=3k,∴ AB=5k,又 ∵ AB=5米,∴k=1,则AE=4米 .
设整修后的斜坡为,由整修后坡度为1∶,有
,∴∠=30°,
∴ 8米 . ∴ 整修后背水坡面面积为90×8=720米2 .
⑵ 将整修后的背水坡面分为9块相同的矩形,则每一区域的面积为80米2 .
解法一:∵ 要依次相间地种植花草,有两种方案:
第一种是种草5块,种花4块,需要20×5×80+25×4×80=16000元;
第二种是种花5块,种草4块,需要20×4×80+25×5×80=16400元 .
∴ 应选择种草5块、种花4块的方案,需要花费16000元 .
解法二:∵ 要依次相间地种植花草,则必然有一种是5块,有一种是4块,而栽花的成本是每平方米25元,种草的成本是每平方米20元,
∴ 两种方案中,选择种草5块、种花4块的方案花费较少 .
即:需要花费20×5×80+25×4×80=16000元 .
6.78
3.22
6.88
2.79
3.51
潮白河水系
永定河水系
蓟运河水系
北运河水系
永定河水系
大清河水系
农业用水
生活用水
工业用水
环境用水
0
1
2
3
4
5
6
7
8
水系
2.79
6.78
6.88
3.22
永定河水系
潮白河水系
北运河水系
蓟运河水系
大清河水系
水资源量
2005年北京市水资源统计图(单位:亿)
0
1
2
3
4
5
6
7
8
水系
2.79
6.78
6.88
3.22
永定河水系
湖白河水系
北运河水系
蓟运河水系
大清河水系
水资源量
3.54
2005年北京市水资源统计图(单位:亿)
图1 不同旋钮位置示意图
图3 煤气流量和烧开一壶水所需时间关系
图2 煤气流量和烧开一壶水所需煤气量关系图
图2煤气流量和烧开一壶水所需煤气量关系图
图3煤气流量和烧开一壶水所需时间关系图
图7
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
