八年级数学期末复习大串讲+练专题五 《全等三角形》考点知识梳理专题训练
文档属性
| 名称 | 八年级数学期末复习大串讲+练专题五 《全等三角形》考点知识梳理专题训练 |  | |
| 格式 | doc | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 20:17:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学上期末大串讲+练专题复习
专题五 《全等三角形》考点知识梳理专题训练
知识点归纳
知识点 1: 全等图形
全等形:能够完全重合的两个图形叫做全等形。
(一)全等形的形状相同,大小相等,与图形所在的位置无关。
(二)两个全等形的面积一定相等,但面积相等的两个图形不一定是全等形。
(三)一个图形经过平移、翻折、旋转后,形状、大小都没有改变,只是位置发生了变化,即平移、翻折、旋转前后的图形全等。
知识点2:全等多边形
(1)定义:能够完全重合的两个多边形叫做全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
(2)性质:全等多边形的对应边相等,对应角相等.
(3)判定:边、角分别对应相等的两个多边形全等.
知识点3: 全等三角形
(一)全等三角形:能够完全重合的两个三角形叫做全等三角形。
(二)全等三角形中的对应元素
1、概念:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应顶点:点A与点D,点B与点E,点C与点F。对应边:AB与DE,AC与DF,BC与EF。对应角:∠A与∠D,∠B与∠E,∠C与∠F。
2、对应元素的确定方法
(1)字母顺序确定法∶根据书写规范,按照对应顶点确定对应边、对应角。
(2)图形位置确定法
①公共边一定是对应边;
②公共角一定是对应角;
③对顶角一定是对应角;
(3)图形大小确定法∶两个全等三角形的最大的边(角)是对应边(角),最小的边(角)是对应边(角)。
(三)全等三角形的表示:全等用符号“≌”表示,读作“全等于”。如三角形△ABC和△DEF全等,记作△ABC≌△DEF。记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
知识点4 :全等三角形的性质
(一)全等三角形的对应边相等,全等三角形的对应角相等。
(二)全等三角形对应边上的高、中线分别相等,对应角的平分线相等,面积相等,周长相等。
∵△ABC≌△DEF∴AB=DE,AC=DF,BC=EF(全等三角形的对应边相等)。∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)。
知识点 5 判定全等三角形(边边边)
1、三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
知识点6 判定全等三角形(边角边)
1、用直尺和圆规作一个角等于已知角(已知角∠AOB,求作∠AOB=∠A'O'B')
①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D。
②画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C'。
③以点C'为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D';
④过点D'画射线O'B',则∠A'O'B'=∠AOB。
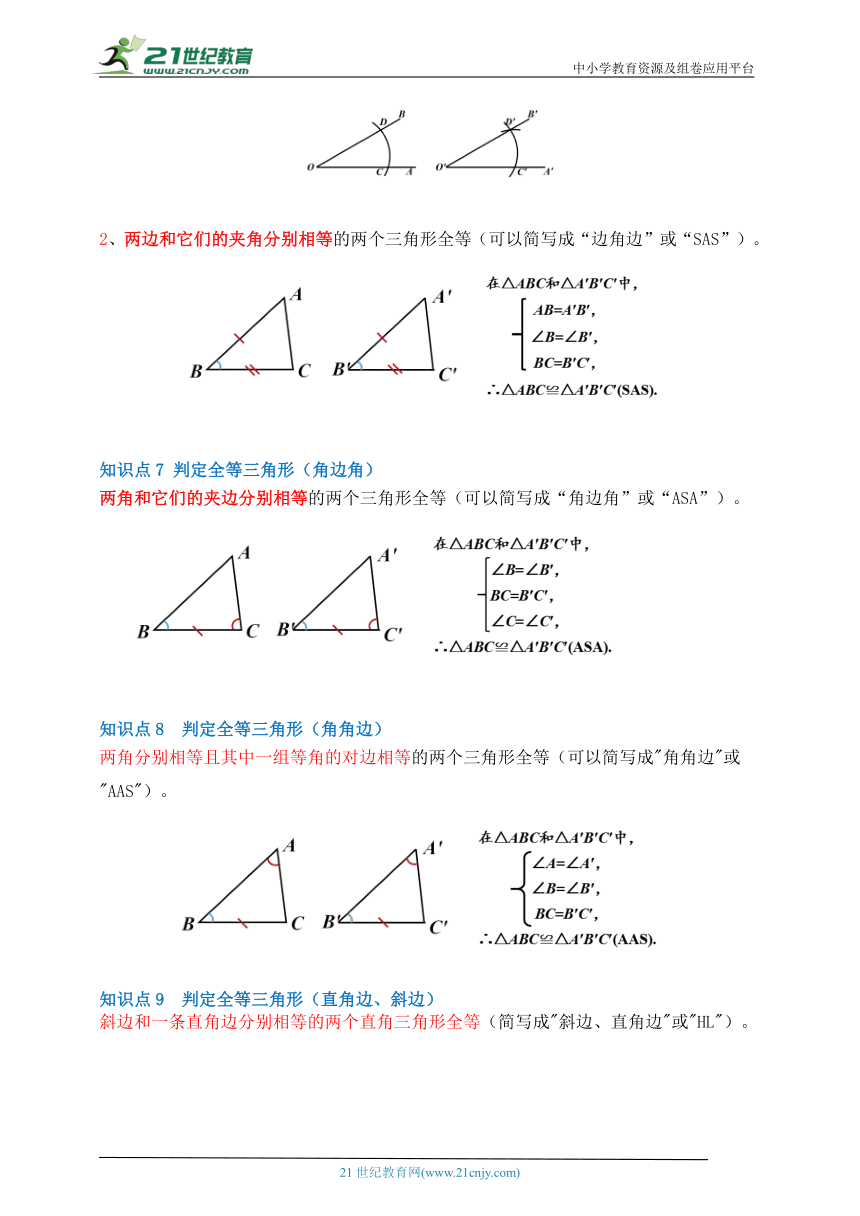
2、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)。
知识点7 判定全等三角形(角边角)
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
知识点8 判定全等三角形(角角边)
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成"角角边"或"AAS")。
知识点9 判定全等三角形(直角边、斜边)
斜边和一条直角边分别相等的两个直角三角形全等(简写成"斜边、直角边"或"HL")。
注意:用“HL”证明两个直角三角形全等,书写时两个三角形符号前面要加上“Rt”。
知识点10 角的平分线的性质
(一)作已知角的平分线(已知:∠AOB。求作:∠AOB的平分线)
1、以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N。
2、分别以M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C。
3、画射线OC,射线OC即为所求。
(二)角的平分线的性质:角的平分线上的点到角的两边的距离相等。
几何表示:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E。∴PD=PE。
知识点11 角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上。
几何表示:
∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,
∴点P在∠AOB的平分线OC上。
重要拓展:
1、三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等。反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点。
2、三角形的角平分线与三角形一边交于一点,这条角平分线把三角形分成两个小三角形,它们的面积比等于另外两边的长度的比。
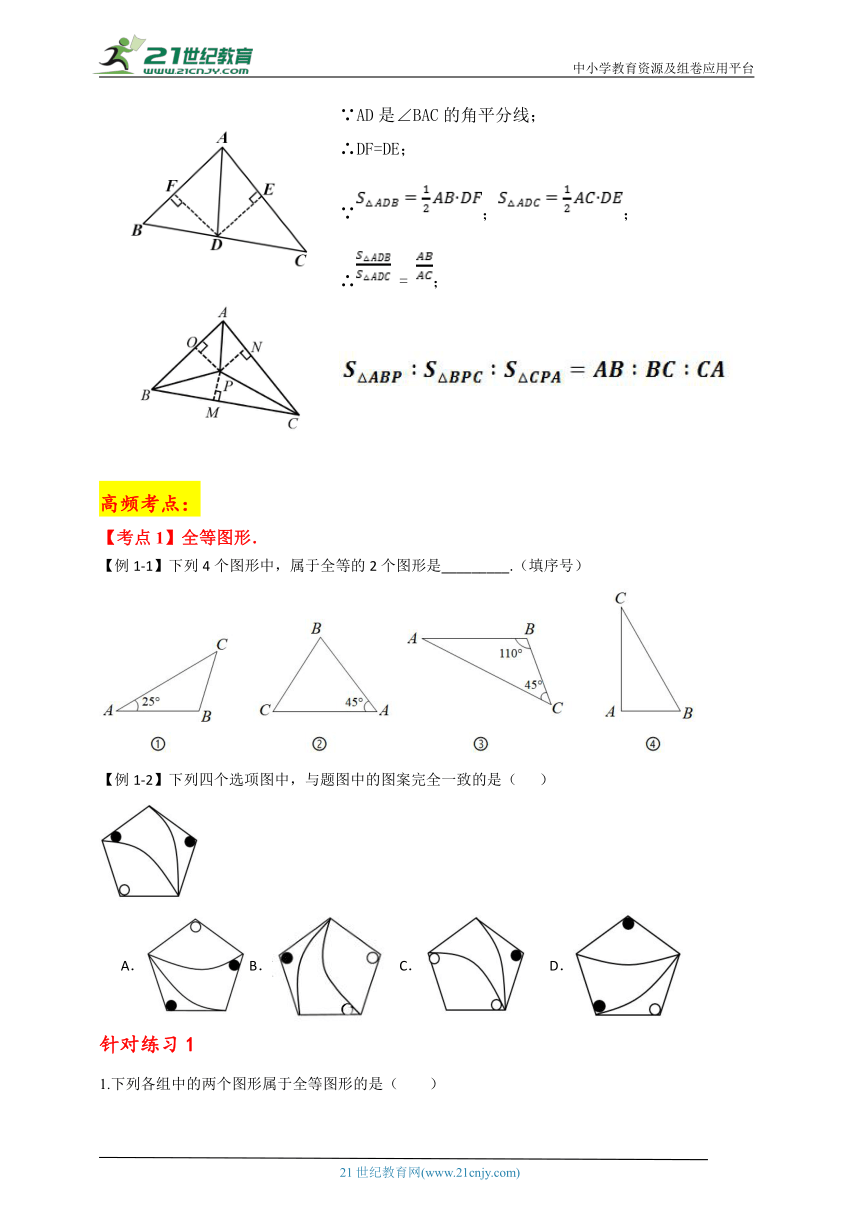
∵AD是∠BAC的角平分线;∴DF=DE;∵;;∴ = ;
高频考点:
【考点1】全等图形.
【例1-1】下列4个图形中,属于全等的2个图形是_________.(填序号)
【例1-2】下列四个选项图中,与题图中的图案完全一致的是( )
A. B. C. D.
针对练习1
1.下列各组中的两个图形属于全等图形的是( )
B.
C. D.
2.下列说法正确的是( )
A.两个形状相同的图形称为全等图形
B.两个圆是全等图形
C.全等图形的形状、大小都相同
D.面积相等的两个三角形是全等图形
3 .如图,四边形ABCD≌四边形A'B'C'D',则∠A的度数是 °.
【考点2】全等三角形的性质.
【例2-1】下列说法中,正确的有( )
①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等,面积相等 ④若,则,
A.1个 B.2个 C.3个 D.4个
【例2-2】如图,△ABC≌△DEC,点E在AB上,AC与DE相交于点F,∠BCE=40°.则∠AED的度数为( )
A.40° B.50° C.60° D.70°
【例2-3】如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为 .
针对练习2
1 .若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
2 .如图,图形的各个顶点都在3×3正方形网格的格点上,则∠1+∠2=( )
A.60° B.72° C.45° D.90°
3.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为( )
A.10 B.12 C.14 D.16
【考点3】全等三角形的判定
【例3-1】如图,点在一条直线上,,求证:.
【例3-2】如图,在中,D是延长线上一点,满足,过点C作,且,连接并延长,分别交,于点F,G.
(1)求证:;
(2)若,,求的长度.
【例3-3】如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
【例3-4】如图,∠A=∠D=90°,添加下列条件中的一个后,能判定△ABC与△DCB全等的有( )
①∠ABC=∠DCB;
②∠ACB=∠DBC;
③AB=DC;
④AC=DB.
A.1个 B.2个 C.3个 D.4个
针对练习3
1.如图,已知点是线段上一点,,.
(1)求证:;
(2)求证:.
2 .如图,,,连接交于点O,点E,F在线段上,且.求证:.
3 .已知:如图,、是的高,且.求证:.
4.如图,,和是对应角.在中,是最长边.在中,是最长边,,,.
(1)写出其他对应边及对应角;
(2)求线段及线段的长度.
【考点4】全等三角形的判定与性质
【例4-1】如图,AB=AC,AD=AE,∠BAC=∠DAE,点B,D,E在同一直线上,若∠1=25°,∠2=35°,则∠3的度数是( )
A.50° B.55° C.60° D.70°
【例4-2】如图,在平面直角坐标系中,△ABC的顶点A(3,0),B(0,﹣1),点C在第四象限,且AB=BC,∠ABC=90°,则点C的坐标是( )
A.(﹣4,1) B.(1,﹣4) C.(﹣1,4) D.(4,﹣1)
【例4-3】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
针对练习4
1.如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O.
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠A=51°,求∠BOF的度数.
2 .如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
3 .如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
如图,CD=BE,∠C=∠B,∠1=∠2.
(1)求证:△ABE≌△ACD.
(2)若ME=5,求DN的长度.
【考点5】全等三角形的应用
【例5-1】如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
【例5-2】如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5米,则槽宽为( )
A.3 B.4 C.5 D.6
【例5-3】如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
针对练习5
1 .如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
2 如图,某人将一块三角形玻璃打碎成两块,带 ② 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
3 .王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
【考点6】角平分线的性质
【例6-1】如图,已知,射线平分,过点E作于点H,作于点F,并延长交于点G,连接.若,则的长为 .
【例6-2】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长( )
A.3cm B.4cm C.5cm D.6cm
【例6-3】如图,中,,的平分线交于点D,若,则点D到的距离是 cm.
针对练习6
如图,已知△ABC的周长是18,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则△ABC的面积是( )
A.6 B.9 C.18 D.36
2 .如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.5:3:2 C.2:3:4 D.3:4:5
3.如图,AD∥BC,∠D=90°,∠CPB=30°,∠DAB的角平分线与∠CBA的角平分线相交于点P,且D,P,C在同一条直线上.
(1)求∠PAD的度数;
(2)求证:P是线段CD的中点.
【考点7】角平分线的判定
【例7-1】如图,A、B两点分别在射线OM,ON上,点C在∠MON的内部,且AC=BC,CD⊥OM,CE⊥ON,垂足分别为D,E,且AD=BE.
(1)求证:OC平分∠MON;
(2)若AD=3,BO=4,求AO的长.
【例7-2】如图,已知垂足为,垂足为,,.
(1)求证:平分;
(2)丁丁同学观察图形后得出结论:,请你帮他写出证明过程.
【例7-3】已知:如图,在中,,D是上一点,于E,且.
(1)求证:平分;
(2)若,求的度数.
针对练习7
1 .如图,在中,的平分线与的外角平分线交于点,于点,于点.
(1)若,求点到直线的距离;
(2)求证:点在的平分线上.
2.求证:三角形两外角的平分线的交点到三角形三边(或所在的直线)距离相等.
要求:画图,写出已知,求证,然后写出证明过程.
【考点8】尺规作图:(1)作一个角等于已知角(2)作已知角的平分线
【例8-1】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.
已知:如图,直线和直线外一点.
求作:直线,使直线直线.
作法:如图,
①在直线上任取一点,作射线;
②以为圆心,为半径作弧,交直线于点,连接;
③以为圆心,长为半径作弧,交射线于点;分别以为圆心,大于长为半径作弧,在的右侧两弧交于点;
④作直线;
所以直线就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知平分,
.
又,
.(_______________________________)(填依据1).
,
.
,∴直线直线.(______________________)(填依据2).
【例8-2】如图,已知锐角,.
(1)尺规作图:求作的角平分线;(保留作图痕迹,不写作法)
(2)点在边上且,请连接,求证:.
针对练习8
1.如图,在中,,观察图中尺规作图的痕迹,则的度数为( )
A. B. C. D.
2.如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=( )
A.2 B.3 C.4 D.5
八年级数学上期末大串讲+练专题复习
专题五 《全等三角形》考点知识梳理专题训练
知识点归纳
知识点 1: 全等图形
全等形:能够完全重合的两个图形叫做全等形。
(一)全等形的形状相同,大小相等,与图形所在的位置无关。
(二)两个全等形的面积一定相等,但面积相等的两个图形不一定是全等形。
(三)一个图形经过平移、翻折、旋转后,形状、大小都没有改变,只是位置发生了变化,即平移、翻折、旋转前后的图形全等。
知识点2:全等多边形
(1)定义:能够完全重合的两个多边形叫做全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
(2)性质:全等多边形的对应边相等,对应角相等.
(3)判定:边、角分别对应相等的两个多边形全等.
知识点3: 全等三角形
(一)全等三角形:能够完全重合的两个三角形叫做全等三角形。
(二)全等三角形中的对应元素
1、概念:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应顶点:点A与点D,点B与点E,点C与点F。对应边:AB与DE,AC与DF,BC与EF。对应角:∠A与∠D,∠B与∠E,∠C与∠F。
2、对应元素的确定方法
(1)字母顺序确定法∶根据书写规范,按照对应顶点确定对应边、对应角。
(2)图形位置确定法
①公共边一定是对应边;
②公共角一定是对应角;
③对顶角一定是对应角;
(3)图形大小确定法∶两个全等三角形的最大的边(角)是对应边(角),最小的边(角)是对应边(角)。
(三)全等三角形的表示:全等用符号“≌”表示,读作“全等于”。如三角形△ABC和△DEF全等,记作△ABC≌△DEF。记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
知识点4 :全等三角形的性质
(一)全等三角形的对应边相等,全等三角形的对应角相等。
(二)全等三角形对应边上的高、中线分别相等,对应角的平分线相等,面积相等,周长相等。
∵△ABC≌△DEF∴AB=DE,AC=DF,BC=EF(全等三角形的对应边相等)。∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)。
知识点 5 判定全等三角形(边边边)
1、三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
知识点6 判定全等三角形(边角边)
1、用直尺和圆规作一个角等于已知角(已知角∠AOB,求作∠AOB=∠A'O'B')
①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D。
②画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C'。
③以点C'为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D';
④过点D'画射线O'B',则∠A'O'B'=∠AOB。
2、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)。
知识点7 判定全等三角形(角边角)
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
知识点8 判定全等三角形(角角边)
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成"角角边"或"AAS")。
知识点9 判定全等三角形(直角边、斜边)
斜边和一条直角边分别相等的两个直角三角形全等(简写成"斜边、直角边"或"HL")。
注意:用“HL”证明两个直角三角形全等,书写时两个三角形符号前面要加上“Rt”。
知识点10 角的平分线的性质
(一)作已知角的平分线(已知:∠AOB。求作:∠AOB的平分线)
1、以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N。
2、分别以M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C。
3、画射线OC,射线OC即为所求。
(二)角的平分线的性质:角的平分线上的点到角的两边的距离相等。
几何表示:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E。∴PD=PE。
知识点11 角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上。
几何表示:
∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,
∴点P在∠AOB的平分线OC上。
重要拓展:
1、三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等。反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点。
2、三角形的角平分线与三角形一边交于一点,这条角平分线把三角形分成两个小三角形,它们的面积比等于另外两边的长度的比。
∵AD是∠BAC的角平分线;∴DF=DE;∵;;∴ = ;
高频考点:
【考点1】全等图形.
【考点1】全等图形.
【例1-1】下列4个图形中,属于全等的2个图形是_________.(填序号)
【答案】①③
【分析】先求出的度数,然后分析求解即可.
【详解】解:在③中,,
∴与①中的相等,并且两夹边对应相等,
∴属于全等的2个图形是①③
故答案为①③.
【点评】本题考查了三角形全等的条件,熟悉全等三角形的判定定理是解题的关键.
【例1-2】下列四个选项图中,与题图中的图案完全一致的是( )
A. B. C. D.
【答案】A
【分析】根据全等形是能够完全重合的两个图形进行分析判断.
【详解】解:将原图绕其中心顺时针旋转144度后,可以和A中的图形重合;
原图通过旋转变换不能得到与B、C、D中的图形重合,
故选:A.
【点睛】本题考查的是全等形的识别,通过旋转找出原图与选项中的图形重合是解题的关键。
针对练习1
1.下列各组中的两个图形属于全等图形的是( )
B.
C. D.
【答案】B
【分析】根据全等图形的定义,逐一判断选项,即可.
【详解】解:A、两个图形不能完全重合,不属于全等图形,故此选项不符合题意;
B、两个图形能完全重合,属于全等图形,故此选项符合题意;
C、两个图形不能完全重合,不属于全等图形,故此选项不符合题意;
D、两个图形不能完全重合,不属于全等图形,故此选项不符合题意.
故选:B.
【点评】本题主要考查全等图形的定义,熟练掌握“能完全重合的两个图形,是全等图形”是解题的关键.
2.下列说法正确的是( )
A.两个形状相同的图形称为全等图形
B.两个圆是全等图形
C.全等图形的形状、大小都相同
D.面积相等的两个三角形是全等图形
【答案】C
【解答】解:A、两个形状相同、大小相同的图形是全等图形,故原命题错误,不符合题意;
B、两个圆的形状相同但大小不相同,不是全等图形,故原命题错误,不符合题意;
C、全等图形的形状、大小都相同,正确,符合题意;
D、面积相等的两个三角形不一定是全等图形,故原命题错误,不符合题意.
故选:C.
3 .如图,四边形ABCD≌四边形A'B'C'D',则∠A的度数是 °.
【答案】95.
【分析】利用相似多边形对应角相等即可求解.
【解答】解:∵四边形ABCD∽四边形A′B′C′D′,
∴∠D=∠D′=130°,
∴∠C′=360°﹣130°﹣60°﹣75°=95°
∴∠α=∠C′=95°,
故答案为:95.
【考点2】全等三角形的性质.
【例2-1】下列说法中,正确的有( )
①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等,面积相等 ④若,则,
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】根据全等的定义和性质判断即可.
【详解】①形状大小都相同的两个图形是全等形,故①错误;
②面积相等的两个图形不一定是全等形,故②错误;
③全等三角形的周长相等,面积相等,是对的,故③正确;
④若,则,,故④错误;
故正确的有1个.
故选:A
【点睛】此题考查全等三角形的定义和性质,解题关键是掌握全等三角形的定义.
【例2-2】如图,△ABC≌△DEC,点E在AB上,AC与DE相交于点F,∠BCE=40°.则∠AED的度数为( )
A.40° B.50° C.60° D.70°
【答案】A
【分析】由△ABC≌△DEC,得∠DEC=∠B=73°,BC=EC,再求出∠CEB=∠B,最后根据平角的性质即可得答案.
【解答】解:∵△ABC≌△DEC,
∴BC=EC,∠CED=∠B,
∴∠CEB=∠B,
∵∠BCE=40°,
∴∠CEB=∠B==70°,
∴∠AED=180°﹣∠DEC﹣∠CEB=180°﹣70°﹣70°=40°,
故选:A.
【例2-3】如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为 .
【答案】 或 或(-1,3)
【解析】【解答】解:因为 与 的一条边 重合
当点D在 的下方时,满足条件的坐标有 和 ;
当点D在 的上方时,满足条件的坐标是 .
故满足条件的为 或 或(-1,3)
针对练习2
1 .若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
【答案】A
【分析】直接利用全等三角形的性质得出对应边相等进而得出答案.
【解答】解:∵△ABC≌△DEF,
∴BC=EF=30,
故选:A.
2 .如图,图形的各个顶点都在3×3正方形网格的格点上,则∠1+∠2=( )
A.60° B.72° C.45° D.90°
【答案】C
【解答】解:如图所示,∵AB=AD=1,BC=DE=2,∠ABC=∠ADE=90°,
∴△ABC≌△ADE(SAS),
∴∠AED=∠1,
∴∠1+∠2=∠2+∠AED=∠BEF,
∵EF=BF=1,∠BFE=90°,
∴∠BEF=45°,
∴∠1+∠2=∠BEF=45°.
故选:C.
3.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为( )
A.10 B.12 C.14 D.16
【答案】C
【分析】由全等三角形的性质得出△DOC的周长为10,进而得出△DBC的周长=△DOC的周长+BC即可.
【解答】解:∵△AOB≌△DOC,△AOB的周长为10,
∴△DOC的周长为10,OB=OC,
∴△DBC的周长=DO+OB+DC+BC
=DO+OC+DC+BC
=△DOC的周长+BC
=10+4
=14.
故选:C.
【考点3】全等三角形的判定
【例3-1】如图,点在一条直线上,,求证:.
【答案】见解析
【分析】根据题意,运用“边边边”的方法证明三角形全等.
【详解】证明:∵,
∴,即,
在和中
∴.
【点睛】本题主要考查三角形全等的判定,掌握全等三角形的判定方法解题的关键.
【例3-2】如图,在中,D是延长线上一点,满足,过点C作,且,连接并延长,分别交,于点F,G.
(1)求证:;
(2)若,,求的长度.
【答案】(1)见解析
(2)4
【分析】(1)根据证明即可;
(2)根据全等三角形的性质解答即可.
【详解】(1)∵,
∴,
在与中,
,
∴;
(2)∵,
∴,
∵,
∴,
∵,
∴
∴.
【点睛】此题考查全等三角形的判定和性质,关键是掌握全等三角形的判定和性质.
【例3-3】如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
【答案】D
【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出即可.
【解答】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:D.
【例3-4】如图,∠A=∠D=90°,添加下列条件中的一个后,能判定△ABC与△DCB全等的有( )
①∠ABC=∠DCB;
②∠ACB=∠DBC;
③AB=DC;
④AC=DB.
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】根据题意和图形,可以得到∠A=∠D=90°,BC=CB,然后根据各个选项中的条件,结合全等三角形的判定定理即可求解.
【解答】解:①添加条件∠ABC=∠DCB,又∠A=∠D=90°,BC=CB,由AAS能判定△ABC与△DCB全等,故①符合题意;
②添加条件∠ACB=∠DBC,又∠A=∠D=90°,BC=CB,由AAS能判定△ABC与△DCB全等,故②符合题意;
③添加条件AB=DC,又∠A=∠D=90°,BC=CB,由HL能判定△ABC与△DCB全等,故③符合题意;
④添加条件AC=DB,又∠A=∠D=90°,BC=CB,由HL能判定△ABC与△DCB全等,故④符合题意.
故选:D.
针对练习3
1.如图,已知点是线段上一点,,.
(1)求证:;
(2)求证:.
【答案】(1)见解析
(2)见解析
【分析】(1)由得,即,从而即可证得;
(2)由可得,,即可得到,从而即可得证.
【详解】(1)证明:,
,
,
在和中,
,
;
(2)解:,
,,
,
.
【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
2 .如图,,,连接交于点O,点E,F在线段上,且.求证:.
【分析】利用已知条件证明,推出,由,得到,即.
【详解】证明:∵,
∴,
在和中,,
∴,
∴,
∵,
∴,
即.
【点睛】此题考查全等三角形的性质与判定,解题的关键是证明.
3 .已知:如图,、是的高,且.求证:.
【分析】根据、是的高得到直角,再证明≌即可得到结论.
【详解】证明:、是的高,
,,
,
在和中,
,
≌,
.
【点睛】本题考查全等三角形的性质和判定,利用证明直角三角形全等是本题关键.
4.如图,,和是对应角.在中,是最长边.在中,是最长边,,,.
(1)写出其他对应边及对应角;
(2)求线段及线段的长度.
【答案】(1)对应边:和,和;对应角:和,和.
(2),
【分析】(1)由和是对应角可知F和M点是对应点,结合最长边对应关系可知和相对应,再由对应边所对的角也是对应关系可知和是对应角,据此进行逐一判断即可;
(2)由(1)所得对应关系可知,,由,可得.
【详解】(1)解:对应边:和,和;对应角:和,和.
(2)∵,
∴,,
∵,
∴.
【点睛】本题考查了全等三角形的性质,熟练掌握全等三角形的对应边相等,对应角相等是解题的关键.
【考点4】全等三角形的判定与性质
【例4-1】如图,AB=AC,AD=AE,∠BAC=∠DAE,点B,D,E在同一直线上,若∠1=25°,∠2=35°,则∠3的度数是( )
A.50° B.55° C.60° D.70°
【答案】C
【分析】先证明△BAD≌△CAE(SAS),根据全等三角形的性质可得∠1=∠ABD,再根据外角的性质,即可求出∠3.
【解答】解:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠1=∠ABD,
∵∠1=25°,∠2=35°,
∴∠3=∠2+∠ABD=60°,
故选:C.
【例4-2】如图,在平面直角坐标系中,△ABC的顶点A(3,0),B(0,﹣1),点C在第四象限,且AB=BC,∠ABC=90°,则点C的坐标是( )
A.(﹣4,1) B.(1,﹣4) C.(﹣1,4) D.(4,﹣1)
【答案】B
【分析】过点C作CE⊥y轴于E,根据AAS证明△AOB与△BEC全等,进而解答即可.
【解答】解:过点C作CE⊥y轴于E,
∵∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠AOB=90°,
∴∠ABO+∠BAO=90°,
∴∠BAO=∠CBE,
在△AOB与△BEC中,
,
∴△AOB≌△BEC(AAS),
∴OB=EC=1,BE=OA=3,
∴OE=OB+BE=1+3=4,
∴点C坐标(1,﹣4),
故选:B.
【例4-3】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;
(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.
【解答】(1)证明:∵∠BAC=∠FAG,
∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,
∴∠BAD=∠CAG,
在△ABF和△ACG中,
,
∴△ABF≌△ACG(ASA);
(2)证明:∵△ABF≌△ACG,
∴AF=AG,BF=CG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵∠BAD=∠CAG,
∴∠CAD=∠CAG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS).
∴EF=EG,
∴BE=BF+FE=CG+EG.
针对练习4
1.如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O.
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠A=51°,求∠BOF的度数.
【答案】(1)证明见解答;
(2)78°.
【分析】(1)根据HL证明两个三角形全等;
(2)根据三角形全等的性质和三角形外角的性质可得结论.
【解答】(1)证明:∵AE=DB,
∴AE+EB=DB+EB,即AB=DE,
在Rt△ACB和Rt△DFE中,
,
∴Rt△ABC≌Rt△DEF(HL);
(2)解:∵∠C=90°,∠A=51°,
∴∠ABC=∠C﹣∠A=90°﹣51°=39°,
由(1)知Rt△ABC≌Rt△DEF,
∴∠ABC=∠DEF.
∴∠DEF=39°,
∴∠BOF=∠ABC+∠BEF=39°+39°=78°.
2 .如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
【答案】见试题解答内容
【分析】(1)由ASA证明△ABD≌△COD即可;
(2)理由全等三角形的性质即可解决问题;
【解答】(1)证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠BAD+∠B=∠FCD+∠B=90°,
∴∠BAD=∠FCD,
在△ABD和CFD中,
,
∴△ABD≌△CFD(ASA),
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
3 .如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
【答案】见试题解答内容
【分析】(1)根据题意和题目中的条件可以找出△ABC≌△ADE的条件;
(2)根据(1)中的结论和等腰直角三角形的定义可以得到∠FAE的度数;
(3)根据题意和三角形全等的知识,作出合适的辅助线即可证明结论成立.
【解答】证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS);
(2)∵∠CAE=90°,AC=AE,
∴∠E=45°,
由(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°;
(3)延长BF到G,使得FG=FB,
∵AF⊥BG,
∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,
,
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA,
∵∠GCA=∠DCA=45°,
在△CGA和△CDA中,
,
∴△CGA≌△CDA(AAS),
∴CG=CD,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
如图,CD=BE,∠C=∠B,∠1=∠2.
(1)求证:△ABE≌△ACD.
(2)若ME=5,求DN的长度.
【答案】(1)证明见解答;
(2)DN=5.
【分析】(1)根据已知条件利用AAS证明△ABE≌△ACD;
(2)先根据△ABE≌△ACD得出AB=AC,∠E=∠D,再利用ASA证明△ABM≌△ACD,然后得出AM=AN,再证明△ADN≌△AEM,从而得出DN=ME.
【解答】(1)证明∵∠1=∠2,
∴∠BAE=∠CAD,
∵CD=BE,∠C=∠B,
∴△ABE≌△ACD(AAS);
(2)解:∵△ABE≌△ACD,
∴AB=AC,∠E=∠D,
∵∠C=∠B,∠1=∠2,
∴△ABM≌△ACD(ASA),
∴AM=AN,
∵∠DAN=∠EAM,∠E=∠D,
∴△ADN≌△AEM(AAS),
∴DN=ME=5.
【考点5】全等三角形的应用
【例5-1】如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
【分析】先根据BC=EF,AC=DF判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质可知,∠1=∠4,再由直角三角形的两锐角互余即可解答.
【解答】解:∵滑梯、墙、地面正好构成直角三角形,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF(HL),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠ACB+∠DEF=90°.
故选:C.
【例5-2】如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5米,则槽宽为( )
A.3 B.4 C.5 D.6
【分析】连接AB,如图,利用“SAS”证明△OAB≌△OA′B′,从而得到A′B′=AB=5m.
【解答】解:连接AB,如图,
在△OAB和△OA′B′中
∴△OAB≌△OA′B′(SAS),
∴A′B′=AB=5(m).
答:槽宽为5m.
故选:C.
【例5-3】如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
【分析】利用全等三角形的判定方法进行分析即可.
【解答】解:在△ABC和△MBC中,
∴△MBC≌△ABC(ASA),
故选:D.
针对练习5
1 .如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
【分析】根据全等三角形的判定进行判断,注意看题目中提供了哪些证明全等的要素,要根据已知选择判断方法.
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC=90°,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:D.
2 如图,某人将一块三角形玻璃打碎成两块,带 ② 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
【分析】已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.
【解答】解:第①块只保留了原三角形的一个角和部分边,根据这两块中的任一块不能配一块与原来完全一样的;
第②块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带②去.
故答案为:②,ASA.
3 .王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
【分析】根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
【考点6】角平分线的性质
【例6-1】如图,已知,射线平分,过点E作于点H,作于点F,并延长交于点G,连接.若,则的长为 .
【答案】2
【分析】先根据平行线的性质可得,再根据角平分线的定义和“等角的余角相等”可得,再由,可得,由角平分线的性质可得,即可求出的长.
【详解】,
,
即.
,
,
.
∵平分,
,
,
∴平分.
,
.
,
,
∴.
故答案为:2
【点睛】本题主要考查了平行线的性质,角平分线的性质,“等角对等边”.熟练掌握以上知识,且证明平分是解题的关键.
【例6-2】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长( )
A.3cm B.4cm C.5cm D.6cm
【答案】A
【分析】根据角平分线的性质得到DE=DF,根据三角形的面积公式计算即可.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=×AB×DE+×AC×DF=30(cm2),即×13×DE+×7×DF=30,
解得DE=DF=3cm,
故选:A.
【例6-3】如图,中,,的平分线交于点D,若,则点D到的距离是 cm.
【答案】3
【分析】过D作于E.根据角平分线性质求解即可.
【详解】解:过D作于E.如图,
∵是的平分线,,,
∴.
∵,
∴.
故答案为:3.
【点睛】本题主要考查角平分线的性质;作出辅助线是正确解答本题的关键.
针对练习6
如图,已知△ABC的周长是18,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则△ABC的面积是( )
A.6 B.9 C.18 D.36
【答案】C
【分析】由角平分线的性质得到OM=OD=ON,由△ABC的面积=△AOB的面积+△OBC的面积+△OAC的面积,得到△ABC的面积=(AB+BC+AC) OD,由△ABC的周长=18,OD=2,即可求出△ABC的面积=×18×2=18.
【解答】解:过O作OM⊥AB于M,ON⊥AC于N,
∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,
∴OM=OD,ON=OD,
∵△ABC的面积=△AOB的面积+△OBC的面积+△OAC的面积,
∴△ABC的面积=AB OM+BC OD+AC ON=(AB+BC+AC) OD,
∵△ABC的周长=18,OD=2,
∴△ABC的面积=×18×2=18.
故选:C.
2 .如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.5:3:2 C.2:3:4 D.3:4:5
【答案】A
【分析】过点O作OD⊥AB于点D,OE⊥BC于点E,OF⊥AC于点F,根据角平分线的性质定理可知OD=OE=OF.再由三角形的面积公式计算,作比即可.
【解答】解:如图,过点O作OD⊥AB于点D,OE⊥BC于点E,OF⊥AC于点F,
∵点O是△ABC三条角平分线的交点,
∴OD=OE=OF,
∵,
,
,
∴S△OAB:S△OBC:S△OAC=8OD:6OE:4OF=4:3:2.
故选:A.
3.如图,AD∥BC,∠D=90°,∠CPB=30°,∠DAB的角平分线与∠CBA的角平分线相交于点P,且D,P,C在同一条直线上.
(1)求∠PAD的度数;
(2)求证:P是线段CD的中点.
优网版权所有
【答案】(1)30°;
(2)见解答.
【分析】(1)根据平行线的性质得到∠C=180°﹣∠D=90°,∠DAB+∠ABC=180°,再计算出∠PBC=60°,则利用角平分线的定义得到∠ABC=120°,所以∠DAB=60°,然后利用角平分线的定义得到∠PAD的度数;
(2)过P点作PE⊥AB于E点,如图,根据角平分线的性质得到PE=PD,PE=PC,从而得到PD=PC.
【解答】(1)解:∵AD∥BC,
∴∠C=180°﹣∠D=180°﹣90°=90°,
∵∠CPB=30°,
∴∠PBC=90°﹣∠B=60°,
∵PB平分∠ABC,
∴∠ABC=2∠PBC=120°,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠DAB=180°﹣120°=60°,
∵AP平分∠DAB,
∴∠PAD=∠DAB=30°;
(2)证明:过P点作PE⊥AB于E点,如图,
∵AP平分∠DAB,PD⊥AD,PE⊥AB,
∴PE=PD,
∵BP平分∠ABC,PC⊥BC,PE⊥AB,
∴PE=PC,
∴PD=PC,
∴P是线段CD的中点.
【考点7】角平分线的判定
【例7-1】如图,A、B两点分别在射线OM,ON上,点C在∠MON的内部,且AC=BC,CD⊥OM,CE⊥ON,垂足分别为D,E,且AD=BE.
(1)求证:OC平分∠MON;
(2)若AD=3,BO=4,求AO的长.
【分析】(1)根据全等三角形的判定定理推出Rt△ADC≌Rt△BEC,根据全等三角形的性质得出CD=CE,再得出答案即可;
(2)根据全等三角形的性质得出AD=BE=3,根据全等三角形的判定定理推出Rt△ODC≌Rt△OEC,根据全等三角形的性质得出OD=OB,再求出答案即可.
【解答】(1)证明:∵CD⊥OM,CE⊥ON,
∴∠ADC=∠CEB=90°,
在Rt△ADC和Rt△BEC中,
,
∴Rt△ADC≌Rt△BEC(HL),
∴CD=CE,
∵CD⊥OM,CE⊥ON,
∴OC平分∠MON;
(2)解:∵Rt△ADC≌Rt△BEC,AD=3,
∴BE=AD=3,
∵BO=4,
∴OE=OB+BE=4+3=7,
∵CD⊥OM,CE⊥ON,
∴∠CDO=∠CEO=90°,
在Rt△DOC和Rt△EOC中,
,
∴Rt△DOC≌Rt△EOC(HL),
∴OD=OE=7,
∵AD=3,
∴OA=OD+AD=7+3=10.
【例7-2】如图,已知垂足为,垂足为,,.
(1)求证:平分;
(2)丁丁同学观察图形后得出结论:,请你帮他写出证明过程.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)首先用判断出,根据全等三角形的对应边相等得,进而根据到角两边距离相等的点在这个角的角平分线上可得平分;
(2)首先用判断出,根据全等三角形的对应边相等得,结合,根据线段的和差即可得出结论.
【详解】(1)证明:,,
,
在和中,
,
,
,
,,
,
平分;
(2)解:,
在和中
,
,
,
,
.
【点睛】本题考查全等三角形的判定与性质,角平分线的判定定理,能正确根据全等三角形的判定和性质定理进行推理是解此题的关键.
【例7-3】已知:如图,在中,,D是上一点,于E,且.
(1)求证:平分;
(2)若,求的度数.
【答案】(1)见解析
(2)
【分析】(1)根据已知条件结合角平分线判定定理即可证明.
(2)根据直角三角形的两个锐角互余求得度数.
【详解】(1)证明:,,,
点D在的平分线上,
平分.
(2)解:,,
,
平分,
.
【点睛】本题主要考查了角平分线的判定与性质运用,和直角三角形性质的运用,熟练掌握角平分线的判定定理是解答的关键.
针对练习7
1 .如图,在中,的平分线与的外角平分线交于点,于点,于点.
(1)若,求点到直线的距离;
(2)求证:点在的平分线上.
【答案】(1)8cm
(2)见解析
【分析】(1)利用角平分线上一点到角两边距离相等即可求解;
(2)利用如果一点到角的两边距离相等,则这个点在角的角平分线上.
【详解】(1)解:作于,如图,
又∵平分,,
∴,
即点到直线的距离为8cm;
(2)证明:∵平分,且于点,,
∴,
又,
∴,
∴点在的平分线上.
【点睛】本题考查角平分线性质定理以及逆定理,熟练掌握角平分性质的逆用是解决本题的关键。
2.求证:三角形两外角的平分线的交点到三角形三边(或所在的直线)距离相等.
要求:画图,写出已知,求证,然后写出证明过程.
【详解】解;已知:如图,的外角平分线与外角平分线相交于点P.
求证:;
证明:如图,过点P作于F,于G,于H,
∵的外角平分线与相交于点P,
∴,,
∴.
即点P到三边、、所在直线的距离相等
∴三角形两外角的平分线的交点到三角形三边(或所在直线)的距离相等.
【考点8】尺规作图:(1)作一个角等于已知角(2)作已知角的平分线
【例8-1】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.
已知:如图,直线和直线外一点.
求作:直线,使直线直线.
作法:如图,
①在直线上任取一点,作射线;
②以为圆心,为半径作弧,交直线于点,连接;
③以为圆心,长为半径作弧,交射线于点;分别以为圆心,大于长为半径作弧,在的右侧两弧交于点;
④作直线;
所以直线就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知平分,
.
又,
.(_______________________________)(填依据1).
,
.
,∴直线直线.(______________________)(填依据2).
【答案】(1)作图见解析;(2)等边对等角;同位角相等,两直线平行
【解析】解:(1)根据题中画图过程可得:
如图,PQ即为所作图形;
(2)由作图可知平分,
.
又,
.(等边对等角).
,
.
,
∴直线直线.(同位角相等,两直线平行).
【点评】本题考查了尺规作图,等腰三角形的性质,平行线的判定,解题的关键是根据题意作图,然后再进行推理论证.
【例8-2】如图,已知锐角,.
(1)尺规作图:求作的角平分线;(保留作图痕迹,不写作法)
(2)点在边上且,请连接,求证:.
【答案】(1)见解析;(2)见解析
【解析】(1)作图如图所示,
(2)证明:∵平分,
∴,
又∵,,
∴,
∴.
【点评】此题考查了基本作图--角平分线的画法,以及三角形全等的判定及性质.解题关键是掌握基本作图.
针对练习8
1.如图,在中,,观察图中尺规作图的痕迹,则的度数为( )
A. B. C. D.
【答案】B
【解析】∵在中,,
∴,
∴∠ACD=180°-∠ACB=180°-50°=130°,
由作图痕迹可知CE为∠ACD的平分线,
∴,
故选:B.
2.如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=( )
A.2 B.3 C.4 D.5
【答案】B
【解析】
由作图痕迹可知AD为∠BAC的角平分线,
而AB=AC,
由等腰三角形的三线合一知D为BC重点,
BD=3,
故选B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上期末大串讲+练专题复习
专题五 《全等三角形》考点知识梳理专题训练
知识点归纳
知识点 1: 全等图形
全等形:能够完全重合的两个图形叫做全等形。
(一)全等形的形状相同,大小相等,与图形所在的位置无关。
(二)两个全等形的面积一定相等,但面积相等的两个图形不一定是全等形。
(三)一个图形经过平移、翻折、旋转后,形状、大小都没有改变,只是位置发生了变化,即平移、翻折、旋转前后的图形全等。
知识点2:全等多边形
(1)定义:能够完全重合的两个多边形叫做全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
(2)性质:全等多边形的对应边相等,对应角相等.
(3)判定:边、角分别对应相等的两个多边形全等.
知识点3: 全等三角形
(一)全等三角形:能够完全重合的两个三角形叫做全等三角形。
(二)全等三角形中的对应元素
1、概念:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应顶点:点A与点D,点B与点E,点C与点F。对应边:AB与DE,AC与DF,BC与EF。对应角:∠A与∠D,∠B与∠E,∠C与∠F。
2、对应元素的确定方法
(1)字母顺序确定法∶根据书写规范,按照对应顶点确定对应边、对应角。
(2)图形位置确定法
①公共边一定是对应边;
②公共角一定是对应角;
③对顶角一定是对应角;
(3)图形大小确定法∶两个全等三角形的最大的边(角)是对应边(角),最小的边(角)是对应边(角)。
(三)全等三角形的表示:全等用符号“≌”表示,读作“全等于”。如三角形△ABC和△DEF全等,记作△ABC≌△DEF。记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
知识点4 :全等三角形的性质
(一)全等三角形的对应边相等,全等三角形的对应角相等。
(二)全等三角形对应边上的高、中线分别相等,对应角的平分线相等,面积相等,周长相等。
∵△ABC≌△DEF∴AB=DE,AC=DF,BC=EF(全等三角形的对应边相等)。∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)。
知识点 5 判定全等三角形(边边边)
1、三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
知识点6 判定全等三角形(边角边)
1、用直尺和圆规作一个角等于已知角(已知角∠AOB,求作∠AOB=∠A'O'B')
①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D。
②画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C'。
③以点C'为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D';
④过点D'画射线O'B',则∠A'O'B'=∠AOB。
2、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)。
知识点7 判定全等三角形(角边角)
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
知识点8 判定全等三角形(角角边)
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成"角角边"或"AAS")。
知识点9 判定全等三角形(直角边、斜边)
斜边和一条直角边分别相等的两个直角三角形全等(简写成"斜边、直角边"或"HL")。
注意:用“HL”证明两个直角三角形全等,书写时两个三角形符号前面要加上“Rt”。
知识点10 角的平分线的性质
(一)作已知角的平分线(已知:∠AOB。求作:∠AOB的平分线)
1、以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N。
2、分别以M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C。
3、画射线OC,射线OC即为所求。
(二)角的平分线的性质:角的平分线上的点到角的两边的距离相等。
几何表示:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E。∴PD=PE。
知识点11 角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上。
几何表示:
∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,
∴点P在∠AOB的平分线OC上。
重要拓展:
1、三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等。反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点。
2、三角形的角平分线与三角形一边交于一点,这条角平分线把三角形分成两个小三角形,它们的面积比等于另外两边的长度的比。
∵AD是∠BAC的角平分线;∴DF=DE;∵;;∴ = ;
高频考点:
【考点1】全等图形.
【例1-1】下列4个图形中,属于全等的2个图形是_________.(填序号)
【例1-2】下列四个选项图中,与题图中的图案完全一致的是( )
A. B. C. D.
针对练习1
1.下列各组中的两个图形属于全等图形的是( )
B.
C. D.
2.下列说法正确的是( )
A.两个形状相同的图形称为全等图形
B.两个圆是全等图形
C.全等图形的形状、大小都相同
D.面积相等的两个三角形是全等图形
3 .如图,四边形ABCD≌四边形A'B'C'D',则∠A的度数是 °.
【考点2】全等三角形的性质.
【例2-1】下列说法中,正确的有( )
①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等,面积相等 ④若,则,
A.1个 B.2个 C.3个 D.4个
【例2-2】如图,△ABC≌△DEC,点E在AB上,AC与DE相交于点F,∠BCE=40°.则∠AED的度数为( )
A.40° B.50° C.60° D.70°
【例2-3】如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为 .
针对练习2
1 .若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
2 .如图,图形的各个顶点都在3×3正方形网格的格点上,则∠1+∠2=( )
A.60° B.72° C.45° D.90°
3.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为( )
A.10 B.12 C.14 D.16
【考点3】全等三角形的判定
【例3-1】如图,点在一条直线上,,求证:.
【例3-2】如图,在中,D是延长线上一点,满足,过点C作,且,连接并延长,分别交,于点F,G.
(1)求证:;
(2)若,,求的长度.
【例3-3】如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
【例3-4】如图,∠A=∠D=90°,添加下列条件中的一个后,能判定△ABC与△DCB全等的有( )
①∠ABC=∠DCB;
②∠ACB=∠DBC;
③AB=DC;
④AC=DB.
A.1个 B.2个 C.3个 D.4个
针对练习3
1.如图,已知点是线段上一点,,.
(1)求证:;
(2)求证:.
2 .如图,,,连接交于点O,点E,F在线段上,且.求证:.
3 .已知:如图,、是的高,且.求证:.
4.如图,,和是对应角.在中,是最长边.在中,是最长边,,,.
(1)写出其他对应边及对应角;
(2)求线段及线段的长度.
【考点4】全等三角形的判定与性质
【例4-1】如图,AB=AC,AD=AE,∠BAC=∠DAE,点B,D,E在同一直线上,若∠1=25°,∠2=35°,则∠3的度数是( )
A.50° B.55° C.60° D.70°
【例4-2】如图,在平面直角坐标系中,△ABC的顶点A(3,0),B(0,﹣1),点C在第四象限,且AB=BC,∠ABC=90°,则点C的坐标是( )
A.(﹣4,1) B.(1,﹣4) C.(﹣1,4) D.(4,﹣1)
【例4-3】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
针对练习4
1.如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O.
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠A=51°,求∠BOF的度数.
2 .如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
3 .如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
如图,CD=BE,∠C=∠B,∠1=∠2.
(1)求证:△ABE≌△ACD.
(2)若ME=5,求DN的长度.
【考点5】全等三角形的应用
【例5-1】如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
【例5-2】如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5米,则槽宽为( )
A.3 B.4 C.5 D.6
【例5-3】如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
针对练习5
1 .如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
2 如图,某人将一块三角形玻璃打碎成两块,带 ② 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
3 .王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
【考点6】角平分线的性质
【例6-1】如图,已知,射线平分,过点E作于点H,作于点F,并延长交于点G,连接.若,则的长为 .
【例6-2】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长( )
A.3cm B.4cm C.5cm D.6cm
【例6-3】如图,中,,的平分线交于点D,若,则点D到的距离是 cm.
针对练习6
如图,已知△ABC的周长是18,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则△ABC的面积是( )
A.6 B.9 C.18 D.36
2 .如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.5:3:2 C.2:3:4 D.3:4:5
3.如图,AD∥BC,∠D=90°,∠CPB=30°,∠DAB的角平分线与∠CBA的角平分线相交于点P,且D,P,C在同一条直线上.
(1)求∠PAD的度数;
(2)求证:P是线段CD的中点.
【考点7】角平分线的判定
【例7-1】如图,A、B两点分别在射线OM,ON上,点C在∠MON的内部,且AC=BC,CD⊥OM,CE⊥ON,垂足分别为D,E,且AD=BE.
(1)求证:OC平分∠MON;
(2)若AD=3,BO=4,求AO的长.
【例7-2】如图,已知垂足为,垂足为,,.
(1)求证:平分;
(2)丁丁同学观察图形后得出结论:,请你帮他写出证明过程.
【例7-3】已知:如图,在中,,D是上一点,于E,且.
(1)求证:平分;
(2)若,求的度数.
针对练习7
1 .如图,在中,的平分线与的外角平分线交于点,于点,于点.
(1)若,求点到直线的距离;
(2)求证:点在的平分线上.
2.求证:三角形两外角的平分线的交点到三角形三边(或所在的直线)距离相等.
要求:画图,写出已知,求证,然后写出证明过程.
【考点8】尺规作图:(1)作一个角等于已知角(2)作已知角的平分线
【例8-1】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.
已知:如图,直线和直线外一点.
求作:直线,使直线直线.
作法:如图,
①在直线上任取一点,作射线;
②以为圆心,为半径作弧,交直线于点,连接;
③以为圆心,长为半径作弧,交射线于点;分别以为圆心,大于长为半径作弧,在的右侧两弧交于点;
④作直线;
所以直线就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知平分,
.
又,
.(_______________________________)(填依据1).
,
.
,∴直线直线.(______________________)(填依据2).
【例8-2】如图,已知锐角,.
(1)尺规作图:求作的角平分线;(保留作图痕迹,不写作法)
(2)点在边上且,请连接,求证:.
针对练习8
1.如图,在中,,观察图中尺规作图的痕迹,则的度数为( )
A. B. C. D.
2.如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=( )
A.2 B.3 C.4 D.5
八年级数学上期末大串讲+练专题复习
专题五 《全等三角形》考点知识梳理专题训练
知识点归纳
知识点 1: 全等图形
全等形:能够完全重合的两个图形叫做全等形。
(一)全等形的形状相同,大小相等,与图形所在的位置无关。
(二)两个全等形的面积一定相等,但面积相等的两个图形不一定是全等形。
(三)一个图形经过平移、翻折、旋转后,形状、大小都没有改变,只是位置发生了变化,即平移、翻折、旋转前后的图形全等。
知识点2:全等多边形
(1)定义:能够完全重合的两个多边形叫做全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
(2)性质:全等多边形的对应边相等,对应角相等.
(3)判定:边、角分别对应相等的两个多边形全等.
知识点3: 全等三角形
(一)全等三角形:能够完全重合的两个三角形叫做全等三角形。
(二)全等三角形中的对应元素
1、概念:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应顶点:点A与点D,点B与点E,点C与点F。对应边:AB与DE,AC与DF,BC与EF。对应角:∠A与∠D,∠B与∠E,∠C与∠F。
2、对应元素的确定方法
(1)字母顺序确定法∶根据书写规范,按照对应顶点确定对应边、对应角。
(2)图形位置确定法
①公共边一定是对应边;
②公共角一定是对应角;
③对顶角一定是对应角;
(3)图形大小确定法∶两个全等三角形的最大的边(角)是对应边(角),最小的边(角)是对应边(角)。
(三)全等三角形的表示:全等用符号“≌”表示,读作“全等于”。如三角形△ABC和△DEF全等,记作△ABC≌△DEF。记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
知识点4 :全等三角形的性质
(一)全等三角形的对应边相等,全等三角形的对应角相等。
(二)全等三角形对应边上的高、中线分别相等,对应角的平分线相等,面积相等,周长相等。
∵△ABC≌△DEF∴AB=DE,AC=DF,BC=EF(全等三角形的对应边相等)。∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)。
知识点 5 判定全等三角形(边边边)
1、三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
知识点6 判定全等三角形(边角边)
1、用直尺和圆规作一个角等于已知角(已知角∠AOB,求作∠AOB=∠A'O'B')
①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D。
②画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C'。
③以点C'为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D';
④过点D'画射线O'B',则∠A'O'B'=∠AOB。
2、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)。
知识点7 判定全等三角形(角边角)
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
知识点8 判定全等三角形(角角边)
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成"角角边"或"AAS")。
知识点9 判定全等三角形(直角边、斜边)
斜边和一条直角边分别相等的两个直角三角形全等(简写成"斜边、直角边"或"HL")。
注意:用“HL”证明两个直角三角形全等,书写时两个三角形符号前面要加上“Rt”。
知识点10 角的平分线的性质
(一)作已知角的平分线(已知:∠AOB。求作:∠AOB的平分线)
1、以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N。
2、分别以M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C。
3、画射线OC,射线OC即为所求。
(二)角的平分线的性质:角的平分线上的点到角的两边的距离相等。
几何表示:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E。∴PD=PE。
知识点11 角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上。
几何表示:
∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,
∴点P在∠AOB的平分线OC上。
重要拓展:
1、三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等。反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点。
2、三角形的角平分线与三角形一边交于一点,这条角平分线把三角形分成两个小三角形,它们的面积比等于另外两边的长度的比。
∵AD是∠BAC的角平分线;∴DF=DE;∵;;∴ = ;
高频考点:
【考点1】全等图形.
【考点1】全等图形.
【例1-1】下列4个图形中,属于全等的2个图形是_________.(填序号)
【答案】①③
【分析】先求出的度数,然后分析求解即可.
【详解】解:在③中,,
∴与①中的相等,并且两夹边对应相等,
∴属于全等的2个图形是①③
故答案为①③.
【点评】本题考查了三角形全等的条件,熟悉全等三角形的判定定理是解题的关键.
【例1-2】下列四个选项图中,与题图中的图案完全一致的是( )
A. B. C. D.
【答案】A
【分析】根据全等形是能够完全重合的两个图形进行分析判断.
【详解】解:将原图绕其中心顺时针旋转144度后,可以和A中的图形重合;
原图通过旋转变换不能得到与B、C、D中的图形重合,
故选:A.
【点睛】本题考查的是全等形的识别,通过旋转找出原图与选项中的图形重合是解题的关键。
针对练习1
1.下列各组中的两个图形属于全等图形的是( )
B.
C. D.
【答案】B
【分析】根据全等图形的定义,逐一判断选项,即可.
【详解】解:A、两个图形不能完全重合,不属于全等图形,故此选项不符合题意;
B、两个图形能完全重合,属于全等图形,故此选项符合题意;
C、两个图形不能完全重合,不属于全等图形,故此选项不符合题意;
D、两个图形不能完全重合,不属于全等图形,故此选项不符合题意.
故选:B.
【点评】本题主要考查全等图形的定义,熟练掌握“能完全重合的两个图形,是全等图形”是解题的关键.
2.下列说法正确的是( )
A.两个形状相同的图形称为全等图形
B.两个圆是全等图形
C.全等图形的形状、大小都相同
D.面积相等的两个三角形是全等图形
【答案】C
【解答】解:A、两个形状相同、大小相同的图形是全等图形,故原命题错误,不符合题意;
B、两个圆的形状相同但大小不相同,不是全等图形,故原命题错误,不符合题意;
C、全等图形的形状、大小都相同,正确,符合题意;
D、面积相等的两个三角形不一定是全等图形,故原命题错误,不符合题意.
故选:C.
3 .如图,四边形ABCD≌四边形A'B'C'D',则∠A的度数是 °.
【答案】95.
【分析】利用相似多边形对应角相等即可求解.
【解答】解:∵四边形ABCD∽四边形A′B′C′D′,
∴∠D=∠D′=130°,
∴∠C′=360°﹣130°﹣60°﹣75°=95°
∴∠α=∠C′=95°,
故答案为:95.
【考点2】全等三角形的性质.
【例2-1】下列说法中,正确的有( )
①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等,面积相等 ④若,则,
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】根据全等的定义和性质判断即可.
【详解】①形状大小都相同的两个图形是全等形,故①错误;
②面积相等的两个图形不一定是全等形,故②错误;
③全等三角形的周长相等,面积相等,是对的,故③正确;
④若,则,,故④错误;
故正确的有1个.
故选:A
【点睛】此题考查全等三角形的定义和性质,解题关键是掌握全等三角形的定义.
【例2-2】如图,△ABC≌△DEC,点E在AB上,AC与DE相交于点F,∠BCE=40°.则∠AED的度数为( )
A.40° B.50° C.60° D.70°
【答案】A
【分析】由△ABC≌△DEC,得∠DEC=∠B=73°,BC=EC,再求出∠CEB=∠B,最后根据平角的性质即可得答案.
【解答】解:∵△ABC≌△DEC,
∴BC=EC,∠CED=∠B,
∴∠CEB=∠B,
∵∠BCE=40°,
∴∠CEB=∠B==70°,
∴∠AED=180°﹣∠DEC﹣∠CEB=180°﹣70°﹣70°=40°,
故选:A.
【例2-3】如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为 .
【答案】 或 或(-1,3)
【解析】【解答】解:因为 与 的一条边 重合
当点D在 的下方时,满足条件的坐标有 和 ;
当点D在 的上方时,满足条件的坐标是 .
故满足条件的为 或 或(-1,3)
针对练习2
1 .若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
【答案】A
【分析】直接利用全等三角形的性质得出对应边相等进而得出答案.
【解答】解:∵△ABC≌△DEF,
∴BC=EF=30,
故选:A.
2 .如图,图形的各个顶点都在3×3正方形网格的格点上,则∠1+∠2=( )
A.60° B.72° C.45° D.90°
【答案】C
【解答】解:如图所示,∵AB=AD=1,BC=DE=2,∠ABC=∠ADE=90°,
∴△ABC≌△ADE(SAS),
∴∠AED=∠1,
∴∠1+∠2=∠2+∠AED=∠BEF,
∵EF=BF=1,∠BFE=90°,
∴∠BEF=45°,
∴∠1+∠2=∠BEF=45°.
故选:C.
3.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为( )
A.10 B.12 C.14 D.16
【答案】C
【分析】由全等三角形的性质得出△DOC的周长为10,进而得出△DBC的周长=△DOC的周长+BC即可.
【解答】解:∵△AOB≌△DOC,△AOB的周长为10,
∴△DOC的周长为10,OB=OC,
∴△DBC的周长=DO+OB+DC+BC
=DO+OC+DC+BC
=△DOC的周长+BC
=10+4
=14.
故选:C.
【考点3】全等三角形的判定
【例3-1】如图,点在一条直线上,,求证:.
【答案】见解析
【分析】根据题意,运用“边边边”的方法证明三角形全等.
【详解】证明:∵,
∴,即,
在和中
∴.
【点睛】本题主要考查三角形全等的判定,掌握全等三角形的判定方法解题的关键.
【例3-2】如图,在中,D是延长线上一点,满足,过点C作,且,连接并延长,分别交,于点F,G.
(1)求证:;
(2)若,,求的长度.
【答案】(1)见解析
(2)4
【分析】(1)根据证明即可;
(2)根据全等三角形的性质解答即可.
【详解】(1)∵,
∴,
在与中,
,
∴;
(2)∵,
∴,
∵,
∴,
∵,
∴
∴.
【点睛】此题考查全等三角形的判定和性质,关键是掌握全等三角形的判定和性质.
【例3-3】如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
【答案】D
【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出即可.
【解答】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:D.
【例3-4】如图,∠A=∠D=90°,添加下列条件中的一个后,能判定△ABC与△DCB全等的有( )
①∠ABC=∠DCB;
②∠ACB=∠DBC;
③AB=DC;
④AC=DB.
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】根据题意和图形,可以得到∠A=∠D=90°,BC=CB,然后根据各个选项中的条件,结合全等三角形的判定定理即可求解.
【解答】解:①添加条件∠ABC=∠DCB,又∠A=∠D=90°,BC=CB,由AAS能判定△ABC与△DCB全等,故①符合题意;
②添加条件∠ACB=∠DBC,又∠A=∠D=90°,BC=CB,由AAS能判定△ABC与△DCB全等,故②符合题意;
③添加条件AB=DC,又∠A=∠D=90°,BC=CB,由HL能判定△ABC与△DCB全等,故③符合题意;
④添加条件AC=DB,又∠A=∠D=90°,BC=CB,由HL能判定△ABC与△DCB全等,故④符合题意.
故选:D.
针对练习3
1.如图,已知点是线段上一点,,.
(1)求证:;
(2)求证:.
【答案】(1)见解析
(2)见解析
【分析】(1)由得,即,从而即可证得;
(2)由可得,,即可得到,从而即可得证.
【详解】(1)证明:,
,
,
在和中,
,
;
(2)解:,
,,
,
.
【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
2 .如图,,,连接交于点O,点E,F在线段上,且.求证:.
【分析】利用已知条件证明,推出,由,得到,即.
【详解】证明:∵,
∴,
在和中,,
∴,
∴,
∵,
∴,
即.
【点睛】此题考查全等三角形的性质与判定,解题的关键是证明.
3 .已知:如图,、是的高,且.求证:.
【分析】根据、是的高得到直角,再证明≌即可得到结论.
【详解】证明:、是的高,
,,
,
在和中,
,
≌,
.
【点睛】本题考查全等三角形的性质和判定,利用证明直角三角形全等是本题关键.
4.如图,,和是对应角.在中,是最长边.在中,是最长边,,,.
(1)写出其他对应边及对应角;
(2)求线段及线段的长度.
【答案】(1)对应边:和,和;对应角:和,和.
(2),
【分析】(1)由和是对应角可知F和M点是对应点,结合最长边对应关系可知和相对应,再由对应边所对的角也是对应关系可知和是对应角,据此进行逐一判断即可;
(2)由(1)所得对应关系可知,,由,可得.
【详解】(1)解:对应边:和,和;对应角:和,和.
(2)∵,
∴,,
∵,
∴.
【点睛】本题考查了全等三角形的性质,熟练掌握全等三角形的对应边相等,对应角相等是解题的关键.
【考点4】全等三角形的判定与性质
【例4-1】如图,AB=AC,AD=AE,∠BAC=∠DAE,点B,D,E在同一直线上,若∠1=25°,∠2=35°,则∠3的度数是( )
A.50° B.55° C.60° D.70°
【答案】C
【分析】先证明△BAD≌△CAE(SAS),根据全等三角形的性质可得∠1=∠ABD,再根据外角的性质,即可求出∠3.
【解答】解:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠1=∠ABD,
∵∠1=25°,∠2=35°,
∴∠3=∠2+∠ABD=60°,
故选:C.
【例4-2】如图,在平面直角坐标系中,△ABC的顶点A(3,0),B(0,﹣1),点C在第四象限,且AB=BC,∠ABC=90°,则点C的坐标是( )
A.(﹣4,1) B.(1,﹣4) C.(﹣1,4) D.(4,﹣1)
【答案】B
【分析】过点C作CE⊥y轴于E,根据AAS证明△AOB与△BEC全等,进而解答即可.
【解答】解:过点C作CE⊥y轴于E,
∵∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠AOB=90°,
∴∠ABO+∠BAO=90°,
∴∠BAO=∠CBE,
在△AOB与△BEC中,
,
∴△AOB≌△BEC(AAS),
∴OB=EC=1,BE=OA=3,
∴OE=OB+BE=1+3=4,
∴点C坐标(1,﹣4),
故选:B.
【例4-3】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;
(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.
【解答】(1)证明:∵∠BAC=∠FAG,
∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,
∴∠BAD=∠CAG,
在△ABF和△ACG中,
,
∴△ABF≌△ACG(ASA);
(2)证明:∵△ABF≌△ACG,
∴AF=AG,BF=CG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵∠BAD=∠CAG,
∴∠CAD=∠CAG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS).
∴EF=EG,
∴BE=BF+FE=CG+EG.
针对练习4
1.如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O.
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠A=51°,求∠BOF的度数.
【答案】(1)证明见解答;
(2)78°.
【分析】(1)根据HL证明两个三角形全等;
(2)根据三角形全等的性质和三角形外角的性质可得结论.
【解答】(1)证明:∵AE=DB,
∴AE+EB=DB+EB,即AB=DE,
在Rt△ACB和Rt△DFE中,
,
∴Rt△ABC≌Rt△DEF(HL);
(2)解:∵∠C=90°,∠A=51°,
∴∠ABC=∠C﹣∠A=90°﹣51°=39°,
由(1)知Rt△ABC≌Rt△DEF,
∴∠ABC=∠DEF.
∴∠DEF=39°,
∴∠BOF=∠ABC+∠BEF=39°+39°=78°.
2 .如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
【答案】见试题解答内容
【分析】(1)由ASA证明△ABD≌△COD即可;
(2)理由全等三角形的性质即可解决问题;
【解答】(1)证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠BAD+∠B=∠FCD+∠B=90°,
∴∠BAD=∠FCD,
在△ABD和CFD中,
,
∴△ABD≌△CFD(ASA),
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
3 .如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
【答案】见试题解答内容
【分析】(1)根据题意和题目中的条件可以找出△ABC≌△ADE的条件;
(2)根据(1)中的结论和等腰直角三角形的定义可以得到∠FAE的度数;
(3)根据题意和三角形全等的知识,作出合适的辅助线即可证明结论成立.
【解答】证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS);
(2)∵∠CAE=90°,AC=AE,
∴∠E=45°,
由(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°;
(3)延长BF到G,使得FG=FB,
∵AF⊥BG,
∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,
,
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA,
∵∠GCA=∠DCA=45°,
在△CGA和△CDA中,
,
∴△CGA≌△CDA(AAS),
∴CG=CD,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
如图,CD=BE,∠C=∠B,∠1=∠2.
(1)求证:△ABE≌△ACD.
(2)若ME=5,求DN的长度.
【答案】(1)证明见解答;
(2)DN=5.
【分析】(1)根据已知条件利用AAS证明△ABE≌△ACD;
(2)先根据△ABE≌△ACD得出AB=AC,∠E=∠D,再利用ASA证明△ABM≌△ACD,然后得出AM=AN,再证明△ADN≌△AEM,从而得出DN=ME.
【解答】(1)证明∵∠1=∠2,
∴∠BAE=∠CAD,
∵CD=BE,∠C=∠B,
∴△ABE≌△ACD(AAS);
(2)解:∵△ABE≌△ACD,
∴AB=AC,∠E=∠D,
∵∠C=∠B,∠1=∠2,
∴△ABM≌△ACD(ASA),
∴AM=AN,
∵∠DAN=∠EAM,∠E=∠D,
∴△ADN≌△AEM(AAS),
∴DN=ME=5.
【考点5】全等三角形的应用
【例5-1】如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
【分析】先根据BC=EF,AC=DF判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质可知,∠1=∠4,再由直角三角形的两锐角互余即可解答.
【解答】解:∵滑梯、墙、地面正好构成直角三角形,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF(HL),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠ACB+∠DEF=90°.
故选:C.
【例5-2】如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5米,则槽宽为( )
A.3 B.4 C.5 D.6
【分析】连接AB,如图,利用“SAS”证明△OAB≌△OA′B′,从而得到A′B′=AB=5m.
【解答】解:连接AB,如图,
在△OAB和△OA′B′中
∴△OAB≌△OA′B′(SAS),
∴A′B′=AB=5(m).
答:槽宽为5m.
故选:C.
【例5-3】如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
【分析】利用全等三角形的判定方法进行分析即可.
【解答】解:在△ABC和△MBC中,
∴△MBC≌△ABC(ASA),
故选:D.
针对练习5
1 .如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
【分析】根据全等三角形的判定进行判断,注意看题目中提供了哪些证明全等的要素,要根据已知选择判断方法.
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC=90°,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:D.
2 如图,某人将一块三角形玻璃打碎成两块,带 ② 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
【分析】已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.
【解答】解:第①块只保留了原三角形的一个角和部分边,根据这两块中的任一块不能配一块与原来完全一样的;
第②块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带②去.
故答案为:②,ASA.
3 .王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
【分析】根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
【考点6】角平分线的性质
【例6-1】如图,已知,射线平分,过点E作于点H,作于点F,并延长交于点G,连接.若,则的长为 .
【答案】2
【分析】先根据平行线的性质可得,再根据角平分线的定义和“等角的余角相等”可得,再由,可得,由角平分线的性质可得,即可求出的长.
【详解】,
,
即.
,
,
.
∵平分,
,
,
∴平分.
,
.
,
,
∴.
故答案为:2
【点睛】本题主要考查了平行线的性质,角平分线的性质,“等角对等边”.熟练掌握以上知识,且证明平分是解题的关键.
【例6-2】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长( )
A.3cm B.4cm C.5cm D.6cm
【答案】A
【分析】根据角平分线的性质得到DE=DF,根据三角形的面积公式计算即可.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=×AB×DE+×AC×DF=30(cm2),即×13×DE+×7×DF=30,
解得DE=DF=3cm,
故选:A.
【例6-3】如图,中,,的平分线交于点D,若,则点D到的距离是 cm.
【答案】3
【分析】过D作于E.根据角平分线性质求解即可.
【详解】解:过D作于E.如图,
∵是的平分线,,,
∴.
∵,
∴.
故答案为:3.
【点睛】本题主要考查角平分线的性质;作出辅助线是正确解答本题的关键.
针对练习6
如图,已知△ABC的周长是18,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则△ABC的面积是( )
A.6 B.9 C.18 D.36
【答案】C
【分析】由角平分线的性质得到OM=OD=ON,由△ABC的面积=△AOB的面积+△OBC的面积+△OAC的面积,得到△ABC的面积=(AB+BC+AC) OD,由△ABC的周长=18,OD=2,即可求出△ABC的面积=×18×2=18.
【解答】解:过O作OM⊥AB于M,ON⊥AC于N,
∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,
∴OM=OD,ON=OD,
∵△ABC的面积=△AOB的面积+△OBC的面积+△OAC的面积,
∴△ABC的面积=AB OM+BC OD+AC ON=(AB+BC+AC) OD,
∵△ABC的周长=18,OD=2,
∴△ABC的面积=×18×2=18.
故选:C.
2 .如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.5:3:2 C.2:3:4 D.3:4:5
【答案】A
【分析】过点O作OD⊥AB于点D,OE⊥BC于点E,OF⊥AC于点F,根据角平分线的性质定理可知OD=OE=OF.再由三角形的面积公式计算,作比即可.
【解答】解:如图,过点O作OD⊥AB于点D,OE⊥BC于点E,OF⊥AC于点F,
∵点O是△ABC三条角平分线的交点,
∴OD=OE=OF,
∵,
,
,
∴S△OAB:S△OBC:S△OAC=8OD:6OE:4OF=4:3:2.
故选:A.
3.如图,AD∥BC,∠D=90°,∠CPB=30°,∠DAB的角平分线与∠CBA的角平分线相交于点P,且D,P,C在同一条直线上.
(1)求∠PAD的度数;
(2)求证:P是线段CD的中点.
优网版权所有
【答案】(1)30°;
(2)见解答.
【分析】(1)根据平行线的性质得到∠C=180°﹣∠D=90°,∠DAB+∠ABC=180°,再计算出∠PBC=60°,则利用角平分线的定义得到∠ABC=120°,所以∠DAB=60°,然后利用角平分线的定义得到∠PAD的度数;
(2)过P点作PE⊥AB于E点,如图,根据角平分线的性质得到PE=PD,PE=PC,从而得到PD=PC.
【解答】(1)解:∵AD∥BC,
∴∠C=180°﹣∠D=180°﹣90°=90°,
∵∠CPB=30°,
∴∠PBC=90°﹣∠B=60°,
∵PB平分∠ABC,
∴∠ABC=2∠PBC=120°,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠DAB=180°﹣120°=60°,
∵AP平分∠DAB,
∴∠PAD=∠DAB=30°;
(2)证明:过P点作PE⊥AB于E点,如图,
∵AP平分∠DAB,PD⊥AD,PE⊥AB,
∴PE=PD,
∵BP平分∠ABC,PC⊥BC,PE⊥AB,
∴PE=PC,
∴PD=PC,
∴P是线段CD的中点.
【考点7】角平分线的判定
【例7-1】如图,A、B两点分别在射线OM,ON上,点C在∠MON的内部,且AC=BC,CD⊥OM,CE⊥ON,垂足分别为D,E,且AD=BE.
(1)求证:OC平分∠MON;
(2)若AD=3,BO=4,求AO的长.
【分析】(1)根据全等三角形的判定定理推出Rt△ADC≌Rt△BEC,根据全等三角形的性质得出CD=CE,再得出答案即可;
(2)根据全等三角形的性质得出AD=BE=3,根据全等三角形的判定定理推出Rt△ODC≌Rt△OEC,根据全等三角形的性质得出OD=OB,再求出答案即可.
【解答】(1)证明:∵CD⊥OM,CE⊥ON,
∴∠ADC=∠CEB=90°,
在Rt△ADC和Rt△BEC中,
,
∴Rt△ADC≌Rt△BEC(HL),
∴CD=CE,
∵CD⊥OM,CE⊥ON,
∴OC平分∠MON;
(2)解:∵Rt△ADC≌Rt△BEC,AD=3,
∴BE=AD=3,
∵BO=4,
∴OE=OB+BE=4+3=7,
∵CD⊥OM,CE⊥ON,
∴∠CDO=∠CEO=90°,
在Rt△DOC和Rt△EOC中,
,
∴Rt△DOC≌Rt△EOC(HL),
∴OD=OE=7,
∵AD=3,
∴OA=OD+AD=7+3=10.
【例7-2】如图,已知垂足为,垂足为,,.
(1)求证:平分;
(2)丁丁同学观察图形后得出结论:,请你帮他写出证明过程.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)首先用判断出,根据全等三角形的对应边相等得,进而根据到角两边距离相等的点在这个角的角平分线上可得平分;
(2)首先用判断出,根据全等三角形的对应边相等得,结合,根据线段的和差即可得出结论.
【详解】(1)证明:,,
,
在和中,
,
,
,
,,
,
平分;
(2)解:,
在和中
,
,
,
,
.
【点睛】本题考查全等三角形的判定与性质,角平分线的判定定理,能正确根据全等三角形的判定和性质定理进行推理是解此题的关键.
【例7-3】已知:如图,在中,,D是上一点,于E,且.
(1)求证:平分;
(2)若,求的度数.
【答案】(1)见解析
(2)
【分析】(1)根据已知条件结合角平分线判定定理即可证明.
(2)根据直角三角形的两个锐角互余求得度数.
【详解】(1)证明:,,,
点D在的平分线上,
平分.
(2)解:,,
,
平分,
.
【点睛】本题主要考查了角平分线的判定与性质运用,和直角三角形性质的运用,熟练掌握角平分线的判定定理是解答的关键.
针对练习7
1 .如图,在中,的平分线与的外角平分线交于点,于点,于点.
(1)若,求点到直线的距离;
(2)求证:点在的平分线上.
【答案】(1)8cm
(2)见解析
【分析】(1)利用角平分线上一点到角两边距离相等即可求解;
(2)利用如果一点到角的两边距离相等,则这个点在角的角平分线上.
【详解】(1)解:作于,如图,
又∵平分,,
∴,
即点到直线的距离为8cm;
(2)证明:∵平分,且于点,,
∴,
又,
∴,
∴点在的平分线上.
【点睛】本题考查角平分线性质定理以及逆定理,熟练掌握角平分性质的逆用是解决本题的关键。
2.求证:三角形两外角的平分线的交点到三角形三边(或所在的直线)距离相等.
要求:画图,写出已知,求证,然后写出证明过程.
【详解】解;已知:如图,的外角平分线与外角平分线相交于点P.
求证:;
证明:如图,过点P作于F,于G,于H,
∵的外角平分线与相交于点P,
∴,,
∴.
即点P到三边、、所在直线的距离相等
∴三角形两外角的平分线的交点到三角形三边(或所在直线)的距离相等.
【考点8】尺规作图:(1)作一个角等于已知角(2)作已知角的平分线
【例8-1】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.
已知:如图,直线和直线外一点.
求作:直线,使直线直线.
作法:如图,
①在直线上任取一点,作射线;
②以为圆心,为半径作弧,交直线于点,连接;
③以为圆心,长为半径作弧,交射线于点;分别以为圆心,大于长为半径作弧,在的右侧两弧交于点;
④作直线;
所以直线就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知平分,
.
又,
.(_______________________________)(填依据1).
,
.
,∴直线直线.(______________________)(填依据2).
【答案】(1)作图见解析;(2)等边对等角;同位角相等,两直线平行
【解析】解:(1)根据题中画图过程可得:
如图,PQ即为所作图形;
(2)由作图可知平分,
.
又,
.(等边对等角).
,
.
,
∴直线直线.(同位角相等,两直线平行).
【点评】本题考查了尺规作图,等腰三角形的性质,平行线的判定,解题的关键是根据题意作图,然后再进行推理论证.
【例8-2】如图,已知锐角,.
(1)尺规作图:求作的角平分线;(保留作图痕迹,不写作法)
(2)点在边上且,请连接,求证:.
【答案】(1)见解析;(2)见解析
【解析】(1)作图如图所示,
(2)证明:∵平分,
∴,
又∵,,
∴,
∴.
【点评】此题考查了基本作图--角平分线的画法,以及三角形全等的判定及性质.解题关键是掌握基本作图.
针对练习8
1.如图,在中,,观察图中尺规作图的痕迹,则的度数为( )
A. B. C. D.
【答案】B
【解析】∵在中,,
∴,
∴∠ACD=180°-∠ACB=180°-50°=130°,
由作图痕迹可知CE为∠ACD的平分线,
∴,
故选:B.
2.如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=( )
A.2 B.3 C.4 D.5
【答案】B
【解析】
由作图痕迹可知AD为∠BAC的角平分线,
而AB=AC,
由等腰三角形的三线合一知D为BC重点,
BD=3,
故选B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
