切线长定理

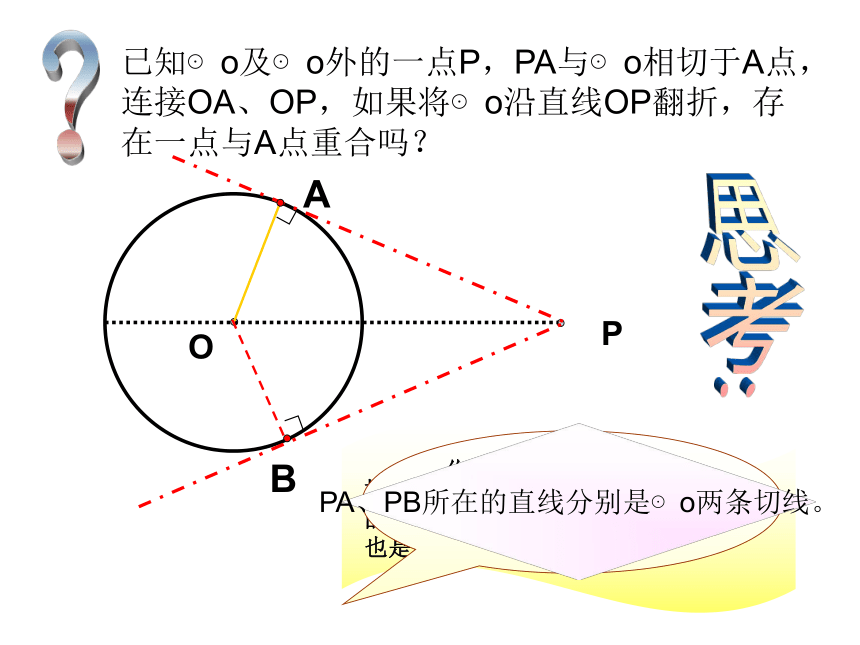
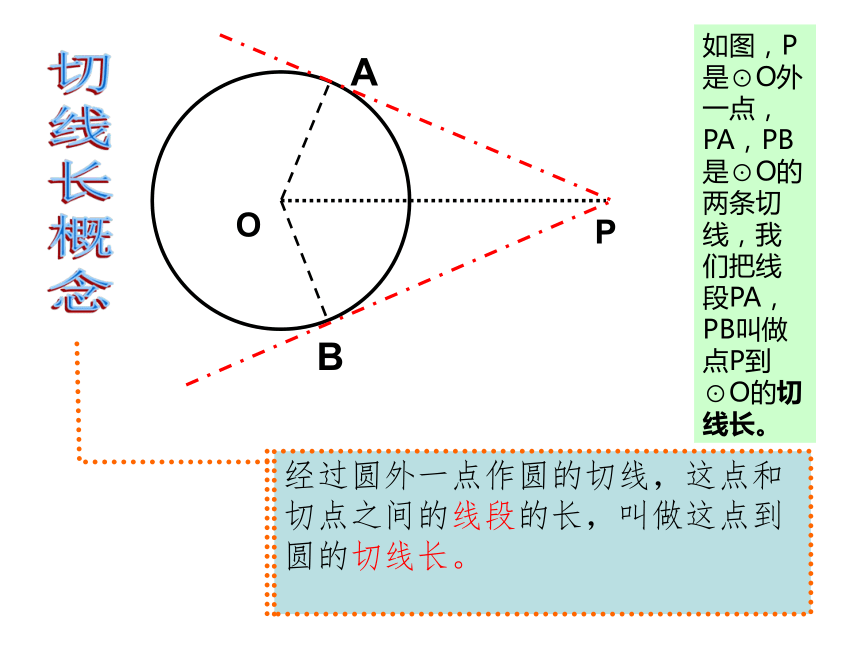
课件12张PPT。宿城区陈集中学 陈加形切线长定理已知⊙o及⊙o外的一点P，PA与⊙o相切于A点，连接OA、OP，如果将⊙o沿直线OP翻折，存在一点与A点重合吗？思考:？OPAB你能发现OA与PA，OB与PB之间的关系吗？PA、PB所在的直线分别是⊙o两条切线。∟∟切线长概念经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长。如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长。OPAB
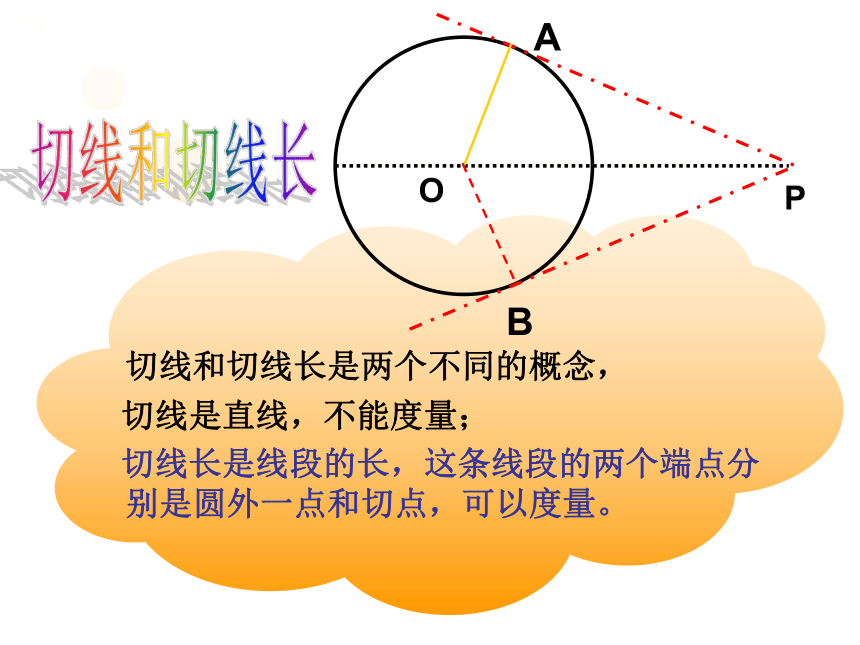
切线和切线长是两个不同的概念，
切线是直线，不能度量；
切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。切线和切线长OPAB∟∟M根据你的直观判断，猜想图中PA是否等于PB？∠1与∠2又有什么关系？大胆猜想:
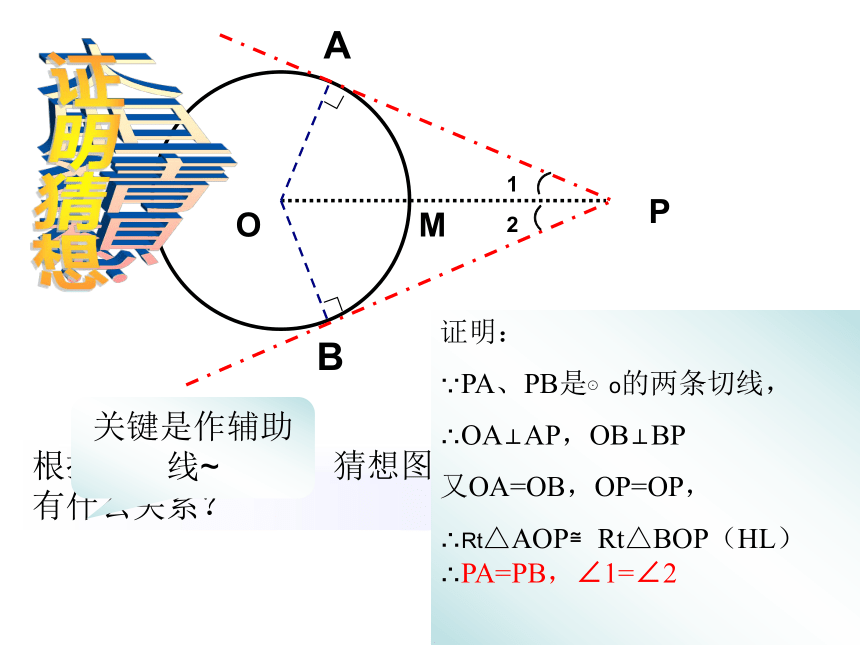
　　⌒⌒12证明：
∵PA、PB是⊙o的两条切线，
∴OA⊥AP，OB⊥BP
又OA=OB，OP=OP，
∴Rt△AOP≌Rt△BOP（HL）∴PA=PB，∠1=∠2
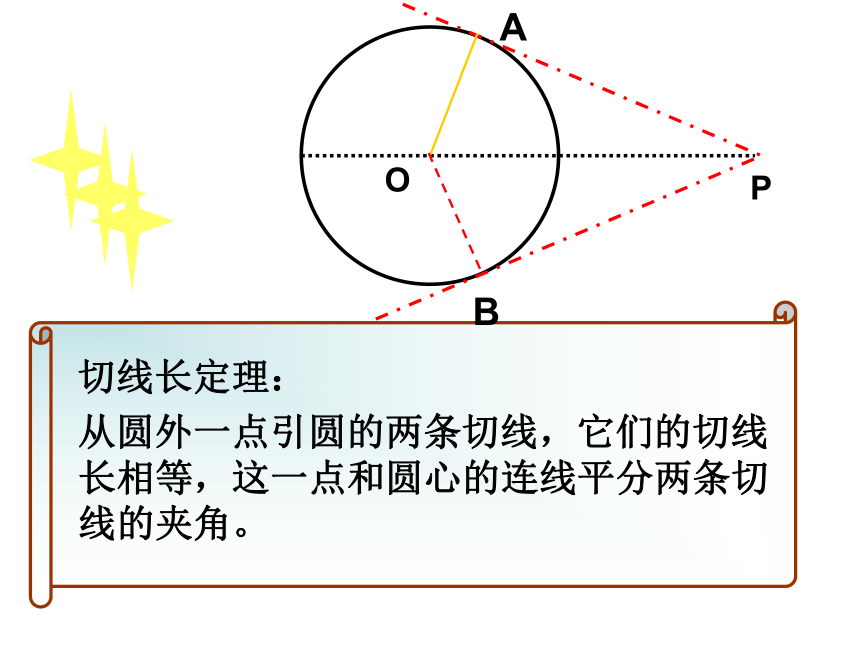
证明猜想关键是作辅助线~ 切线长定理：
从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。已知：⊙O的半径为3厘米，点P和圆心O的距离为6厘米，经过点P和⊙O的两条切线，求这两条切线的夹角及切线长．练习一OFPE⌒12⌒切线长定理的拓展
　　BOPAHDC想一想：根据图形，
你还可以得到什么结论？PABCO如AC为直径，观察OP与BC的位置关系，并给予证明。巩固练习：（1）已知OA=3cm,OP=6cm，则PA=——，∠APB=——3√360°（2）OP交⊙O于M，则——————，ＡＢ与ＯＰ有何关系？ＡＭ＝ＢＭ⌒⌒M已知：如图,PA、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA=12CM，∠P=70
求：△PEF的周长。EAQPFBO小结：（1）切线长定理。（2）连接圆心和切点是我们解决切线长定理相关问题时常用的辅助线。谢谢！