第5单元圆易错精选题(含答案)数学六年级上册人教版
文档属性
| 名称 | 第5单元圆易错精选题(含答案)数学六年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 17:53:25 | ||
图片预览

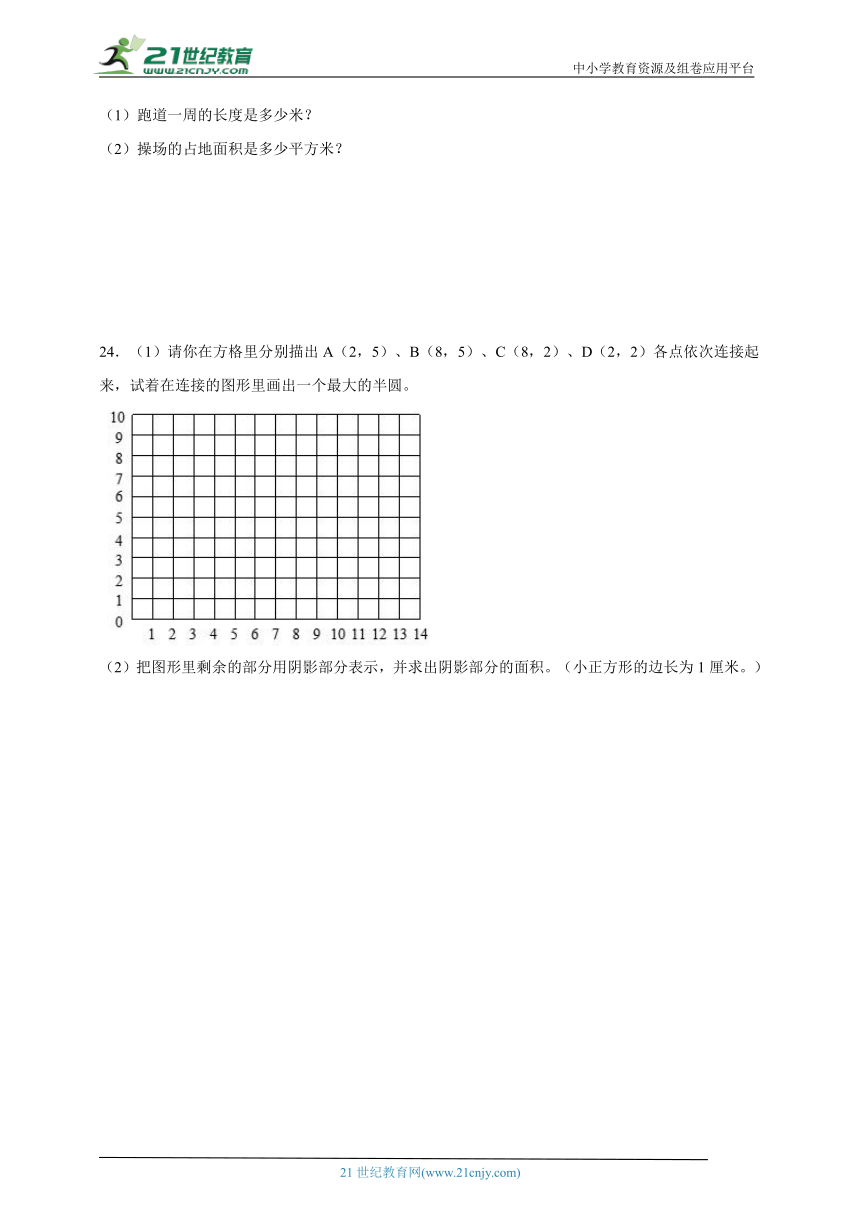
文档简介
中小学教育资源及组卷应用平台
第5单元圆易错精选题-数学六年级上册人教版
一、选择题
1.如图,在正方形里画一个最大的圆,圆的面积与正方形面积的比是( )。
A. B. C. D.
2.关于“圆周率”的认识,你同意的是( )。
A.圆周率是圆的周长
B.圆周率是圆周长和直径的倍数关系
C.圆周率是圆周长和半径的倍数关系
D.圆周率是圆面积和直径的倍数关系
3.圆的半径由3cm增加到4cm,这个圆的面积增加了( )cm2。
A.1 B.7 C.7π D.π
4.下列说法错误的是( )。
①一个真分数的倒数一定比这个真分数大。
②一个数乘分数的积一定比原来的数小。
③一个数除以分数的商一定比原来的数大。
④大牛和小牛的数量比是4∶5,表示大牛比小牛少。
⑤圆周率π就是3.14。
⑥用4个圆心角都是90°的扇形,一定可以拼成一个圆。
A.②③④⑤⑥ B.②③⑤⑥ C.① D.②③⑤
5.一个圆的直径扩大4倍,它的周长扩大( )倍。
A.4 B.16 C.2 D.8
6.小东想在空地上围出一块面积为706.5平方米的圆形土地来种菜他应该用多长的篱笆来围(圆周率取3.14)。( )
A.78.5米 B.87.5米 C.92.4米 D.94.2米
二、填空题
7.两个圆的半径之比为2∶3,它们的周长之比是( ),面积之比是( )。
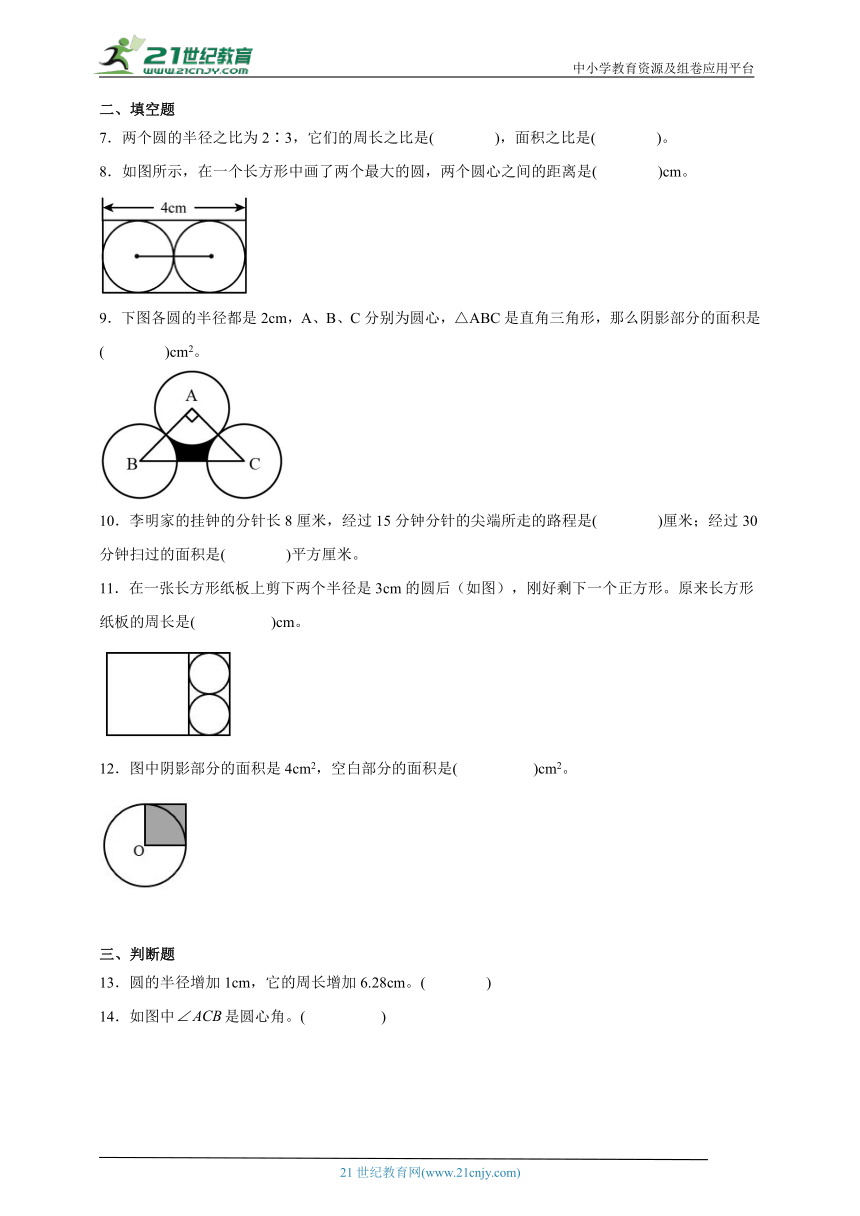
8.如图所示,在一个长方形中画了两个最大的圆,两个圆心之间的距离是( )cm。
9.下图各圆的半径都是2cm,A、B、C分别为圆心,△ABC是直角三角形,那么阴影部分的面积是( )cm2。
10.李明家的挂钟的分针长8厘米,经过15分钟分针的尖端所走的路程是( )厘米;经过30分钟扫过的面积是( )平方厘米。
11.在一张长方形纸板上剪下两个半径是3cm的圆后(如图),刚好剩下一个正方形。原来长方形纸板的周长是( )cm。
12.图中阴影部分的面积是4cm2,空白部分的面积是( )cm2。
三、判断题
13.圆的半径增加1cm,它的周长增加6.28cm。( )
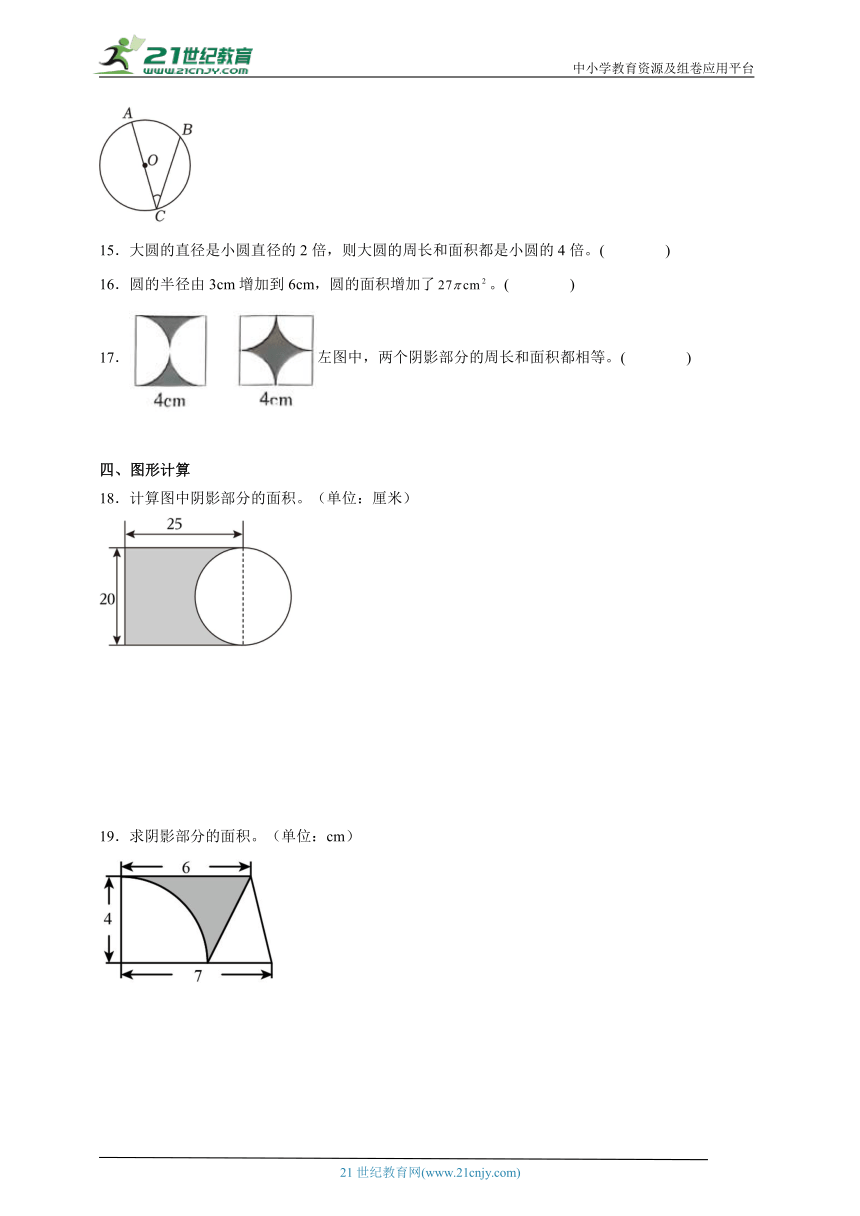
14.如图中是圆心角。( )
15.大圆的直径是小圆直径的2倍,则大圆的周长和面积都是小圆的4倍。( )
16.圆的半径由3cm增加到6cm,圆的面积增加了。( )
17.左图中,两个阴影部分的周长和面积都相等。( )
四、图形计算
18.计算图中阴影部分的面积。(单位:厘米)
19.求阴影部分的面积。(单位:cm)
五、解答题
20.文体中心有一个圆形表演台,周长56.52米。现在把舞台的半径加宽1米,比原来的面积增加多少?(π取3.14)
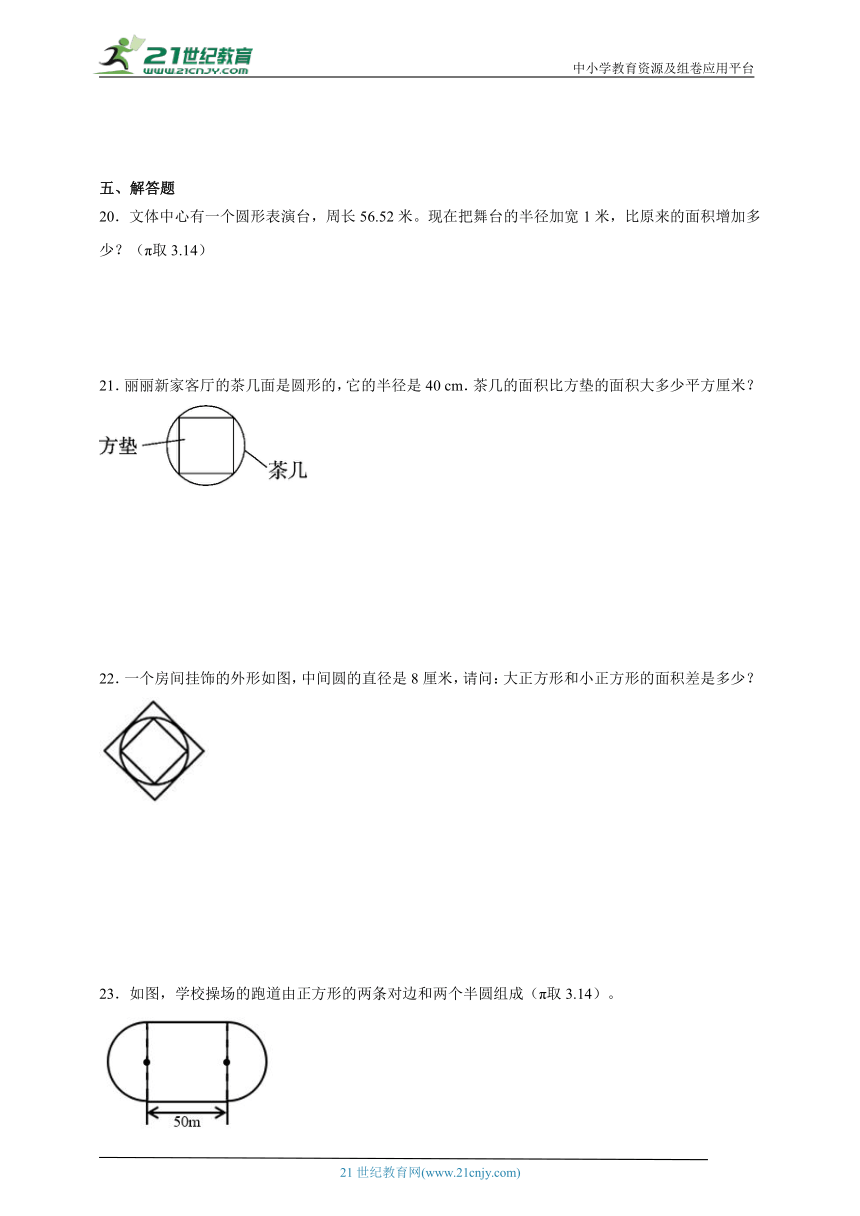
21.丽丽新家客厅的茶几面是圆形的,它的半径是40 cm.茶几的面积比方垫的面积大多少平方厘米?
22.一个房间挂饰的外形如图,中间圆的直径是8厘米,请问:大正方形和小正方形的面积差是多少?
23.如图,学校操场的跑道由正方形的两条对边和两个半圆组成(π取3.14)。
(1)跑道一周的长度是多少米?
(2)操场的占地面积是多少平方米?
24.(1)请你在方格里分别描出A(2,5)、B(8,5)、C(8,2)、D(2,2)各点依次连接起来,试着在连接的图形里画出一个最大的半圆。
(2)把图形里剩余的部分用阴影部分表示,并求出阴影部分的面积。(小正方形的边长为1厘米。)
参考答案:
1.C
【分析】根据题意可知,正方形内画最大的圆,圆的直径等于正方形的边长;设正方形的边长为2,则圆的直径也等于2,根据圆的面积公式:面积=π×半径2;正方形面积公式:面积=边长×边长,代入数据,求出圆的面积和正方形的面积;再根据比的意义,用圆的面积∶正方形的面积,即可解答。
【详解】设正方形的边长为2,则圆的直径是2。
[π×(2÷2)2]∶(2×2)
=[π×12]∶4
=[π×1]∶4
=π∶4
=
如图,在正方形里画一个最大的圆,圆的面积与正方形面积的比是。
故答案为:C
【点睛】解答本题的关键明确正方形内画最大的圆,圆的直径与正方形边长的关系。
2.B
【分析】圆周率的含义:圆的周长和它直径的比值,叫做圆周率,用字母π表示,π是一个无限不循环小数;据此进行分析解答即可。
【详解】由分析可得:圆周率是圆的周长和它直径的比值,即圆周率是圆周长和直径的倍数关系。
故答案为:B
【点睛】此题考查的目的是理解圆周率的意义。
3.C
【分析】根据圆的面积公式S=πr2,求出两个圆的面积之差即为增加的面积。
【详解】π×42-π×32
=16π-9π
=7π(cm2)
圆的半径由3cm增加到4cm,这个圆的面积增加了7πcm2。
故答案为:C
【点睛】本题主要考查圆的面积公式,此题计算时还可以运用乘法分配律计算。
4.B
【分析】①真分数的分子小于分母,把真分数的分子、分母交换位置,得到的分数是假分数,假分数大于真分数。
②一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小。
③当被除数不等于0时,若除数大于1,则商小于被除数;若除数小于1(0除外),则商大于被除数;若除数等于1,则商等于被除数。
④求一个数比另一个数少几分之几的解题方法:两数差量÷单位“1”的量。据此用(5-4)÷5可求出大牛比小牛少几分之几。
⑤圆周率是任意一个圆的周长与它的直径的比值,用字母表示,这个比值是一个固定的数,它是一个无限不循环小数,=3.1415926535……。
⑥用4个圆心角都是90°且半径相等的扇形,一定可以拼成一个圆。
【详解】①真分数的倒数是假分数,假分数大于真分数,所以一个真分数的倒数一定比这个真分数大。①中的说法正确。
②一个数(0除外)乘大于1的假分数,积比原来的数大。所以一个数乘分数的积不一定比原来的数小。②中的说法错误。
③一个数(0除外)除以大于1的假分数,则商小于被除数;所以一个数除以分数的商不一定比原来的数大。③中的说法错误。
④(5-4)÷5=1÷5=,所以大牛和小牛的数量比是4∶5,表示大牛比小牛少。④中的说法正确。
⑤圆周率=3.1415926535……。⑤中的说法错误。
⑥如下图:当4个圆心角都是90°的扇形的半径不相等时,不可以拼成一个圆。⑥中的说法错误。
所以说法错误的有②③⑤⑥。
故答案为:B
【点睛】此题考查了倒数的意义、积与乘数的大小关系、商与被除数的大小关系、求一个数比另一个数少几分之几的问题、圆周率的意义、扇形与圆的关系。
5.A
【分析】根据圆的周长公式C=πd可知:一个圆的直径扩大到原来的n倍,周长也扩大到原来的n倍,据此解答即可。
【详解】一个圆的直径扩大4倍,它的周长扩大4倍。
故答案为:A
【点睛】本题主要考查了圆的直径、周长与半径成正比例关系的灵活应用。
6.D
【分析】先根据圆的面积公式:S=,代入数据求出这块圆形菜地的半径,再根据圆的周长公式:C=,代入半径的数据,即可求出篱笆的长度。
【详解】r2=706.5÷3.14=225
因为15×15=225,
所以圆的半径为15米。
2×3.14×15=94.2(米)
即他应该用94.2米长篱笆来围。
故答案为:D
【点睛】此题的解题关键是灵活运用圆的周长和圆的面积公式求解。
7. 2∶3 4∶9
【分析】假设出两个圆的半径,利用“”和“”分别求出它们的周长和面积,最后根据比的意义求出它们的周长比和面积比,据此解答。
【详解】假设这两个圆的半径分别为和。
周长1:=
周长2:=
∶
=4∶6
=(4÷2)∶(6÷2)
=2∶3
面积1:
=
=
面积2:
=
=
∶
=4∶9
所以,两个圆的半径之比为2∶3,它们的周长之比是2∶3,面积之比是4∶9。
【点睛】熟练掌握圆的周长和面积计算公式是解答题目的关键。
8.2
【分析】看图可知,两个圆心之间的距离=一个圆的直径,圆的直径=长方形的长÷2,据此列式计算。
【详解】4÷2=2(cm)
两个圆心之间的距离是2cm。
【点睛】关键是看懂图示,理解圆和长方形之间的关系。
9.1.72
【分析】由图可知:直角三角形的两条直角边均等于圆的直径,据此将数据代入三角形面积公式:S=ah÷2求出三角形的面积;根据三角形的内角和是180°且圆的半径相等可知:三角形内空白部分可拼接成半径是2cm的半圆,将数据代入圆的面积公式:S=πr2求出空白部分的面积,最后用三角形面积-空白部分面积即可求出阴影部分面积。
【详解】(2×2)×(2×2)÷2-3.14×22÷2
=4×4÷2-3.14×4÷2
=16÷2-12.56÷2
=8-6.28
=1.72(cm2)
阴影部分的面积是1.72cm2。
【点睛】理解三角形内空白部分可拼接成半径是2cm的半圆是解题的关键。
10. 12.56 100.48
【分析】根据圆的周长公式:C=2πr,据此求出挂钟的周长,经过15分钟,所形成的轨迹是一个圆,据此进行即可;分针扫过的面积是以分针长为半径的圆的面积的一半,据此解答。
【详解】3.14×2×8×
=6.28×8×
=50.24×
=12.56(厘米)
3.14×82×
=3.14×64×
=200.96×
=100.48(平方厘米)
则经过15分钟分针的尖端所走的路程是12.56厘米;经过30分钟扫过的面积是100.48平方厘米。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
11.60
【分析】已知圆的半径是3cm,则圆的直径是6cm;从图中可知,长方形的宽等于圆的直径的2倍,即12cm;剪下两个半径是3cm的圆后,刚好剩下一个正方形,则正方形的边长是12cm;
从图中可知,原来长方形的长等于正方形的边长加上圆的直径,由此得出原来长方形的长是(12+6)cm,再根据长方形的周长=(长+宽)×2,代入数据计算,即可求解。
【详解】圆的直径:3×2=6(cm)
长方形的宽:6×2=12(cm)
长方形的长:12+6=18(cm)
长方形的周长:
(18+12)×2
=30×2
=60(cm)
原来长方形纸板的周长是60cm。
【点睛】解题的关键是找出长方形的长、宽与圆的直径之间的关系,再根据长方形周长公式求解。
12.9.42
【分析】阴影部分是个正方形,正方形边长=圆的半径,正方形面积=边长×边长=r×r=4 cm2,空白部分是个圆,根据圆的面积=πr2,圆的面积×=空白部分的面积。
【详解】3.14×4×=9.42(cm2)
空白部分的面积是9.42cm2。
【点睛】关键是掌握并灵活运用圆和正方形的面积公式。
13.√
【分析】假设圆的半径为r,根据圆的周长公式,表示出原来圆的周长为,圆的半径增加1cm后,则圆的半径为(r+1)cm,利用圆的周长公式求出增加后圆的周长,再减去原来圆的周长,即可得解。
【详解】假设圆的半径为r,圆的周长为,
增加后圆的周长==
=
=2×3.14
=6.28(cm)
即它的周长增加6.28cm。
故答案为:√
【点睛】此题的解题关键是灵活运用圆的周长公式求解。
14.×
【分析】圆心角的顶点在圆心上,而图中的顶点不在圆心上,所以不是圆心角。
【详解】的顶点不在圆心上,所以不是圆心角,题干说法错误。
故答案为:
【点睛】本题考查圆心角的定义,圆心角的圆心在圆心上。
15.×
【分析】根据题意,假设小圆的半径为r,则大圆的直径为4r,则小圆的直径为2r, 再根据圆的周长公式为:,圆的面积公式:,分别表示出大圆和小圆的周长及大圆和小圆的面积,然后用除法列式即可。
【详解】解:设小圆的半径为r,则大圆的直径为4r,则小圆的直径为2r,可得:
÷=2
÷
=÷
=÷
=4
所以,大圆的直径是小圆直径的2倍,则大圆的周长是小圆的2倍、大圆的面积是小圆的4倍,故原题干说法错误。
故答案为:×
【点睛】解答此题应先设出小圆的半径,进而用字母表示出大圆的直径,进而根据圆的周长和面积计算公式,分别求出两个圆的周长和面积,再根据求一个数是另一个数的几倍,用除法列式解答。
16.√
【分析】根据圆的面积公式: ,先分别计算出半径是3cm和半径是6cm的圆的面积,再利用减法求出面积增加了多少。
【详解】×62-×32
=×36-×9
=27(cm2)
所以,圆的半径由3cm增加到6cm,圆的面积增加了27cm2。
故答案为:√
【点睛】此题主要考查的是圆的面积公式的灵活应用。
17.×
【分析】第一个图形阴影部分的周长等于直径为4厘米的圆的周长加上两条正方形的边长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解;
第二个图形阴影部分的周长等于直径为4厘米的圆的周长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解。
【详解】第一个图形阴影部分的周长:
3.14×4+4×2
=12.56+8
=20.56(厘米)
第一个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
第二个图形阴影部分的周长:
3.14×4=12.56(厘米)
第二个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
所以两个阴影部分的周长不相等,面积相等。原题说法错误。
故答案为:×
【点睛】此题的解题关键是灵活运用圆的周长和面积公式求解。
18.343平方厘米
【分析】利用长方形的面积公式:S=a×b,长为25厘米,宽为20厘米,代入求出长方形的面积,圆的直径为20厘米,半径为(20÷2)厘米,利用圆的面积公式,再除以2,求出空白部分半圆的面积,用长方形的面积减去半圆的面积,即可求出阴影部分的面积。
【详解】25×20-3.14×÷2
=500-3.14×÷2
=500-3.14×100÷2
=500-157
=343(平方厘米)
19.7.44
【分析】观察图形可知,阴影部分的面积等于梯形的面积减去半径为4cm的圆的面积的,再减去底为(7-4)cm,高为4cm的三角形的面积,根据圆的面积公式:S=πr2,三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
【详解】(6+7)×4÷2
=13×4÷2
=52÷2
=26()
(7-4)×4÷2
=3×4÷2
=12÷2
=6()
3.14×
=3.14×16
=50.24
=12.56()
26-12.56-6
=13.44-6
=7.44()
20.59.66平方米
【分析】根据圆的周长公式:C=,代入数据求出原来圆形表演台的半径为9米,把舞台的半径加宽1米,此时圆的半径为10米,求比原来增加的面积,实际上求圆环的面积,利用圆环的面积公式:S=,代入数据,即可求出增加的面积。
【详解】56.52÷2÷3.14=9(米)
9+1=10(米)
3.14×(102-92)
=3.14×(100-81)
=3.14×19
=59.66(平方米)
答:比原来的面积增加了59.66平方米。
【点睛】此题的解题关键是灵活运用圆的周长以及圆环的面积公式求解。
21.1824平方厘米
【详解】40×2=80(cm)
3.14×402-80×40÷2×2
=5024-3200
=1824(cm2)
把圆内的正方形分成两个三角形,可求出此正方形的面积.
22.32平方厘米
【分析】如解答中图形连接小正方形的对角线,把圆的内接正方形分成4个小等腰直角三角形,每个等腰直角三角形的直角边长都等于圆的半径,根据三角形的面积公式:S=ah÷2,即可求出一个三角形的面积,再乘4就是小正方形的面积;大正方形边长等于圆的直径,用正方形的面积公式S=a×a求出大正方形的面积;用大正方形的面积减小正方形的面积即可求解。
【详解】如图:连接小正方形的对角线,
8×8-(8÷2)×(8÷2)÷2×4
=64-4×4÷2×4
=64-16÷2×4
=64-8×4
=64-32
=32(平方厘米)
答:大正方形和小正方形的面积差是32平方厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键确定小正方形的面积等于4个等腰直角三角形的面积及大正方形的边长等于圆的直径。
23.(1)257米
(2)4462.5平方米
【分析】(1)观察图形可知,两个半圆组成一个圆,跑道一周的长度=圆的周长+2条直跑道,根据圆的周长公式C=πd,代入数据计算即可。
(2)观察图形可知,两个半圆组成一个圆,操场的占地面积=正方形的面积+圆的面积,根据圆的面积公式S=πr2,代入数据计算即可。
【详解】(1)3.14×50+50×2
=157+100
=257(米)
答:跑道一周的长度是257米。
(2)正方形的面积:
50×50=2500(平方米)
圆的面积:
3.14×(50÷2)2
=3.14×625
=1962.5(平方米)
一共:2500+1962.5=4462.5(平方米)
答:操场的占地面积是4462.5平方米。
【点睛】本题考查组合图形周长和面积的求法,分析组合图形是由哪些基本图形组成,再根据图形的周长、面积公式解答。
24.(1)见详解;(2)3.87平方厘米
【分析】(1)用数对表示位置时,前一个数表示第几列,后一个数表示第几行,据此依次连接A、B、C、D各点后发现,这是一个长方形,宽有3厘米,长有6厘米,要在这个长方形中画一个最大的半圆,则以半径为3厘米画出即可;
(2)根据长方形的面积=长×宽,用6×3即可求出长方形的面积,再根据圆面积=πr2,用3.14×32÷2即可求出半圆的面积,最后求出它们的差即可。
【详解】(1)根据题意连接,可得图形是一个长方形,
长:8-2=6(厘米)
宽:5-2=3(厘米)
在这个长方形中画一个最大的半圆,则这个半圆的半径是3厘米,如图:
(2)6×3-3.14×32÷2
=6×3-3.14×9÷2
=18-14.13
=3.87(平方厘米)
阴影部分的面积是3.87平方厘米。
【点睛】本题考查了根据数对找位置,以及圆面积公式、长方形面积公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第5单元圆易错精选题-数学六年级上册人教版
一、选择题
1.如图,在正方形里画一个最大的圆,圆的面积与正方形面积的比是( )。
A. B. C. D.
2.关于“圆周率”的认识,你同意的是( )。
A.圆周率是圆的周长
B.圆周率是圆周长和直径的倍数关系
C.圆周率是圆周长和半径的倍数关系
D.圆周率是圆面积和直径的倍数关系
3.圆的半径由3cm增加到4cm,这个圆的面积增加了( )cm2。
A.1 B.7 C.7π D.π
4.下列说法错误的是( )。
①一个真分数的倒数一定比这个真分数大。
②一个数乘分数的积一定比原来的数小。
③一个数除以分数的商一定比原来的数大。
④大牛和小牛的数量比是4∶5,表示大牛比小牛少。
⑤圆周率π就是3.14。
⑥用4个圆心角都是90°的扇形,一定可以拼成一个圆。
A.②③④⑤⑥ B.②③⑤⑥ C.① D.②③⑤
5.一个圆的直径扩大4倍,它的周长扩大( )倍。
A.4 B.16 C.2 D.8
6.小东想在空地上围出一块面积为706.5平方米的圆形土地来种菜他应该用多长的篱笆来围(圆周率取3.14)。( )
A.78.5米 B.87.5米 C.92.4米 D.94.2米
二、填空题
7.两个圆的半径之比为2∶3,它们的周长之比是( ),面积之比是( )。
8.如图所示,在一个长方形中画了两个最大的圆,两个圆心之间的距离是( )cm。
9.下图各圆的半径都是2cm,A、B、C分别为圆心,△ABC是直角三角形,那么阴影部分的面积是( )cm2。
10.李明家的挂钟的分针长8厘米,经过15分钟分针的尖端所走的路程是( )厘米;经过30分钟扫过的面积是( )平方厘米。
11.在一张长方形纸板上剪下两个半径是3cm的圆后(如图),刚好剩下一个正方形。原来长方形纸板的周长是( )cm。
12.图中阴影部分的面积是4cm2,空白部分的面积是( )cm2。
三、判断题
13.圆的半径增加1cm,它的周长增加6.28cm。( )
14.如图中是圆心角。( )
15.大圆的直径是小圆直径的2倍,则大圆的周长和面积都是小圆的4倍。( )
16.圆的半径由3cm增加到6cm,圆的面积增加了。( )
17.左图中,两个阴影部分的周长和面积都相等。( )
四、图形计算
18.计算图中阴影部分的面积。(单位:厘米)
19.求阴影部分的面积。(单位:cm)
五、解答题
20.文体中心有一个圆形表演台,周长56.52米。现在把舞台的半径加宽1米,比原来的面积增加多少?(π取3.14)
21.丽丽新家客厅的茶几面是圆形的,它的半径是40 cm.茶几的面积比方垫的面积大多少平方厘米?
22.一个房间挂饰的外形如图,中间圆的直径是8厘米,请问:大正方形和小正方形的面积差是多少?
23.如图,学校操场的跑道由正方形的两条对边和两个半圆组成(π取3.14)。
(1)跑道一周的长度是多少米?
(2)操场的占地面积是多少平方米?
24.(1)请你在方格里分别描出A(2,5)、B(8,5)、C(8,2)、D(2,2)各点依次连接起来,试着在连接的图形里画出一个最大的半圆。
(2)把图形里剩余的部分用阴影部分表示,并求出阴影部分的面积。(小正方形的边长为1厘米。)
参考答案:
1.C
【分析】根据题意可知,正方形内画最大的圆,圆的直径等于正方形的边长;设正方形的边长为2,则圆的直径也等于2,根据圆的面积公式:面积=π×半径2;正方形面积公式:面积=边长×边长,代入数据,求出圆的面积和正方形的面积;再根据比的意义,用圆的面积∶正方形的面积,即可解答。
【详解】设正方形的边长为2,则圆的直径是2。
[π×(2÷2)2]∶(2×2)
=[π×12]∶4
=[π×1]∶4
=π∶4
=
如图,在正方形里画一个最大的圆,圆的面积与正方形面积的比是。
故答案为:C
【点睛】解答本题的关键明确正方形内画最大的圆,圆的直径与正方形边长的关系。
2.B
【分析】圆周率的含义:圆的周长和它直径的比值,叫做圆周率,用字母π表示,π是一个无限不循环小数;据此进行分析解答即可。
【详解】由分析可得:圆周率是圆的周长和它直径的比值,即圆周率是圆周长和直径的倍数关系。
故答案为:B
【点睛】此题考查的目的是理解圆周率的意义。
3.C
【分析】根据圆的面积公式S=πr2,求出两个圆的面积之差即为增加的面积。
【详解】π×42-π×32
=16π-9π
=7π(cm2)
圆的半径由3cm增加到4cm,这个圆的面积增加了7πcm2。
故答案为:C
【点睛】本题主要考查圆的面积公式,此题计算时还可以运用乘法分配律计算。
4.B
【分析】①真分数的分子小于分母,把真分数的分子、分母交换位置,得到的分数是假分数,假分数大于真分数。
②一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小。
③当被除数不等于0时,若除数大于1,则商小于被除数;若除数小于1(0除外),则商大于被除数;若除数等于1,则商等于被除数。
④求一个数比另一个数少几分之几的解题方法:两数差量÷单位“1”的量。据此用(5-4)÷5可求出大牛比小牛少几分之几。
⑤圆周率是任意一个圆的周长与它的直径的比值,用字母表示,这个比值是一个固定的数,它是一个无限不循环小数,=3.1415926535……。
⑥用4个圆心角都是90°且半径相等的扇形,一定可以拼成一个圆。
【详解】①真分数的倒数是假分数,假分数大于真分数,所以一个真分数的倒数一定比这个真分数大。①中的说法正确。
②一个数(0除外)乘大于1的假分数,积比原来的数大。所以一个数乘分数的积不一定比原来的数小。②中的说法错误。
③一个数(0除外)除以大于1的假分数,则商小于被除数;所以一个数除以分数的商不一定比原来的数大。③中的说法错误。
④(5-4)÷5=1÷5=,所以大牛和小牛的数量比是4∶5,表示大牛比小牛少。④中的说法正确。
⑤圆周率=3.1415926535……。⑤中的说法错误。
⑥如下图:当4个圆心角都是90°的扇形的半径不相等时,不可以拼成一个圆。⑥中的说法错误。
所以说法错误的有②③⑤⑥。
故答案为:B
【点睛】此题考查了倒数的意义、积与乘数的大小关系、商与被除数的大小关系、求一个数比另一个数少几分之几的问题、圆周率的意义、扇形与圆的关系。
5.A
【分析】根据圆的周长公式C=πd可知:一个圆的直径扩大到原来的n倍,周长也扩大到原来的n倍,据此解答即可。
【详解】一个圆的直径扩大4倍,它的周长扩大4倍。
故答案为:A
【点睛】本题主要考查了圆的直径、周长与半径成正比例关系的灵活应用。
6.D
【分析】先根据圆的面积公式:S=,代入数据求出这块圆形菜地的半径,再根据圆的周长公式:C=,代入半径的数据,即可求出篱笆的长度。
【详解】r2=706.5÷3.14=225
因为15×15=225,
所以圆的半径为15米。
2×3.14×15=94.2(米)
即他应该用94.2米长篱笆来围。
故答案为:D
【点睛】此题的解题关键是灵活运用圆的周长和圆的面积公式求解。
7. 2∶3 4∶9
【分析】假设出两个圆的半径,利用“”和“”分别求出它们的周长和面积,最后根据比的意义求出它们的周长比和面积比,据此解答。
【详解】假设这两个圆的半径分别为和。
周长1:=
周长2:=
∶
=4∶6
=(4÷2)∶(6÷2)
=2∶3
面积1:
=
=
面积2:
=
=
∶
=4∶9
所以,两个圆的半径之比为2∶3,它们的周长之比是2∶3,面积之比是4∶9。
【点睛】熟练掌握圆的周长和面积计算公式是解答题目的关键。
8.2
【分析】看图可知,两个圆心之间的距离=一个圆的直径,圆的直径=长方形的长÷2,据此列式计算。
【详解】4÷2=2(cm)
两个圆心之间的距离是2cm。
【点睛】关键是看懂图示,理解圆和长方形之间的关系。
9.1.72
【分析】由图可知:直角三角形的两条直角边均等于圆的直径,据此将数据代入三角形面积公式:S=ah÷2求出三角形的面积;根据三角形的内角和是180°且圆的半径相等可知:三角形内空白部分可拼接成半径是2cm的半圆,将数据代入圆的面积公式:S=πr2求出空白部分的面积,最后用三角形面积-空白部分面积即可求出阴影部分面积。
【详解】(2×2)×(2×2)÷2-3.14×22÷2
=4×4÷2-3.14×4÷2
=16÷2-12.56÷2
=8-6.28
=1.72(cm2)
阴影部分的面积是1.72cm2。
【点睛】理解三角形内空白部分可拼接成半径是2cm的半圆是解题的关键。
10. 12.56 100.48
【分析】根据圆的周长公式:C=2πr,据此求出挂钟的周长,经过15分钟,所形成的轨迹是一个圆,据此进行即可;分针扫过的面积是以分针长为半径的圆的面积的一半,据此解答。
【详解】3.14×2×8×
=6.28×8×
=50.24×
=12.56(厘米)
3.14×82×
=3.14×64×
=200.96×
=100.48(平方厘米)
则经过15分钟分针的尖端所走的路程是12.56厘米;经过30分钟扫过的面积是100.48平方厘米。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
11.60
【分析】已知圆的半径是3cm,则圆的直径是6cm;从图中可知,长方形的宽等于圆的直径的2倍,即12cm;剪下两个半径是3cm的圆后,刚好剩下一个正方形,则正方形的边长是12cm;
从图中可知,原来长方形的长等于正方形的边长加上圆的直径,由此得出原来长方形的长是(12+6)cm,再根据长方形的周长=(长+宽)×2,代入数据计算,即可求解。
【详解】圆的直径:3×2=6(cm)
长方形的宽:6×2=12(cm)
长方形的长:12+6=18(cm)
长方形的周长:
(18+12)×2
=30×2
=60(cm)
原来长方形纸板的周长是60cm。
【点睛】解题的关键是找出长方形的长、宽与圆的直径之间的关系,再根据长方形周长公式求解。
12.9.42
【分析】阴影部分是个正方形,正方形边长=圆的半径,正方形面积=边长×边长=r×r=4 cm2,空白部分是个圆,根据圆的面积=πr2,圆的面积×=空白部分的面积。
【详解】3.14×4×=9.42(cm2)
空白部分的面积是9.42cm2。
【点睛】关键是掌握并灵活运用圆和正方形的面积公式。
13.√
【分析】假设圆的半径为r,根据圆的周长公式,表示出原来圆的周长为,圆的半径增加1cm后,则圆的半径为(r+1)cm,利用圆的周长公式求出增加后圆的周长,再减去原来圆的周长,即可得解。
【详解】假设圆的半径为r,圆的周长为,
增加后圆的周长==
=
=2×3.14
=6.28(cm)
即它的周长增加6.28cm。
故答案为:√
【点睛】此题的解题关键是灵活运用圆的周长公式求解。
14.×
【分析】圆心角的顶点在圆心上,而图中的顶点不在圆心上,所以不是圆心角。
【详解】的顶点不在圆心上,所以不是圆心角,题干说法错误。
故答案为:
【点睛】本题考查圆心角的定义,圆心角的圆心在圆心上。
15.×
【分析】根据题意,假设小圆的半径为r,则大圆的直径为4r,则小圆的直径为2r, 再根据圆的周长公式为:,圆的面积公式:,分别表示出大圆和小圆的周长及大圆和小圆的面积,然后用除法列式即可。
【详解】解:设小圆的半径为r,则大圆的直径为4r,则小圆的直径为2r,可得:
÷=2
÷
=÷
=÷
=4
所以,大圆的直径是小圆直径的2倍,则大圆的周长是小圆的2倍、大圆的面积是小圆的4倍,故原题干说法错误。
故答案为:×
【点睛】解答此题应先设出小圆的半径,进而用字母表示出大圆的直径,进而根据圆的周长和面积计算公式,分别求出两个圆的周长和面积,再根据求一个数是另一个数的几倍,用除法列式解答。
16.√
【分析】根据圆的面积公式: ,先分别计算出半径是3cm和半径是6cm的圆的面积,再利用减法求出面积增加了多少。
【详解】×62-×32
=×36-×9
=27(cm2)
所以,圆的半径由3cm增加到6cm,圆的面积增加了27cm2。
故答案为:√
【点睛】此题主要考查的是圆的面积公式的灵活应用。
17.×
【分析】第一个图形阴影部分的周长等于直径为4厘米的圆的周长加上两条正方形的边长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解;
第二个图形阴影部分的周长等于直径为4厘米的圆的周长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解。
【详解】第一个图形阴影部分的周长:
3.14×4+4×2
=12.56+8
=20.56(厘米)
第一个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
第二个图形阴影部分的周长:
3.14×4=12.56(厘米)
第二个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
所以两个阴影部分的周长不相等,面积相等。原题说法错误。
故答案为:×
【点睛】此题的解题关键是灵活运用圆的周长和面积公式求解。
18.343平方厘米
【分析】利用长方形的面积公式:S=a×b,长为25厘米,宽为20厘米,代入求出长方形的面积,圆的直径为20厘米,半径为(20÷2)厘米,利用圆的面积公式,再除以2,求出空白部分半圆的面积,用长方形的面积减去半圆的面积,即可求出阴影部分的面积。
【详解】25×20-3.14×÷2
=500-3.14×÷2
=500-3.14×100÷2
=500-157
=343(平方厘米)
19.7.44
【分析】观察图形可知,阴影部分的面积等于梯形的面积减去半径为4cm的圆的面积的,再减去底为(7-4)cm,高为4cm的三角形的面积,根据圆的面积公式:S=πr2,三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
【详解】(6+7)×4÷2
=13×4÷2
=52÷2
=26()
(7-4)×4÷2
=3×4÷2
=12÷2
=6()
3.14×
=3.14×16
=50.24
=12.56()
26-12.56-6
=13.44-6
=7.44()
20.59.66平方米
【分析】根据圆的周长公式:C=,代入数据求出原来圆形表演台的半径为9米,把舞台的半径加宽1米,此时圆的半径为10米,求比原来增加的面积,实际上求圆环的面积,利用圆环的面积公式:S=,代入数据,即可求出增加的面积。
【详解】56.52÷2÷3.14=9(米)
9+1=10(米)
3.14×(102-92)
=3.14×(100-81)
=3.14×19
=59.66(平方米)
答:比原来的面积增加了59.66平方米。
【点睛】此题的解题关键是灵活运用圆的周长以及圆环的面积公式求解。
21.1824平方厘米
【详解】40×2=80(cm)
3.14×402-80×40÷2×2
=5024-3200
=1824(cm2)
把圆内的正方形分成两个三角形,可求出此正方形的面积.
22.32平方厘米
【分析】如解答中图形连接小正方形的对角线,把圆的内接正方形分成4个小等腰直角三角形,每个等腰直角三角形的直角边长都等于圆的半径,根据三角形的面积公式:S=ah÷2,即可求出一个三角形的面积,再乘4就是小正方形的面积;大正方形边长等于圆的直径,用正方形的面积公式S=a×a求出大正方形的面积;用大正方形的面积减小正方形的面积即可求解。
【详解】如图:连接小正方形的对角线,
8×8-(8÷2)×(8÷2)÷2×4
=64-4×4÷2×4
=64-16÷2×4
=64-8×4
=64-32
=32(平方厘米)
答:大正方形和小正方形的面积差是32平方厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键确定小正方形的面积等于4个等腰直角三角形的面积及大正方形的边长等于圆的直径。
23.(1)257米
(2)4462.5平方米
【分析】(1)观察图形可知,两个半圆组成一个圆,跑道一周的长度=圆的周长+2条直跑道,根据圆的周长公式C=πd,代入数据计算即可。
(2)观察图形可知,两个半圆组成一个圆,操场的占地面积=正方形的面积+圆的面积,根据圆的面积公式S=πr2,代入数据计算即可。
【详解】(1)3.14×50+50×2
=157+100
=257(米)
答:跑道一周的长度是257米。
(2)正方形的面积:
50×50=2500(平方米)
圆的面积:
3.14×(50÷2)2
=3.14×625
=1962.5(平方米)
一共:2500+1962.5=4462.5(平方米)
答:操场的占地面积是4462.5平方米。
【点睛】本题考查组合图形周长和面积的求法,分析组合图形是由哪些基本图形组成,再根据图形的周长、面积公式解答。
24.(1)见详解;(2)3.87平方厘米
【分析】(1)用数对表示位置时,前一个数表示第几列,后一个数表示第几行,据此依次连接A、B、C、D各点后发现,这是一个长方形,宽有3厘米,长有6厘米,要在这个长方形中画一个最大的半圆,则以半径为3厘米画出即可;
(2)根据长方形的面积=长×宽,用6×3即可求出长方形的面积,再根据圆面积=πr2,用3.14×32÷2即可求出半圆的面积,最后求出它们的差即可。
【详解】(1)根据题意连接,可得图形是一个长方形,
长:8-2=6(厘米)
宽:5-2=3(厘米)
在这个长方形中画一个最大的半圆,则这个半圆的半径是3厘米,如图:
(2)6×3-3.14×32÷2
=6×3-3.14×9÷2
=18-14.13
=3.87(平方厘米)
阴影部分的面积是3.87平方厘米。
【点睛】本题考查了根据数对找位置,以及圆面积公式、长方形面积公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
