5.4.2 正弦函数、余弦函数的性质(第一课时)
文档属性
| 名称 | 5.4.2 正弦函数、余弦函数的性质(第一课时) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 12:42:54 | ||
图片预览






文档简介
(共26张PPT)
第5章 三角函数
5.4 三角函数的图象和性质
5.4.2 正弦函数、余弦函数的性质(第一课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.了解周期函数、周期、最小正周期的定义; 1.数学抽象素养.
2.会求正弦函数、余弦函数 的周期; 2.直观想象素养、逻辑推理素养.
3.掌握函数、的奇偶性,会判定简单三角函数的奇偶性. 3.逻辑推理素养.
温故知新
-32°
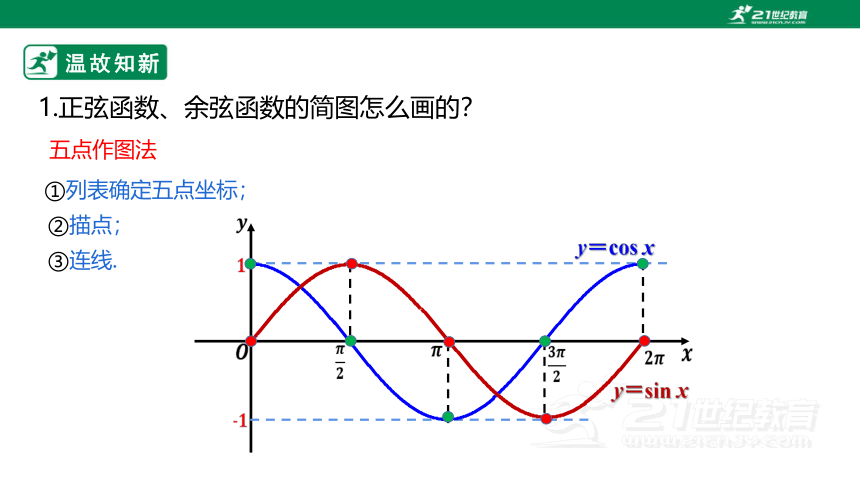
1.正弦函数、余弦函数的简图怎么画的?
五点作图法
①列表确定五点坐标;
②描点;
③连线.
y=sin x
y=cos x
温故知新
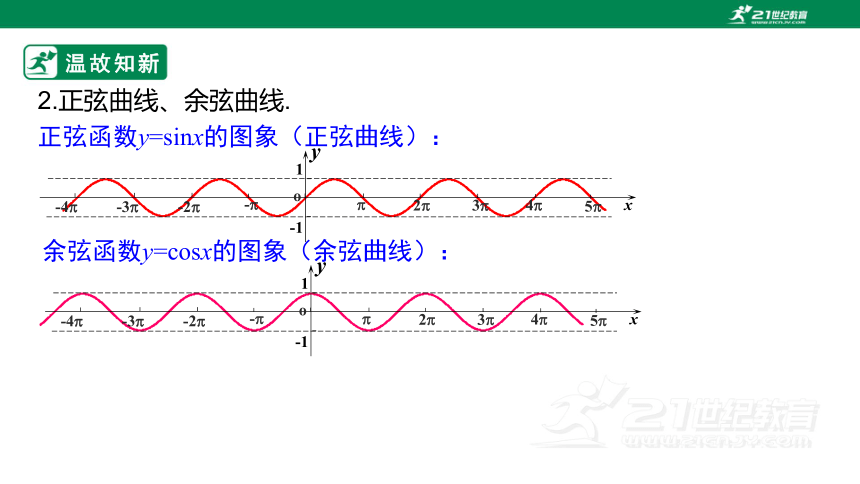
2.正弦曲线、余弦曲线.
正弦函数y=sinx的图象(正弦曲线):
x
y
o
-1
1
-
2
3
4
5
-2
-3
-4
余弦函数y=cosx的图象(余弦曲线):
x
y
o
-1
1
-
2
3
4
5
-2
-3
-4
新知探究
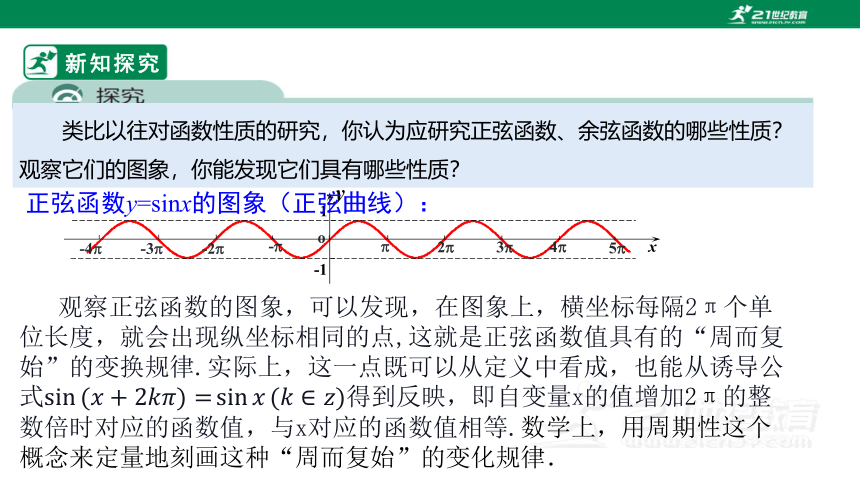
类比以往对函数性质的研究,你认为应研究正弦函数、余弦函数的哪些性质?观察它们的图象,你能发现它们具有哪些性质?
观察正弦函数的图象,可以发现,在图象上,横坐标每隔2π个单位长度,就会出现纵坐标相同的点,这就是正弦函数值具有的“周而复始”的变换规律.实际上,这一点既可以从定义中看成,也能从诱导公式得到反映,即自变量x的值增加2π的整数倍时对应的函数值,与x对应的函数值相等.数学上,用周期性这个概念来定量地刻画这种“周而复始”的变化规律.
x
y
o
-1
1
-
2
3
4
5
-2
-3
-4
正弦函数y=sinx的图象(正弦曲线):
新知探究
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且
f(x+T) = f(x),
那么函数f(x)就叫做周期函数(period function),T叫做这个函数的周期(period).
思考:2π是y=sin x,x∈R 的周期,那么4π,6π,-2π,-4π等是不是它的周期呢
可以发现,以及都是正弦函数的周期.事实上,,常数都是它的周期.
这说明周期函数的周期不止一个.
如果在周期函数所有周期中存在一个最小的正数,那么这个最小正数就叫做的最小正周期.
如果不加特别说明,周期一般都是指函数的最小正周期.
新知探究
注意:
⑴判定是周期函数,首先要满足“对每一个x∈D都有x+T∈D”.如果不满足这个条件,它肯定不是周期函数.
判定函数是不是周期函数?
⑵在满足“对每一个x∈D都有x+T∈D”前提下,满足这个条件,对都有.判定函数不是周期函数,只需找到一个,有即可.
⑶周期函数的周期不唯一.若T是函数f(x)的最小正周期,则kT(k∈Z,k≠0)也是函数f(x)的周期.而周期函数不一定有最小正周期,如常函数
,是周期函数,但没有最小正周期.
正弦余弦函数得周期性:正弦函数y=sin x 和余弦函数y=cos x 都是周期函数;2kπ (k∈Z且 k≠0) 都是它们的周期, 最小正周期 2π.
新知形成
解:
【例1】求下列函数的周期:
⑴, ⑵;
⑶.
⑴由正弦函数的周期为,得
有
分析:通常可以利用三角函数的周期性,通过代数变形,得出,而求出相应的周期.对, “3”作为sinx 的系数,不影响自变量x的变化.
由周期函数得定义可知,的周期为.
新知形成
解:
【例1】求下列函数的周期:
⑴, ⑵;
⑶.
⑵令,得, 则.
分析:对于⑵,应从余弦函数的周期性出发,通过代数变形得出.
由的周期为,得
于是
所以
由周期函数得定义可知,的周期为.
新知形成
解:
【例1】求下列函数的周期:
⑴, ⑵;
⑶.
⑶令,得, 则.
分析:对于⑶,应从正弦函数的周期性出发,通过代数变形得出
.
由的周期为,得
于是
所以
由周期函数得定义可知,的周期为.
新知形成
回归例1得解题过程,你能发现函数周期与函数解析式中的哪些有关吗?
函数的周期与解析式中只与系数有关.
对于函数的最小正周期.
设,有
即
=
的最小正周期.
函数或的周期都为.
新知探求
思考:观察正弦曲线和余弦曲线,看它们是否关于原点或y轴对称?能否由此判定它们的奇偶性 ?如何证明?
正弦曲线关于原点O 对称 ,正弦函数y=sinx,x∈R为奇函数 ;余弦曲线关于 y 轴对称,余弦函数y=cos x,x∈R为偶函数.
新知探求
正弦曲线关于原点O 对称 ,正弦函数y=sinx,x∈R为奇函数 ;余弦曲线关于 y 轴对称,余弦函数y=cos x,x∈R为偶函数.
证明:
正余弦函数的奇偶性
正弦函数是奇函数,余弦函数是偶函数.
新知探求
除坐标原点外,正弦函数图像是否还有其它对称中心,它们的位置特征是什么?
正弦函数图像关于点(成对称中心,均为函数图像与交点,任意两个对称中心横坐标相差.
=
=图像关于点(成对称中心.
新知探求
正弦函数图像是否为轴对称图形 对称轴是否唯一?它们的位置特征是什么?
正弦函数图像关于直线成轴对称,每条对称轴经过图像最高或最低点,任意两条对称轴之间相差.
又
=图像关于直线成轴对称.
新知探求
类比正弦函数,请你根据余弦函数图像分析余弦函数对称轴、对称中心.
余弦函数图像关于直线成轴对称,每条对称轴经过图像最高或最低点,任意两条对称轴之间相差.
余弦函数图像关于点(成对称中心,均为函数图像与交点,任意两个对称中心横坐标相差.
知道一个函数具有周期性和奇偶性,对研究它的图象和性质有什么帮助?
新知探求
【例2】判断下列函数的奇偶性:
⑴, ⑵;
⑶; ⑷
解:
⑴∵函数的定义域不关于原点对称,
∴此函数既不是奇函数,也不是偶函数.
⑵∵函数的定义域R关于原点对称,
又
而
∴此函数是奇函数.
新知探求
【例2】判断下列函数的奇偶性:
⑶; ⑷
解:
⑶∵函数的定义域为,关于原点对称.
⑷由得,即得此函数定义域为,关于原点对称.
又
而
∴此函数是奇函数.
∴此函数是偶函数.
又
而
初试身手
1.函数的最小正周期为( )
A. B. C. D.
2.函数的周期是 .
解:
1.对则函数的最小正周期为,故选C.
2.函数的周期.
C
初试身手
3.判断下列函数的奇偶性:
⑴; ⑵; ⑶.
解:
⑴此函数为非奇非偶函数.
⑵此函数为偶函数.
⑶此函数的定义域为,它关于原点对称.
又
而
则此函数为奇函数.
初试身手
4.下列函数中是奇函数,且最小正周期为的函数是( )
A. B. C. D.
5.函数是奇函数,且对,都有,又,则
= .
解:
4.4.函数 , 都为偶函数;又也为偶函数;对,它为奇函数,周期,故选D.
5.由已知得,对,
则得周期为.
则.
D
又因为为奇函数,
-1
课堂小结
1.求函数的最小正周期的常用方法:
2.判断函数的奇偶性,必须坚持“定义域优先”的原则,准确求函数定义域和将式子合理变形是解决此类问题的关键.如果定义域关于原点对称,再看f(-x)与f(x)的关系,从而判断奇偶性.
(1)定义法,即观察出周期,再用定义来验证;也可由函数所具有的某些性质推出使f(x+T)=f(x)成立的T.
(2)图象法,即作出y=f(x)的图象,观察图象可求出T,如y=|sin x|.
(3)结论法,函数y=Asin(ωx+φ)(其中A,ω,φ为常数,A≠0,ω>0,x∈R)的周期.
作业布置
作业:P203练习 第3,4题 P213 习题5.4 第2,3题.
补充:
1.(多选题)下列关于x的函数f(x)=sin(x+φ)的说法正确的是( )
A.对任意的φ,f(x)都是非奇非偶函数 B.存在φ,使f(x)是偶函数
C.存在φ,使f(x)是奇函数 D.对任意的φ,f(x)都不是偶函数
2.已知,则= .
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第5章 三角函数
5.4 三角函数的图象和性质
5.4.2 正弦函数、余弦函数的性质(第一课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.了解周期函数、周期、最小正周期的定义; 1.数学抽象素养.
2.会求正弦函数、余弦函数 的周期; 2.直观想象素养、逻辑推理素养.
3.掌握函数、的奇偶性,会判定简单三角函数的奇偶性. 3.逻辑推理素养.
温故知新
-32°
1.正弦函数、余弦函数的简图怎么画的?
五点作图法
①列表确定五点坐标;
②描点;
③连线.
y=sin x
y=cos x
温故知新
2.正弦曲线、余弦曲线.
正弦函数y=sinx的图象(正弦曲线):
x
y
o
-1
1
-
2
3
4
5
-2
-3
-4
余弦函数y=cosx的图象(余弦曲线):
x
y
o
-1
1
-
2
3
4
5
-2
-3
-4
新知探究
类比以往对函数性质的研究,你认为应研究正弦函数、余弦函数的哪些性质?观察它们的图象,你能发现它们具有哪些性质?
观察正弦函数的图象,可以发现,在图象上,横坐标每隔2π个单位长度,就会出现纵坐标相同的点,这就是正弦函数值具有的“周而复始”的变换规律.实际上,这一点既可以从定义中看成,也能从诱导公式得到反映,即自变量x的值增加2π的整数倍时对应的函数值,与x对应的函数值相等.数学上,用周期性这个概念来定量地刻画这种“周而复始”的变化规律.
x
y
o
-1
1
-
2
3
4
5
-2
-3
-4
正弦函数y=sinx的图象(正弦曲线):
新知探究
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且
f(x+T) = f(x),
那么函数f(x)就叫做周期函数(period function),T叫做这个函数的周期(period).
思考:2π是y=sin x,x∈R 的周期,那么4π,6π,-2π,-4π等是不是它的周期呢
可以发现,以及都是正弦函数的周期.事实上,,常数都是它的周期.
这说明周期函数的周期不止一个.
如果在周期函数所有周期中存在一个最小的正数,那么这个最小正数就叫做的最小正周期.
如果不加特别说明,周期一般都是指函数的最小正周期.
新知探究
注意:
⑴判定是周期函数,首先要满足“对每一个x∈D都有x+T∈D”.如果不满足这个条件,它肯定不是周期函数.
判定函数是不是周期函数?
⑵在满足“对每一个x∈D都有x+T∈D”前提下,满足这个条件,对都有.判定函数不是周期函数,只需找到一个,有即可.
⑶周期函数的周期不唯一.若T是函数f(x)的最小正周期,则kT(k∈Z,k≠0)也是函数f(x)的周期.而周期函数不一定有最小正周期,如常函数
,是周期函数,但没有最小正周期.
正弦余弦函数得周期性:正弦函数y=sin x 和余弦函数y=cos x 都是周期函数;2kπ (k∈Z且 k≠0) 都是它们的周期, 最小正周期 2π.
新知形成
解:
【例1】求下列函数的周期:
⑴, ⑵;
⑶.
⑴由正弦函数的周期为,得
有
分析:通常可以利用三角函数的周期性,通过代数变形,得出,而求出相应的周期.对, “3”作为sinx 的系数,不影响自变量x的变化.
由周期函数得定义可知,的周期为.
新知形成
解:
【例1】求下列函数的周期:
⑴, ⑵;
⑶.
⑵令,得, 则.
分析:对于⑵,应从余弦函数的周期性出发,通过代数变形得出.
由的周期为,得
于是
所以
由周期函数得定义可知,的周期为.
新知形成
解:
【例1】求下列函数的周期:
⑴, ⑵;
⑶.
⑶令,得, 则.
分析:对于⑶,应从正弦函数的周期性出发,通过代数变形得出
.
由的周期为,得
于是
所以
由周期函数得定义可知,的周期为.
新知形成
回归例1得解题过程,你能发现函数周期与函数解析式中的哪些有关吗?
函数的周期与解析式中只与系数有关.
对于函数的最小正周期.
设,有
即
=
的最小正周期.
函数或的周期都为.
新知探求
思考:观察正弦曲线和余弦曲线,看它们是否关于原点或y轴对称?能否由此判定它们的奇偶性 ?如何证明?
正弦曲线关于原点O 对称 ,正弦函数y=sinx,x∈R为奇函数 ;余弦曲线关于 y 轴对称,余弦函数y=cos x,x∈R为偶函数.
新知探求
正弦曲线关于原点O 对称 ,正弦函数y=sinx,x∈R为奇函数 ;余弦曲线关于 y 轴对称,余弦函数y=cos x,x∈R为偶函数.
证明:
正余弦函数的奇偶性
正弦函数是奇函数,余弦函数是偶函数.
新知探求
除坐标原点外,正弦函数图像是否还有其它对称中心,它们的位置特征是什么?
正弦函数图像关于点(成对称中心,均为函数图像与交点,任意两个对称中心横坐标相差.
=
=图像关于点(成对称中心.
新知探求
正弦函数图像是否为轴对称图形 对称轴是否唯一?它们的位置特征是什么?
正弦函数图像关于直线成轴对称,每条对称轴经过图像最高或最低点,任意两条对称轴之间相差.
又
=图像关于直线成轴对称.
新知探求
类比正弦函数,请你根据余弦函数图像分析余弦函数对称轴、对称中心.
余弦函数图像关于直线成轴对称,每条对称轴经过图像最高或最低点,任意两条对称轴之间相差.
余弦函数图像关于点(成对称中心,均为函数图像与交点,任意两个对称中心横坐标相差.
知道一个函数具有周期性和奇偶性,对研究它的图象和性质有什么帮助?
新知探求
【例2】判断下列函数的奇偶性:
⑴, ⑵;
⑶; ⑷
解:
⑴∵函数的定义域不关于原点对称,
∴此函数既不是奇函数,也不是偶函数.
⑵∵函数的定义域R关于原点对称,
又
而
∴此函数是奇函数.
新知探求
【例2】判断下列函数的奇偶性:
⑶; ⑷
解:
⑶∵函数的定义域为,关于原点对称.
⑷由得,即得此函数定义域为,关于原点对称.
又
而
∴此函数是奇函数.
∴此函数是偶函数.
又
而
初试身手
1.函数的最小正周期为( )
A. B. C. D.
2.函数的周期是 .
解:
1.对则函数的最小正周期为,故选C.
2.函数的周期.
C
初试身手
3.判断下列函数的奇偶性:
⑴; ⑵; ⑶.
解:
⑴此函数为非奇非偶函数.
⑵此函数为偶函数.
⑶此函数的定义域为,它关于原点对称.
又
而
则此函数为奇函数.
初试身手
4.下列函数中是奇函数,且最小正周期为的函数是( )
A. B. C. D.
5.函数是奇函数,且对,都有,又,则
= .
解:
4.4.函数 , 都为偶函数;又也为偶函数;对,它为奇函数,周期,故选D.
5.由已知得,对,
则得周期为.
则.
D
又因为为奇函数,
-1
课堂小结
1.求函数的最小正周期的常用方法:
2.判断函数的奇偶性,必须坚持“定义域优先”的原则,准确求函数定义域和将式子合理变形是解决此类问题的关键.如果定义域关于原点对称,再看f(-x)与f(x)的关系,从而判断奇偶性.
(1)定义法,即观察出周期,再用定义来验证;也可由函数所具有的某些性质推出使f(x+T)=f(x)成立的T.
(2)图象法,即作出y=f(x)的图象,观察图象可求出T,如y=|sin x|.
(3)结论法,函数y=Asin(ωx+φ)(其中A,ω,φ为常数,A≠0,ω>0,x∈R)的周期.
作业布置
作业:P203练习 第3,4题 P213 习题5.4 第2,3题.
补充:
1.(多选题)下列关于x的函数f(x)=sin(x+φ)的说法正确的是( )
A.对任意的φ,f(x)都是非奇非偶函数 B.存在φ,使f(x)是偶函数
C.存在φ,使f(x)是奇函数 D.对任意的φ,f(x)都不是偶函数
2.已知,则= .
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
