华师大版九年级上册 第5章 杠杆专题练习(含解析)
文档属性
| 名称 | 华师大版九年级上册 第5章 杠杆专题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 358.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-12-15 17:30:08 | ||
图片预览



文档简介
杠杆专项练习
一、单选题
1.现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b,将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La,如图所示。取下铝条a后,将铝条b按上述操作方法使铁条AB再次水平平衡.此时OB的距离为Lx。下列判断正确的是( )
A.若LaB.若La成立
C.若LbD.若Lb2.某游客来栎社国际机场乘机,他所用的拉杆旅行箱示意图如图所示。装有物品的旅行箱整体可视为杠杆,O为支点,B为重心,A为拉杆的端点。在A点沿图示方向施加拉力F使旅行箱保持静止。下列说法正确的是( )
A.旅行箱受到的重力与水平地面对它的支持力是一对平衡力
B.其他条件不变时,仅缩短拉杆的长度, 拉力F减小
C.其他条件不变时,使拉力F的方向沿顺时针改变10°,拉力F增大
D.箱内物体下滑,重心位置由B变至B',拉力F增大
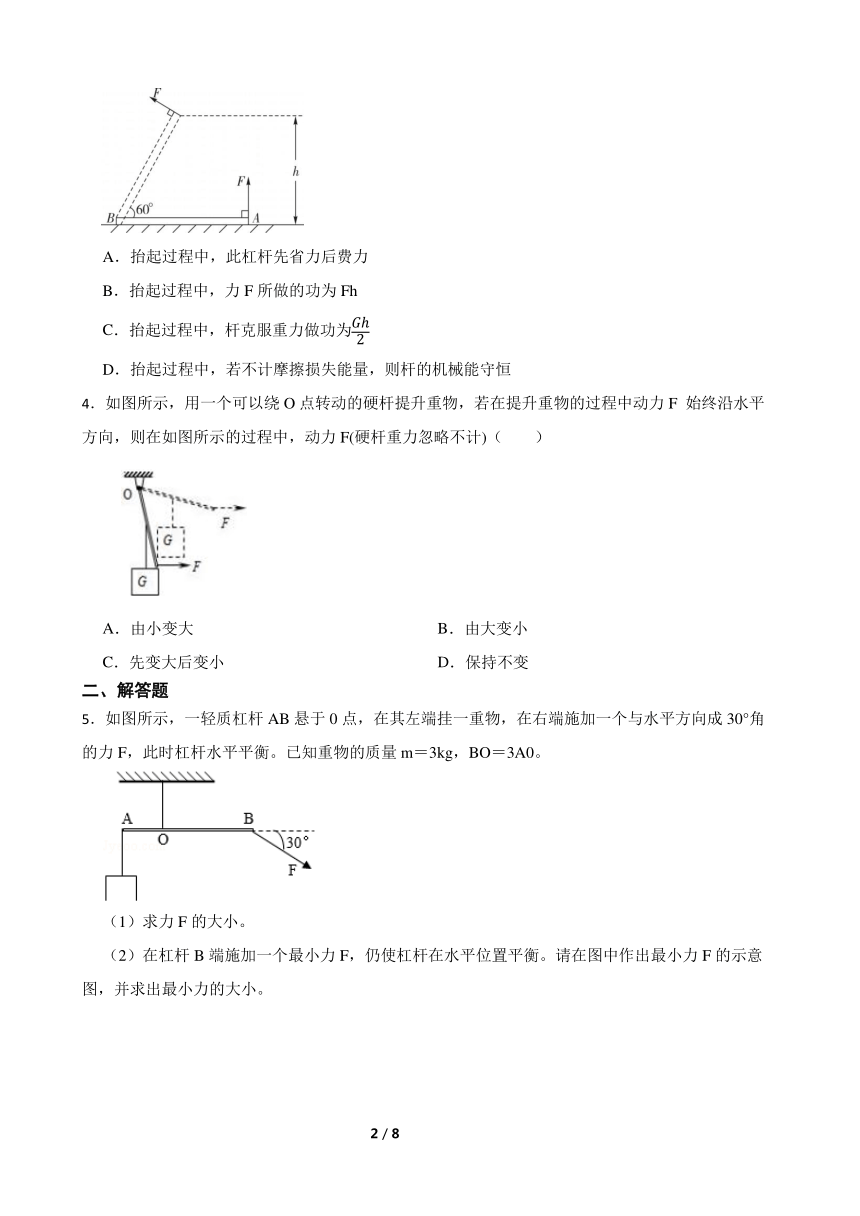
3.质量分布均匀、重为G的直杆AB置于水平面上(忽略杆的直径大小),小科同学现在A端施加外力F,匀速缓慢抬起直杆至如图位置(杆与水平面成60角),此时杆A端距地面高度为h,杆的B端始终和地面之间保持相对静止,F的方向始终和直杆垂直,则下列说法中正确的是( )
A.抬起过程中,此杠杆先省力后费力
B.抬起过程中,力F所做的功为Fh
C.抬起过程中,杆克服重力做功为
D.抬起过程中,若不计摩擦损失能量,则杆的机械能守恒
4.如图所示,用一个可以绕O点转动的硬杆提升重物,若在提升重物的过程中动力F 始终沿水平方向,则在如图所示的过程中,动力F(硬杆重力忽略不计)( )
A.由小变大 B.由大变小
C.先变大后变小 D.保持不变
二、解答题
5.如图所示,一轻质杠杆AB悬于0点,在其左端挂一重物,在右端施加一个与水平方向成30°角的力F,此时杠杆水平平衡。已知重物的质量m=3kg,BO=3A0。
(1)求力F的大小。
(2)在杠杆B端施加一个最小力F,仍使杠杆在水平位置平衡。请在图中作出最小力F的示意图,并求出最小力的大小。
6.在实际生活中,人们在抬较重的物体时,常用如图所示的三人共抬法。杠杆AB和CD质量不计,AB的中点为P,轻绳连接PC,在杠杆CD上的Q点连接轻绳悬挂重物,三人分别在A、B、D处抬杠杆。已知所抬物体重力为1200N,两根杠杆均处于水平位置静止,轻绳均竖直,AP=BP=DQ=2m,CQ=1m,分别计算A、D两处人对杠杆竖直向上的作用力FA和FD的大小。
7.如图所示,质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一边长为0.2m的质量均匀的正方体物块M,板的A端用一根与水平地面成30°夹角的细绳拉住,当绳的拉力F为80N时,物块M对地面的压强为5000Pa。求:
(1)在图上作出绳子对木板拉力的力臂L1。
(2)力臂L1为 m。
(3)物块M对地面的压力和物块M的重力各为多少?
8.如图是脚踏式翻盖垃圾桶,桶盖EDCO2的质量为500g,分布均匀、厚度不计,D为重心。脚踏杆和其它连接杆的质量均不计,桶盖闭合时,连接杆BC处于竖直状态。当脚踩A时,脚踏杆AB带动连接杆BC运动,打开桶盖。已知AO1=35 cm,BO1=20 cm,CO2=5 cm,CE=60 cm,请完成:
(1)在图中画出杠杆EDCO2的动力F1;
(2)若要把桶盖翻开,动力F1= N;
(3)若要把桶盖翻开,请计算脚对踏板A处的压力至少为多大?
答案解析部分
1.【答案】A
【解析】【分析】首先把原铁条和铝条a看做整体,原来水平平衡时整体的重心位于原支点处。
(1)当铝块变长时,将变长部分看成一个增加的物体,然后确定新支点,根据杠杆的平衡条件得出支点移动的方向,从而得出答案;
(2)当铝块变短时,将变短部分看做一个减少的物体,然后确定新支点,根据杠杆的平衡条件得出支点移动的方向,从而得出答案。【解答】由题意可知,将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La,
(1)如下图所示,若La<Lb<L,用铝条b替换铝条a就相当于在铝条a左侧放了一段长为Lb-La、重为Gb-Ga的铝条,
这一段铝条的重心距B端的长度为,
而铁条AB和铝条a组成的整体的重心在支架原来的位置,距B端的长度为La,
要使铁条AB水平平衡,由杠杆的平衡条件F1L1=F2L2可知,支架O应移到上述两个重心之间,
即,故A正确、B错误;
(2)如下图所示,若Lb<La,用铝条b替换铝条a就相当于从铝条a左侧截掉一段长为La-Lb、重为Ga-Gb的铝条,
也相当于距B端处施加一个竖直向上的力,其大小等于Ga-Gb,
由杠杆的平衡条件F1L1=F2L2可知,要使铁条AB水平平衡,支架O应向A端移动,则Lx>La,故C错误;
由Lb<La可知,,故D错误。
故选A。
2.【答案】C
【解析】【分析】对旅行箱受力分析,判定其受力情况,然后根据杠杆的平衡条件分析即可。【解答】A.在A点沿图示方向施加拉力F使旅行箱保持静止,旅行箱受到的合力为0,旅行箱受到竖直向下的重力、竖直向上的地面施加的支持力、斜向上的拉力F的共同作用,所以重力和支持力的大小不同,不是一对平衡力,故A错误;
B.由图知,O为支点,反向延长力F的作用线,由O点做F作用线的垂线,垂线段长为其力臂L,如图所示:
;
其它条件不变时,仅缩短拉杆的长度,由图可知,动力臂会变小。在阻力、阻力臂不变时,动力臂变小,根据杠杆的平衡条件“动力×动力臂=阻力×阻力臂”可知,拉力F增大,故B错误;
C.其它条件不变时,使拉力F的方向沿顺时针改变10°,动力臂会变小,在阻力、阻力臂不变时,动力臂变小,根据杠杆的平衡条件可知,拉力F增大,故C正确;
D.箱内物体下滑,重心位置由B变至B′,阻力不变,阻力臂变小,动力臂不变,根据杠杆的平衡条件可知,拉力F减小,故D错误。
故选C。
3.【答案】C
【解析】【分析】(1)分析动力臂和阻力臂的变化,从而确定省力或费力;
(2)(3)抬起的过程中,力F做的功等于克服重力做的功;
(4)机械能=动能+重力势能。
【解答】A.根据图片可知,B点为支点,杆的重力相当于阻力,F为动力。在抬起的过程中,阻力臂不断减小,而动力臂保持不变。根据杠杆的平衡条件F1L1=F2L2可知,越来越省力,故A错误;
BC.在抬起的过程中,力F做的功等于克服杠杆重力做的功。由于杆的重心升高,所以力F做的功为:W=Gh'=,故B错误,C正确;
D.在抬起的过程中,杆的高度不断增大,则它的重力势能不断增大。速度不变,则动能不变。根据”机械能=动能+重力势能“可知,杆的机械能增大,故D错误。
故选C。
4.【答案】A
【解析】【分析】根据杠杆的平衡条件F1L1=F2L2分析判断。
【解答】根据图片可知,在重物升高的过程中,阻力臂逐渐变大,而动力臂逐渐减小,根据F1L1=F2L2可知,动力F逐渐变大,故A正确,而B、C、D错误。
故选A。
5.【答案】(1)解:反向延长力F的作用线,过支点O作力F作用线的垂线即为F的力臂L1,因为右端施加一个与水平方向成30°的力F,则由1几何知识可知L1=2BO;
已知BO=3AO,重物质量m=3kg,则物体重力G=mg=3kg×10N/kg=30N;
由杠枉平衡条件得:G×L2=F×L1,即G×OA= ,
代入数据可得,30N×OA= ;解得F=20N.
(2)解:根据杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂最大,动力最小,在杠杆B端施加一个力,当OB为动力臂时,动力臂是最大的,根据杠杆的图平衡条件可知,此时的动力是最小的,最小动力垂直于OB向下,如图所示:
由杠杆平衡条件得:G×L2=F最小×L最大,代入数据可得,30N×OA=F最小×30A,解得F=10N。
【解析】【分析】(1)在直角三角形中,30°角所对的直角边等于斜边的一半,据此计算出动力臂L1,然后根据杠杆的平衡条件F1L1=F2L2列出方程,计算出拉力F的大小即可。
(2)在一个杠杆上,当以支点到力的作用点之间的线段为动力臂时最长,此时动力最小,据此完成作图,并根据杠杆的平衡条件F1L1=F2L2计算即可。
6.【答案】对杠杆CD,静止时可将C点作为支点,
根据杠杆平衡条件F1L1=F2L2得,FD×LCD=G×LCQ
FD×(2m+1m)=1200N×1m,FD=400N
以D为支点则有:FC×LCD=G×LDQ,FC×(2m+1m)=1200N×2m,FC=800N(或FC=G-FD =1200N-400N=800N)
对杠杆AB,静止时可将B作为支点,
根据杠杆平衡条件F1L1=F2L2得,FA×LAB= FC×LBP
FA×(2m+2m)=800N×2m,FA=400N
【解析】【分析】对杠杆CD,静止时可将C点作为支点,根据杠杆平衡条件F1L1=F2L2计算出D点的支持力,再以D点为支点,利用同样的方法计算出C点的支持力。
对于杠杆AB来说,可将B点看作支点,再根据杠杆的平衡条件F1L1=F2L2列式计算A点的支持力即可。
7.【答案】(1)
(2)0.6
(3)根据p= 可知,物块M对地面的压力为:F=pS=5000Pa×(0.2m×0.2m)=200N;
由于物体间力的作用是相互的,地面对M的支持力大小为F'=200N;
当绳的拉力F为80N时,根据杠杆的平衡条件可知:F1L1=FBLB,即:80N×0.6m=FB×0.4m,解得:FB=120N;
物体M处于静止状态,受到竖直向下的重力、竖直向上的B端绳子的拉力、竖直向上的地面的支持力的作用;则重力为:G=FB+F'=120N+200N=320N
【解析】【分析】(1)力臂是从杠杆的支点到力的作用线的垂直距离;
(2)根据直角三角形中30°角所对直角边的计算方法解答;
(3)首先根据正方形的面积S=a2计算出物块的底面积,再根据F=pS计算物体M对地面的压力。然后根据相互作用力的特点计算地面对M的支持力。当绳的拉力F为80N时,根据杠杆的平衡条件计算出作用在B端绳子上的拉力 FB ,最后根据二力平衡的知识 G=FB+F' 计算物体M的重力。
【解答】(1)通过支点O作细绳对杠杆的A端拉力的作用线的垂线,从支点O到垂足之间的距离就是力臂L1;
(2)根据图片可知,△AON为直角三角形,∠NAO=30°,则力臂L1=OA=×(1.6m-0.4m)=0.6m。
8.【答案】(1)
(2)35
(3)根据杠杆平衡条件可得
F×AO2=F2×O2B
F=20 N
【解析】【分析】(1)分析垃圾桶的工作过程,判断动力F1的三要素即可;
(2)根据杠杆的平衡条件F1L1=F2L2计算即可;
(3)对杠杆AO1B进行分析,再根据杠杆的平衡条件F1L1=F2L2计算即可。
【解答】(1)根据图片可知,对于杠杆 EDCO2 来说,垃圾桶的重力为阻力,方向竖直向下,则动力F1作用在C点,方向竖直向上,如下图所示:
。
(2)对于杠杆 EDCO2 来说,阻力为G=mg=0.5kg×10N/kg=5N,阻力臂为35cm,动力臂为5cm,
根据杠杆的平衡条件F1L1=F2L2得到:5N×35cm=F1×5cm;
解得:F1=35N。
(3)对于杠杆AO1B来说,阻力臂为O1B,动力臂为AO1,
根据杠杆的平衡条件F1L1=F2L2得到:F×35cm=35N×20cm;
解得:F=20N。
1 / 1
一、单选题
1.现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b,将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La,如图所示。取下铝条a后,将铝条b按上述操作方法使铁条AB再次水平平衡.此时OB的距离为Lx。下列判断正确的是( )
A.若La
C.若Lb
A.旅行箱受到的重力与水平地面对它的支持力是一对平衡力
B.其他条件不变时,仅缩短拉杆的长度, 拉力F减小
C.其他条件不变时,使拉力F的方向沿顺时针改变10°,拉力F增大
D.箱内物体下滑,重心位置由B变至B',拉力F增大
3.质量分布均匀、重为G的直杆AB置于水平面上(忽略杆的直径大小),小科同学现在A端施加外力F,匀速缓慢抬起直杆至如图位置(杆与水平面成60角),此时杆A端距地面高度为h,杆的B端始终和地面之间保持相对静止,F的方向始终和直杆垂直,则下列说法中正确的是( )
A.抬起过程中,此杠杆先省力后费力
B.抬起过程中,力F所做的功为Fh
C.抬起过程中,杆克服重力做功为
D.抬起过程中,若不计摩擦损失能量,则杆的机械能守恒
4.如图所示,用一个可以绕O点转动的硬杆提升重物,若在提升重物的过程中动力F 始终沿水平方向,则在如图所示的过程中,动力F(硬杆重力忽略不计)( )
A.由小变大 B.由大变小
C.先变大后变小 D.保持不变
二、解答题
5.如图所示,一轻质杠杆AB悬于0点,在其左端挂一重物,在右端施加一个与水平方向成30°角的力F,此时杠杆水平平衡。已知重物的质量m=3kg,BO=3A0。
(1)求力F的大小。
(2)在杠杆B端施加一个最小力F,仍使杠杆在水平位置平衡。请在图中作出最小力F的示意图,并求出最小力的大小。
6.在实际生活中,人们在抬较重的物体时,常用如图所示的三人共抬法。杠杆AB和CD质量不计,AB的中点为P,轻绳连接PC,在杠杆CD上的Q点连接轻绳悬挂重物,三人分别在A、B、D处抬杠杆。已知所抬物体重力为1200N,两根杠杆均处于水平位置静止,轻绳均竖直,AP=BP=DQ=2m,CQ=1m,分别计算A、D两处人对杠杆竖直向上的作用力FA和FD的大小。
7.如图所示,质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一边长为0.2m的质量均匀的正方体物块M,板的A端用一根与水平地面成30°夹角的细绳拉住,当绳的拉力F为80N时,物块M对地面的压强为5000Pa。求:
(1)在图上作出绳子对木板拉力的力臂L1。
(2)力臂L1为 m。
(3)物块M对地面的压力和物块M的重力各为多少?
8.如图是脚踏式翻盖垃圾桶,桶盖EDCO2的质量为500g,分布均匀、厚度不计,D为重心。脚踏杆和其它连接杆的质量均不计,桶盖闭合时,连接杆BC处于竖直状态。当脚踩A时,脚踏杆AB带动连接杆BC运动,打开桶盖。已知AO1=35 cm,BO1=20 cm,CO2=5 cm,CE=60 cm,请完成:
(1)在图中画出杠杆EDCO2的动力F1;
(2)若要把桶盖翻开,动力F1= N;
(3)若要把桶盖翻开,请计算脚对踏板A处的压力至少为多大?
答案解析部分
1.【答案】A
【解析】【分析】首先把原铁条和铝条a看做整体,原来水平平衡时整体的重心位于原支点处。
(1)当铝块变长时,将变长部分看成一个增加的物体,然后确定新支点,根据杠杆的平衡条件得出支点移动的方向,从而得出答案;
(2)当铝块变短时,将变短部分看做一个减少的物体,然后确定新支点,根据杠杆的平衡条件得出支点移动的方向,从而得出答案。【解答】由题意可知,将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La,
(1)如下图所示,若La<Lb<L,用铝条b替换铝条a就相当于在铝条a左侧放了一段长为Lb-La、重为Gb-Ga的铝条,
这一段铝条的重心距B端的长度为,
而铁条AB和铝条a组成的整体的重心在支架原来的位置,距B端的长度为La,
要使铁条AB水平平衡,由杠杆的平衡条件F1L1=F2L2可知,支架O应移到上述两个重心之间,
即,故A正确、B错误;
(2)如下图所示,若Lb<La,用铝条b替换铝条a就相当于从铝条a左侧截掉一段长为La-Lb、重为Ga-Gb的铝条,
也相当于距B端处施加一个竖直向上的力,其大小等于Ga-Gb,
由杠杆的平衡条件F1L1=F2L2可知,要使铁条AB水平平衡,支架O应向A端移动,则Lx>La,故C错误;
由Lb<La可知,,故D错误。
故选A。
2.【答案】C
【解析】【分析】对旅行箱受力分析,判定其受力情况,然后根据杠杆的平衡条件分析即可。【解答】A.在A点沿图示方向施加拉力F使旅行箱保持静止,旅行箱受到的合力为0,旅行箱受到竖直向下的重力、竖直向上的地面施加的支持力、斜向上的拉力F的共同作用,所以重力和支持力的大小不同,不是一对平衡力,故A错误;
B.由图知,O为支点,反向延长力F的作用线,由O点做F作用线的垂线,垂线段长为其力臂L,如图所示:
;
其它条件不变时,仅缩短拉杆的长度,由图可知,动力臂会变小。在阻力、阻力臂不变时,动力臂变小,根据杠杆的平衡条件“动力×动力臂=阻力×阻力臂”可知,拉力F增大,故B错误;
C.其它条件不变时,使拉力F的方向沿顺时针改变10°,动力臂会变小,在阻力、阻力臂不变时,动力臂变小,根据杠杆的平衡条件可知,拉力F增大,故C正确;
D.箱内物体下滑,重心位置由B变至B′,阻力不变,阻力臂变小,动力臂不变,根据杠杆的平衡条件可知,拉力F减小,故D错误。
故选C。
3.【答案】C
【解析】【分析】(1)分析动力臂和阻力臂的变化,从而确定省力或费力;
(2)(3)抬起的过程中,力F做的功等于克服重力做的功;
(4)机械能=动能+重力势能。
【解答】A.根据图片可知,B点为支点,杆的重力相当于阻力,F为动力。在抬起的过程中,阻力臂不断减小,而动力臂保持不变。根据杠杆的平衡条件F1L1=F2L2可知,越来越省力,故A错误;
BC.在抬起的过程中,力F做的功等于克服杠杆重力做的功。由于杆的重心升高,所以力F做的功为:W=Gh'=,故B错误,C正确;
D.在抬起的过程中,杆的高度不断增大,则它的重力势能不断增大。速度不变,则动能不变。根据”机械能=动能+重力势能“可知,杆的机械能增大,故D错误。
故选C。
4.【答案】A
【解析】【分析】根据杠杆的平衡条件F1L1=F2L2分析判断。
【解答】根据图片可知,在重物升高的过程中,阻力臂逐渐变大,而动力臂逐渐减小,根据F1L1=F2L2可知,动力F逐渐变大,故A正确,而B、C、D错误。
故选A。
5.【答案】(1)解:反向延长力F的作用线,过支点O作力F作用线的垂线即为F的力臂L1,因为右端施加一个与水平方向成30°的力F,则由1几何知识可知L1=2BO;
已知BO=3AO,重物质量m=3kg,则物体重力G=mg=3kg×10N/kg=30N;
由杠枉平衡条件得:G×L2=F×L1,即G×OA= ,
代入数据可得,30N×OA= ;解得F=20N.
(2)解:根据杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂最大,动力最小,在杠杆B端施加一个力,当OB为动力臂时,动力臂是最大的,根据杠杆的图平衡条件可知,此时的动力是最小的,最小动力垂直于OB向下,如图所示:
由杠杆平衡条件得:G×L2=F最小×L最大,代入数据可得,30N×OA=F最小×30A,解得F=10N。
【解析】【分析】(1)在直角三角形中,30°角所对的直角边等于斜边的一半,据此计算出动力臂L1,然后根据杠杆的平衡条件F1L1=F2L2列出方程,计算出拉力F的大小即可。
(2)在一个杠杆上,当以支点到力的作用点之间的线段为动力臂时最长,此时动力最小,据此完成作图,并根据杠杆的平衡条件F1L1=F2L2计算即可。
6.【答案】对杠杆CD,静止时可将C点作为支点,
根据杠杆平衡条件F1L1=F2L2得,FD×LCD=G×LCQ
FD×(2m+1m)=1200N×1m,FD=400N
以D为支点则有:FC×LCD=G×LDQ,FC×(2m+1m)=1200N×2m,FC=800N(或FC=G-FD =1200N-400N=800N)
对杠杆AB,静止时可将B作为支点,
根据杠杆平衡条件F1L1=F2L2得,FA×LAB= FC×LBP
FA×(2m+2m)=800N×2m,FA=400N
【解析】【分析】对杠杆CD,静止时可将C点作为支点,根据杠杆平衡条件F1L1=F2L2计算出D点的支持力,再以D点为支点,利用同样的方法计算出C点的支持力。
对于杠杆AB来说,可将B点看作支点,再根据杠杆的平衡条件F1L1=F2L2列式计算A点的支持力即可。
7.【答案】(1)
(2)0.6
(3)根据p= 可知,物块M对地面的压力为:F=pS=5000Pa×(0.2m×0.2m)=200N;
由于物体间力的作用是相互的,地面对M的支持力大小为F'=200N;
当绳的拉力F为80N时,根据杠杆的平衡条件可知:F1L1=FBLB,即:80N×0.6m=FB×0.4m,解得:FB=120N;
物体M处于静止状态,受到竖直向下的重力、竖直向上的B端绳子的拉力、竖直向上的地面的支持力的作用;则重力为:G=FB+F'=120N+200N=320N
【解析】【分析】(1)力臂是从杠杆的支点到力的作用线的垂直距离;
(2)根据直角三角形中30°角所对直角边的计算方法解答;
(3)首先根据正方形的面积S=a2计算出物块的底面积,再根据F=pS计算物体M对地面的压力。然后根据相互作用力的特点计算地面对M的支持力。当绳的拉力F为80N时,根据杠杆的平衡条件计算出作用在B端绳子上的拉力 FB ,最后根据二力平衡的知识 G=FB+F' 计算物体M的重力。
【解答】(1)通过支点O作细绳对杠杆的A端拉力的作用线的垂线,从支点O到垂足之间的距离就是力臂L1;
(2)根据图片可知,△AON为直角三角形,∠NAO=30°,则力臂L1=OA=×(1.6m-0.4m)=0.6m。
8.【答案】(1)
(2)35
(3)根据杠杆平衡条件可得
F×AO2=F2×O2B
F=20 N
【解析】【分析】(1)分析垃圾桶的工作过程,判断动力F1的三要素即可;
(2)根据杠杆的平衡条件F1L1=F2L2计算即可;
(3)对杠杆AO1B进行分析,再根据杠杆的平衡条件F1L1=F2L2计算即可。
【解答】(1)根据图片可知,对于杠杆 EDCO2 来说,垃圾桶的重力为阻力,方向竖直向下,则动力F1作用在C点,方向竖直向上,如下图所示:
。
(2)对于杠杆 EDCO2 来说,阻力为G=mg=0.5kg×10N/kg=5N,阻力臂为35cm,动力臂为5cm,
根据杠杆的平衡条件F1L1=F2L2得到:5N×35cm=F1×5cm;
解得:F1=35N。
(3)对于杠杆AO1B来说,阻力臂为O1B,动力臂为AO1,
根据杠杆的平衡条件F1L1=F2L2得到:F×35cm=35N×20cm;
解得:F=20N。
1 / 1
