组合图形的面积一课一练(含答案)人教版五年级数学上册(含解析)
文档属性
| 名称 | 组合图形的面积一课一练(含答案)人教版五年级数学上册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 757.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 00:00:00 | ||
图片预览




文档简介
组合图形的面积 一课一练(含答案)
人教版 五年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.有一块如图所示的铁板,如果给这块铁板涂油漆(只涂一面),每平方米用油漆0.5kg,那么一共需要油漆( )kg。
2.如图,大正方形是由4个直角三角形和一个小正方形拼成的。每个直角三角形的直角边分别为2cm和3cm,大正方形的面积是( )cm2。
3.小敏用一张边长20厘米的正方形彩纸做手工,她先将彩纸连续对折了2次,打开后沿相邻两边中点的连线剪去一个角(如图)。剩下彩纸的面积是( )平方厘米。
4.如图是由6个小正方形组成的,已知三角形A的面积是2cm2,则三角形B的面积是( )cm2,空白部分的面积是( )cm2。
5.如图,在长方形ABCD中,AB=8厘米,AD=6厘米,三角形ACE的面积是12平方厘米,那么梯形ABED的面积是( )平方厘米。
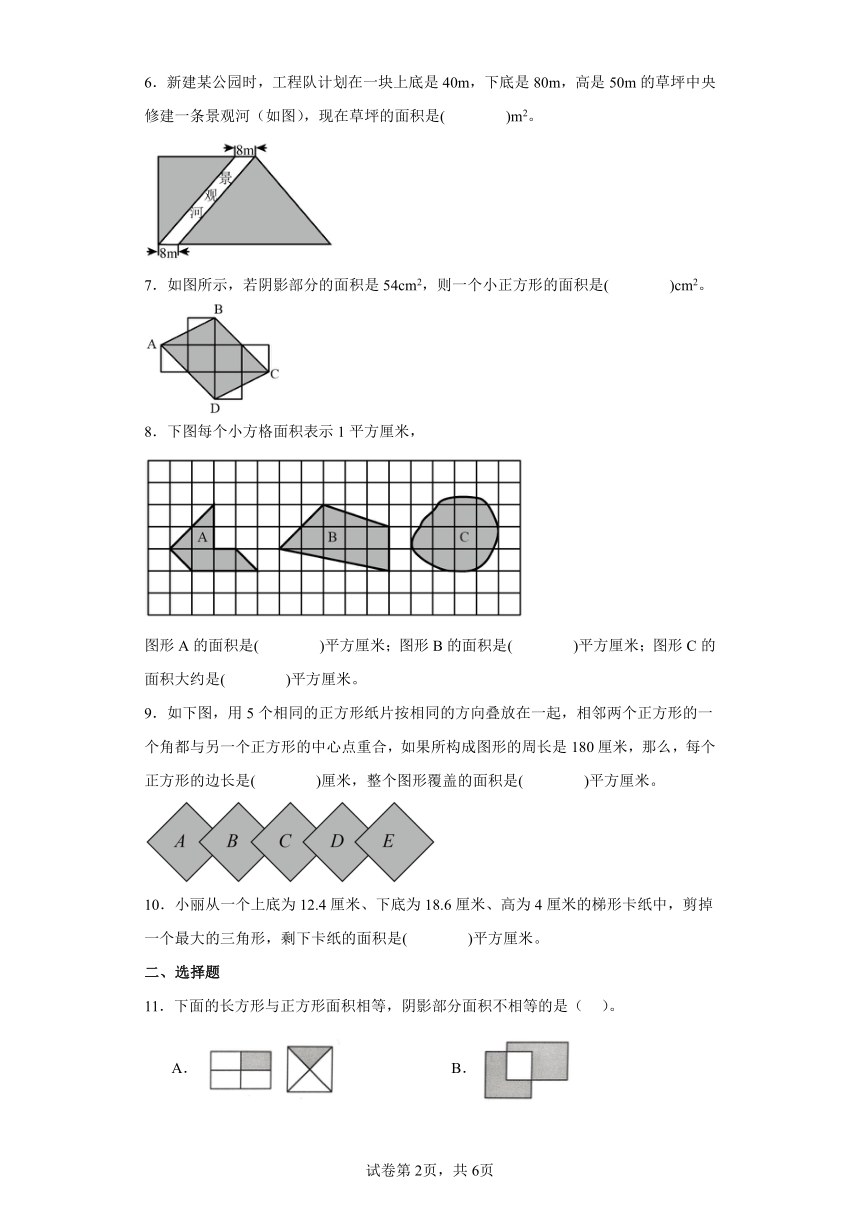
6.新建某公园时,工程队计划在一块上底是40m,下底是80m,高是50m的草坪中央修建一条景观河(如图),现在草坪的面积是( )m2。
7.如图所示,若阴影部分的面积是54cm2,则一个小正方形的面积是( )cm2。
8.下图每个小方格面积表示1平方厘米,
图形A的面积是( )平方厘米;图形B的面积是( )平方厘米;图形C的面积大约是( )平方厘米。
9.如下图,用5个相同的正方形纸片按相同的方向叠放在一起,相邻两个正方形的一个角都与另一个正方形的中心点重合,如果所构成图形的周长是180厘米,那么,每个正方形的边长是( )厘米,整个图形覆盖的面积是( )平方厘米。
10.小丽从一个上底为12.4厘米、下底为18.6厘米、高为4厘米的梯形卡纸中,剪掉一个最大的三角形,剩下卡纸的面积是( )平方厘米。
二、选择题
11.下面的长方形与正方形面积相等,阴影部分面积不相等的是( )。
A. B.
C. D.
12.如图所示,是两个大小相同的正方形,正方形中的阴影部分哪一个面积更大?( )
A.甲大 B.乙大 C.一样大 D.无法确定
13.如图平行四边形中有①②③三个三角形,关于这三个三角形面积间的关系,下面的说法正确的是( )。
A.①>②+③ B.①<②+③ C.①=②=③ D.①=②+③
14.列图形中,涂色部分面积与空白部分面积相等的是( )。
A. B.
C. D.
15.如图所示,每个小正方形的面积为1cm2,请你估计一下,这枚日脚印的面积约是( )cm2。
A.72 B.48 C.30 D.12
16.如图,四边形AECF中,4条线段的长度分别是AB=2cm,CE=6cm,CD=5cm, AF=4cm, 那么,图中阴影部分的面积是( )cm2。
A.17.5 B.16 C.14 D.条件不足,无法确定
17.图中每个小方格的面积是1cm ,下面是三种估算这片叶子的面积的方法,估算方法较合理的有( )种。
①将图案转化成底是4cm,高是9cm的三角形。
②用数格子的方法:大于半格的记1格,不够半格的记为0。
③方格纸上满格的有25格,都记1格,不满格的有20格,都记0。
A.1 B.2 C.3 D.0
三、判断题
18.如图,阴影甲的面积大于阴影乙的面积。( )
19.面积相等的图形,形状一定相同。( )
20.估算的面积一般比实际面积大。( )
21.不规则图形的面积可以转化为学过的图形来估算。( )
22.长方形、三角形、平行四边形、正六边形都可以单独密铺。( )
四、图形计算
23.计算下面图形中涂色部分的面积。(单位:厘米)
五、解答题
24.下图是一面广告牌,粉刷这面广告牌每平方分米需要0.15千克涂料,请问一共要用多少千克涂料?
25.学校新开辟了一片地用来做科学小农场,五年级3个班各自得到一片面积一样的土地,中间有两条宽0.5米,长6.6米的小路(形状是平行四边形),每个班分到了多少平方米的土地?
26.
(1)在上面的方格图中标出下列各点并依次连成封闭图形。
A(2,1);B(2,4);C(5,1)
填空:这是一个( )形。
(2)求出上面方格图中五边形的面积。(每个小方格的边长为1cm)
27.如下图是实验小学航模组同学设计的一枚火箭模型的平面图,你能算出它的面积吗?(单位:厘米)
28.建党100周年之际,某革命教育展览馆计划把原来的等腰梯形展区扩建成一个长方形展区(如图),求展区面积比原来增加了多少平方米?
29.如图,已知有一块四边形花圃ABCD,其中E,F分别为AB,AG上的点,且BE=2AE,G,H分别是DF,BC上的点,且BH=HC,FG=GD,连接EF,BF,BG,HD,将花圃分成五块,图中阴影部分种兰花,三角形AEF的面积是25平方米,三角形BFG的面积是150平方米,三角形HCD的面积是90平方米。空白部分种郁金香,那么郁金香的面积为多少平方米?
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.3.3
【分析】观察图形可知,该铁板的面积等于长方形的面积加上梯形的面积,再根据长方形的面积公式:S=ab,梯形的面积公式:S=(a+b)h÷2,据此求出铁板的面积,再用铁板的面积乘0.5即可求解。
【详解】2.8×1.5+(2.8+1.2)×1.2÷2
=4.2+4×1.2÷2
=4.2+2.4
=6.6(m2)
6.6×0.5=3.3(kg)
则那么一共需要油漆3.3kg。
【点睛】本题考查长方形和梯形的面积,熟记公式是解题的关键。
2.13
【分析】由图可知,小正方形的边长等于长直角边与短直角边的差,利用“正方形的面积=边长×边长”表示出小正方形的面积,利用“三角形的面积=底×高÷2”表示出4个直角三角形的面积,大正方形的面积=小正方形的面积+4个直角三角形的面积,据此解答。
【详解】(3-2)×(3-2)+3×2÷2×4
=1×1+3×2÷2×4
=1+6÷2×4
=1+3×4
=1+12
=13(cm2)
所以,大正方形的面积是13cm2。
【点睛】本题主要考查组合图形面积的计算,掌握正方形和三角形的面积计算公式是解答题目的关键。
3.350
【分析】根据图示可知,可以把这种彩纸分成8份,剩余彩纸是整个正方形面积的7份,利用正方形面积公式:S=a×a,计算即可。
【详解】如图:
20×20÷8×7
=400÷8×7
=50×7
=350(平方厘米)
剩下彩纸的面积是350平方厘米。
【点睛】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
4. 1 9
【分析】看图,三角形A的底是小正方形的边长,高是小正方形边长的2倍。三角形面积=底×高÷2,所以边长×2×边长÷2=三角形A的面积,所以边长×边长=2cm2,即一个小正方形的面积是2cm2。三角形B的底和高都是小正方形的边长,那么它的面积是小正方形的一半,用2cm2除以2,即可求出三角形B的面积。将小正方形面积乘6,即可求出整个图形的面积,再将其减去三角形A和B的面积,求出空白部分的面积。
【详解】2÷2=1(cm2)
2×6=12(cm2)
12―2―1=9(cm2)
所以,三角形B的面积是1cm2,空白部分的面积是9cm2。
【点睛】本题考查了三角形和组合图形的面积,灵活运用三角形的面积公式是解题关键。
5.60
【分析】先依据三角形的面积公式:S=ah÷2,用12×2÷6即可求出三角形ACE中CE的长度,也就等于知道了梯形的下底,进而依据梯形的面积公式:S=(a+b)×h÷2,代入数据即可求解。
【详解】12×2÷6=4(厘米)
(8+4+8)×6÷2
=20×6÷2
=60(平方厘米)
这个梯形的面积是60平方厘米。
【点睛】此题主要考查三角形和梯形的面积公式的灵活应用。
6.2600
【分析】从图中可知,景观河是一个底为8m,高为50m的平行四边形;则现在草坪的面积=梯形的面积-平行四边形的面积,根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,代入数据计算求解。
【详解】梯形的面积:
(40+80)×50÷2
=120×50÷2
=3000(m2)
平行四边形的面积:
8×50=400(m2)
草坪的面积:
3000-400=2600(m2)
现在草坪的面积是2600m2。
【点睛】本题考查梯形、平行四边形面积公式的运用,分析组合图形是由哪些基本图形组成,然后看是求几种图形的面积和还是求面积差,根据图形面积公式解答。
7.9
【分析】数一数涂色部分的面积一共是由6个小正方形组成的,所以用涂色部分的面积除以正方形的个数即可求出一个小正方形的面积。
【详解】54÷6=9(cm2)
即一个小正方形的面积是9cm2。
【点睛】此题的解题关键是通过转化的数学思想,把阴影部分的面积转化成正方形的面积。
8. 5 9 9
【分析】如图,图形A的面积=三角形面积+平行四边形面积;图形B的面积=三角形面积+梯形面积+三角形面积;图形C的面积可以看作梯形进行计算。三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,据此分析。
【详解】2×2÷2+3×1
=2+3
=5(平方厘米)
4×1÷2+(4+5)×1÷2+5×1÷2
=2+9×1÷2+2.5
=2+4.5+2.5
=9(平方厘米)
(2+4)×3÷2
=6×3÷2
=9(平方厘米)
图形A的面积是5平方厘米;图形B的面积是9平方厘米;图形C的面积大约是9平方厘米。
【点睛】关键是掌握并灵活运用三角形、平行四边形和梯形面积公式。
9. 15 900
【分析】通过平移可知,这个图形的周长相当于3个正方形的周长,已知所构成图形的周长是180厘米,用180÷3即可求出一个正方形的周长,再根据正方形的周长公式,用一个正方形的周长除以4,即可求出正方形的边长;这个图形的面积相当于4个正方形的面积;根据正方形的面积公式,代入数据求出一个正方形的面积,再乘4即可求出结果。
【详解】180÷3=60(厘米)
60÷4=15(厘米)
15×15×4=900(平方厘米)
每个正方形的边长是15厘米,整个图形覆盖的面积是900平方厘米。
【点睛】本题可通过平移巧求正方形的边长,掌握相关公式是解答本题的关键。
10.24.8
【分析】要想在这个梯形卡纸中剪去一个最大的三角形,必须把梯形的下底作为三角形的底。把梯形的高作为三角形的高,则剩下的图形的面积就是以梯形的上底为底,梯形的高为高的三角形的面积,据此利用三角形的面积公式计算即可解答。
【详解】12.4×4÷2=24.8(平方厘米)
即剩下卡纸的面积是24.8平方厘米。
【点睛】此题考查组合图形的面积,解决此题关键是弄明白怎么剪才能使三角形的面积最大,进而得出剩下的是以上底为底边的三角形的面积。
11.C
【分析】从图中可知,阴影部分的面积=长方形(或正方形)的面积-空白部分的面积,已知长方形与正方形的面积相等,如果空白部分的面积不相等,那么阴影部分的面积就不相等。
【详解】A.因为长方形与正方形的面积相等,阴影部分分别占长方形、正方形的,所以阴影部分面积相等;
B.因为长方形与正方形的面积相等,空白部分的面积也相等,所以阴影部分面积相等;
C.因为长方形的空白部分比正方形的空白部分大,所以阴影部分的面积不相等;
D.因为长方形与正方形的面积相等,空白部分的面积也相等,所以阴影部分面积相等。
故答案为:C
【点睛】本题考查组合图形面积的求法,关键是分析出阴影部分的面积是由哪些图形面积相减得到,再看这些图形面积是否相等,进而得出结论。
12.B
【分析】甲图的阴影部分是一个平行四边形,从图中可知,平行四边形的底小于正方形边长的一半,平行四边形的高等于正方形的边长;根据平行四边形的面积=底×高,正方形的面积=边长×边长,得出平行四边形的面积小于正方形面积的一半;
如下图,在乙图上画小方格,正方形共有32个小三角形,阴影部分有16个小三角形,所以乙图阴影部分的面积等于正方形面积的一半;
据此比较,得出结论。
【详解】甲图的阴影部分是一个平行四边形,平行四边形的面积小于正方形面积的一半;
乙图的阴影部分是4个小正方形,它们的面积之和等于正方形面积的一半。
因为两个正方形的面积相等,所以乙图阴影部分的面积>甲图阴影部分的面积。
综上所述,正方形中的阴影部分乙的面积更大。
故答案为:B
【点睛】本题考查组合图形面积的求法,把比较甲、乙两个图形阴影部分的面积转移到各图形阴影部分面积与正方形的面积相比较,进而得出结论。
13.D
【分析】如图:假设中间的三角形为④,平行四边形的高和对边相等,分别是h、a,则②+③+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的底乘高除以2;三角形①+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的下底乘高除以2,即可得解。
【详解】假设中间的三角形为④,平行四边形的高为h,底边长为a,
则②+③+④的面积=a×h÷2,①+④的面积=a×h÷2,
所以②+③+④=①+④,
即①=②+③。
故答案为:D
【点睛】此题关键是利用中间量,通过三角形的面积公式,从而解决问题。
14.A
【分析】根据三角形面积:,梯形面积:计算,继而比较大小即可。
【详解】A.涂色部分和空白部分是等底等高的三角形,面积相等。
B.涂色部分三角形和空白部分的梯形等高,梯形的上底+下底>三角形的底,故梯形的面积>三角形面积。
C.令梯形的高为h,则:
涂色三角形面积:
空白的两个三角形面积:
b+c>a
涂色三角形面积<空白三角形面积。
D.因梯形的上底小于下底,涂色和空白三角形等高。
则:涂色三角形面积大于空白三角形面积。
故答案为:A
【点睛】掌握三角形面积和梯形面积计算方法是解答的关键。
15.B
【分析】可以把这个脚掌看作一个长是12cm,宽是4cm的长方形,根据长方形的面积:长×宽,把数代入即可求解。
【详解】12×4=48(cm2)
如图所示,每个小正方形的面积为1cm2,请你估计一下,这枚日脚印的面积约是48cm2。
故答案为:B
【点睛】熟练掌握数格法求不规则图形的面积的方法是解答本题的关键。
16.B
【分析】连接AC,将四边形ABCD分割成△ADC与△ABC,△ADC的底是CD,高是AF,△ABC的底是AB,高是CE。△ADC的面积:5×4÷2=10(平方厘米);△ABC的面积: 2×6÷2=6(平方厘米);10+6=16(平方厘米),则四边形ABCD的面积是16平方厘米。
【详解】如图所示:
5×4÷2
=20÷2
=10(平方厘米)
2×6÷2
=12÷2
=6(平方厘米)
10+6=16(平方厘米)
则四边形ABCD的面积是16平方厘米。
故答案为:B
【点睛】本题考查三角形的面积,明确把阴影部分拆成两个三角形是解题的关键。
17.A
【分析】①可以把不规则图形看成近似于规则的图形估算面积。
②③用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
【详解】①,可以将图案转化成底是7cm,高是9cm的三角形,原方法错误。
②用数格子的方法:大于半格的记1格,不够半格的记为0,方法正确。
③方格纸上满格的有25格,都记1格,不满格的有20格,都记0,记0的太多,方法错误。
估算方法较合理的有1种。
故答案为:A
【点睛】关键是掌握不规则图形面积的估算方法。
18.×
【分析】先估算甲乙的面积各是多少,然后再进行比较,据此即可解答。
【详解】通过观察甲的面积相当于2个小方格面积,乙的面积相当于2个半方格的面积,所以乙的面积比甲大。
故答案为:错误
【点睛】本题考查学生对面积及面积的大小比较知识的掌握,解题的关键是对不规则图形面积的估算。
19.×
【详解】如果两个图形的面积相等,那么它们的形状不一定相同,所以本题说法错误;
故答案为:×
20.×
【分析】把不规则图形看成近似于规则的图形估算面积,有时候估算的面积比实际面积大,有时候估算的面积比实际面积小。
【详解】根据分析,估算的面积一般比实际面积大,说法错误。
故答案为:×
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
21.√
【分析】不规则图形面积的估算方法:可以借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
【详解】不规则图形的面积可以转化为学过的图形来估算,说法正确。
故答案为:√
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
22.√
【分析】多边形里面三角形的内角和是180°,180°的2倍是360°;正四边形的每个角是90°,90°的4倍是360°;正六边形的每个角是120°,120°的3倍是360°;因此多边形中有三角形、正四边形、正六边形可以密铺,正五边形不能密铺;长方形的每个角是90°,所以长方形可以密铺,平行四边形同一边的角和是180°,180°的2倍是360°,所以平行四边形也可以密铺;据此解答。
【详解】长方形、三角形、平行四边形、正六边形都可以单独密铺。原题干说法正确。
故答案为:√
【点睛】本题主要考查了密铺的知识,注意判断图形对应的角能否组成360°。
23.42平方厘米;26平方厘米
【分析】(1)涂色部分的面积=平行四边形的面积-三角形的面积。根据平行四边形的面积=底×高,用8×6求出平行四边形的面积(48平方厘米);三角形的底是8-3-2=3(厘米),根据三角形的面积=底×高÷2,用3×4÷2求出三角形的面积(6平方厘米);用48-6求出涂色部分的面积。
(2)如下图,涂色部分的面积=正方形ABCD的面积+正方形CEFG的面积-三角形ABD的面积-三角形BEF的面积。根据正方形的面积=边长×边长,用8×8求出正方形ABCD的面积(64平方厘米),用6×6求出正方形CEFG的面积(36平方厘米);根据三角形的面积=底×高÷2,用8×8÷2求出三角形ABD的面积(32平方厘米),用(8+6)×6÷2求出三角形BEF的面积(42平方厘米);最后用64+36-32-42求出涂色部分的面积。
【详解】8×6-(8-3-2)×4÷2
=48-3×4÷2
=48-12÷2
=48-6
=42(平方厘米)
涂色部分面积是42平方厘米。
8×8+6×6-8×8÷2-(8+6)×6÷2
=64+36-32-14×6÷2
=100-32-84÷2
=68-42
=26(平方厘米)
涂色部分面积是26平方厘米。
24.14.4千克
【分析】将数据代入三角形面积公式:S=ah÷2及平行四边形面积公式:S=ah,分别求出三角形与平行四边形的面积,求和即可求出这面广告牌的面积,最后用广告牌的面积乘每平方分米需要的涂料即可。
【详解】12×4÷2+12×6
=48÷2+72
=24+72
=96(平方分米)
96×0.15=14.4(千克)
答:一共要用14.4千克涂料。
【点睛】本题主要考查组合图形面积的求法,解题时通常将组合图形分割成基础图形,再求面积。
25.17.2平方米
【分析】根据题意,两条小路是两个底为0.5米,高为6米的平行四边形;从图中可知,空白部分的面积=长方形的面积-2个平行四边形的面积,根据长方形的面积=长×宽,平行四边形的面积=底×高,代入数据计算,求出空白部分的面积,也是五年级3个班的土地总面积;再用3个班的土地总面积除以3,即是平均每个班分到的面积。
【详解】(9.6×6-0.5×6×2)÷3
=(57.6-3×2)÷3
=(57.6-6)÷3
=51.6÷3
=17.2(平方米)
答:每个班分到了17.2平方米的土地。
【点睛】本题考查组合图形面积的求法,结合图形分析出组合图形的面积是由哪些图形的面积相加或相减得到,再根据图形的面积公式求解。
26.(1)图见详解;直角三角
(2)16.5平方厘米
【详解】(1)根据数对表示位置的方法,在方格图中标出下列各点并依次连成封闭图形,解答即可。
(2)方格图中五边形的面积等于上底是6厘米,下底是3厘米,高3厘米的梯形面积加底是6厘米,高1厘米的三角形面积,据此解答即可。
【解答】(1)在上面的方格图中标出下列各点并依次连成封闭图形。如图:
A(2,1);B(2,4);C(5,1)
这是一个直角三角形。
(2)(6+3)×3÷2+6×1÷2
=9×3÷2+6×1÷2
=13.5+3
=16.5(平方厘米)
所以五边形的面积是16.5平方厘米。
【点睛】此题考查数对位置和组合图形的面积。确定列数,一般从左往右;确定行数,一般从前往后或从下往上。用数对示位置时, 先说列,后说行。组合图形是由几个简单的图形组合而成的,其面积既可以看作几个简单图形的面积和,也可以看作几个简单图形的面积差。
27.696平方厘米
【分析】火箭模型的面积=上底是16厘米,下底是8厘米,高是8厘米的梯形面积+长是70厘米,宽是8厘米的长方形面积+底是8厘米,高是10厘米的三角形面积;根据梯形面积公式:面积=(上底+下底)×高÷2;长方形面积公式:面积=长×宽;三角形面积公式:面积=底×高÷2,代入数据,即解答。
【详解】(16+8)×8÷2+70×8+8×10÷2
=24×8÷2+560+80÷2
=192÷2+560+40
=96+560+40
=656+40
=696(平方厘米)
答:它的面积是696平方厘米。
28.425平方米
【分析】先根据长方形的面积=长×宽,用62×25求出长方形的面积;再根据梯形的面积=(上底+下底)×高÷2,用(28+62)×25÷2求出梯形的面积;最后用长方形的面积减去梯形的面积,即可求出展区面积比原来增加了多少平方米。
【详解】62×25-(28+62)×25÷2
=1550-90×25÷2
=1550-2250÷2
=1550-1125
=425(平方米)
答:展区面积比原来增加了425平方米。
29.440平方米
【分析】连接BD,如图所示:
三角形面积=底×高÷2,三角形AEF和三角形BEF高相等,并且BE=2AE,那么三角形BEF的面积是三角形AEF面积的2倍;
FG=GD,那么三角形BGD和三角形BFG等底等高,那么这两个三角形的面积相等;
同理,BH=HC,那么三角形BHD和三角形HCD等底等高,面积相等。
将空白部分的面积相加,求出种植郁金香的面积即可。
【详解】25×2=50(平方米)
50+150+150+90=440(平方米)
答:郁金香的面积是440平方米。
【点睛】本题考查了三角形的面积、组合图形的面积,熟记并灵活运用三角形的面积公式,并掌握割补法求组合图形的面积是解题的关键。
答案第1页,共2页
答案第1页,共2页
人教版 五年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.有一块如图所示的铁板,如果给这块铁板涂油漆(只涂一面),每平方米用油漆0.5kg,那么一共需要油漆( )kg。
2.如图,大正方形是由4个直角三角形和一个小正方形拼成的。每个直角三角形的直角边分别为2cm和3cm,大正方形的面积是( )cm2。
3.小敏用一张边长20厘米的正方形彩纸做手工,她先将彩纸连续对折了2次,打开后沿相邻两边中点的连线剪去一个角(如图)。剩下彩纸的面积是( )平方厘米。
4.如图是由6个小正方形组成的,已知三角形A的面积是2cm2,则三角形B的面积是( )cm2,空白部分的面积是( )cm2。
5.如图,在长方形ABCD中,AB=8厘米,AD=6厘米,三角形ACE的面积是12平方厘米,那么梯形ABED的面积是( )平方厘米。
6.新建某公园时,工程队计划在一块上底是40m,下底是80m,高是50m的草坪中央修建一条景观河(如图),现在草坪的面积是( )m2。
7.如图所示,若阴影部分的面积是54cm2,则一个小正方形的面积是( )cm2。
8.下图每个小方格面积表示1平方厘米,
图形A的面积是( )平方厘米;图形B的面积是( )平方厘米;图形C的面积大约是( )平方厘米。
9.如下图,用5个相同的正方形纸片按相同的方向叠放在一起,相邻两个正方形的一个角都与另一个正方形的中心点重合,如果所构成图形的周长是180厘米,那么,每个正方形的边长是( )厘米,整个图形覆盖的面积是( )平方厘米。
10.小丽从一个上底为12.4厘米、下底为18.6厘米、高为4厘米的梯形卡纸中,剪掉一个最大的三角形,剩下卡纸的面积是( )平方厘米。
二、选择题
11.下面的长方形与正方形面积相等,阴影部分面积不相等的是( )。
A. B.
C. D.
12.如图所示,是两个大小相同的正方形,正方形中的阴影部分哪一个面积更大?( )
A.甲大 B.乙大 C.一样大 D.无法确定
13.如图平行四边形中有①②③三个三角形,关于这三个三角形面积间的关系,下面的说法正确的是( )。
A.①>②+③ B.①<②+③ C.①=②=③ D.①=②+③
14.列图形中,涂色部分面积与空白部分面积相等的是( )。
A. B.
C. D.
15.如图所示,每个小正方形的面积为1cm2,请你估计一下,这枚日脚印的面积约是( )cm2。
A.72 B.48 C.30 D.12
16.如图,四边形AECF中,4条线段的长度分别是AB=2cm,CE=6cm,CD=5cm, AF=4cm, 那么,图中阴影部分的面积是( )cm2。
A.17.5 B.16 C.14 D.条件不足,无法确定
17.图中每个小方格的面积是1cm ,下面是三种估算这片叶子的面积的方法,估算方法较合理的有( )种。
①将图案转化成底是4cm,高是9cm的三角形。
②用数格子的方法:大于半格的记1格,不够半格的记为0。
③方格纸上满格的有25格,都记1格,不满格的有20格,都记0。
A.1 B.2 C.3 D.0
三、判断题
18.如图,阴影甲的面积大于阴影乙的面积。( )
19.面积相等的图形,形状一定相同。( )
20.估算的面积一般比实际面积大。( )
21.不规则图形的面积可以转化为学过的图形来估算。( )
22.长方形、三角形、平行四边形、正六边形都可以单独密铺。( )
四、图形计算
23.计算下面图形中涂色部分的面积。(单位:厘米)
五、解答题
24.下图是一面广告牌,粉刷这面广告牌每平方分米需要0.15千克涂料,请问一共要用多少千克涂料?
25.学校新开辟了一片地用来做科学小农场,五年级3个班各自得到一片面积一样的土地,中间有两条宽0.5米,长6.6米的小路(形状是平行四边形),每个班分到了多少平方米的土地?
26.
(1)在上面的方格图中标出下列各点并依次连成封闭图形。
A(2,1);B(2,4);C(5,1)
填空:这是一个( )形。
(2)求出上面方格图中五边形的面积。(每个小方格的边长为1cm)
27.如下图是实验小学航模组同学设计的一枚火箭模型的平面图,你能算出它的面积吗?(单位:厘米)
28.建党100周年之际,某革命教育展览馆计划把原来的等腰梯形展区扩建成一个长方形展区(如图),求展区面积比原来增加了多少平方米?
29.如图,已知有一块四边形花圃ABCD,其中E,F分别为AB,AG上的点,且BE=2AE,G,H分别是DF,BC上的点,且BH=HC,FG=GD,连接EF,BF,BG,HD,将花圃分成五块,图中阴影部分种兰花,三角形AEF的面积是25平方米,三角形BFG的面积是150平方米,三角形HCD的面积是90平方米。空白部分种郁金香,那么郁金香的面积为多少平方米?
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.3.3
【分析】观察图形可知,该铁板的面积等于长方形的面积加上梯形的面积,再根据长方形的面积公式:S=ab,梯形的面积公式:S=(a+b)h÷2,据此求出铁板的面积,再用铁板的面积乘0.5即可求解。
【详解】2.8×1.5+(2.8+1.2)×1.2÷2
=4.2+4×1.2÷2
=4.2+2.4
=6.6(m2)
6.6×0.5=3.3(kg)
则那么一共需要油漆3.3kg。
【点睛】本题考查长方形和梯形的面积,熟记公式是解题的关键。
2.13
【分析】由图可知,小正方形的边长等于长直角边与短直角边的差,利用“正方形的面积=边长×边长”表示出小正方形的面积,利用“三角形的面积=底×高÷2”表示出4个直角三角形的面积,大正方形的面积=小正方形的面积+4个直角三角形的面积,据此解答。
【详解】(3-2)×(3-2)+3×2÷2×4
=1×1+3×2÷2×4
=1+6÷2×4
=1+3×4
=1+12
=13(cm2)
所以,大正方形的面积是13cm2。
【点睛】本题主要考查组合图形面积的计算,掌握正方形和三角形的面积计算公式是解答题目的关键。
3.350
【分析】根据图示可知,可以把这种彩纸分成8份,剩余彩纸是整个正方形面积的7份,利用正方形面积公式:S=a×a,计算即可。
【详解】如图:
20×20÷8×7
=400÷8×7
=50×7
=350(平方厘米)
剩下彩纸的面积是350平方厘米。
【点睛】本题主要考查组合图形的面积,关键利用规则图形的面积公式计算。
4. 1 9
【分析】看图,三角形A的底是小正方形的边长,高是小正方形边长的2倍。三角形面积=底×高÷2,所以边长×2×边长÷2=三角形A的面积,所以边长×边长=2cm2,即一个小正方形的面积是2cm2。三角形B的底和高都是小正方形的边长,那么它的面积是小正方形的一半,用2cm2除以2,即可求出三角形B的面积。将小正方形面积乘6,即可求出整个图形的面积,再将其减去三角形A和B的面积,求出空白部分的面积。
【详解】2÷2=1(cm2)
2×6=12(cm2)
12―2―1=9(cm2)
所以,三角形B的面积是1cm2,空白部分的面积是9cm2。
【点睛】本题考查了三角形和组合图形的面积,灵活运用三角形的面积公式是解题关键。
5.60
【分析】先依据三角形的面积公式:S=ah÷2,用12×2÷6即可求出三角形ACE中CE的长度,也就等于知道了梯形的下底,进而依据梯形的面积公式:S=(a+b)×h÷2,代入数据即可求解。
【详解】12×2÷6=4(厘米)
(8+4+8)×6÷2
=20×6÷2
=60(平方厘米)
这个梯形的面积是60平方厘米。
【点睛】此题主要考查三角形和梯形的面积公式的灵活应用。
6.2600
【分析】从图中可知,景观河是一个底为8m,高为50m的平行四边形;则现在草坪的面积=梯形的面积-平行四边形的面积,根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,代入数据计算求解。
【详解】梯形的面积:
(40+80)×50÷2
=120×50÷2
=3000(m2)
平行四边形的面积:
8×50=400(m2)
草坪的面积:
3000-400=2600(m2)
现在草坪的面积是2600m2。
【点睛】本题考查梯形、平行四边形面积公式的运用,分析组合图形是由哪些基本图形组成,然后看是求几种图形的面积和还是求面积差,根据图形面积公式解答。
7.9
【分析】数一数涂色部分的面积一共是由6个小正方形组成的,所以用涂色部分的面积除以正方形的个数即可求出一个小正方形的面积。
【详解】54÷6=9(cm2)
即一个小正方形的面积是9cm2。
【点睛】此题的解题关键是通过转化的数学思想,把阴影部分的面积转化成正方形的面积。
8. 5 9 9
【分析】如图,图形A的面积=三角形面积+平行四边形面积;图形B的面积=三角形面积+梯形面积+三角形面积;图形C的面积可以看作梯形进行计算。三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,据此分析。
【详解】2×2÷2+3×1
=2+3
=5(平方厘米)
4×1÷2+(4+5)×1÷2+5×1÷2
=2+9×1÷2+2.5
=2+4.5+2.5
=9(平方厘米)
(2+4)×3÷2
=6×3÷2
=9(平方厘米)
图形A的面积是5平方厘米;图形B的面积是9平方厘米;图形C的面积大约是9平方厘米。
【点睛】关键是掌握并灵活运用三角形、平行四边形和梯形面积公式。
9. 15 900
【分析】通过平移可知,这个图形的周长相当于3个正方形的周长,已知所构成图形的周长是180厘米,用180÷3即可求出一个正方形的周长,再根据正方形的周长公式,用一个正方形的周长除以4,即可求出正方形的边长;这个图形的面积相当于4个正方形的面积;根据正方形的面积公式,代入数据求出一个正方形的面积,再乘4即可求出结果。
【详解】180÷3=60(厘米)
60÷4=15(厘米)
15×15×4=900(平方厘米)
每个正方形的边长是15厘米,整个图形覆盖的面积是900平方厘米。
【点睛】本题可通过平移巧求正方形的边长,掌握相关公式是解答本题的关键。
10.24.8
【分析】要想在这个梯形卡纸中剪去一个最大的三角形,必须把梯形的下底作为三角形的底。把梯形的高作为三角形的高,则剩下的图形的面积就是以梯形的上底为底,梯形的高为高的三角形的面积,据此利用三角形的面积公式计算即可解答。
【详解】12.4×4÷2=24.8(平方厘米)
即剩下卡纸的面积是24.8平方厘米。
【点睛】此题考查组合图形的面积,解决此题关键是弄明白怎么剪才能使三角形的面积最大,进而得出剩下的是以上底为底边的三角形的面积。
11.C
【分析】从图中可知,阴影部分的面积=长方形(或正方形)的面积-空白部分的面积,已知长方形与正方形的面积相等,如果空白部分的面积不相等,那么阴影部分的面积就不相等。
【详解】A.因为长方形与正方形的面积相等,阴影部分分别占长方形、正方形的,所以阴影部分面积相等;
B.因为长方形与正方形的面积相等,空白部分的面积也相等,所以阴影部分面积相等;
C.因为长方形的空白部分比正方形的空白部分大,所以阴影部分的面积不相等;
D.因为长方形与正方形的面积相等,空白部分的面积也相等,所以阴影部分面积相等。
故答案为:C
【点睛】本题考查组合图形面积的求法,关键是分析出阴影部分的面积是由哪些图形面积相减得到,再看这些图形面积是否相等,进而得出结论。
12.B
【分析】甲图的阴影部分是一个平行四边形,从图中可知,平行四边形的底小于正方形边长的一半,平行四边形的高等于正方形的边长;根据平行四边形的面积=底×高,正方形的面积=边长×边长,得出平行四边形的面积小于正方形面积的一半;
如下图,在乙图上画小方格,正方形共有32个小三角形,阴影部分有16个小三角形,所以乙图阴影部分的面积等于正方形面积的一半;
据此比较,得出结论。
【详解】甲图的阴影部分是一个平行四边形,平行四边形的面积小于正方形面积的一半;
乙图的阴影部分是4个小正方形,它们的面积之和等于正方形面积的一半。
因为两个正方形的面积相等,所以乙图阴影部分的面积>甲图阴影部分的面积。
综上所述,正方形中的阴影部分乙的面积更大。
故答案为:B
【点睛】本题考查组合图形面积的求法,把比较甲、乙两个图形阴影部分的面积转移到各图形阴影部分面积与正方形的面积相比较,进而得出结论。
13.D
【分析】如图:假设中间的三角形为④,平行四边形的高和对边相等,分别是h、a,则②+③+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的底乘高除以2;三角形①+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的下底乘高除以2,即可得解。
【详解】假设中间的三角形为④,平行四边形的高为h,底边长为a,
则②+③+④的面积=a×h÷2,①+④的面积=a×h÷2,
所以②+③+④=①+④,
即①=②+③。
故答案为:D
【点睛】此题关键是利用中间量,通过三角形的面积公式,从而解决问题。
14.A
【分析】根据三角形面积:,梯形面积:计算,继而比较大小即可。
【详解】A.涂色部分和空白部分是等底等高的三角形,面积相等。
B.涂色部分三角形和空白部分的梯形等高,梯形的上底+下底>三角形的底,故梯形的面积>三角形面积。
C.令梯形的高为h,则:
涂色三角形面积:
空白的两个三角形面积:
b+c>a
涂色三角形面积<空白三角形面积。
D.因梯形的上底小于下底,涂色和空白三角形等高。
则:涂色三角形面积大于空白三角形面积。
故答案为:A
【点睛】掌握三角形面积和梯形面积计算方法是解答的关键。
15.B
【分析】可以把这个脚掌看作一个长是12cm,宽是4cm的长方形,根据长方形的面积:长×宽,把数代入即可求解。
【详解】12×4=48(cm2)
如图所示,每个小正方形的面积为1cm2,请你估计一下,这枚日脚印的面积约是48cm2。
故答案为:B
【点睛】熟练掌握数格法求不规则图形的面积的方法是解答本题的关键。
16.B
【分析】连接AC,将四边形ABCD分割成△ADC与△ABC,△ADC的底是CD,高是AF,△ABC的底是AB,高是CE。△ADC的面积:5×4÷2=10(平方厘米);△ABC的面积: 2×6÷2=6(平方厘米);10+6=16(平方厘米),则四边形ABCD的面积是16平方厘米。
【详解】如图所示:
5×4÷2
=20÷2
=10(平方厘米)
2×6÷2
=12÷2
=6(平方厘米)
10+6=16(平方厘米)
则四边形ABCD的面积是16平方厘米。
故答案为:B
【点睛】本题考查三角形的面积,明确把阴影部分拆成两个三角形是解题的关键。
17.A
【分析】①可以把不规则图形看成近似于规则的图形估算面积。
②③用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
【详解】①,可以将图案转化成底是7cm,高是9cm的三角形,原方法错误。
②用数格子的方法:大于半格的记1格,不够半格的记为0,方法正确。
③方格纸上满格的有25格,都记1格,不满格的有20格,都记0,记0的太多,方法错误。
估算方法较合理的有1种。
故答案为:A
【点睛】关键是掌握不规则图形面积的估算方法。
18.×
【分析】先估算甲乙的面积各是多少,然后再进行比较,据此即可解答。
【详解】通过观察甲的面积相当于2个小方格面积,乙的面积相当于2个半方格的面积,所以乙的面积比甲大。
故答案为:错误
【点睛】本题考查学生对面积及面积的大小比较知识的掌握,解题的关键是对不规则图形面积的估算。
19.×
【详解】如果两个图形的面积相等,那么它们的形状不一定相同,所以本题说法错误;
故答案为:×
20.×
【分析】把不规则图形看成近似于规则的图形估算面积,有时候估算的面积比实际面积大,有时候估算的面积比实际面积小。
【详解】根据分析,估算的面积一般比实际面积大,说法错误。
故答案为:×
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
21.√
【分析】不规则图形面积的估算方法:可以借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
【详解】不规则图形的面积可以转化为学过的图形来估算,说法正确。
故答案为:√
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
22.√
【分析】多边形里面三角形的内角和是180°,180°的2倍是360°;正四边形的每个角是90°,90°的4倍是360°;正六边形的每个角是120°,120°的3倍是360°;因此多边形中有三角形、正四边形、正六边形可以密铺,正五边形不能密铺;长方形的每个角是90°,所以长方形可以密铺,平行四边形同一边的角和是180°,180°的2倍是360°,所以平行四边形也可以密铺;据此解答。
【详解】长方形、三角形、平行四边形、正六边形都可以单独密铺。原题干说法正确。
故答案为:√
【点睛】本题主要考查了密铺的知识,注意判断图形对应的角能否组成360°。
23.42平方厘米;26平方厘米
【分析】(1)涂色部分的面积=平行四边形的面积-三角形的面积。根据平行四边形的面积=底×高,用8×6求出平行四边形的面积(48平方厘米);三角形的底是8-3-2=3(厘米),根据三角形的面积=底×高÷2,用3×4÷2求出三角形的面积(6平方厘米);用48-6求出涂色部分的面积。
(2)如下图,涂色部分的面积=正方形ABCD的面积+正方形CEFG的面积-三角形ABD的面积-三角形BEF的面积。根据正方形的面积=边长×边长,用8×8求出正方形ABCD的面积(64平方厘米),用6×6求出正方形CEFG的面积(36平方厘米);根据三角形的面积=底×高÷2,用8×8÷2求出三角形ABD的面积(32平方厘米),用(8+6)×6÷2求出三角形BEF的面积(42平方厘米);最后用64+36-32-42求出涂色部分的面积。
【详解】8×6-(8-3-2)×4÷2
=48-3×4÷2
=48-12÷2
=48-6
=42(平方厘米)
涂色部分面积是42平方厘米。
8×8+6×6-8×8÷2-(8+6)×6÷2
=64+36-32-14×6÷2
=100-32-84÷2
=68-42
=26(平方厘米)
涂色部分面积是26平方厘米。
24.14.4千克
【分析】将数据代入三角形面积公式:S=ah÷2及平行四边形面积公式:S=ah,分别求出三角形与平行四边形的面积,求和即可求出这面广告牌的面积,最后用广告牌的面积乘每平方分米需要的涂料即可。
【详解】12×4÷2+12×6
=48÷2+72
=24+72
=96(平方分米)
96×0.15=14.4(千克)
答:一共要用14.4千克涂料。
【点睛】本题主要考查组合图形面积的求法,解题时通常将组合图形分割成基础图形,再求面积。
25.17.2平方米
【分析】根据题意,两条小路是两个底为0.5米,高为6米的平行四边形;从图中可知,空白部分的面积=长方形的面积-2个平行四边形的面积,根据长方形的面积=长×宽,平行四边形的面积=底×高,代入数据计算,求出空白部分的面积,也是五年级3个班的土地总面积;再用3个班的土地总面积除以3,即是平均每个班分到的面积。
【详解】(9.6×6-0.5×6×2)÷3
=(57.6-3×2)÷3
=(57.6-6)÷3
=51.6÷3
=17.2(平方米)
答:每个班分到了17.2平方米的土地。
【点睛】本题考查组合图形面积的求法,结合图形分析出组合图形的面积是由哪些图形的面积相加或相减得到,再根据图形的面积公式求解。
26.(1)图见详解;直角三角
(2)16.5平方厘米
【详解】(1)根据数对表示位置的方法,在方格图中标出下列各点并依次连成封闭图形,解答即可。
(2)方格图中五边形的面积等于上底是6厘米,下底是3厘米,高3厘米的梯形面积加底是6厘米,高1厘米的三角形面积,据此解答即可。
【解答】(1)在上面的方格图中标出下列各点并依次连成封闭图形。如图:
A(2,1);B(2,4);C(5,1)
这是一个直角三角形。
(2)(6+3)×3÷2+6×1÷2
=9×3÷2+6×1÷2
=13.5+3
=16.5(平方厘米)
所以五边形的面积是16.5平方厘米。
【点睛】此题考查数对位置和组合图形的面积。确定列数,一般从左往右;确定行数,一般从前往后或从下往上。用数对示位置时, 先说列,后说行。组合图形是由几个简单的图形组合而成的,其面积既可以看作几个简单图形的面积和,也可以看作几个简单图形的面积差。
27.696平方厘米
【分析】火箭模型的面积=上底是16厘米,下底是8厘米,高是8厘米的梯形面积+长是70厘米,宽是8厘米的长方形面积+底是8厘米,高是10厘米的三角形面积;根据梯形面积公式:面积=(上底+下底)×高÷2;长方形面积公式:面积=长×宽;三角形面积公式:面积=底×高÷2,代入数据,即解答。
【详解】(16+8)×8÷2+70×8+8×10÷2
=24×8÷2+560+80÷2
=192÷2+560+40
=96+560+40
=656+40
=696(平方厘米)
答:它的面积是696平方厘米。
28.425平方米
【分析】先根据长方形的面积=长×宽,用62×25求出长方形的面积;再根据梯形的面积=(上底+下底)×高÷2,用(28+62)×25÷2求出梯形的面积;最后用长方形的面积减去梯形的面积,即可求出展区面积比原来增加了多少平方米。
【详解】62×25-(28+62)×25÷2
=1550-90×25÷2
=1550-2250÷2
=1550-1125
=425(平方米)
答:展区面积比原来增加了425平方米。
29.440平方米
【分析】连接BD,如图所示:
三角形面积=底×高÷2,三角形AEF和三角形BEF高相等,并且BE=2AE,那么三角形BEF的面积是三角形AEF面积的2倍;
FG=GD,那么三角形BGD和三角形BFG等底等高,那么这两个三角形的面积相等;
同理,BH=HC,那么三角形BHD和三角形HCD等底等高,面积相等。
将空白部分的面积相加,求出种植郁金香的面积即可。
【详解】25×2=50(平方米)
50+150+150+90=440(平方米)
答:郁金香的面积是440平方米。
【点睛】本题考查了三角形的面积、组合图形的面积,熟记并灵活运用三角形的面积公式,并掌握割补法求组合图形的面积是解题的关键。
答案第1页,共2页
答案第1页,共2页
