证明一回顾与思考(山东省淄博市桓台县)
文档属性
| 名称 | 证明一回顾与思考(山东省淄博市桓台县) |

|
|
| 格式 | rar | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-17 00:00:00 | ||
图片预览



文档简介
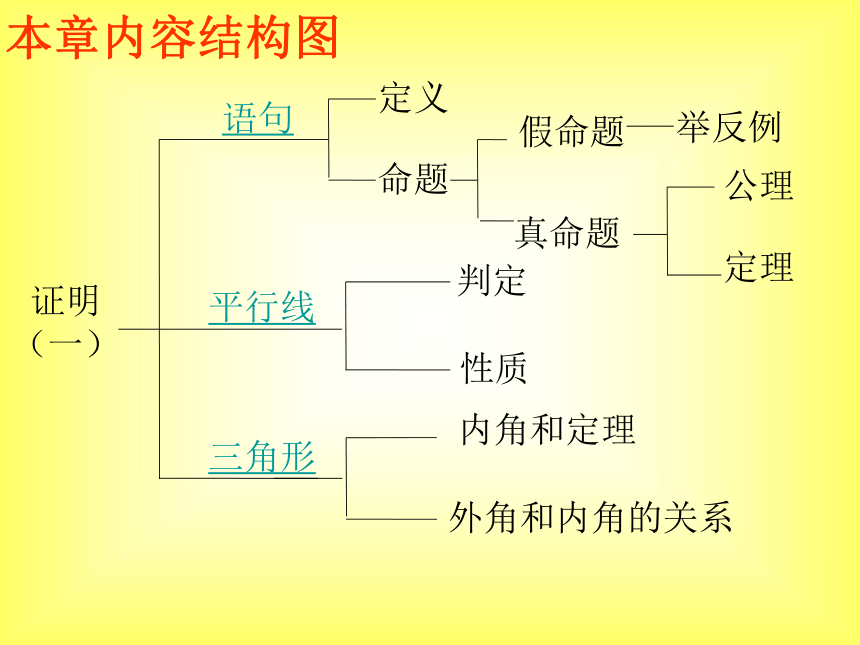
课件19张PPT。第三章证明(一)回顾与思考 本章内容结构图定义 证明
(一)语句平行线三角形命题真命题假命题公理定理判定性质内角和定理外角和内角的关系举反例追踪训练一: 1、判别下列语句是不是命题,如果是命题,
是真命题还是假命题。(1)作线段AB=CD
(2)熊猫没有翅膀
(3)你喜欢数学吗?
(4)三角形内角和是360。 2、下列命题的条件是什么?结论是什么?并判断命题的真假,若是假命题举反例说明。(2) 对顶角相等;
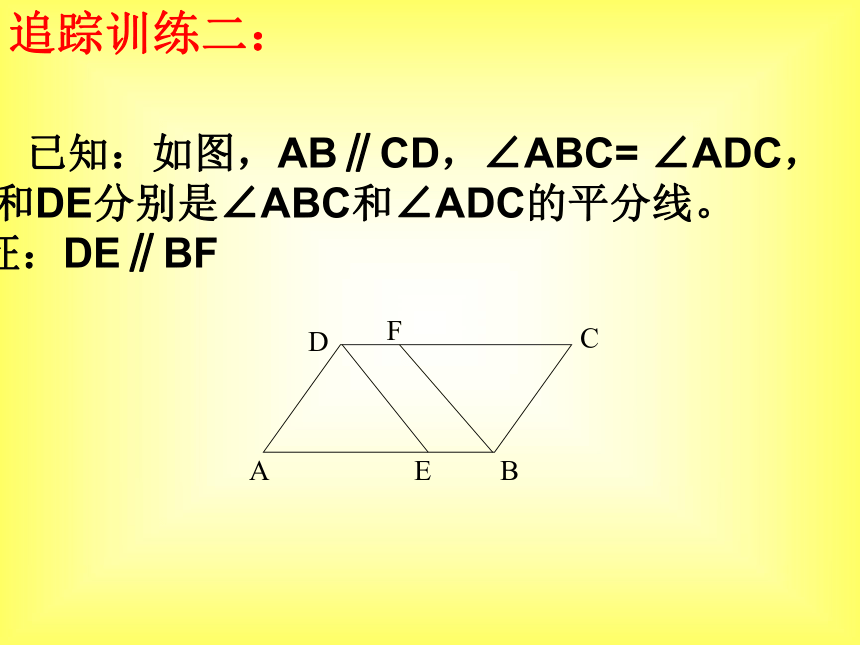
(1)如果a>b,b>c,那么a>c;(3)两角和其中一角的对边对应相等的两个 三角形全等;(4) 如果两个角相等,那么它们是对顶角. 1、已知:如图,AB∥CD,∠ABC= ∠ADC,
BF和DE分别是∠ABC和∠ADC的平分线。
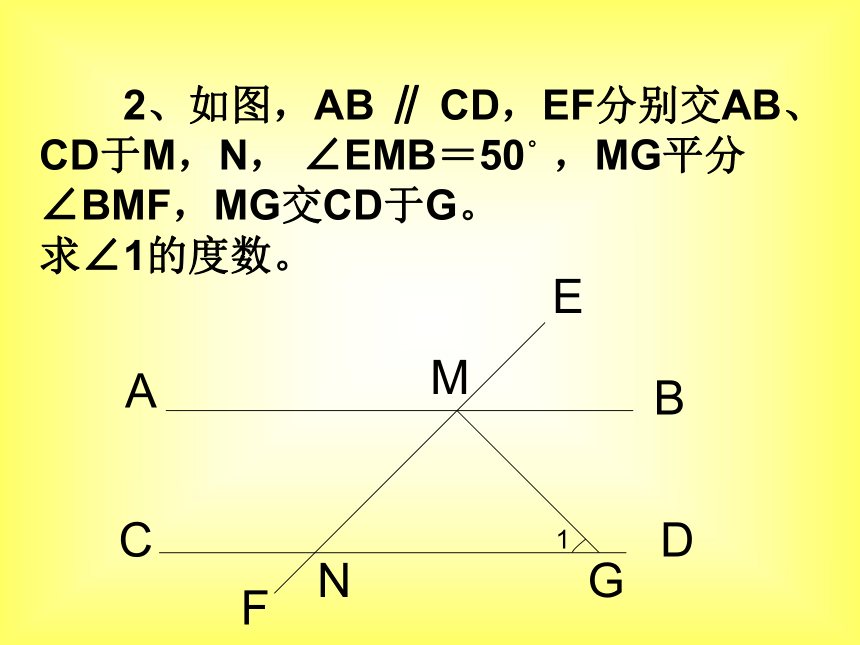
求证:DE∥BFABCDEF追踪训练二: 2、如图,AB ∥ CD,EF分别交AB、CD于M,N, ∠EMB=50。,MG平分∠BMF,MG交CD于G。
求∠1的度数。
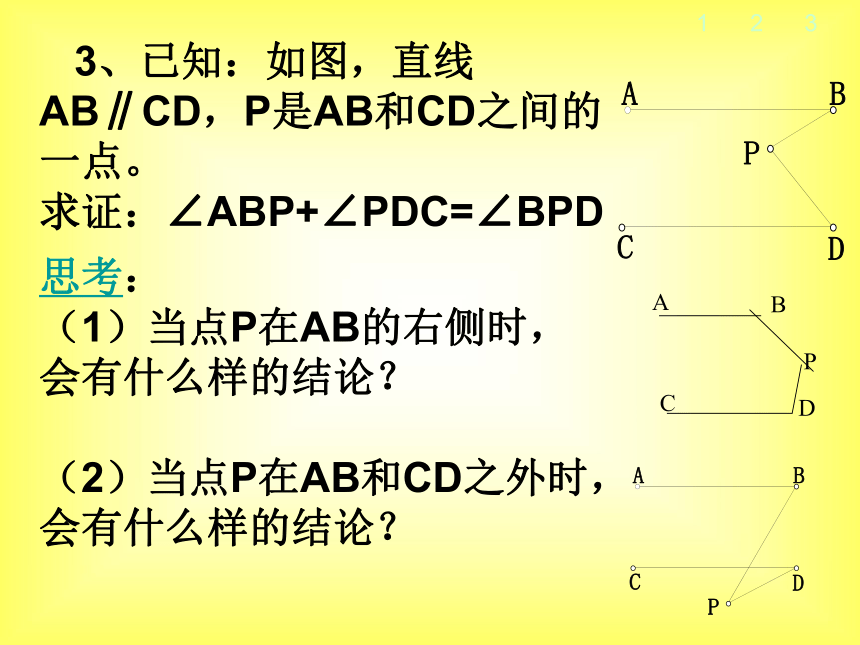
MBEACDFNG1 3、已知:如图,直线AB∥CD,P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD123 3、已知:如图,直线AB∥CD,
P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD证明:过点P作PM∥AB。
∵AB∥CD(已知)
∴PM∥CD(平行的性质)。
∴∠PDC=∠MPD(两直线平行,内错角相等)
∠BPM=∠ABP(两直线平行,内错角相等)
∵∠BPD=∠BPM+∠MPD
∴∠ABP+∠PDC=∠BPD(等量代换)。 3、已知:如图,直线AB∥CD,
P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD证明:延长DP交AB于点M。
∵AB∥CD( 已知),
∴∠BMP =∠PDC(两直线平行,内错角相等)。
∵∠BPD=∠BMP +∠ABP(三角形的一个外角等于和它不相邻的两个内角的和),
∴∠ABP+∠PDC=∠BPD(等量代换)。 3、已知:如图,直线AB∥CD,P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD证明:连接BD。
∵AB∥CD( 已知),
∴∠ABD+∠BDC=180°(两直线平行,同旁内角互补),
即∠ABP+∠PBD+∠PDB+∠PDC=180°。
∵∠BPD+∠PBD +∠PDB=180°(三角形内角和等于180°),
∴∠ABP+∠PDC=∠BPD(等量代换)。 ∠ABP+∠BPD+∠PDC=_____∠ABC=∠C+∠D 1、已知BD为△ ABC的角平分线,CD为
△ ABC的外角∠ACE的角平分线,它与
BD相交于D,如图所示。
求证: ∠A=2 ∠DABCED1234追踪训练三:
2、已知:如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE。
求证:∠1>∠2。(一)填空题
1.如图,直线c与直线a、b相交,
且a//b,若∠1=40°,则∠2=____.
2.如图所示,∠A=60o,∠B=70o,∠1=∠2,DE∥BC,则∠3=______,∠4=______.
3.如图所示,△ABC中,∠B=∠C,
E是AC上一点,ED⊥BC,DF⊥AB,
垂足分别为D、F,若∠AED=140o,
则∠C= ___ ∠A=____ ∠BDF=___ . 课堂训练
4.已知下列命题:
①相等的角是对顶角;②互补的角就是平角;
③互补的两个角一定是一个锐角,另一个为钝角;
④平行于同一条直线的两直线平行;
⑤邻补角的平分线互相垂直.
其中,正确命题的个数为( ).
A.0个 B.1个 C.2个 D.3个(二)选择题C5.如图,如果AB∥CD,则角α、β、γ之间的关系式为( ).
A.α+β+γ=360o
B.α-β+γ=180o
C.α+β+γ=180o
D.α+β-γ=180o D6.已知:△ABC中,∠A=∠B,CE是外角∠BCD的平分线.
求证:CE∥AB. 12 对于青少年,最关键的是从小要有好奇心,遇到问题追问下去。这种精神比考试得到好分数更重要。 ?????
——李政道 ???? 教师寄语挑战极限: 如图,有两条平行直线m、n,AOB是两平行线间的一条折线,则我们会有这样的结论:
∠o= ∠1+ ∠2.
(1)如果将折一次改为折两次如图,些时∠1、 ∠2、 ∠ 3、∠4会满足怎样的关系?证明你的结论。(2)若此折线折三次、折四次······折n次呢?
(一)语句平行线三角形命题真命题假命题公理定理判定性质内角和定理外角和内角的关系举反例追踪训练一: 1、判别下列语句是不是命题,如果是命题,
是真命题还是假命题。(1)作线段AB=CD
(2)熊猫没有翅膀
(3)你喜欢数学吗?
(4)三角形内角和是360。 2、下列命题的条件是什么?结论是什么?并判断命题的真假,若是假命题举反例说明。(2) 对顶角相等;
(1)如果a>b,b>c,那么a>c;(3)两角和其中一角的对边对应相等的两个 三角形全等;(4) 如果两个角相等,那么它们是对顶角. 1、已知:如图,AB∥CD,∠ABC= ∠ADC,
BF和DE分别是∠ABC和∠ADC的平分线。
求证:DE∥BFABCDEF追踪训练二: 2、如图,AB ∥ CD,EF分别交AB、CD于M,N, ∠EMB=50。,MG平分∠BMF,MG交CD于G。
求∠1的度数。
MBEACDFNG1 3、已知:如图,直线AB∥CD,P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD123 3、已知:如图,直线AB∥CD,
P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD证明:过点P作PM∥AB。
∵AB∥CD(已知)
∴PM∥CD(平行的性质)。
∴∠PDC=∠MPD(两直线平行,内错角相等)
∠BPM=∠ABP(两直线平行,内错角相等)
∵∠BPD=∠BPM+∠MPD
∴∠ABP+∠PDC=∠BPD(等量代换)。 3、已知:如图,直线AB∥CD,
P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD证明:延长DP交AB于点M。
∵AB∥CD( 已知),
∴∠BMP =∠PDC(两直线平行,内错角相等)。
∵∠BPD=∠BMP +∠ABP(三角形的一个外角等于和它不相邻的两个内角的和),
∴∠ABP+∠PDC=∠BPD(等量代换)。 3、已知:如图,直线AB∥CD,P是AB和CD之间的一点。
求证:∠ABP+∠PDC=∠BPD证明:连接BD。
∵AB∥CD( 已知),
∴∠ABD+∠BDC=180°(两直线平行,同旁内角互补),
即∠ABP+∠PBD+∠PDB+∠PDC=180°。
∵∠BPD+∠PBD +∠PDB=180°(三角形内角和等于180°),
∴∠ABP+∠PDC=∠BPD(等量代换)。 ∠ABP+∠BPD+∠PDC=_____∠ABC=∠C+∠D 1、已知BD为△ ABC的角平分线,CD为
△ ABC的外角∠ACE的角平分线,它与
BD相交于D,如图所示。
求证: ∠A=2 ∠DABCED1234追踪训练三:
2、已知:如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE。
求证:∠1>∠2。(一)填空题
1.如图,直线c与直线a、b相交,
且a//b,若∠1=40°,则∠2=____.
2.如图所示,∠A=60o,∠B=70o,∠1=∠2,DE∥BC,则∠3=______,∠4=______.
3.如图所示,△ABC中,∠B=∠C,
E是AC上一点,ED⊥BC,DF⊥AB,
垂足分别为D、F,若∠AED=140o,
则∠C= ___ ∠A=____ ∠BDF=___ . 课堂训练
4.已知下列命题:
①相等的角是对顶角;②互补的角就是平角;
③互补的两个角一定是一个锐角,另一个为钝角;
④平行于同一条直线的两直线平行;
⑤邻补角的平分线互相垂直.
其中,正确命题的个数为( ).
A.0个 B.1个 C.2个 D.3个(二)选择题C5.如图,如果AB∥CD,则角α、β、γ之间的关系式为( ).
A.α+β+γ=360o
B.α-β+γ=180o
C.α+β+γ=180o
D.α+β-γ=180o D6.已知:△ABC中,∠A=∠B,CE是外角∠BCD的平分线.
求证:CE∥AB. 12 对于青少年,最关键的是从小要有好奇心,遇到问题追问下去。这种精神比考试得到好分数更重要。 ?????
——李政道 ???? 教师寄语挑战极限: 如图,有两条平行直线m、n,AOB是两平行线间的一条折线,则我们会有这样的结论:
∠o= ∠1+ ∠2.
(1)如果将折一次改为折两次如图,些时∠1、 ∠2、 ∠ 3、∠4会满足怎样的关系?证明你的结论。(2)若此折线折三次、折四次······折n次呢?
