对数函数及其性质

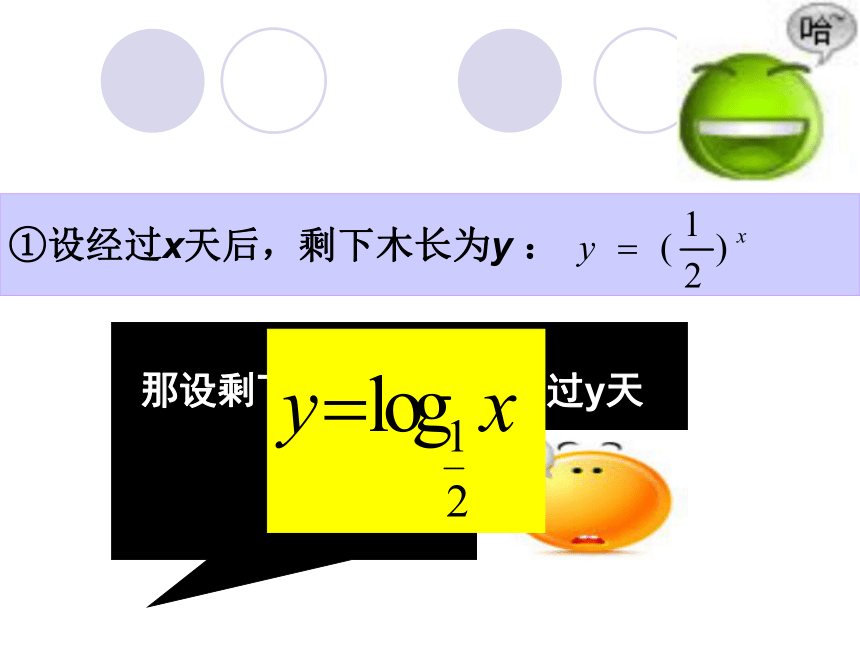
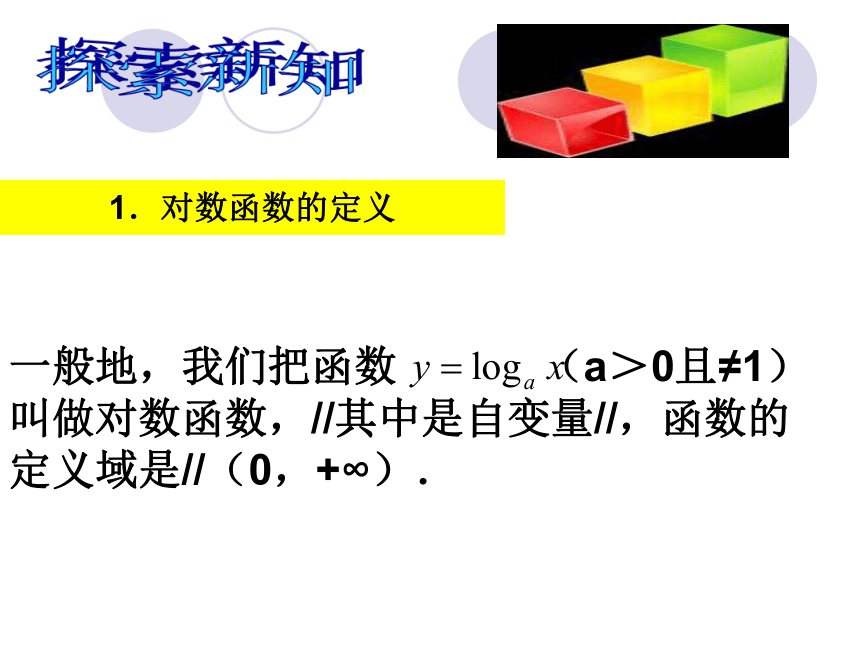
课件20张PPT。2.2.2对数函数及其性质第一课时情景思考《庄子》: “一尺之木，日截其半，万世不竭”。 问题1：你能从中发现其中的函数关系吗?①设经过x天后，剩下木长为y ： 那设剩下木长为x，要经过y天 探索新知1．对数函数的定义一般地，我们把函数 （a＞0且≠1）叫做对数函数，//其中是自变量//，函数的定义域是//（0，+∞）． 例1、求下列函数的定义域（1） （2）
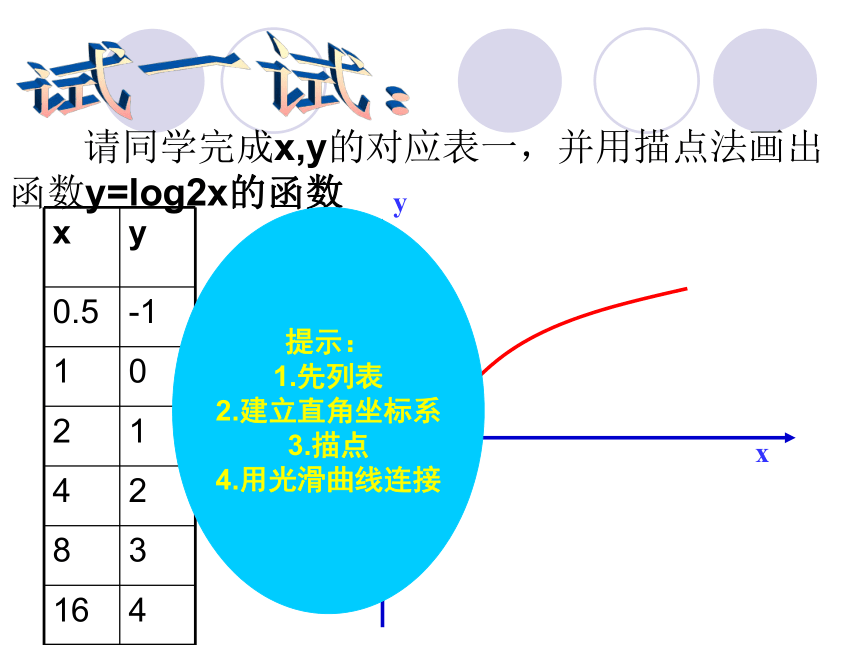
//变式1： //变式2：试一试： 请同学完成x,y的对应表一，并用描点法画出函数y=log2x的函数1o提示：
1.先列表
2.建立直角坐标系
3.描点
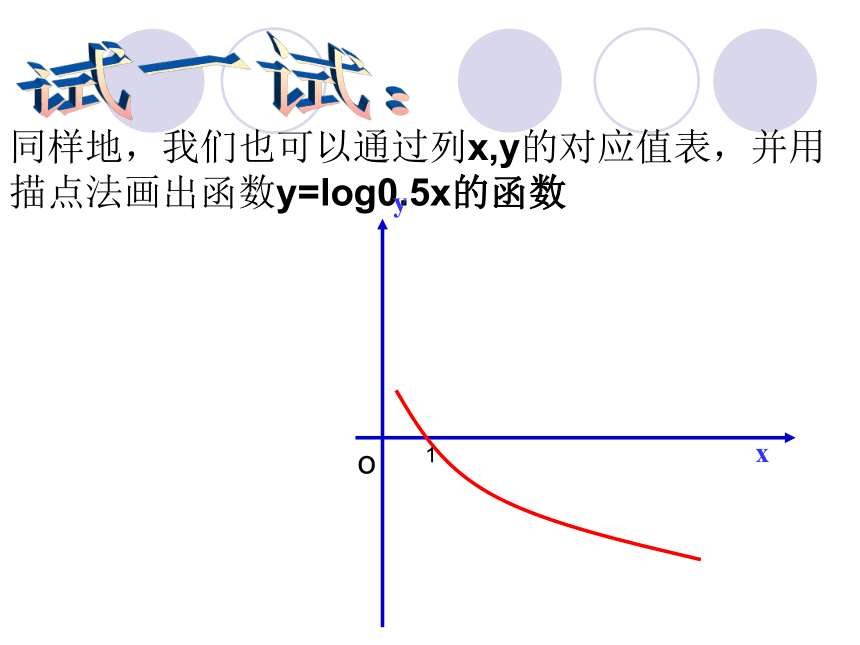
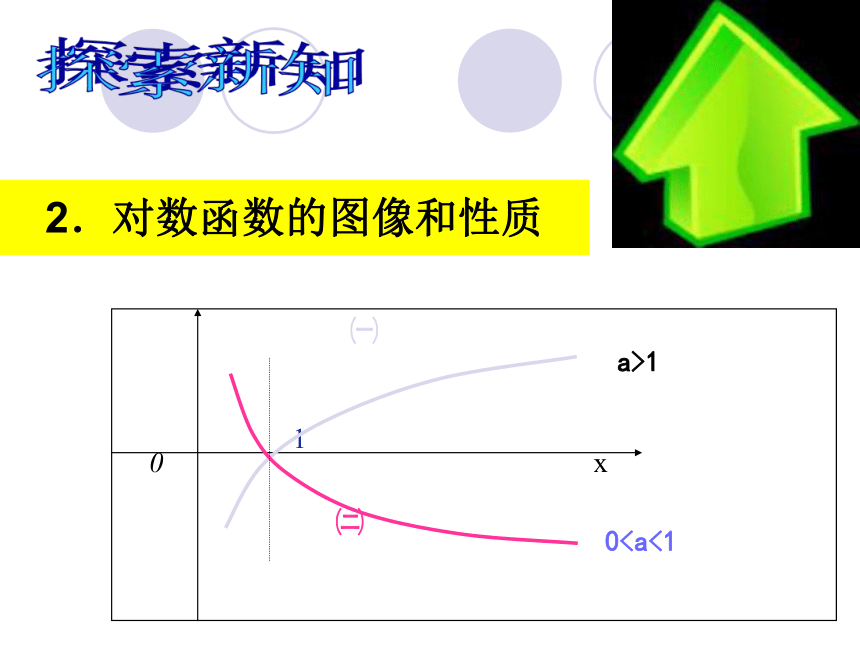
4.用光滑曲线连接试一试：同样地，我们也可以通过列x,y的对应值表，并用描点法画出函数y=log0.5x的函数1o探索新知2．对数函数的图像和性质图象特征和
性质的分析yy(1,0)下上逐渐上升逐渐下降定义域:( 0,＋∞）;值域:Rloga1=0当a>1时， x∈(0,1)时，y<0
x∈(1,+∞)时,y>0
当01时，y=logax在( 0,＋∞) 是增函数;
当0猜想下列对数函数分别对应图中哪个函数图象？ 猜想与思考：对应 ；
对应 ；
对应 ；
活动：画出下列对数函数的草图,并用草图验证上面的猜想：① ②问题3：探索对数函数的性质（1）回顾：我们研究过指数函数哪几方面的性质？2）类比指数函数的性质，并结合对数函数的图像，你能发现对数函数的性质吗？例2.对数函数性质应用例2、比较下列各组数中两个值的大小

（2）（3）比较正数m，n的大小(1)(4)(a＞0，且 a≠1）问题4：你能总结出比较两个同底对数值大小的一般步骤吗？对数函数y=log a x (a>0, a≠1)(4) 当0 当x>1时, y>0(4) 当00;
当x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域： (0,+∞)(2) 值域：Rxyo(1, 0)xyo（1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质探索比较下列各组数中的两个值大小（1）
（2）课堂练习 教材P73： 2、3再见!