12.2.2-3实数的运算
图片预览






文档简介
(共19张PPT)
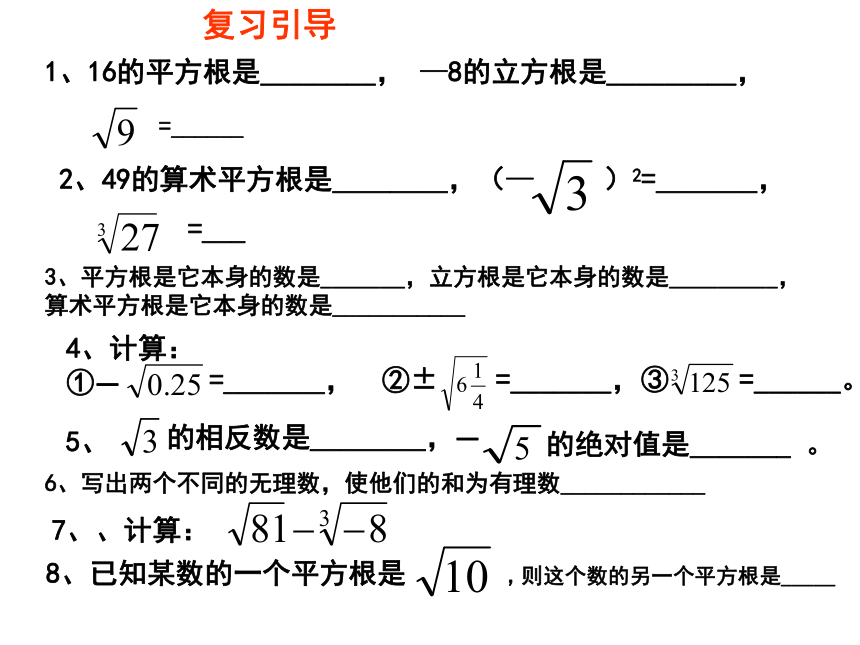
1、16的平方根是________, —8的立方根是_________,
=______
2、49的算术平方根是________,(—
)2=_______,
=___
3、平方根是它本身的数是_______,立方根是它本身的数是_________,算术平方根是它本身的数是___________
4、计算:①—
=_______, ②±
=_______,③
=______。
5、
的相反数是________,—
的绝对值是_______ 。
6、写出两个不同的无理数,使他们的和为有理数____________
7、、计算:
8、已知某数的一个平方根是 ,则这个数的另一个平方根是_____
复习引导
例1:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)
1.在数轴上表示的两个实数,右边的数总比左边的数大。
2.两个带根号的数可以比较被开方数,被开方数大,其根就大。
一、实数的大小比较与有理数的大小比较
例2、比较大小: 与
试一试:比较下列各组数的大小:
(1) 3
(2) 与 2
√2
与 2
√5
√3
例3、试估计 与π的大小关系.
分析:用计算器求得
而
这样,容易判断
实数的大小比较和运算,通常可取它们的近似值来进行。
注意:有些数不能直接比较,可以借助计算器求近似值比较。
7
22
π与
练习:
例4、计算: (结果精确到0.01)
解: 用计算器求得:
于是
所以
例5、已知实数a、b在数轴上对应点的位置如图1-2;
化简:
b a o
x
解:由图知:b<a<0,
∴a-b>0,a+b<0.
∴|a-b|+
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
=(a-b)+|a+b|
3、绝对值等于 的数是 , 的平方 是 .
随堂练习
填空
2、 的相反数是 ,绝对值是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
5、一个数的绝对值是 ,则这个数是 .
实数和有理数一样,也可以进行加、减、乘、除、乘方运算。
而且有理数的运算法则与运算律对实数仍然成立。
1.交换律: 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a×(b+c)=a×b+a×c
实数的运算顺序
(1) 先算乘方和开方;
(2)再算乘除,最后算加;
(3)如果遇到括号, 则先进行括号里的运算
例6:计算
解:原式=
=
=
=
解:原式=[-9×2+3×(-8)+24]÷[-9]
=(-18-24+24)÷(-9)
=2
例7、
计算:[-32×2+3×(-2)3-4×(-6)]÷[- ].
;
2. 2×(
)—2×(
—
—
练习
3.
4.
例8
解:原式=
(1)
(2)
(3).数轴上A,B两点分别表示实数 和 ,求A,B两点之间的距离。
例9、若
求 的值。
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-4/3,b=3/4
∴ab=(-4/3)·(3/4)=-1
解:∵1 < 3 < 4
∴a=3,b=
8. 无理数与有理数的积是无理数. ( )
1. 无限小数是无理数. ( )
下列说法正确与否, 若错则举例说明:
想一想
×
2. 无理数是无限小数. ( )
√
3. 无理数就是开不尽根的数. ( )
×
4. 带根号的数都是无理数. ( )
×
5. 无理数与无理数的和是无理数. ( )
6. 无理数与有理数的和是无理数. ( )
7. 无理数与无理数的积是无理数. ( )
×
×
×
√
9. 任何无理数的绝对值总是正数. ( )
√
作业
1计算
2. 化简计算:
⑴ -2 + -3 - -3
√3
√5
√5
√2
⑵ 1- + - + -
√3
√3
√2
√5
3. 比较下列各组数的大小:
√2
+ 与π
√3
4.已知 a 是 的整数部分,b是 的小数部分,求:2a-b
1、16的平方根是________, —8的立方根是_________,
=______
2、49的算术平方根是________,(—
)2=_______,
=___
3、平方根是它本身的数是_______,立方根是它本身的数是_________,算术平方根是它本身的数是___________
4、计算:①—
=_______, ②±
=_______,③
=______。
5、
的相反数是________,—
的绝对值是_______ 。
6、写出两个不同的无理数,使他们的和为有理数____________
7、、计算:
8、已知某数的一个平方根是 ,则这个数的另一个平方根是_____
复习引导
例1:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)
1.在数轴上表示的两个实数,右边的数总比左边的数大。
2.两个带根号的数可以比较被开方数,被开方数大,其根就大。
一、实数的大小比较与有理数的大小比较
例2、比较大小: 与
试一试:比较下列各组数的大小:
(1) 3
(2) 与 2
√2
与 2
√5
√3
例3、试估计 与π的大小关系.
分析:用计算器求得
而
这样,容易判断
实数的大小比较和运算,通常可取它们的近似值来进行。
注意:有些数不能直接比较,可以借助计算器求近似值比较。
7
22
π与
练习:
例4、计算: (结果精确到0.01)
解: 用计算器求得:
于是
所以
例5、已知实数a、b在数轴上对应点的位置如图1-2;
化简:
b a o
x
解:由图知:b<a<0,
∴a-b>0,a+b<0.
∴|a-b|+
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
=(a-b)+|a+b|
3、绝对值等于 的数是 , 的平方 是 .
随堂练习
填空
2、 的相反数是 ,绝对值是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
5、一个数的绝对值是 ,则这个数是 .
实数和有理数一样,也可以进行加、减、乘、除、乘方运算。
而且有理数的运算法则与运算律对实数仍然成立。
1.交换律: 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a×(b+c)=a×b+a×c
实数的运算顺序
(1) 先算乘方和开方;
(2)再算乘除,最后算加;
(3)如果遇到括号, 则先进行括号里的运算
例6:计算
解:原式=
=
=
=
解:原式=[-9×2+3×(-8)+24]÷[-9]
=(-18-24+24)÷(-9)
=2
例7、
计算:[-32×2+3×(-2)3-4×(-6)]÷[- ].
;
2. 2×(
)—2×(
—
—
练习
3.
4.
例8
解:原式=
(1)
(2)
(3).数轴上A,B两点分别表示实数 和 ,求A,B两点之间的距离。
例9、若
求 的值。
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-4/3,b=3/4
∴ab=(-4/3)·(3/4)=-1
解:∵1 < 3 < 4
∴a=3,b=
8. 无理数与有理数的积是无理数. ( )
1. 无限小数是无理数. ( )
下列说法正确与否, 若错则举例说明:
想一想
×
2. 无理数是无限小数. ( )
√
3. 无理数就是开不尽根的数. ( )
×
4. 带根号的数都是无理数. ( )
×
5. 无理数与无理数的和是无理数. ( )
6. 无理数与有理数的和是无理数. ( )
7. 无理数与无理数的积是无理数. ( )
×
×
×
√
9. 任何无理数的绝对值总是正数. ( )
√
作业
1计算
2. 化简计算:
⑴ -2 + -3 - -3
√3
√5
√5
√2
⑵ 1- + - + -
√3
√3
√2
√5
3. 比较下列各组数的大小:
√2
+ 与π
√3
4.已知 a 是 的整数部分,b是 的小数部分,求:2a-b
