12.1.1同底数幂的乘法 课件(共20张PPT)
文档属性
| 名称 | 12.1.1同底数幂的乘法 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 745.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 12:35:39 | ||
图片预览








文档简介
(共20张PPT)
13.1.1 同底数幂的乘法
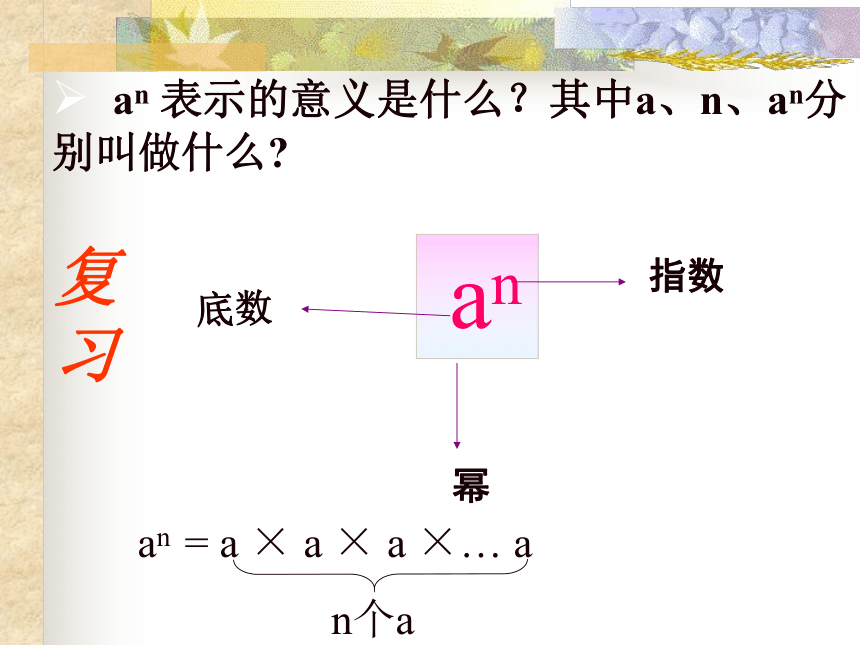
an 表示的意义是什么?其中a、n、an分 别叫做什么
an
底数
幂
指数
an = a × a × a ×… a
n个a
复习
试一试:
=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57
(1) 23 ×24
(2) 53×54
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
=a7 (乘方的意义)
继续探索:
(3) a3 · a4
=(a · a · a) (a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
这几道题有什么共同的特点呢 计算的结果有什么规律吗
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
(4)am · an =
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
知识推导
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
运算前提
运算方法
(同底、乘法)
(底不变、指相加)
幂的底数必须相同,
相乘时指数才能相加.
(4)108 ×105=
1013
108+5=
am · an = am+n
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
=23+4
=53+4
=a3+4
例1:计算
(3) a · a3 · a5 = a4 · a5 =a9
(1) 103×104 (2) a · a3 (3)a · a3 · a5
解:(1) 103×104 =103+4 =107
(2) a · a3 = a 1+3=a4
注意:当一个幂没有标指数时,其指数为1,切不可当作是0。
a · a3 · a5 = a4 · a5 =a9
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
强调:同底数幂公式同样适用于三个或三个以上同底数幂相乘.
(1)23×24×25 (2)y · y2 · y3
解:(1)23×24×25
=23+4+5
=212
(2)y · y2 · y3
=y1+2+3
=y6
例2.计算:
效果检测
x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (4)x2·x2=2x4 ( )
(5)a2·a3 - a3·a2 = 0 ( )
(6)x3·y5=(xy)8 ( ) (7) x7+x7=x14 ( )
√
×
×
×
×
×
×
1.判断(正确的打“√”,错误的打“×”)
随堂练习
2. 计算:
(1)52×57 ; (2)7×73×72;
(3)-x2·x3;(4)(-c)3·(-c)m.
(5)(-3)7×(-3)6;(6)(-7)3 ×(-7);
(7)-x3 x5; (8)b2m b2m+1
练习:已知:am=3, an=8.求am+n =?
解: am+n = am · an
=2 × 3
=6
注意:同底数幂乘法公式可以逆用,并可以解答相关的许多题。
例3.已知:am=2, an=3.求am+n =?
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x2 ·x3 = x6 ( ) (4)(-7)8 · 7 3 = (-7)11 ( )
(5)a · a6 = a6 ( ) (6)m + m3 = m4 ( )
b5 · b5= b10
b5 + b5 = 2b5
x2 · x3 = x5
(-7)8 · 73 = 711
a · a6 = a7
m + m3 = m + m3
通过上面的练习你认为同底数幂的乘法法则的应用应注意什么
1.同底数幂相乘时,指数是相加的 ,
2.注意 am · an 与am + an的区别,
3.不能疏忽指数为1的情况,
4.计算过程小心符号。
×
×
×
×
×
×
例5、计算:
强调:1.公式中的a可代表一个数、字母、式子等。
2.底数互为相反数的幂,可看作同底数幂,但运用公式
前必须先统一底数。一般采取转化指数为偶数的幂。
例6.已知:an-3×a2n+1=a10,求n
试一试:如果2n=2,2m=8,则3n × 3 m =____.
解:∵an-3×a2n+1=a10
∴an-3+2n+1=a10
∴n-3+2n+1=10
解得:n=4
判断.
(1) 52×53=55
(2) a5+a5=a10
(3) m3.(-m)3=m6
(4) a6-a2.a3=a6-a6=0
(5) (a-b)2.(b-a)3=-(b-a)5
练习
1.计算
(1)a3.(-a)4 (2)m5.(- m4) (3)(x-y)2.(y-x)
(4)(y-x)3.(x-y)2.(y-x)5
2.长方形地块的长为105m,宽为104 m,则面积为__m2
作 业
(5)b2· b3+b · b4
13.1.1 同底数幂的乘法
an 表示的意义是什么?其中a、n、an分 别叫做什么
an
底数
幂
指数
an = a × a × a ×… a
n个a
复习
试一试:
=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57
(1) 23 ×24
(2) 53×54
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
=a7 (乘方的意义)
继续探索:
(3) a3 · a4
=(a · a · a) (a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
这几道题有什么共同的特点呢 计算的结果有什么规律吗
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
(4)am · an =
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
知识推导
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
运算前提
运算方法
(同底、乘法)
(底不变、指相加)
幂的底数必须相同,
相乘时指数才能相加.
(4)108 ×105=
1013
108+5=
am · an = am+n
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
=23+4
=53+4
=a3+4
例1:计算
(3) a · a3 · a5 = a4 · a5 =a9
(1) 103×104 (2) a · a3 (3)a · a3 · a5
解:(1) 103×104 =103+4 =107
(2) a · a3 = a 1+3=a4
注意:当一个幂没有标指数时,其指数为1,切不可当作是0。
a · a3 · a5 = a4 · a5 =a9
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
强调:同底数幂公式同样适用于三个或三个以上同底数幂相乘.
(1)23×24×25 (2)y · y2 · y3
解:(1)23×24×25
=23+4+5
=212
(2)y · y2 · y3
=y1+2+3
=y6
例2.计算:
效果检测
x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (4)x2·x2=2x4 ( )
(5)a2·a3 - a3·a2 = 0 ( )
(6)x3·y5=(xy)8 ( ) (7) x7+x7=x14 ( )
√
×
×
×
×
×
×
1.判断(正确的打“√”,错误的打“×”)
随堂练习
2. 计算:
(1)52×57 ; (2)7×73×72;
(3)-x2·x3;(4)(-c)3·(-c)m.
(5)(-3)7×(-3)6;(6)(-7)3 ×(-7);
(7)-x3 x5; (8)b2m b2m+1
练习:已知:am=3, an=8.求am+n =?
解: am+n = am · an
=2 × 3
=6
注意:同底数幂乘法公式可以逆用,并可以解答相关的许多题。
例3.已知:am=2, an=3.求am+n =?
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x2 ·x3 = x6 ( ) (4)(-7)8 · 7 3 = (-7)11 ( )
(5)a · a6 = a6 ( ) (6)m + m3 = m4 ( )
b5 · b5= b10
b5 + b5 = 2b5
x2 · x3 = x5
(-7)8 · 73 = 711
a · a6 = a7
m + m3 = m + m3
通过上面的练习你认为同底数幂的乘法法则的应用应注意什么
1.同底数幂相乘时,指数是相加的 ,
2.注意 am · an 与am + an的区别,
3.不能疏忽指数为1的情况,
4.计算过程小心符号。
×
×
×
×
×
×
例5、计算:
强调:1.公式中的a可代表一个数、字母、式子等。
2.底数互为相反数的幂,可看作同底数幂,但运用公式
前必须先统一底数。一般采取转化指数为偶数的幂。
例6.已知:an-3×a2n+1=a10,求n
试一试:如果2n=2,2m=8,则3n × 3 m =____.
解:∵an-3×a2n+1=a10
∴an-3+2n+1=a10
∴n-3+2n+1=10
解得:n=4
判断.
(1) 52×53=55
(2) a5+a5=a10
(3) m3.(-m)3=m6
(4) a6-a2.a3=a6-a6=0
(5) (a-b)2.(b-a)3=-(b-a)5
练习
1.计算
(1)a3.(-a)4 (2)m5.(- m4) (3)(x-y)2.(y-x)
(4)(y-x)3.(x-y)2.(y-x)5
2.长方形地块的长为105m,宽为104 m,则面积为__m2
作 业
(5)b2· b3+b · b4
