12.3.1.1平方差公式(第一课时) 课件(共23张PPT)
文档属性
| 名称 | 12.3.1.1平方差公式(第一课时) 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 15:31:43 | ||
图片预览







文档简介
(共23张PPT)
第一课时
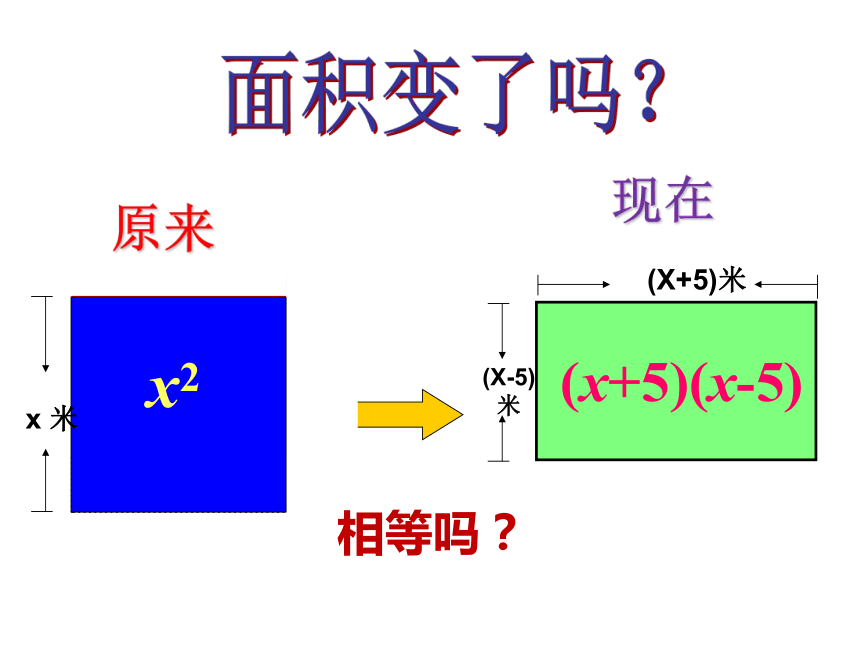
从前有一个狡猾的地主,他把一块边长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?” 聪明的同学们,你觉得这个买卖公平吗?
5米
5米
x 米
(X-5)米
(X+5)米
相等吗?
原来
现在
x2
(x+5)(x-5)
(x + 2)( x+5)
=x2
+(2+5)X
+10
=x2
+7x
两个一次二项式如何计算的?
+10
(x+a)(x+b)
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
=x2 - 12
=m2 - 22
=(2x)2 - 12
X2-1
m2-4
4x2-1
想想:结果两项与前面每项有何关系?
结论:(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
验证:
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差。
两数和乘以这两数的差
又叫平方差公式
注:这里的两数可以是两个单项式,也可以是两个多项式等等。
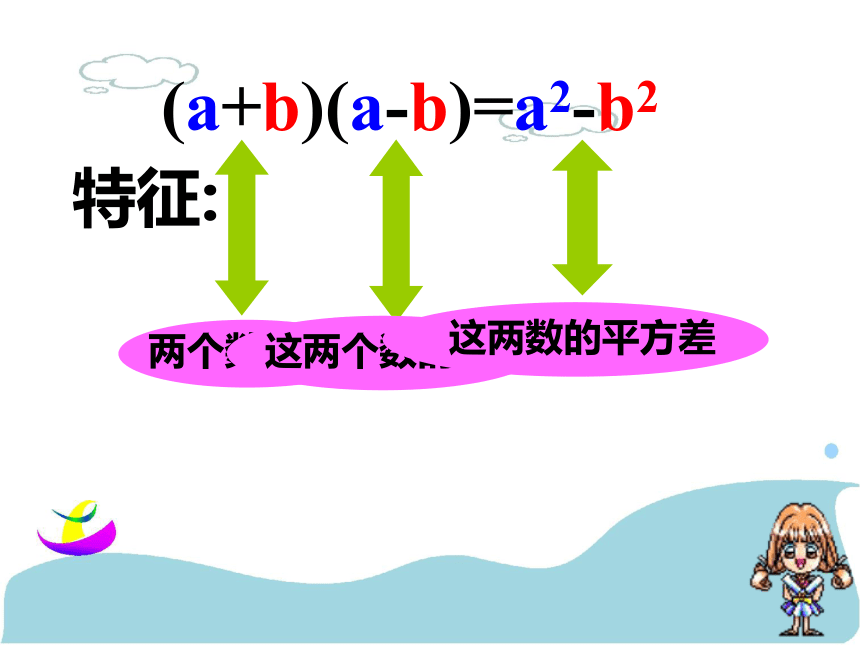
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
两数和乘以它们的差公式:
(a+b)(a-b)= a - b
两数和与它们的差的积,等于这两数的平方差。
条件:
⑴二项式×二项式;
⑵两个二项式中,有两个完全相同项, 两个互为相反数的项。
结论:
⑴ 两项的平方差;
⑵ (完全相同项)2
-(互为相反项)2
简记:
=
+
-
( )
( )
-
2
2
表示一个单项式或者多项式
“ ”
〖 〗
注意:
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
根据公式填空:
下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)
A
C
试一试
(a + b ) ( a – b ) = a2 - b2
例1、用平方差公式计算
计算:(x+2y)(x-2y)
解:原式= x2 - (2y)2
=x2 - 4y2
注意
1.先把要计算的式子与公式对照,
2.哪个是 a
哪个是 b
3.最后结果不能有乘方形式
口答下列各题:
(l)(-a+b)(a+b)= _________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
a2-b2
a2-b2
b2-a2
b2-a2
⑴ (a+3)(a-3)
⑵ (2x+y)(2x-y)
⑶ (1+2c)(1-2c )
⑷ (2a+3b)(2a-3b)
请同学们自己计算一下:
例 2
= a -3
= (2x) - y
= 1 -(2c)
= (2a) - (3b)
= 4x - y
= 1- 4c
= 4a - 9b
= a -9
解:
练习: 运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
⑵ (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).
(4) (a+3b)(a-3b)
(5) (3+2a)(-3+2a)
能运用平方差公式计算的其他形式:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
计算
本节课你的收获是什么?
试用语言表述平方差公式 (a+b)(a b)=x2 b2。
应用平方差公式 时要注意一些什么?
两数和与这两数差的积,等于它们的平方差。
变成公式标准形式后,再用公式。
或提取两“ ”号中的“ ”号,
运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式;
要利用加法交换律,
对于不符合平方差公式标准形式者,
1判断
⑴.(m+3n)(m-3n)=m -3n ( )⑵.(- m+3n)(m-3n)=m -9n ( )⑶.(- m - 3n)(- m + 3n)=m -9n ( )⑷.(m-3n) = m -9n ( )
作业
1.(m+2n)(-2n+m) 2.(-2x-y) (2x-y)
3.(-2a+3b)(-2a+3b) 4.(x2+y2)(x2-y2)
2计算
3.下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a) C.(2a-3b)(3a+2b)
D.(a-b)(b-a) E.(x-2y)(2y+x) F.(-x+2y)(-x-2y)
G.(-2y-x)(x+2y) H.(-2b-5)(2b-5)
第一课时
从前有一个狡猾的地主,他把一块边长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?” 聪明的同学们,你觉得这个买卖公平吗?
5米
5米
x 米
(X-5)米
(X+5)米
相等吗?
原来
现在
x2
(x+5)(x-5)
(x + 2)( x+5)
=x2
+(2+5)X
+10
=x2
+7x
两个一次二项式如何计算的?
+10
(x+a)(x+b)
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
=x2 - 12
=m2 - 22
=(2x)2 - 12
X2-1
m2-4
4x2-1
想想:结果两项与前面每项有何关系?
结论:(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
验证:
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差。
两数和乘以这两数的差
又叫平方差公式
注:这里的两数可以是两个单项式,也可以是两个多项式等等。
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
两数和乘以它们的差公式:
(a+b)(a-b)= a - b
两数和与它们的差的积,等于这两数的平方差。
条件:
⑴二项式×二项式;
⑵两个二项式中,有两个完全相同项, 两个互为相反数的项。
结论:
⑴ 两项的平方差;
⑵ (完全相同项)2
-(互为相反项)2
简记:
=
+
-
( )
( )
-
2
2
表示一个单项式或者多项式
“ ”
〖 〗
注意:
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
根据公式填空:
下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)
A
C
试一试
(a + b ) ( a – b ) = a2 - b2
例1、用平方差公式计算
计算:(x+2y)(x-2y)
解:原式= x2 - (2y)2
=x2 - 4y2
注意
1.先把要计算的式子与公式对照,
2.哪个是 a
哪个是 b
3.最后结果不能有乘方形式
口答下列各题:
(l)(-a+b)(a+b)= _________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
a2-b2
a2-b2
b2-a2
b2-a2
⑴ (a+3)(a-3)
⑵ (2x+y)(2x-y)
⑶ (1+2c)(1-2c )
⑷ (2a+3b)(2a-3b)
请同学们自己计算一下:
例 2
= a -3
= (2x) - y
= 1 -(2c)
= (2a) - (3b)
= 4x - y
= 1- 4c
= 4a - 9b
= a -9
解:
练习: 运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
⑵ (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).
(4) (a+3b)(a-3b)
(5) (3+2a)(-3+2a)
能运用平方差公式计算的其他形式:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
计算
本节课你的收获是什么?
试用语言表述平方差公式 (a+b)(a b)=x2 b2。
应用平方差公式 时要注意一些什么?
两数和与这两数差的积,等于它们的平方差。
变成公式标准形式后,再用公式。
或提取两“ ”号中的“ ”号,
运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式;
要利用加法交换律,
对于不符合平方差公式标准形式者,
1判断
⑴.(m+3n)(m-3n)=m -3n ( )⑵.(- m+3n)(m-3n)=m -9n ( )⑶.(- m - 3n)(- m + 3n)=m -9n ( )⑷.(m-3n) = m -9n ( )
作业
1.(m+2n)(-2n+m) 2.(-2x-y) (2x-y)
3.(-2a+3b)(-2a+3b) 4.(x2+y2)(x2-y2)
2计算
3.下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a) C.(2a-3b)(3a+2b)
D.(a-b)(b-a) E.(x-2y)(2y+x) F.(-x+2y)(-x-2y)
G.(-2y-x)(x+2y) H.(-2b-5)(2b-5)
