12.3.2.3乘法公式的综合应用 课件(共15张PPT)
文档属性
| 名称 | 12.3.2.3乘法公式的综合应用 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 470.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 00:00:00 | ||
图片预览




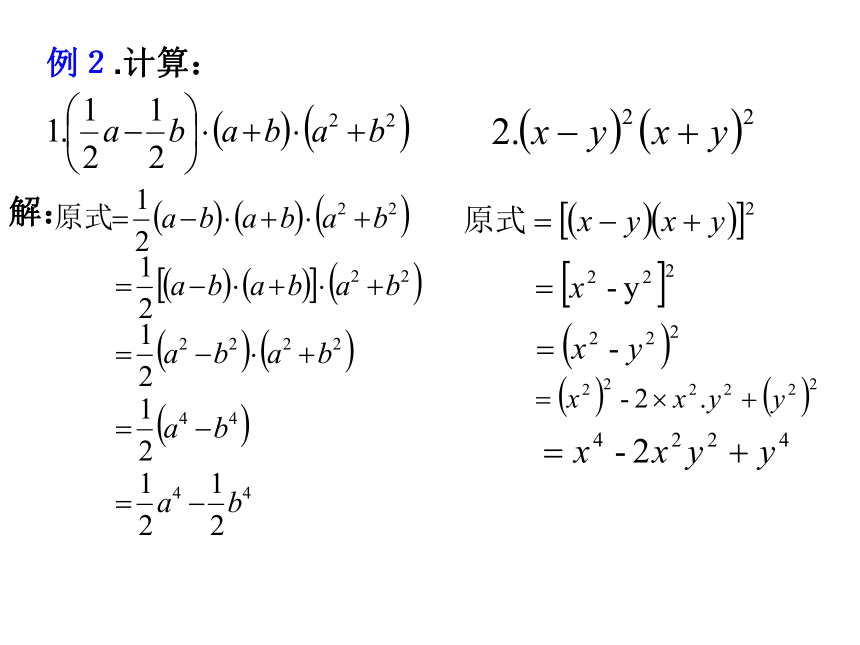
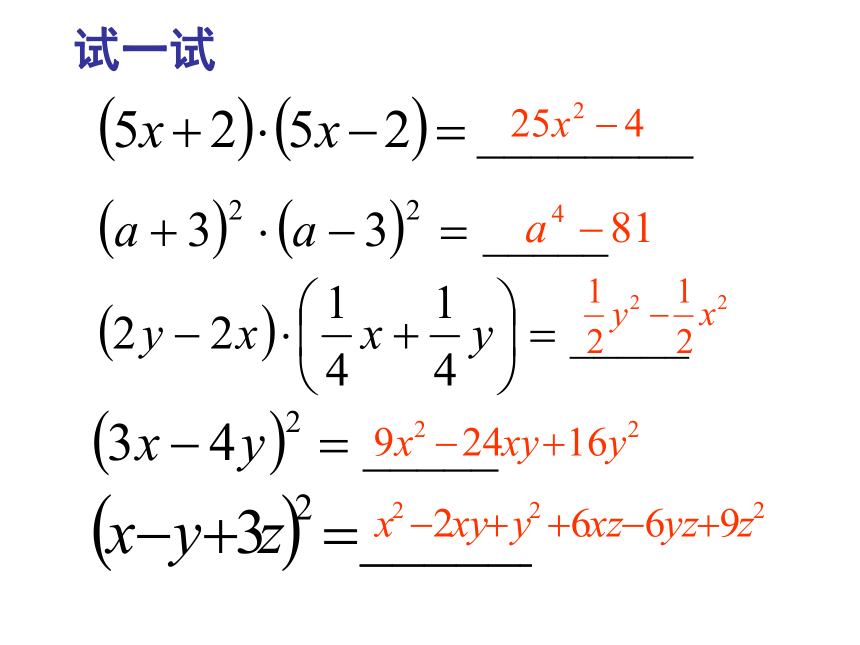

文档简介
(共15张PPT)
平方差公式:
完全平方公式:
有用的公式变形:
补充公式:
复习回顾
例1:用适当的方法计算下列各式:
(x-2y)(2y-x) (2) (2a+b+3)(2a+b-3)
(3) (a-2b+3)(a+2b-3)
解:
练习:利用公式计算下列各式。
(1)
(2)
(3)
(4)
你能用最少时间做完吗
例2.计算:
解:
试一试
1.两个多项式相乘,只要两项符号相同,另两项符号相反,就可以用平方差公式。
2.用平方差公式计算,直接用相同项的平方减去相反项的平方。最后运算结果有二项。
3.用完全平方公式时,应注意“首平方,尾平方,首尾乘积两倍在中央”,最后运算结果有三项。
5.公式中a,b可代表多项式,学会能够把一些项结合起来看作一项进行运算。
使用公式进行运算时要注意:
4.三数和的平方等于这三个数的分别平方加上它们两两相乘积的2倍.
例3、运用公式进行简便运算
(1)
(2)
解:原式=
(1)
(2)
解:原式=
做一做
解:
例4.
例5.若 试求
例6.若 (a+1)2+b2-8b+16=0,求 3(a-b)的值。
∴a = -1 , b = 4
∴3(a-b)=3(-1-4)=-15
解:∵ (a+1)2+b2-8b+16=0
归纳:如果一个代数式的和为0,应考虑将代数式转化为几个完全平方式相加的形式;再根据“几个非负数的和为0,每个均为0”求出未知数。
例7.
练习:已知a2+b2+4a-6b+13=0,求a2+b2的值
所以,三角形为正三角形 。
例8
1.用合适的方法计算
2.若a-b=2,a-c=1,则b-c=( )
4.已知a2+b2+2a-6b+10=0,求a与b的值
作 业
平方差公式:
完全平方公式:
有用的公式变形:
补充公式:
复习回顾
例1:用适当的方法计算下列各式:
(x-2y)(2y-x) (2) (2a+b+3)(2a+b-3)
(3) (a-2b+3)(a+2b-3)
解:
练习:利用公式计算下列各式。
(1)
(2)
(3)
(4)
你能用最少时间做完吗
例2.计算:
解:
试一试
1.两个多项式相乘,只要两项符号相同,另两项符号相反,就可以用平方差公式。
2.用平方差公式计算,直接用相同项的平方减去相反项的平方。最后运算结果有二项。
3.用完全平方公式时,应注意“首平方,尾平方,首尾乘积两倍在中央”,最后运算结果有三项。
5.公式中a,b可代表多项式,学会能够把一些项结合起来看作一项进行运算。
使用公式进行运算时要注意:
4.三数和的平方等于这三个数的分别平方加上它们两两相乘积的2倍.
例3、运用公式进行简便运算
(1)
(2)
解:原式=
(1)
(2)
解:原式=
做一做
解:
例4.
例5.若 试求
例6.若 (a+1)2+b2-8b+16=0,求 3(a-b)的值。
∴a = -1 , b = 4
∴3(a-b)=3(-1-4)=-15
解:∵ (a+1)2+b2-8b+16=0
归纳:如果一个代数式的和为0,应考虑将代数式转化为几个完全平方式相加的形式;再根据“几个非负数的和为0,每个均为0”求出未知数。
例7.
练习:已知a2+b2+4a-6b+13=0,求a2+b2的值
所以,三角形为正三角形 。
例8
1.用合适的方法计算
2.若a-b=2,a-c=1,则b-c=( )
4.已知a2+b2+2a-6b+10=0,求a与b的值
作 业
