12.5.1.2 因式分解(公式法) 课件(共31张PPT)
文档属性
| 名称 | 12.5.1.2 因式分解(公式法) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 20:20:34 | ||
图片预览










文档简介
(共31张PPT)
课前准备
请拿出你的课本、彩色笔和练习本等用品,还有你的激情和坐姿。
学而不思则罔 思而不探则空
12.5.1.1因式分解——公式法
第二课时
判断下列等式从左至右的变形是否因式分解
(1) x2-3x-1=x(x-3) -1
(2) (x-3)(x+2)=x2-x-6
(3) x2+1=x(x+ )
(4) a2-4ab+4b2=(a-2b)2
辨一辨
………(×)
………(×)
…………(×)
…(√)
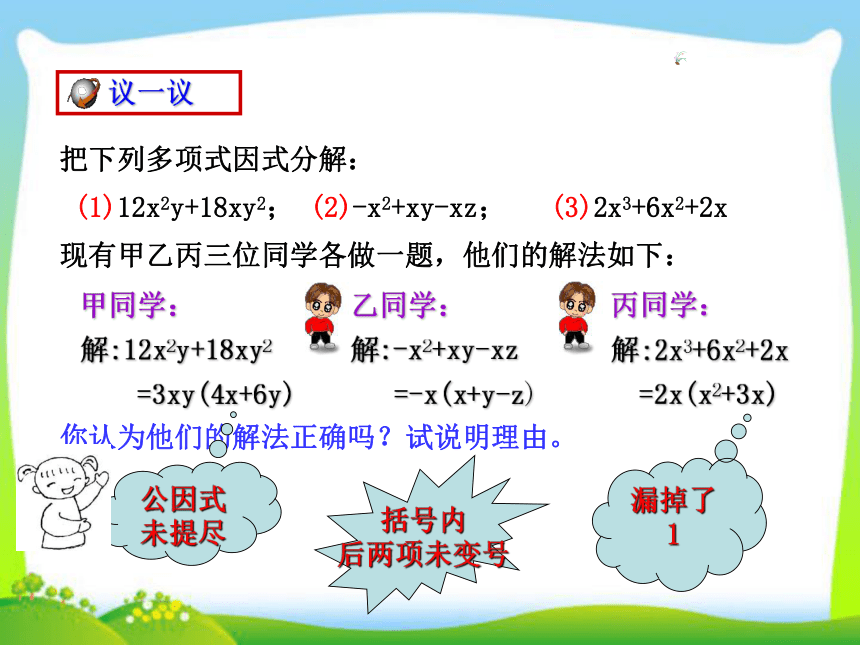
把下列多项式因式分解:
(1)12x2y+18xy2; (2)-x2+xy-xz; (3)2x3+6x2+2x
现有甲乙丙三位同学各做一题,他们的解法如下:
你认为他们的解法正确吗?试说明理由。
甲同学:
解:12x2y+18xy2
=3xy(4x+6y)
乙同学:
解:-x2+xy-xz
=-x(x+y-z)
丙同学:
解:2x3+6x2+2x
=2x(x2+3x)
括号内
后两项未变号
漏掉了1
议一议
公因式未提尽
用提公因式法分解因式:
8a3b2-12ab3c
(2)a(p-q)-4b(q-p)
做一做
=4ab2(2a2-3bc)
公因式既可以由单项式充当,也可以由多项式充当。
=(p-q)(a+4b)
1.什么叫因式分解?我们已学过什么因式分解的方法?
A、因式分解:把一个多项式化为几个整式的积的形式
回顾 & 思考
B、方法:提取公因式
2.因式分解与整式乘法有什么区别和联系?
B、区别和联系:因式分解是整式积的形式,整式乘法是和的形式;它们互为相反的变形。
3.我们学过哪些乘法公式?
A、平方差:(a+b)(a-b)=a2-b2
B、完全平方和:(a+b)2=a2+2ab+b2
C、完全平方差:(a-b)2=a2-2ab+b2
确定公因式的方法:三定,即定系数、定字母、定指数
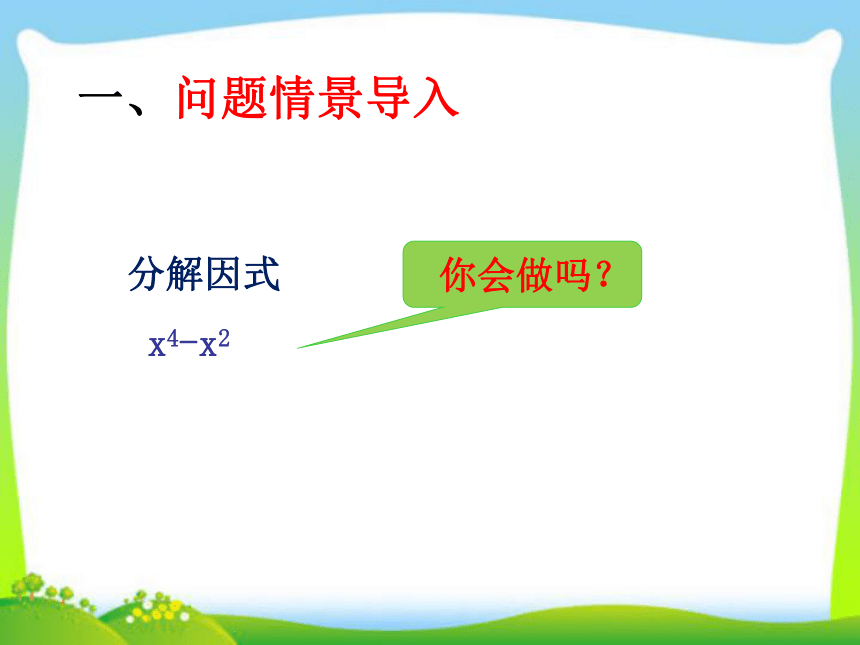
一、问题情景导入
分解因式
x4-x2
你会做吗?
1、(a+b)(a-b)=_______。
a2-b2
这个公式叫____________。
平方差公式
2、反过来,a2-b2=____________ 。
(a+b)(a-b)
从左边到右边的这个过程叫_________。
分解因式
3、因此,a2-b2=(a+b)(a-b)是因式分解中的一个公式。
从左边到右边的这个过程叫_________。
整式乘法
二、探究新知
运用公式法
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
逆用乘法公式把某些多项式进行因式分解。这种分解因式的方法叫做运用公式法。
乘法公式
因式分解
反过来
两个数的平方差,等于这两个数的和与这两个数的差的积。
①有两部分组成。
②两部分的符号相反。
③两部分都可写成数(或式)的平方的形式。
运用平方差公式分解有哪些条件?
我们称这种分解因式方法叫运用平方差公式分解因式
想想:
下列二项式哪些可以用平方差公式分解因式?
用平方差公式分解因式的关键:在于把两项式如何化成的两个数平方差的形式。
⑴ x2 + y2 ⑵ 1-m2
⑶ -a2-b2 ⑷ x2-9+x
⑸ -9+16x2 ⑹ x2-9y2
⑺ 4x2-9y ⑻ 36x2-(-y2)
⑼ x4-1
不行
行
不行
不行
行
行
行
不行
行
例1.把下列各式分解因式
⑴16a - 1 ⑵4x - m n
⑶-x +y ⑷–9x + 4
解:⑴原式=(4a) - 1
=(4a+1)(4a-1)
⑵原式=(2x) - (mn)
=(2x+mn)(2x-mn)
⑶原式=y - x
=(y+x)(y-x)
⑷原式=4 – 9x
=2 - (3x)
=(2+3x)(2-3x)
例2.把下列各式分解因式
(1)原式=(a2+9b2)(a2-9b2)
=(a2+9b2)(a+3b)(a-3b)
(2)原式=2a(4a2-1)
=2a(2a+1)(2a-1)
(3)原式=3abc(9a2-b2)
=3abc(3a+b)(3a-b)
解:
例3.把下列各式因式分解
⑴( x+z ) -( y+z ) ⑵4( a+b) -25(a-c)
⑶ (x+y+z) -(x-y -z )
解:1.原式=[(x+z)+(y+z)][(x+z)-(y+z)]
=(x+y+2z)(x-y)
2.原式=[2(a+b)] -[5(a-c)]
=[2(a+b)+ 5(a-c)][2(a+b)- 5(a-c)]
=(7a+2b-5c)(-3a+2b+5c)
3.原式=[(x+y+z)+(x-y-z)]×[(x+y+z)- (x-y-z)]
=2 ( 2 y + 2 z)
=4 ( y + z )
注意:
1.在利用平方差公式因式分解时,关键是找出进行平方差的两数是何数的平方,再把它们的和与差相乘。
2.若多项式中有公因式,应先提取公因式,然后再进一步利用乘法公式进行分解因式。
3.分解因式要彻底,要分解到结果的每个因式都不能再分解为止。
4.公式中的a,b可以是单独的数字、字母,也可以是单项式、多项式。
即:能写成( )2-( )2的式子,可以用平方差公式分解因式。
练习:把下列各式分解因式:
(5)( x + z ) - ( y + z )
我们可以通过以上公式把“完全平方式”分解因式,称为:运用完全平方公式分解因式。
完全平方式的特点:
1.必须是三项式
2.有两个“平方”项,且符号相同;
3.第三项是两平方项底数积的2倍或-2倍。
想一想:
下列多项式是完全平方式的有:
(1)a2-4a+4 (2)1+4a2
(3)4b2+4b-1 (4)a2+ab+b2
(5)a2-b2+2ab (6)x2+2xy+4y2
(7)-4a2+12ab-9b2 (8)a4+4ab+4b4
(1)(7)
练一练:按照完全平方公式填空:
(1)
x2+14x+49
解:
例4.分解因式
(2)25x2+10x+1
原式=(5x)2+2×5x×1+12
=(5x+1)2
原式=(3a)2-2×3a×b+b2
=(3a-b)2
(4)
-x2-4y2+4xy
分解因式:
a2-4ab+4b2-1=___________________。
(a-2b+1)(a-2b-1)
【点拨】a2-4ab+4b2-1
=(a-2b)2-1
=(a-2b+1)(a-2b-1)。
巩固练习
例5.分解因式
解:
练习:分解因式
ax2+2a2x+a3
-3ax2+6axy-3ay2
例6.分解因式
(1)(a+1)2-2(a2-1) +(a-1)2
解:
练习:
1.运用完全平方公式分解要把握完全平方式特征;
2.将平方差公式与完全平方公式相区别;
3.有公因式要先提取公因式,再用公式法分解;
4.因式分解到不能分解为止;
5.分解结果如若是积的幂的形式必须写成幂的积的形式。
注意:
例7.用简便方法计算:
练习:
解:
例7.若n是整数,试说明(2n+1)2-(2n-1)2是8的倍数。
解:原式=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=(2n+1+2n-1)(2n+1-2n+1)
=4n.2
=8n
∴ (2n+1)2-(2n-1)2是8的倍数。
公式法
因式分解
公式
平方差公式:a2-b2=(a+b)(a-b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止
完全平方公式:a2±2ab+b2=(a±b)2
课堂总结
1.下列多项式可以用平方差公式分解因式的( )
A.4x2+y2 B.-0.49x2+y2 C.-4x2-y2 D.9+(-y)2
2.下列各式中,能用完全平方公式分解的是( )
A.a2+b2+ab B.a2+2ab-b2 C.a2-ab+2b2 D.-2ab+a2+b2
3.下列各式中,不能用完全平方公式分解的是( )
A.x2+y2-2xy B.x2+4xy+4y2 C.a2-ab+b2 D.-2ab+a2+b2
4.如果100x2+kxy+y2=(10x-y)2,那么k的值是( )
5.如果x2+mxy+9y2是完全平方式,那么m的值为( )
(9)18-2b
6.分解因式
(7)
(8)
课后作业
补充练习
请用学过知识来解下列问题:
(1)已知x2+y2-8x+12y+52=0
求(x+y)2的值;
(2)求x2+8x+7的最小值。
(2)解:x2+8x+7=(x2+8x+16)-16+7=(x+4)2-9。因为(x+4)2≥0,所以(x+4)2-9≥-9。所以x2+8x+7的最小值是-9。
谢谢指导
课前准备
请拿出你的课本、彩色笔和练习本等用品,还有你的激情和坐姿。
学而不思则罔 思而不探则空
12.5.1.1因式分解——公式法
第二课时
判断下列等式从左至右的变形是否因式分解
(1) x2-3x-1=x(x-3) -1
(2) (x-3)(x+2)=x2-x-6
(3) x2+1=x(x+ )
(4) a2-4ab+4b2=(a-2b)2
辨一辨
………(×)
………(×)
…………(×)
…(√)
把下列多项式因式分解:
(1)12x2y+18xy2; (2)-x2+xy-xz; (3)2x3+6x2+2x
现有甲乙丙三位同学各做一题,他们的解法如下:
你认为他们的解法正确吗?试说明理由。
甲同学:
解:12x2y+18xy2
=3xy(4x+6y)
乙同学:
解:-x2+xy-xz
=-x(x+y-z)
丙同学:
解:2x3+6x2+2x
=2x(x2+3x)
括号内
后两项未变号
漏掉了1
议一议
公因式未提尽
用提公因式法分解因式:
8a3b2-12ab3c
(2)a(p-q)-4b(q-p)
做一做
=4ab2(2a2-3bc)
公因式既可以由单项式充当,也可以由多项式充当。
=(p-q)(a+4b)
1.什么叫因式分解?我们已学过什么因式分解的方法?
A、因式分解:把一个多项式化为几个整式的积的形式
回顾 & 思考
B、方法:提取公因式
2.因式分解与整式乘法有什么区别和联系?
B、区别和联系:因式分解是整式积的形式,整式乘法是和的形式;它们互为相反的变形。
3.我们学过哪些乘法公式?
A、平方差:(a+b)(a-b)=a2-b2
B、完全平方和:(a+b)2=a2+2ab+b2
C、完全平方差:(a-b)2=a2-2ab+b2
确定公因式的方法:三定,即定系数、定字母、定指数
一、问题情景导入
分解因式
x4-x2
你会做吗?
1、(a+b)(a-b)=_______。
a2-b2
这个公式叫____________。
平方差公式
2、反过来,a2-b2=____________ 。
(a+b)(a-b)
从左边到右边的这个过程叫_________。
分解因式
3、因此,a2-b2=(a+b)(a-b)是因式分解中的一个公式。
从左边到右边的这个过程叫_________。
整式乘法
二、探究新知
运用公式法
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
逆用乘法公式把某些多项式进行因式分解。这种分解因式的方法叫做运用公式法。
乘法公式
因式分解
反过来
两个数的平方差,等于这两个数的和与这两个数的差的积。
①有两部分组成。
②两部分的符号相反。
③两部分都可写成数(或式)的平方的形式。
运用平方差公式分解有哪些条件?
我们称这种分解因式方法叫运用平方差公式分解因式
想想:
下列二项式哪些可以用平方差公式分解因式?
用平方差公式分解因式的关键:在于把两项式如何化成的两个数平方差的形式。
⑴ x2 + y2 ⑵ 1-m2
⑶ -a2-b2 ⑷ x2-9+x
⑸ -9+16x2 ⑹ x2-9y2
⑺ 4x2-9y ⑻ 36x2-(-y2)
⑼ x4-1
不行
行
不行
不行
行
行
行
不行
行
例1.把下列各式分解因式
⑴16a - 1 ⑵4x - m n
⑶-x +y ⑷–9x + 4
解:⑴原式=(4a) - 1
=(4a+1)(4a-1)
⑵原式=(2x) - (mn)
=(2x+mn)(2x-mn)
⑶原式=y - x
=(y+x)(y-x)
⑷原式=4 – 9x
=2 - (3x)
=(2+3x)(2-3x)
例2.把下列各式分解因式
(1)原式=(a2+9b2)(a2-9b2)
=(a2+9b2)(a+3b)(a-3b)
(2)原式=2a(4a2-1)
=2a(2a+1)(2a-1)
(3)原式=3abc(9a2-b2)
=3abc(3a+b)(3a-b)
解:
例3.把下列各式因式分解
⑴( x+z ) -( y+z ) ⑵4( a+b) -25(a-c)
⑶ (x+y+z) -(x-y -z )
解:1.原式=[(x+z)+(y+z)][(x+z)-(y+z)]
=(x+y+2z)(x-y)
2.原式=[2(a+b)] -[5(a-c)]
=[2(a+b)+ 5(a-c)][2(a+b)- 5(a-c)]
=(7a+2b-5c)(-3a+2b+5c)
3.原式=[(x+y+z)+(x-y-z)]×[(x+y+z)- (x-y-z)]
=2 ( 2 y + 2 z)
=4 ( y + z )
注意:
1.在利用平方差公式因式分解时,关键是找出进行平方差的两数是何数的平方,再把它们的和与差相乘。
2.若多项式中有公因式,应先提取公因式,然后再进一步利用乘法公式进行分解因式。
3.分解因式要彻底,要分解到结果的每个因式都不能再分解为止。
4.公式中的a,b可以是单独的数字、字母,也可以是单项式、多项式。
即:能写成( )2-( )2的式子,可以用平方差公式分解因式。
练习:把下列各式分解因式:
(5)( x + z ) - ( y + z )
我们可以通过以上公式把“完全平方式”分解因式,称为:运用完全平方公式分解因式。
完全平方式的特点:
1.必须是三项式
2.有两个“平方”项,且符号相同;
3.第三项是两平方项底数积的2倍或-2倍。
想一想:
下列多项式是完全平方式的有:
(1)a2-4a+4 (2)1+4a2
(3)4b2+4b-1 (4)a2+ab+b2
(5)a2-b2+2ab (6)x2+2xy+4y2
(7)-4a2+12ab-9b2 (8)a4+4ab+4b4
(1)(7)
练一练:按照完全平方公式填空:
(1)
x2+14x+49
解:
例4.分解因式
(2)25x2+10x+1
原式=(5x)2+2×5x×1+12
=(5x+1)2
原式=(3a)2-2×3a×b+b2
=(3a-b)2
(4)
-x2-4y2+4xy
分解因式:
a2-4ab+4b2-1=___________________。
(a-2b+1)(a-2b-1)
【点拨】a2-4ab+4b2-1
=(a-2b)2-1
=(a-2b+1)(a-2b-1)。
巩固练习
例5.分解因式
解:
练习:分解因式
ax2+2a2x+a3
-3ax2+6axy-3ay2
例6.分解因式
(1)(a+1)2-2(a2-1) +(a-1)2
解:
练习:
1.运用完全平方公式分解要把握完全平方式特征;
2.将平方差公式与完全平方公式相区别;
3.有公因式要先提取公因式,再用公式法分解;
4.因式分解到不能分解为止;
5.分解结果如若是积的幂的形式必须写成幂的积的形式。
注意:
例7.用简便方法计算:
练习:
解:
例7.若n是整数,试说明(2n+1)2-(2n-1)2是8的倍数。
解:原式=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=(2n+1+2n-1)(2n+1-2n+1)
=4n.2
=8n
∴ (2n+1)2-(2n-1)2是8的倍数。
公式法
因式分解
公式
平方差公式:a2-b2=(a+b)(a-b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止
完全平方公式:a2±2ab+b2=(a±b)2
课堂总结
1.下列多项式可以用平方差公式分解因式的( )
A.4x2+y2 B.-0.49x2+y2 C.-4x2-y2 D.9+(-y)2
2.下列各式中,能用完全平方公式分解的是( )
A.a2+b2+ab B.a2+2ab-b2 C.a2-ab+2b2 D.-2ab+a2+b2
3.下列各式中,不能用完全平方公式分解的是( )
A.x2+y2-2xy B.x2+4xy+4y2 C.a2-ab+b2 D.-2ab+a2+b2
4.如果100x2+kxy+y2=(10x-y)2,那么k的值是( )
5.如果x2+mxy+9y2是完全平方式,那么m的值为( )
(9)18-2b
6.分解因式
(7)
(8)
课后作业
补充练习
请用学过知识来解下列问题:
(1)已知x2+y2-8x+12y+52=0
求(x+y)2的值;
(2)求x2+8x+7的最小值。
(2)解:x2+8x+7=(x2+8x+16)-16+7=(x+4)2-9。因为(x+4)2≥0,所以(x+4)2-9≥-9。所以x2+8x+7的最小值是-9。
谢谢指导
