13.2.3.1三角形全等判定边角边(SAS) 课件(共34张PPT)
文档属性
| 名称 | 13.2.3.1三角形全等判定边角边(SAS) 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 17:25:03 | ||
图片预览










文档简介
(共34张PPT)
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
第13章 全等三角形
13.2.3 全等三角形判定
边角边(SAS)
华师版数学八年级上册
2、全等三角形的判定条件是什么?
若两个三角形的三条边与三个角都分别对应相等,那么这两个三角形一定可以互相重合,即全等。
1、全等三角形的定义是什么?
能够完全重合的两个三角形是全等三角形
知识回顾
若△AOC≌△BOD,
对应边: AC= ,
AO= ,
CO= ;
对应角: ∠A= ,
∠C= ,
∠AOC= 。
A
B
O
C
D
温故知新:全等三角形的性质
BD
BO
DO
∠B
∠D
∠BOD
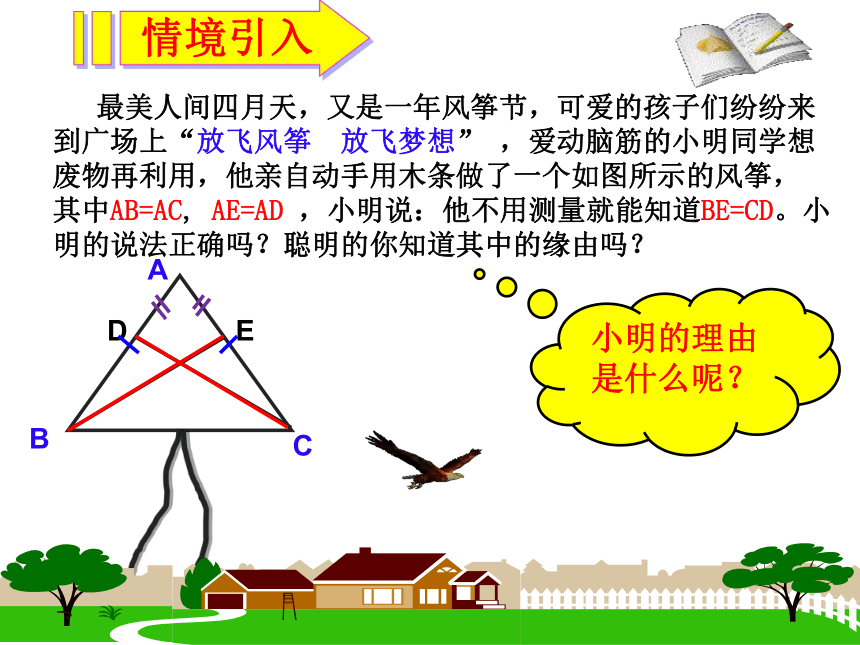
最美人间四月天,又是一年风筝节,可爱的孩子们纷纷来到广场上“放飞风筝 放飞梦想” ,爱动脑筋的小明同学想废物再利用,他亲自动手用木条做了一个如图所示的风筝, 其中AB=AC, AE=AD ,小明说:他不用测量就能知道BE=CD。小明的说法正确吗?聪明的你知道其中的缘由吗?
小明的理由是什么呢?
A
B
C
D
E
情境引入
三边三角
六个元素
一个元素
两个元素
三个元素
一边
一角
两边
一边
一角
两角
两边
一角
两角
一边
三边
三角
思考:如果两个三角形有相等的部分(边或角),那么有几种可能的情况?这两个三角形一定全等吗?
两边一角又会有哪几种情况?
请同学们探讨一下!
(2)边边角
(1)边角边
夹角
“边角边”是否能够判断两个三角形全等呢?下面我们来探讨一下!
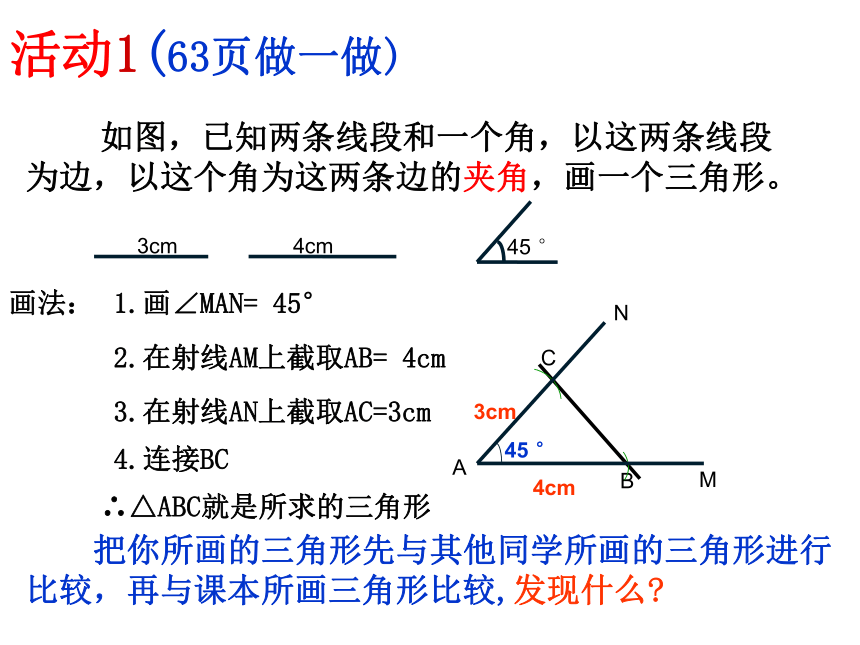
如图,已知两条线段和一个角,以这两条线段为边,以这个角为这两条边的夹角,画一个三角形。
3cm
4cm
画法:
1.画∠MAN= 45°
2.在射线AM上截取AB= 4cm
3.在射线AN上截取AC=3cm
4.连接BC
∴△ABC就是所求的三角形
把你所画的三角形先与其他同学所画的三角形进行比较,再与课本所画三角形比较,发现什么
B
4cm
C
3cm
45 °
N
A
M
45 °
活动1(63页做一做)
三角形全等的判定1:
1.基本事实:
2.图形语言:
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。
简记为SAS(或边角边)
A
B
C
A
B
C
3.几何语言:
形成结论
边角边公理
几何语言
B
C
A
B '
C '
A '
B
C
A
在△ABC和△A'B'C'中
①指明对象
②书写条件
③得出结论
AB=A'B'
∠B=∠B'
BC=B'C'
∴△ABC≌△A'B'C'(SAS)
边角边公理书写模板
在△※※※和△○○○中:
= (填写边)
= (填写角)
= (填写边)∴△※※※ ≌△○○○(SAS)
书写格式:1.指出是哪两个三角形;
2.按边角边顺序写出三个相等条件(注意顶点间的对应);
3.写出全等结论,并注明全等的依据。
例1:如图19.2.4,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD。
证明:
∵ AD平分∠BAC
∴ ∠BAD=∠CAD
在△ABD与△ACD中:
∴△ABD≌△ACD(SAS)
AB=AC (已知)
∠BAD=∠CAD (已证)
AD=AD(公共边)
注意:图形中隐含了公共边这一相等条件。
典例讲解
证明:在△ AEC和 中
例2、 如图,在△AEC和△ ADB中,已知AE=AD,AC=AB.
请说明△ AEC ≌ △ ADB的理由.
AE =____(已知)
= ( )
_____= AB ( )
∴ △_____≌△______( )
A
E
B
D
C
AD
AC
SAS
∠A
∠A
已知
AEC
ADB
典例讲解
叙述全等的三个条件
找准两个△
得出全等结论,并写出全等理由
公共角
“公共角”是证全等的一个隐含条件哟。
△ADB
例3:已知:如图,AD∥BC,AD=CB。
求证: △ADC≌△CBA
A
B
C
D
1
2
证明:∵AD∥BC
∴ ∠1=∠2
( )
在△ADC和△CBA中:
AD=CB(已知)
∠1=∠2(已证)
AC=CA(公共边)
∴ △ADC≌△CBA(SAS)
两直线平行,内错角相等
练习:课本65页练习1-2。
注意:当证明两个三角形全等题中条件不充足时,应先根据已知得出相关的相等条件.这里我们称“准备条件”.这是以后经常会碰到的。
典例讲解
边角边的适用情况:
要证两个三角形全等,若已知两边相等,
可考虑证两边的夹角相等.
证边相等的方法有:
①公共边;
②等线段加(减)等线段其和(差)相等,即等式性质;
③由中点得到线段相等;
④同等于第三条线段的两线段相等,即等量代换;
⑤全等三角形的对应边相
方法指导
(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)仍相等;
(3)同角或等角的余(补)角相等;
(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;
(6)直角都相等;
(7)全等三角形对应角相等;
(8)第三角代换,即等量代换等.
找相等角方法有:
巩固练习
1.在下列图中找出全等三角形:
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
8 cm
5 cm
Ⅱ
30
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
探讨:
“边边角”是否能够判断两个三角形全等呢?
边边角
A
B
M
C
D
A
B
C
A
B
D
4cm
3cm
3cm
步骤:
1、画一线段AB,使它等于10cm ;
2、画∠ BAM= 45° ;
3、以B为圆心, 6cm长为半径画弧,
交AM于点C ;
4、连结CB 。
△ABC即为所求。
3cm
4cm
45°
剪一个三角形,使它的两边长分别为3cm、4cm,且3cm所对的角为45°,情况又怎样?
结论:
两边及其一边所对的角相等,两个三角形不一定全等。所以,边边角不能作为判断全等的依据。
活动2(65页做一做)
1、当两个三角形的两条边及其夹角分别对应相等时,两个三角形一定全等。(SAS)
2、当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形未必一定全等。(SSA)
两角一边呢
归纳:
A
B
M
C
D
A
B
C
A
B
D
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长至D和E,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?为什么
C
A
E
D
B
实践运用:
解:可行,理由如下:
在△DCE和△ACB中
DC=AC (已知)
∠DCE=∠ACB(对顶角相等)
EC=BC (已知)
∴△DCE≌△ACB(SAS)
∴DE=AB
注意:图形中隐含了对顶角相等这一已知条件。
最美人间四月天,又是一年风筝节,可爱的孩子们纷纷到广场上“放飞风筝,放飞梦想”,爱动脑筋的小明同学想废物再利用,他亲自动手用木条做了一个如图所示的风筝,其中AB=AC, AE=AD ,小明说:不用测量就能知道BE=CD。小明的说法正确吗?
A
B
C
D
E
在△ABE和△ACD中:
AB=AC(已知)
∠A=∠A(公共角)
AE=AD(已知)
∴△ABE≌△ACD(SAS)
∴BE=CD(全等三角形对应边相等)
解:正确,理由如下:
梦想成真
1.注意隐含条件:公共角(边)
2.证明两条线段(角)相等可以证线段(角)所在三角形全等
感悟
情境引入
达标测评:
(4分钟自主解答,2分钟小组合作,共6分钟)
1.如图所示,已知AD∥BC,AD=BC,
要用“边角边”定理证明△ABC≌△CDA,
需要三个条件。这三个条件中,已具有
两个条件,一是 ,二是 ,
还需要一个条件是 。
2.如图所示,A、B、C、D在同一条
直线上,且AC=BD,∠CAE=∠DBF,
要使△ACE≌△BDF,则还需补充一
个条件是 。
F
E
D
C
B
A
AD=BC
AC=AC
∠DAC=∠BCA
AE=BF
1.探索并掌握基本事实(SAS):
2.用“边角边”证明两个三角形全等需注意什么?
⑴ 分类讨论的数学思想 ⑵ 合情推理的重要方法
⑶ 数学活动经验的积累
两边及其夹角分别相等的两个三角形全等。
3.数学素养:
⑴ 边角边中所出现的边与角必须是所证明的两个三角形中的元素;
⑵ 边角边中涉及的角必须是两边的夹角;
⑶ 证明两个三角形全等时若缺条件,要灵活根据其它已知条件推出所缺条件;
⑷ 要充分利用图形中的隐含条件,如公共边、公共角、对顶角等.
小结
作 业:
P79习题19.2 第 2、4题
P96复习题 第4题
课后作业:
1、已知:如图,AB=AC,AD = AE .
求证:△ABE≌△ACD.
B
E
A
C
D
2、如图:己知AD∥BC,AE=CF,AD=BC,
E、F都在直线AC上,试说明DE∥BF。
F
C
B
E
D
A
A
B
D
C
3、如图1:若AB=AC,则添加什么条件可得
△ABD≌△ACD
4、如图2:若AB=AD,∠1=∠2,则添加什么
条件可得△ABC≌△ADE
A
B
C
D
E
1
2
4、 如图,已知AD//BC , AD=BC,
求证:△ABC ≌ △CDA
A
D
B
C
E
F
AE=CF,
△AFD ≌ △CEB
B
C
A
D
E
F
7.如图,已知:AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2(已知),
∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质),
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(S.A.S.).
∴ ∠A=∠D(全等三角形的对应角相等).
1
A
2
C
B
D
E
选 做 题
8.如图1,AC=BD,∠CAB=∠DBA.
试问:AO与BO 相等吗?若相等,请说明理由。
图 1
O
A
B
C
D
选 做 题
2.如图2,已知M是AB的中点,MC=MD,∠1=∠2.
试问:AC与BD 相等吗?若相等,请说明理由。
1
C
D
2
图 2
A
M
B
3.如图3,△ABC中 ,AD⊥BC于D,AD=BD,DC=DE,∠C=50°.求∠EBD的度数。
图 3
E
A
B
C
D
9.【陕西中考】如图,点A、E、F、B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.10.小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流.
E
F
D
H
解:能.在△EDH和△FDH中 ,
ED=FD(已知),
∠EDH=∠FDH(已知),
DH=DH(公共边),
∴△EDH≌△FDH(S.A.S.).
∴EH=FH(全等三角形对应边相等).
11、已知:如图,AB=AC, AE=AD.
求证: △ABE≌△ACD
A
C
D
B
E
A
证明:在△ABE和△ACD中
∵ AB=AC(已知)
∠A=∠A(公共角)
AE= AD (已知)
∴ △ABE≌△ACD(SAS)
试一试,你能行
12、变式1:已知:如图,AB=AC,AE=AD
求证:(1)∠B=∠C
(2) BE=CD
时间3分钟
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
第13章 全等三角形
13.2.3 全等三角形判定
边角边(SAS)
华师版数学八年级上册
2、全等三角形的判定条件是什么?
若两个三角形的三条边与三个角都分别对应相等,那么这两个三角形一定可以互相重合,即全等。
1、全等三角形的定义是什么?
能够完全重合的两个三角形是全等三角形
知识回顾
若△AOC≌△BOD,
对应边: AC= ,
AO= ,
CO= ;
对应角: ∠A= ,
∠C= ,
∠AOC= 。
A
B
O
C
D
温故知新:全等三角形的性质
BD
BO
DO
∠B
∠D
∠BOD
最美人间四月天,又是一年风筝节,可爱的孩子们纷纷来到广场上“放飞风筝 放飞梦想” ,爱动脑筋的小明同学想废物再利用,他亲自动手用木条做了一个如图所示的风筝, 其中AB=AC, AE=AD ,小明说:他不用测量就能知道BE=CD。小明的说法正确吗?聪明的你知道其中的缘由吗?
小明的理由是什么呢?
A
B
C
D
E
情境引入
三边三角
六个元素
一个元素
两个元素
三个元素
一边
一角
两边
一边
一角
两角
两边
一角
两角
一边
三边
三角
思考:如果两个三角形有相等的部分(边或角),那么有几种可能的情况?这两个三角形一定全等吗?
两边一角又会有哪几种情况?
请同学们探讨一下!
(2)边边角
(1)边角边
夹角
“边角边”是否能够判断两个三角形全等呢?下面我们来探讨一下!
如图,已知两条线段和一个角,以这两条线段为边,以这个角为这两条边的夹角,画一个三角形。
3cm
4cm
画法:
1.画∠MAN= 45°
2.在射线AM上截取AB= 4cm
3.在射线AN上截取AC=3cm
4.连接BC
∴△ABC就是所求的三角形
把你所画的三角形先与其他同学所画的三角形进行比较,再与课本所画三角形比较,发现什么
B
4cm
C
3cm
45 °
N
A
M
45 °
活动1(63页做一做)
三角形全等的判定1:
1.基本事实:
2.图形语言:
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。
简记为SAS(或边角边)
A
B
C
A
B
C
3.几何语言:
形成结论
边角边公理
几何语言
B
C
A
B '
C '
A '
B
C
A
在△ABC和△A'B'C'中
①指明对象
②书写条件
③得出结论
AB=A'B'
∠B=∠B'
BC=B'C'
∴△ABC≌△A'B'C'(SAS)
边角边公理书写模板
在△※※※和△○○○中:
= (填写边)
= (填写角)
= (填写边)∴△※※※ ≌△○○○(SAS)
书写格式:1.指出是哪两个三角形;
2.按边角边顺序写出三个相等条件(注意顶点间的对应);
3.写出全等结论,并注明全等的依据。
例1:如图19.2.4,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD。
证明:
∵ AD平分∠BAC
∴ ∠BAD=∠CAD
在△ABD与△ACD中:
∴△ABD≌△ACD(SAS)
AB=AC (已知)
∠BAD=∠CAD (已证)
AD=AD(公共边)
注意:图形中隐含了公共边这一相等条件。
典例讲解
证明:在△ AEC和 中
例2、 如图,在△AEC和△ ADB中,已知AE=AD,AC=AB.
请说明△ AEC ≌ △ ADB的理由.
AE =____(已知)
= ( )
_____= AB ( )
∴ △_____≌△______( )
A
E
B
D
C
AD
AC
SAS
∠A
∠A
已知
AEC
ADB
典例讲解
叙述全等的三个条件
找准两个△
得出全等结论,并写出全等理由
公共角
“公共角”是证全等的一个隐含条件哟。
△ADB
例3:已知:如图,AD∥BC,AD=CB。
求证: △ADC≌△CBA
A
B
C
D
1
2
证明:∵AD∥BC
∴ ∠1=∠2
( )
在△ADC和△CBA中:
AD=CB(已知)
∠1=∠2(已证)
AC=CA(公共边)
∴ △ADC≌△CBA(SAS)
两直线平行,内错角相等
练习:课本65页练习1-2。
注意:当证明两个三角形全等题中条件不充足时,应先根据已知得出相关的相等条件.这里我们称“准备条件”.这是以后经常会碰到的。
典例讲解
边角边的适用情况:
要证两个三角形全等,若已知两边相等,
可考虑证两边的夹角相等.
证边相等的方法有:
①公共边;
②等线段加(减)等线段其和(差)相等,即等式性质;
③由中点得到线段相等;
④同等于第三条线段的两线段相等,即等量代换;
⑤全等三角形的对应边相
方法指导
(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)仍相等;
(3)同角或等角的余(补)角相等;
(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;
(6)直角都相等;
(7)全等三角形对应角相等;
(8)第三角代换,即等量代换等.
找相等角方法有:
巩固练习
1.在下列图中找出全等三角形:
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
8 cm
5 cm
Ⅱ
30
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
探讨:
“边边角”是否能够判断两个三角形全等呢?
边边角
A
B
M
C
D
A
B
C
A
B
D
4cm
3cm
3cm
步骤:
1、画一线段AB,使它等于10cm ;
2、画∠ BAM= 45° ;
3、以B为圆心, 6cm长为半径画弧,
交AM于点C ;
4、连结CB 。
△ABC即为所求。
3cm
4cm
45°
剪一个三角形,使它的两边长分别为3cm、4cm,且3cm所对的角为45°,情况又怎样?
结论:
两边及其一边所对的角相等,两个三角形不一定全等。所以,边边角不能作为判断全等的依据。
活动2(65页做一做)
1、当两个三角形的两条边及其夹角分别对应相等时,两个三角形一定全等。(SAS)
2、当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形未必一定全等。(SSA)
两角一边呢
归纳:
A
B
M
C
D
A
B
C
A
B
D
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长至D和E,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?为什么
C
A
E
D
B
实践运用:
解:可行,理由如下:
在△DCE和△ACB中
DC=AC (已知)
∠DCE=∠ACB(对顶角相等)
EC=BC (已知)
∴△DCE≌△ACB(SAS)
∴DE=AB
注意:图形中隐含了对顶角相等这一已知条件。
最美人间四月天,又是一年风筝节,可爱的孩子们纷纷到广场上“放飞风筝,放飞梦想”,爱动脑筋的小明同学想废物再利用,他亲自动手用木条做了一个如图所示的风筝,其中AB=AC, AE=AD ,小明说:不用测量就能知道BE=CD。小明的说法正确吗?
A
B
C
D
E
在△ABE和△ACD中:
AB=AC(已知)
∠A=∠A(公共角)
AE=AD(已知)
∴△ABE≌△ACD(SAS)
∴BE=CD(全等三角形对应边相等)
解:正确,理由如下:
梦想成真
1.注意隐含条件:公共角(边)
2.证明两条线段(角)相等可以证线段(角)所在三角形全等
感悟
情境引入
达标测评:
(4分钟自主解答,2分钟小组合作,共6分钟)
1.如图所示,已知AD∥BC,AD=BC,
要用“边角边”定理证明△ABC≌△CDA,
需要三个条件。这三个条件中,已具有
两个条件,一是 ,二是 ,
还需要一个条件是 。
2.如图所示,A、B、C、D在同一条
直线上,且AC=BD,∠CAE=∠DBF,
要使△ACE≌△BDF,则还需补充一
个条件是 。
F
E
D
C
B
A
AD=BC
AC=AC
∠DAC=∠BCA
AE=BF
1.探索并掌握基本事实(SAS):
2.用“边角边”证明两个三角形全等需注意什么?
⑴ 分类讨论的数学思想 ⑵ 合情推理的重要方法
⑶ 数学活动经验的积累
两边及其夹角分别相等的两个三角形全等。
3.数学素养:
⑴ 边角边中所出现的边与角必须是所证明的两个三角形中的元素;
⑵ 边角边中涉及的角必须是两边的夹角;
⑶ 证明两个三角形全等时若缺条件,要灵活根据其它已知条件推出所缺条件;
⑷ 要充分利用图形中的隐含条件,如公共边、公共角、对顶角等.
小结
作 业:
P79习题19.2 第 2、4题
P96复习题 第4题
课后作业:
1、已知:如图,AB=AC,AD = AE .
求证:△ABE≌△ACD.
B
E
A
C
D
2、如图:己知AD∥BC,AE=CF,AD=BC,
E、F都在直线AC上,试说明DE∥BF。
F
C
B
E
D
A
A
B
D
C
3、如图1:若AB=AC,则添加什么条件可得
△ABD≌△ACD
4、如图2:若AB=AD,∠1=∠2,则添加什么
条件可得△ABC≌△ADE
A
B
C
D
E
1
2
4、 如图,已知AD//BC , AD=BC,
求证:△ABC ≌ △CDA
A
D
B
C
E
F
AE=CF,
△AFD ≌ △CEB
B
C
A
D
E
F
7.如图,已知:AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2(已知),
∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质),
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(S.A.S.).
∴ ∠A=∠D(全等三角形的对应角相等).
1
A
2
C
B
D
E
选 做 题
8.如图1,AC=BD,∠CAB=∠DBA.
试问:AO与BO 相等吗?若相等,请说明理由。
图 1
O
A
B
C
D
选 做 题
2.如图2,已知M是AB的中点,MC=MD,∠1=∠2.
试问:AC与BD 相等吗?若相等,请说明理由。
1
C
D
2
图 2
A
M
B
3.如图3,△ABC中 ,AD⊥BC于D,AD=BD,DC=DE,∠C=50°.求∠EBD的度数。
图 3
E
A
B
C
D
9.【陕西中考】如图,点A、E、F、B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.10.小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流.
E
F
D
H
解:能.在△EDH和△FDH中 ,
ED=FD(已知),
∠EDH=∠FDH(已知),
DH=DH(公共边),
∴△EDH≌△FDH(S.A.S.).
∴EH=FH(全等三角形对应边相等).
11、已知:如图,AB=AC, AE=AD.
求证: △ABE≌△ACD
A
C
D
B
E
A
证明:在△ABE和△ACD中
∵ AB=AC(已知)
∠A=∠A(公共角)
AE= AD (已知)
∴ △ABE≌△ACD(SAS)
试一试,你能行
12、变式1:已知:如图,AB=AC,AE=AD
求证:(1)∠B=∠C
(2) BE=CD
时间3分钟
