13.2.3.3三角形全等判定角角边(AAS)
文档属性
| 名称 | 13.2.3.3三角形全等判定角角边(AAS) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 17:40:10 | ||
图片预览




文档简介
(共22张PPT)
华师大版 八年级 上册
03
全等三角形判定——角角边(AAS)
复习提问:
全等三角形的判定方法:
1、图形变换(翻折、平移、旋转)
3、判定1边角边(SAS)
2、定义(六个元素)
4、判定2角边角(ASA)
复习提问:
几何语言:
E
F
A
B
C
D
AC=DF
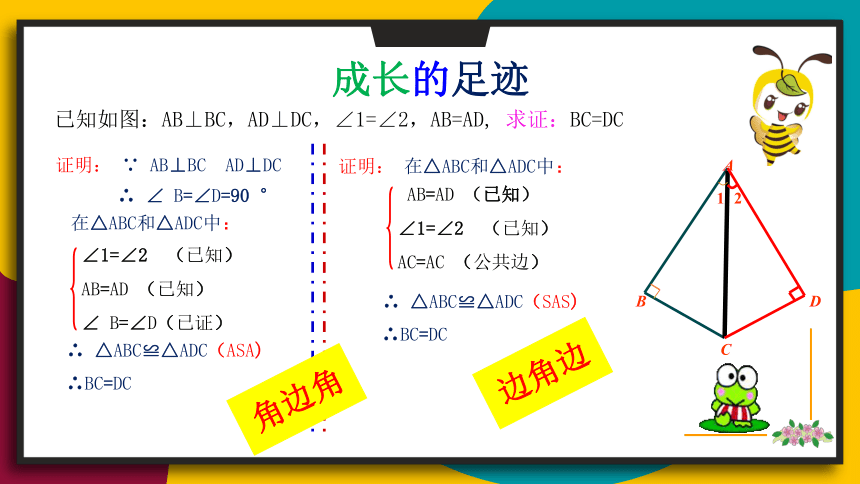
成长的足迹
已知如图:AB⊥BC,AD⊥DC,∠1=∠2,AB=AD, 求证:BC=DC
A
C
D
B
1
2
证明: ∵ AB⊥BC AD⊥DC
∴ ∠ B=∠D=90 °
在△ABC和△ADC中:
∠1=∠2 (已知)
AB=AD (已知)
∠ B=∠D(已证)
∴ △ABC≌△ADC(ASA)
∴BC=DC
证明: 在△ABC和△ADC中:
AB=AD (已知)
∠1=∠2 (已知)
AC=AC (公共边)
∴ △ABC≌△ADC(SAS)
∴BC=DC
角边角
边角边
思考:如图:如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
已知:∠A=∠A′,∠B=∠B′,AC=A′C′
求证: △ABC≌△A′B′C′
证明:∵∠A=∠A′,∠B=∠B′
且∠A+∠B+∠C=180°
∠A′+∠B′+∠C′=180°
∴ ∠C=∠C′
在△ABC和△A′B′C′中
∠A=∠A′
AC=A′C′
∠C=∠C′
∴△ABC≌△A′B′C′(ASA)
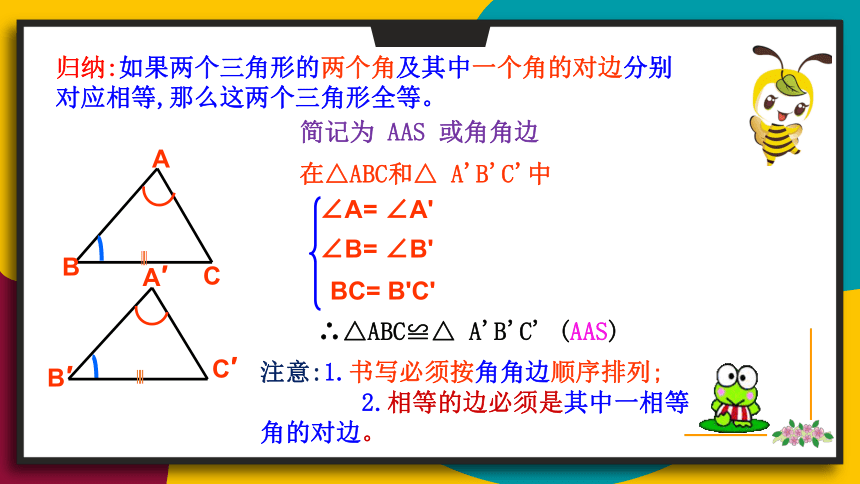
归纳:如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等。
在△ABC和△ A'B'C'中
简记为 AAS 或角角边
∴△ABC≌△ A'B'C' (AAS)
∠A= ∠A'
BC= B'C'
∠B= ∠B'
A
C
B
A′
C′
B′
注意:1.书写必须按角角边顺序排列;
2.相等的边必须是其中一相等
角的对边。
E
6cm
D
55°
45°
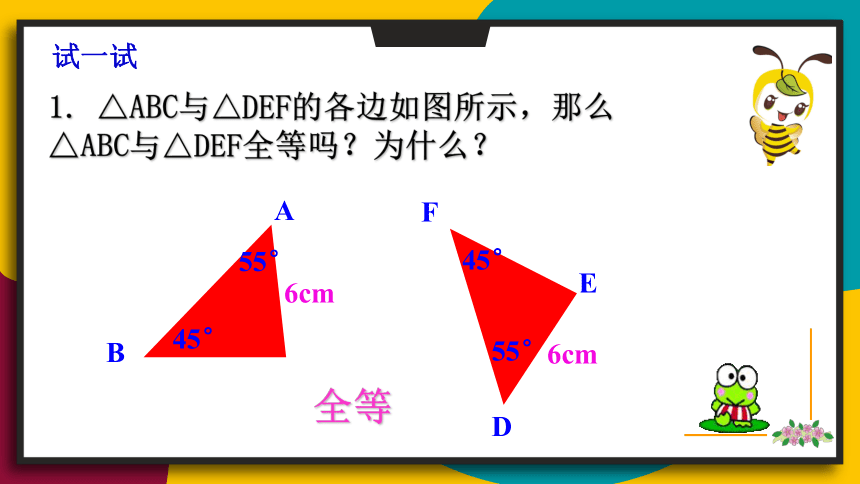
试一试
1. △ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?
A
B
F
45°
6cm
55°
全等
E
6cm
D
45°
55°
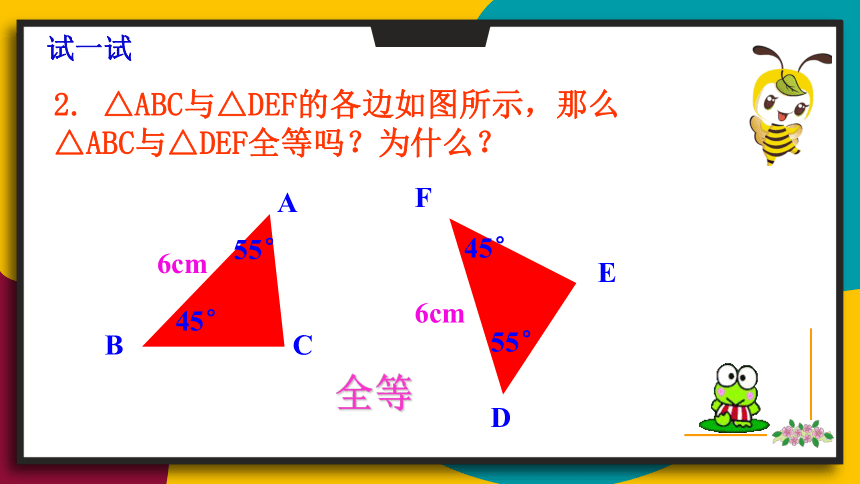
全等
2. △ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?
A
B
C
F
45°
6cm
55°
试一试
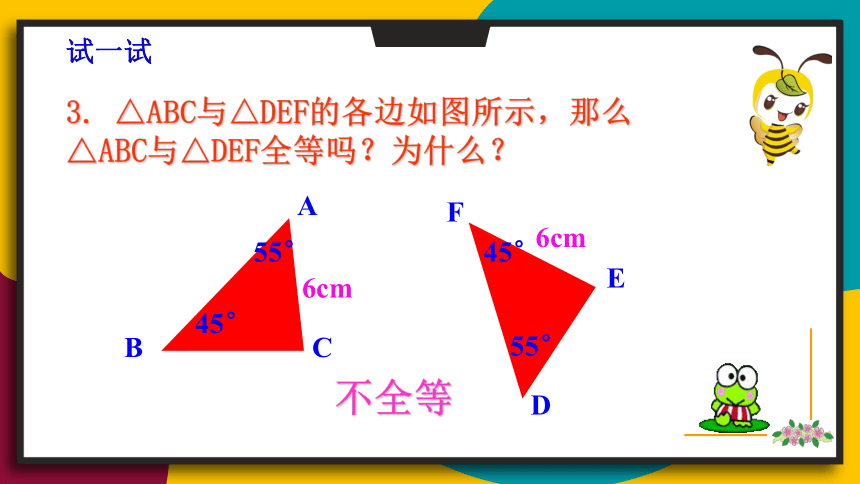
3. △ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?
A
B
C
F
E
45°
6cm
6cm
D
45°
55°
55°
试一试
不全等
1
2
A
B
D
C
∴AC=AB(全等三角形对应角相等)
如图,∠1=∠2,∠B=∠C.求证:△ABE≌△ACD
证明:在△ABD和△ACD中:
∠B=∠C(已知)
∠1=∠2(已知)
AD=AD(公共边)
∴ △ABE≌△ACD(AAS)
如果求证AC=AB呢
例1
做一做
如图,AB⊥BC,AD⊥DC, ∠1=∠2。求证:AB=AD
证明:∵ AB⊥BC AD⊥DC
∴ ∠B=∠D=90。
在△ABC和△ADC中:
∠B=∠D(已知)
∠1=∠2(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)
∴AB=AD(全等三角形对应角相等)
如图,已知AB=AC,∠ADB= ∠AEC。
求证:△ABD≌△ACE
证明:∵ AB=AC,
∴ ∠B= ∠C(等边对等角)
AB=AC (已知)
∠ADB=∠AEC (已知)
∠B=∠C (已证)
在△ABE与△ACD中:
∴ △ABD≌△ACE(AAS)
A
B
C
D
E
例2
练习:如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?
A
E
D
C
B
(全等三角形对应边相等)
∴ BE=CD
∴ △ABE ≌△ACD
AE=AD (已知)
∠B=∠C (已知)
∠A= ∠A(公共角)
在△ABE与△ACD中:
理由如下:
解:BE = CD
(AAS)
∠A=∠D,
AB=DE,
_________;
(AAS)
∠A=∠D,
AB=DE,
_________;
(SAS)
练习:79页习题第3的1小题
思考:按要求加条件,使各对三角形全等。
∠A=∠D,
AB=DE,
_________;
(ASA)
如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由。
试一试:74页练习第2题
1.若改为:AD、BE分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由。
2.若改为:AD、BE分别是两腰上的高,△ABD和△BAE全等吗?试说明理由。
ASA
SAS
AAS
1.学习了边角边、角边角、角角边;
2.注意角角边和角边角的区别;
3.会根据已知两角画三角形;
4.进一步学会应用公共角、公共边、对顶角、等边加等边、等角加等角隐含条件进行推理证明。
小 结
A
B
C
||
|||
|
A′
B′
C′
||
|||
|
两角分别相等且其中一组等角的对边相等的两个三角形全等。(可简写成“角角边”或“AAS”)。
作 业
P96复习题 第3、6题
谢谢欣赏
THANK YOU FOR LISTENING
如图,在△ABC中,D是边BC的中点,过点C 画直线CE,
使CE//AB, 交AD的延长线于点 E。求证:AD=ED
A
B
C
D
E
练习1
证明:∵ CE//AB(已知)
∴ ∠ ABD = ∠ECD ∠BAD= ∠ CED
(两直线平行,内错角相等)
在△ ABD与△ ECD中:
∴ △ ABD≌△ ECD (AAS)
∴ AD= ED (全等三角形的对应边相等)
∠ ABD = ∠ECD
∠BAD= ∠ CED(已证)
BD = CD(已知)
求证:全等三角形对应边的高相等。
已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高。求证:AD= A′D′
A
B
C
D
A ′
B ′
C ′
D ′
文字命题证明,需要画图,写出已知和求证
分析:从图中可以看出,AD、A'D'分别属于△ABD与△A'B'D',
要证AD = A'D',只需证明这两个三角形全等即可。
练习2
证明: ∵ △ABC≌△A′B′C′ (已知)
∴ AB=A′B′(全等三角形的对应边相等)
∵∠ B= ∠B′ (全等三角形的对应角相等)
在△ABD和△A′B′D′中,
∴ △ABD≌△A′B′D′(AAS)
∴AD = A′D′ (全等三角形的对应边相等)
∠ADB=∠A′D′B′ = 90 °(已知)
∠B=∠B′(已证)
AB=A′B′(已证)
于此类似,你能说明全等三角形对应边上的中线、对应角的平分线又有什么关系呢?
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
华师大版 八年级 上册
03
全等三角形判定——角角边(AAS)
复习提问:
全等三角形的判定方法:
1、图形变换(翻折、平移、旋转)
3、判定1边角边(SAS)
2、定义(六个元素)
4、判定2角边角(ASA)
复习提问:
几何语言:
E
F
A
B
C
D
AC=DF
成长的足迹
已知如图:AB⊥BC,AD⊥DC,∠1=∠2,AB=AD, 求证:BC=DC
A
C
D
B
1
2
证明: ∵ AB⊥BC AD⊥DC
∴ ∠ B=∠D=90 °
在△ABC和△ADC中:
∠1=∠2 (已知)
AB=AD (已知)
∠ B=∠D(已证)
∴ △ABC≌△ADC(ASA)
∴BC=DC
证明: 在△ABC和△ADC中:
AB=AD (已知)
∠1=∠2 (已知)
AC=AC (公共边)
∴ △ABC≌△ADC(SAS)
∴BC=DC
角边角
边角边
思考:如图:如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
已知:∠A=∠A′,∠B=∠B′,AC=A′C′
求证: △ABC≌△A′B′C′
证明:∵∠A=∠A′,∠B=∠B′
且∠A+∠B+∠C=180°
∠A′+∠B′+∠C′=180°
∴ ∠C=∠C′
在△ABC和△A′B′C′中
∠A=∠A′
AC=A′C′
∠C=∠C′
∴△ABC≌△A′B′C′(ASA)
归纳:如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等。
在△ABC和△ A'B'C'中
简记为 AAS 或角角边
∴△ABC≌△ A'B'C' (AAS)
∠A= ∠A'
BC= B'C'
∠B= ∠B'
A
C
B
A′
C′
B′
注意:1.书写必须按角角边顺序排列;
2.相等的边必须是其中一相等
角的对边。
E
6cm
D
55°
45°
试一试
1. △ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?
A
B
F
45°
6cm
55°
全等
E
6cm
D
45°
55°
全等
2. △ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?
A
B
C
F
45°
6cm
55°
试一试
3. △ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?
A
B
C
F
E
45°
6cm
6cm
D
45°
55°
55°
试一试
不全等
1
2
A
B
D
C
∴AC=AB(全等三角形对应角相等)
如图,∠1=∠2,∠B=∠C.求证:△ABE≌△ACD
证明:在△ABD和△ACD中:
∠B=∠C(已知)
∠1=∠2(已知)
AD=AD(公共边)
∴ △ABE≌△ACD(AAS)
如果求证AC=AB呢
例1
做一做
如图,AB⊥BC,AD⊥DC, ∠1=∠2。求证:AB=AD
证明:∵ AB⊥BC AD⊥DC
∴ ∠B=∠D=90。
在△ABC和△ADC中:
∠B=∠D(已知)
∠1=∠2(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)
∴AB=AD(全等三角形对应角相等)
如图,已知AB=AC,∠ADB= ∠AEC。
求证:△ABD≌△ACE
证明:∵ AB=AC,
∴ ∠B= ∠C(等边对等角)
AB=AC (已知)
∠ADB=∠AEC (已知)
∠B=∠C (已证)
在△ABE与△ACD中:
∴ △ABD≌△ACE(AAS)
A
B
C
D
E
例2
练习:如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?
A
E
D
C
B
(全等三角形对应边相等)
∴ BE=CD
∴ △ABE ≌△ACD
AE=AD (已知)
∠B=∠C (已知)
∠A= ∠A(公共角)
在△ABE与△ACD中:
理由如下:
解:BE = CD
(AAS)
∠A=∠D,
AB=DE,
_________;
(AAS)
∠A=∠D,
AB=DE,
_________;
(SAS)
练习:79页习题第3的1小题
思考:按要求加条件,使各对三角形全等。
∠A=∠D,
AB=DE,
_________;
(ASA)
如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由。
试一试:74页练习第2题
1.若改为:AD、BE分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由。
2.若改为:AD、BE分别是两腰上的高,△ABD和△BAE全等吗?试说明理由。
ASA
SAS
AAS
1.学习了边角边、角边角、角角边;
2.注意角角边和角边角的区别;
3.会根据已知两角画三角形;
4.进一步学会应用公共角、公共边、对顶角、等边加等边、等角加等角隐含条件进行推理证明。
小 结
A
B
C
||
|||
|
A′
B′
C′
||
|||
|
两角分别相等且其中一组等角的对边相等的两个三角形全等。(可简写成“角角边”或“AAS”)。
作 业
P96复习题 第3、6题
谢谢欣赏
THANK YOU FOR LISTENING
如图,在△ABC中,D是边BC的中点,过点C 画直线CE,
使CE//AB, 交AD的延长线于点 E。求证:AD=ED
A
B
C
D
E
练习1
证明:∵ CE//AB(已知)
∴ ∠ ABD = ∠ECD ∠BAD= ∠ CED
(两直线平行,内错角相等)
在△ ABD与△ ECD中:
∴ △ ABD≌△ ECD (AAS)
∴ AD= ED (全等三角形的对应边相等)
∠ ABD = ∠ECD
∠BAD= ∠ CED(已证)
BD = CD(已知)
求证:全等三角形对应边的高相等。
已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高。求证:AD= A′D′
A
B
C
D
A ′
B ′
C ′
D ′
文字命题证明,需要画图,写出已知和求证
分析:从图中可以看出,AD、A'D'分别属于△ABD与△A'B'D',
要证AD = A'D',只需证明这两个三角形全等即可。
练习2
证明: ∵ △ABC≌△A′B′C′ (已知)
∴ AB=A′B′(全等三角形的对应边相等)
∵∠ B= ∠B′ (全等三角形的对应角相等)
在△ABD和△A′B′D′中,
∴ △ABD≌△A′B′D′(AAS)
∴AD = A′D′ (全等三角形的对应边相等)
∠ADB=∠A′D′B′ = 90 °(已知)
∠B=∠B′(已证)
AB=A′B′(已证)
于此类似,你能说明全等三角形对应边上的中线、对应角的平分线又有什么关系呢?
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
