13.2.3.4三角形全等判定边边边(SSS)
文档属性
| 名称 | 13.2.3.4三角形全等判定边边边(SSS) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
华师大版 八年级 上册
04
全等三角形判定——边边边(SSS)
复习提问:
全等三角形的判定方法:
1、图形变换(翻折、平移、旋转)
3、判定1边角边(SAS)
2、定义(六个元素)
4、判定2角边角(ASA)
5、判定3角角边(AAS)
*
*
A
B
C
D
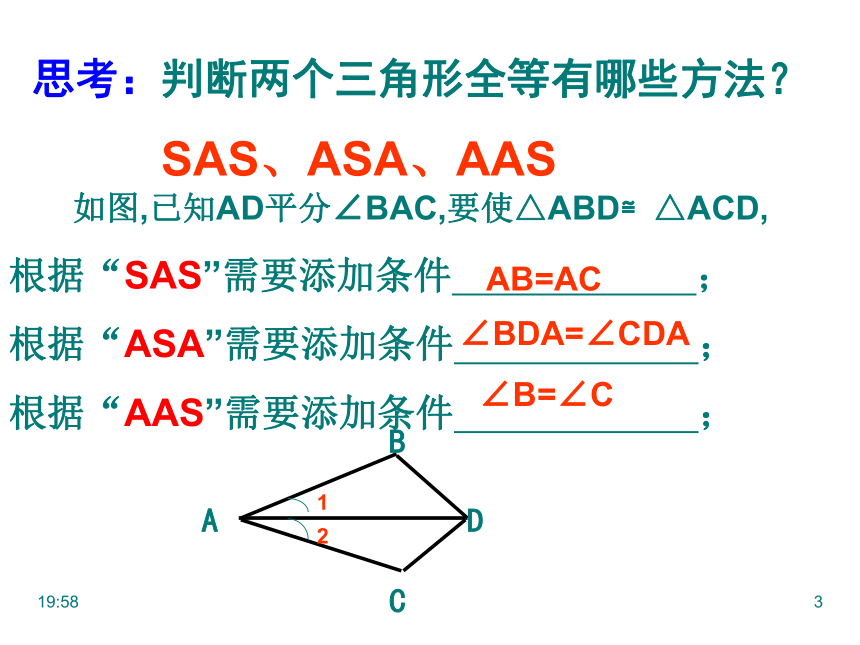
思考:判断两个三角形全等有哪些方法?
AB=AC
∠BDA=∠CDA
∠B=∠C
SAS、ASA、AAS
1
2
如图,已知AD平分∠BAC,要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
*
*
A
B
C
A′
B′
C′
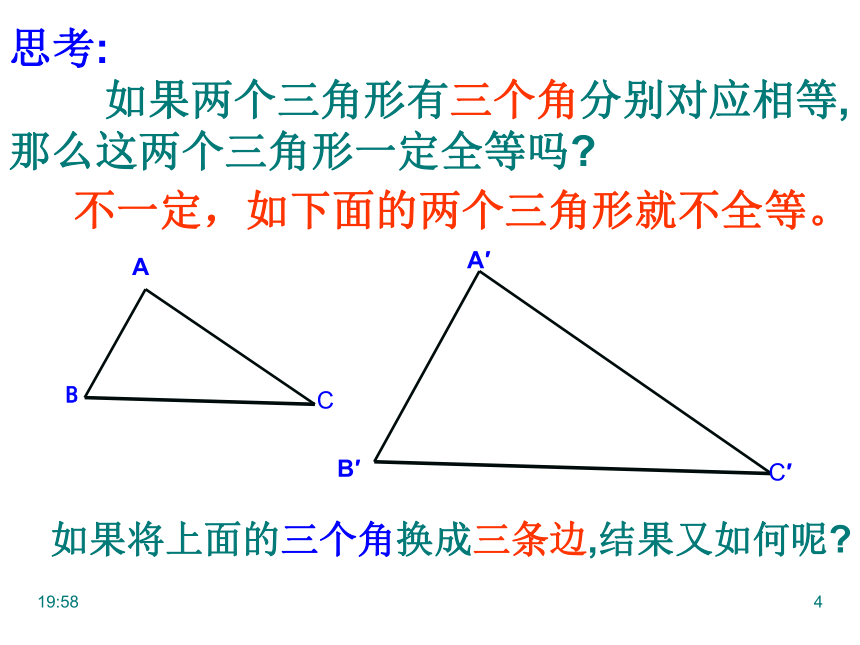
不一定,如下面的两个三角形就不全等。
思考:
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗
如果将上面的三个角换成三条边,结果又如何呢
*
*
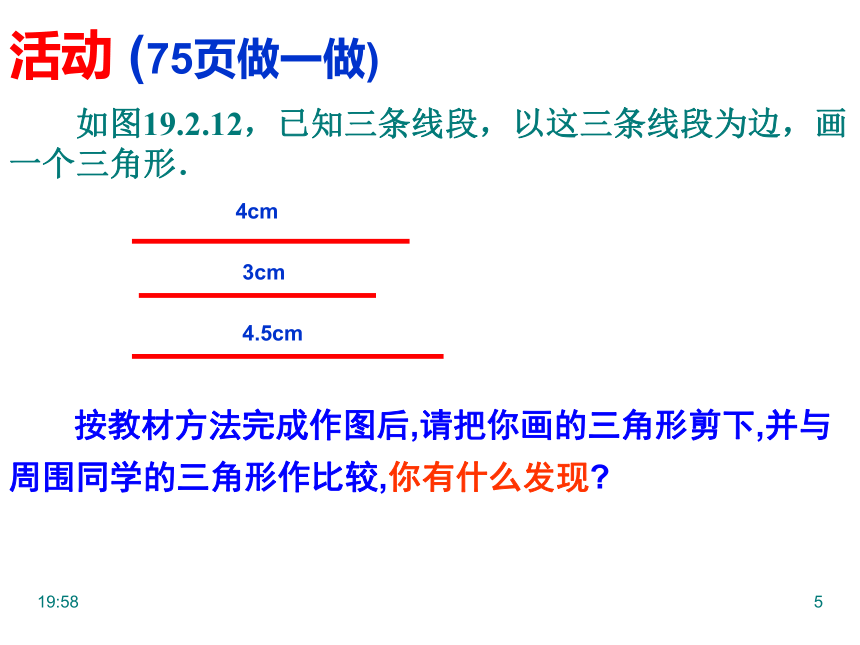
如图19.2.12,已知三条线段,以这三条线段为边,画一个三角形.
活动 (75页做一做)
4cm
3cm
4.5cm
按教材方法完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现
*
*
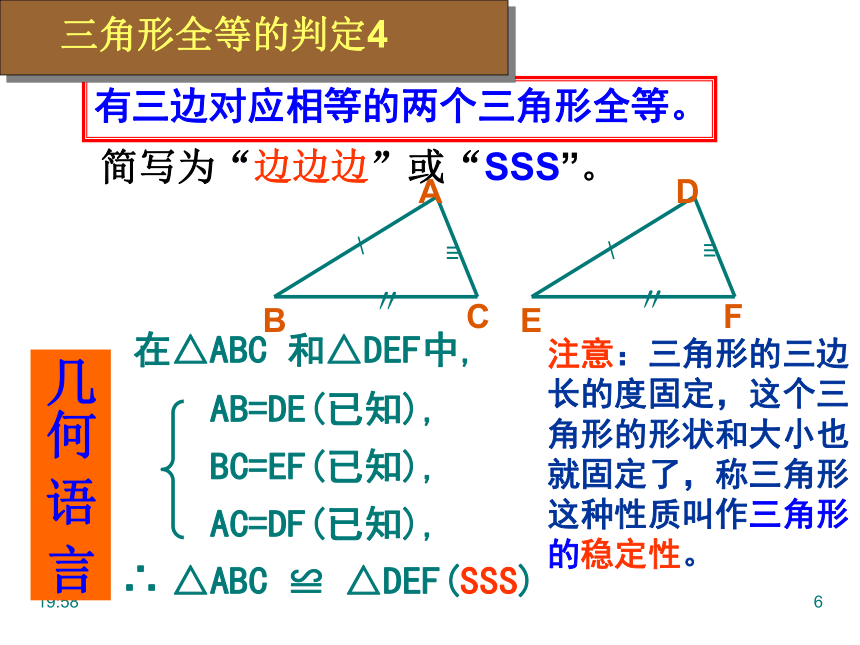
有三边对应相等的两个三角形全等。
A
B
C
D
E
F
〃
〃
\
\
≡
≡
在△ABC 和△DEF中,
AB=DE(已知),
BC=EF(已知),
AC=DF(已知),
△ABC ≌ △DEF(SSS)
∴
简写为“边边边”或“SSS”。
几何 语 言
注意:三角形的三边长的度固定,这个三角形的形状和大小也就固定了,称三角形这种性质叫作三角形的稳定性。
三角形全等的判定4
*
*
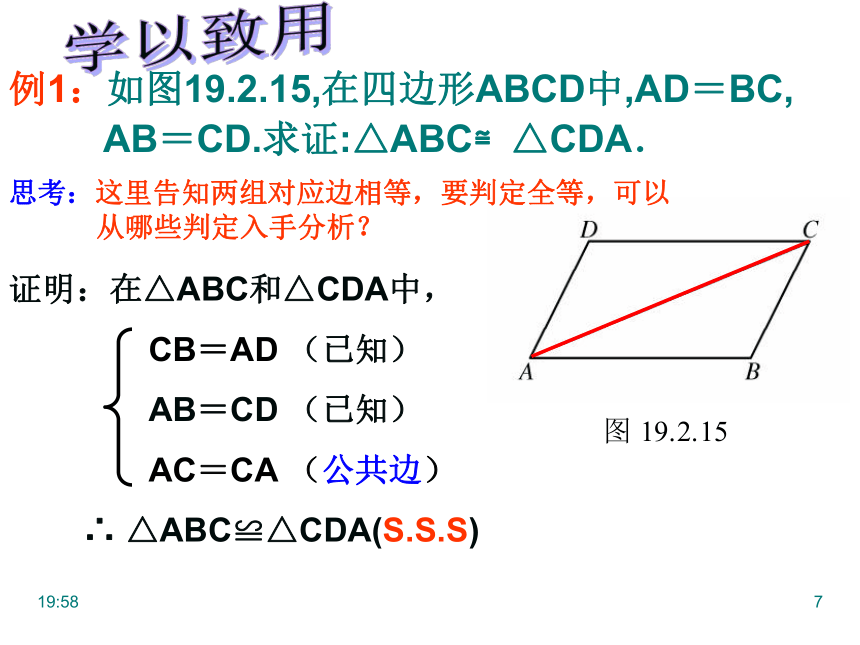
例1:如图19.2.15,在四边形ABCD中,AD=BC,
AB=CD.求证:△ABC≌△CDA.
证明:在△ABC和△CDA中,
CB=AD (已知)
AB=CD (已知)
AC=CA (公共边)
∴ △ABC≌△CDA(S.S.S)
思考:这里告知两组对应边相等,要判定全等,可以
从哪些判定入手分析?
*
*
如图,在四边形ABCD中,AD=BC,AB=CD.
求证:AB∥CD
A
B
C
D
证明:连结AC
在△ABC和△ ADC中
AB=CD(已知)
BC=DA(已知)
AC=CA(公共边)
∴△ABC≌ △CDA(SSS)
∴∠BAC=∠DCA( )
∴AB∥CD ( )
归纳:
1.经常把四边形问题转化为三角形问题,再通过三角形全等解决问题。
2.图中添加的辅助线实为两个三角形的公共边,这是以后经常要应用的方法。
*
*
做一做:
A
B
C
D
已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D
思考:连接BD能不能证明?
*
*
例2.已知:如图,点B、E、C、F在同一条直线上, AB=DE , AC = DF,BE = CF.求证: ∠A = ∠D
A
B
D
E
C
F
提示:
因为BE=CF
所以BE+CE=CF+CE
即BC=EF
由SSS得△ABC≌△DEF
证明:∵BE+CE=CF+CE
∴BC=EF
在△ABC和△ ADC中
AB=DE(已知)
BC=EF(已证)
AC=DF(已知)
∴△ ABC≌ △DEF( )
∴∠A=∠D( )
注意:在以后的全等证明中,经常会运用到“等量加等量得等量”这一性质去找边、角相等.
*
*
对应相等的元素 两边一角 两角一边
三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S)
不一定
一定
(A.S.A)
一定
(A.A.S)
不一定
一定
(S.S.S)
注意:判定三角形全等至少有一组边相等。
*
*
1. 全等(SAS)
全等(SSS)
不能判定全等。
全等(SSS等)
做一做:课本77练习1、2
2.解:①全等(用SSS或SAS或ASA或AAS都能证得)
②因为菱形和矩形都是平行四边形,所以有相同的结论;而梯形不是平行四边形,所以不有相同的结论。
*
*
1、“边边边”定理及其应用;
2、三角形的稳定性;
3、至此判定两个三角形全等已有四种方法:
“SAS”、“ASA’’、“AAS”、“SSS”.
*
*
作 业
P79习题19.2 第1题
P96复习题 第5、7题
华师大版 八年级 上册
04
全等三角形判定——边边边(SSS)
复习提问:
全等三角形的判定方法:
1、图形变换(翻折、平移、旋转)
3、判定1边角边(SAS)
2、定义(六个元素)
4、判定2角边角(ASA)
5、判定3角角边(AAS)
*
*
A
B
C
D
思考:判断两个三角形全等有哪些方法?
AB=AC
∠BDA=∠CDA
∠B=∠C
SAS、ASA、AAS
1
2
如图,已知AD平分∠BAC,要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
*
*
A
B
C
A′
B′
C′
不一定,如下面的两个三角形就不全等。
思考:
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗
如果将上面的三个角换成三条边,结果又如何呢
*
*
如图19.2.12,已知三条线段,以这三条线段为边,画一个三角形.
活动 (75页做一做)
4cm
3cm
4.5cm
按教材方法完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现
*
*
有三边对应相等的两个三角形全等。
A
B
C
D
E
F
〃
〃
\
\
≡
≡
在△ABC 和△DEF中,
AB=DE(已知),
BC=EF(已知),
AC=DF(已知),
△ABC ≌ △DEF(SSS)
∴
简写为“边边边”或“SSS”。
几何 语 言
注意:三角形的三边长的度固定,这个三角形的形状和大小也就固定了,称三角形这种性质叫作三角形的稳定性。
三角形全等的判定4
*
*
例1:如图19.2.15,在四边形ABCD中,AD=BC,
AB=CD.求证:△ABC≌△CDA.
证明:在△ABC和△CDA中,
CB=AD (已知)
AB=CD (已知)
AC=CA (公共边)
∴ △ABC≌△CDA(S.S.S)
思考:这里告知两组对应边相等,要判定全等,可以
从哪些判定入手分析?
*
*
如图,在四边形ABCD中,AD=BC,AB=CD.
求证:AB∥CD
A
B
C
D
证明:连结AC
在△ABC和△ ADC中
AB=CD(已知)
BC=DA(已知)
AC=CA(公共边)
∴△ABC≌ △CDA(SSS)
∴∠BAC=∠DCA( )
∴AB∥CD ( )
归纳:
1.经常把四边形问题转化为三角形问题,再通过三角形全等解决问题。
2.图中添加的辅助线实为两个三角形的公共边,这是以后经常要应用的方法。
*
*
做一做:
A
B
C
D
已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D
思考:连接BD能不能证明?
*
*
例2.已知:如图,点B、E、C、F在同一条直线上, AB=DE , AC = DF,BE = CF.求证: ∠A = ∠D
A
B
D
E
C
F
提示:
因为BE=CF
所以BE+CE=CF+CE
即BC=EF
由SSS得△ABC≌△DEF
证明:∵BE+CE=CF+CE
∴BC=EF
在△ABC和△ ADC中
AB=DE(已知)
BC=EF(已证)
AC=DF(已知)
∴△ ABC≌ △DEF( )
∴∠A=∠D( )
注意:在以后的全等证明中,经常会运用到“等量加等量得等量”这一性质去找边、角相等.
*
*
对应相等的元素 两边一角 两角一边
三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S)
不一定
一定
(A.S.A)
一定
(A.A.S)
不一定
一定
(S.S.S)
注意:判定三角形全等至少有一组边相等。
*
*
1. 全等(SAS)
全等(SSS)
不能判定全等。
全等(SSS等)
做一做:课本77练习1、2
2.解:①全等(用SSS或SAS或ASA或AAS都能证得)
②因为菱形和矩形都是平行四边形,所以有相同的结论;而梯形不是平行四边形,所以不有相同的结论。
*
*
1、“边边边”定理及其应用;
2、三角形的稳定性;
3、至此判定两个三角形全等已有四种方法:
“SAS”、“ASA’’、“AAS”、“SSS”.
*
*
作 业
P79习题19.2 第1题
P96复习题 第5、7题
