13.2.3.5 斜边直角边(HL定理) 课件(共26张PPT)
文档属性
| 名称 | 13.2.3.5 斜边直角边(HL定理) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
课前准备
请拿出你的课本、彩色笔和练习本等用品,还有你的激情和坐姿。
第13章 全等三角形
13.2.6 斜边直角边(HL定理)
1
复习引入
全等三角形的判定方法:
1、图形变换(翻折、平移、旋转)
3、判定1边角边(SAS)
2、定义(六个元素)
4、判定2角边角(ASA)
5、判定3角角边(AAS)
全等三角形的对应边 ,对应角 。
相等
相等
全等三角形的性质:
6、判定4边边边(SSS)
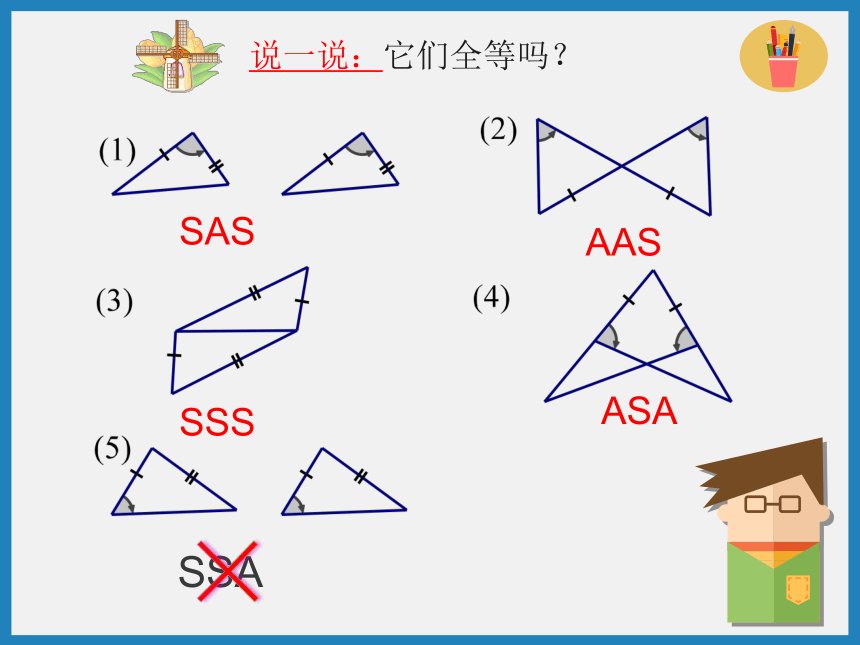
说一说:它们全等吗?
SAS
AAS
SSS
ASA
SSA
×
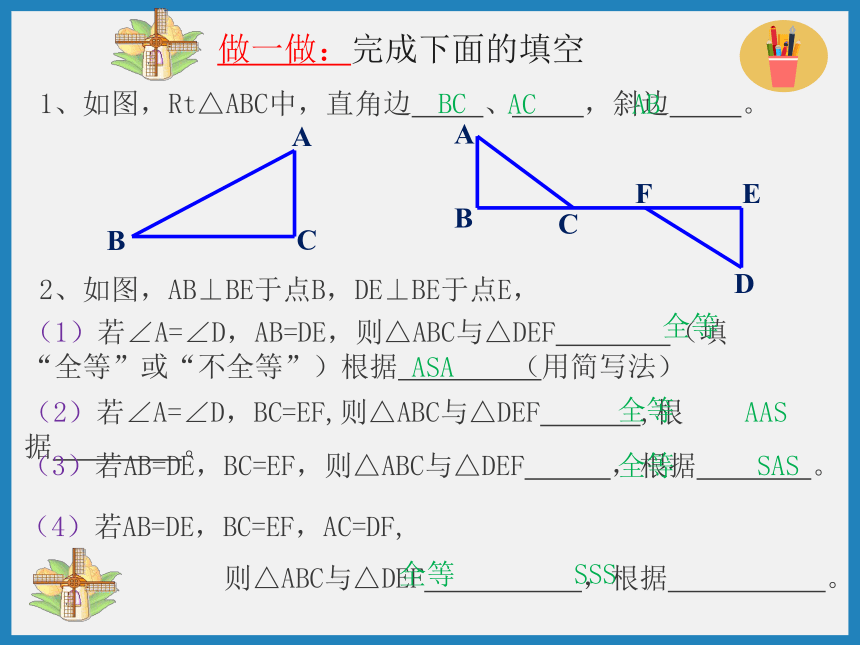
2、如图,AB⊥BE于点B,DE⊥BE于点E,
1、如图,Rt△ABC中,直角边 、 ,斜边 。
A
B
C
BC
AC
AB
(1)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)
A
B
C
D
E
F
全等
ASA
做一做:完成下面的填空
(2)若∠A=∠D,BC=EF,则△ABC与△DEF ,根据 。
AAS
全等
(3)若AB=DE,BC=EF,则△ABC与△DEF ,根据 。
全等
SAS
(4)若AB=DE,BC=EF,AC=DF,
则△ABC与△DEF ,根据 。
全等
SSS
2
探究新知
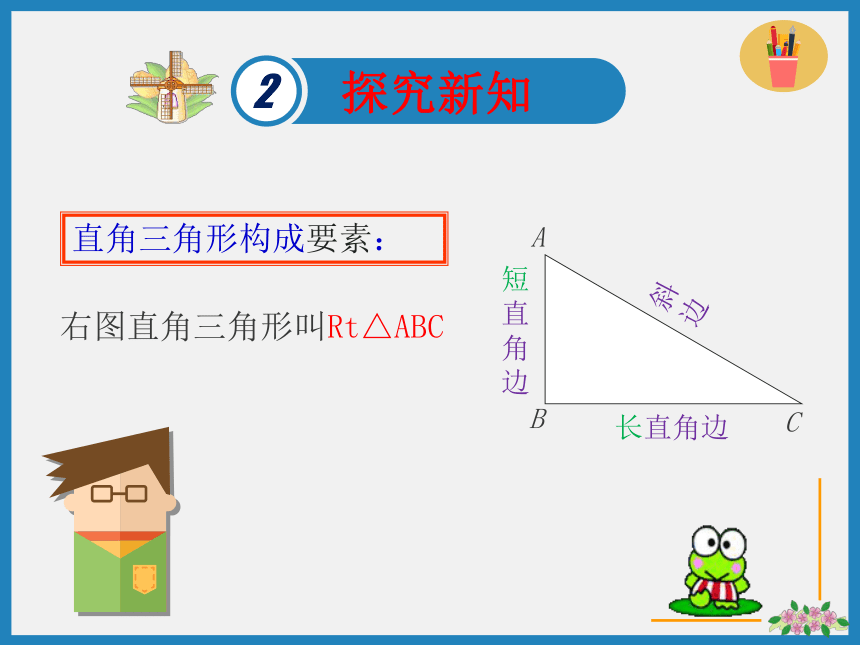
右图直角三角形叫Rt△ABC
长直角边
斜边
A
B
C
短直角边
直角三角形构成要素:
舞台背景形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
创设情境
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等。于是,他就肯定“两个直角三角形是全等的”。
(2)如果他只带一个卷尺,能完成这个任务吗
(1)你能帮他想个办法吗?
你相信的结论吗?
让我们来验证这个结论。
斜边和一条直角边对应相等→两个直角三角形全等
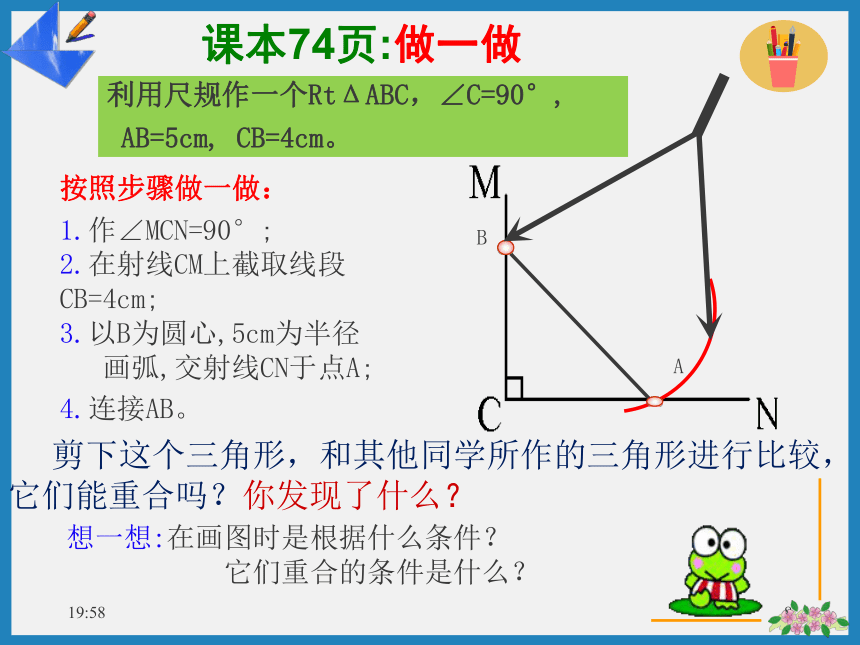
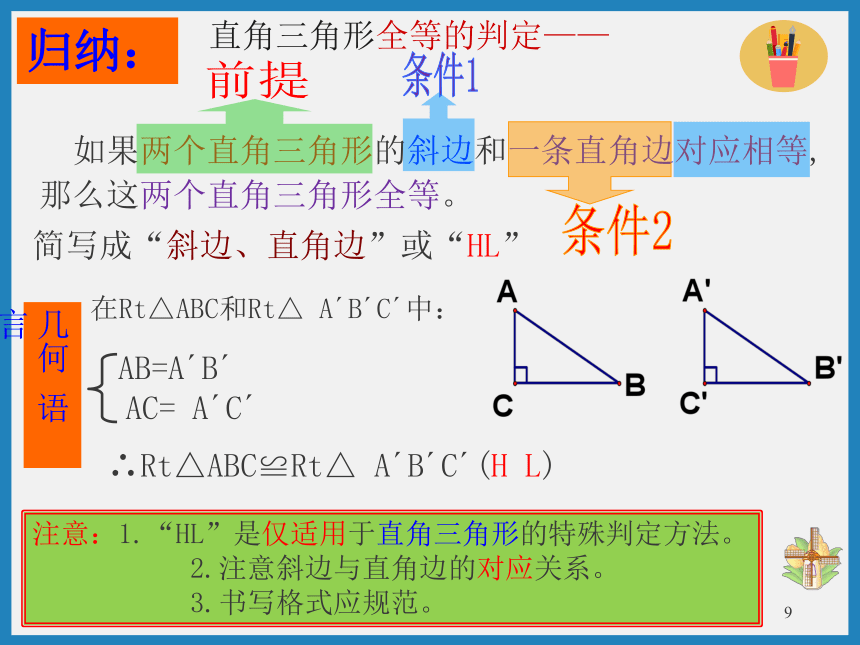
课本74页:做一做利用尺规作一个RtΔABC,∠C=90°,AB=5cm, CB=4cm。按照步骤做一做:1.作∠MCN=90°;2.在射线CM上截取线段CB=4cm;3.以B为圆心,5cm为半径 画弧,交射线CN于点A;4.连接AB。BA剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?你发现了什么?想一想:在画图时是根据什么条件?它们重合的条件是什么?如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。AB=A B AC= A C ∴Rt△ABC≌Rt△ A B C (H L)在Rt△ABC和Rt△ A B C 中:简写成“斜边、直角边”或“HL”直角三角形全等的判定——几何 语 言注意:1.“HL”是仅适用于直角三角形的特殊判定方法。2.注意斜边与直角边的对应关系。3.书写格式应规范。归纳:前提条件1条件22、判断:甲、乙、丙、丁四个直角三角形中全等的是( )
1
2
1
2
1
2
2
甲 乙 丙 丁
30°
乙丙丁
1、如图:AB⊥CD于O,OA=OB,
添加条件( ),
△AOC≌△BOD
A
D
B
C
O
3、如图,AC=AD,∠C=∠D=90°,
BD=3cm,则BC=( )cm
A
D
B
C
3
共有几种判断直角三角形全等的方法?
有两条边分别相等的两个直角三角形是否全等?
3
初显身手
思考:到现在为止,你能够用几种方法说明两个直角三角形全等?答:有五种——SAS、ASA、AAS、SSS、HL(1)AC=A′C′,∠A=∠A′( )(2)AC=A′C′,BC=B′C′( )(3)AB=A′B′,∠A=∠A′( )(4)∠A=∠A′,∠B=∠B′( )(5)AC=A′C′,AB=A′B′( )练习:Rt△ABC与Rt△A′B′C′中∠C=∠C′=90。,根据下列条件判断是否全等,并说明理由。ASASAS×AASHL如图,已知AC=BD,∠D=∠C=90°求证:Rt△ABC≌Rt△BAD证明:∵∠D=∠C=90°∴△ABC和△BAD是Rt△在Rt△ABC和Rt△BAD中:AB=ABAC=BD∴Rt△ABC≌Rt△BAD(?)∟∟ABCD∴BC=AD (全等三角形的对应边相等)思考:如果要证BC=AD,如何做 做一做:课本75页练习1。4例题讲解例1已知:如图,D是BC边的中点,DF⊥AC、DE⊥AB,垂足分别为E、F,
且DE=DF。求证: AB=AC
证明:∵ DE⊥AB,DF⊥AC
∴ △BDE 和 △CDF是Rt △
∵ D是BC边的中点
∴BD=CD
在Rt △BDE ≌ Rt △CDF
DE=DF (已知)
BD=CD(已证)
∴ Rt △BDE ≌ Rt △CDF(HL)
∴∠B=∠C(全等三角形对应角相等)
∴AB=AC(等角对等边)
教材练习1
做一做:课本75页练习2。
如图,在△ABC中,已知BD⊥AC,CE⊥AB,BD=CE。求证:△EBC≌ △DCBABC∟∟ED证明:∵CE ⊥AB,BD⊥AC∴ △EBC和△DCB都是直角三角形在Rt △EBC和Rt△DCB中:BD=CE(已知)BC=CB(公共边)∴Rt △EBC≌ Rt△DCB (HL)试一试如图,在△ABC与△A’B’C’中,CD、C’D’分别是高,并且AC=A’C’,CD=C’D’,∠ACB=∠A’C’B’。
求证:△ABC≌△A’B’C’
证明: ∵ CD、C’D’分别是高
∴△ADC和△A’D’C’是Rt △
在Rt△ADC和Rt△A’D’C’中:
AC=A’C’ (已知)
CD=C’D’ (已知)
∴Rt△ABC≌ Rt△A’D’C’ (HL)
∴ ∠A=∠A’
在△ ABC和△ A’B’C’中:
∠A=∠A’ (已证)
AC=A’C’ (已知)
∠ACB=∠A’ B’C’ (已知)
∴ △ABC≌ △ A’B’C’(ASA)
例2
变式训练
如图,已知AC=BD,∠ACB=∠BDA=90°
求证:AD=BC
A
D
B
C
E
方法一
变式训练
如图,已知AC=BD,∠ACB=∠BDA=90°
求证:AD=BC
A
D
B
C
E
方法二
M
基 础 过 关1.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )A.HLB.SASC.ASAD.AASA 2.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“H.L.”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( )A.AE=DFB.∠A=∠DC.∠B=∠CD.AB=DCD 基 础 过 关3.如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )A.AO=COB.DO=EOC.AD=CED.∠A=∠CD 基 础 过 关4.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )A.40°B.50°C.60°D.75°B 基 础 过 关任意三角形 全等的判定方法:
(1)边边边(SSS)
(2)边角边(SAS)
(3)角边角(ASA)
(4)角角边(AAS)
直角三角形 全等专属
(5)斜边直角边(HL)
适用于直角三角形
5
课堂小结
灵活运用各种方法证明直角三角形全等
6作业P79习题19.2第6题P96复习题 第8、9题不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
学习要一步一个脚印
同学们:你们是最棒的!
奥利给!
谢谢欣赏
THANK YOU FOR LISTENING
课前准备
请拿出你的课本、彩色笔和练习本等用品,还有你的激情和坐姿。
第13章 全等三角形
13.2.6 斜边直角边(HL定理)
1
复习引入
全等三角形的判定方法:
1、图形变换(翻折、平移、旋转)
3、判定1边角边(SAS)
2、定义(六个元素)
4、判定2角边角(ASA)
5、判定3角角边(AAS)
全等三角形的对应边 ,对应角 。
相等
相等
全等三角形的性质:
6、判定4边边边(SSS)
说一说:它们全等吗?
SAS
AAS
SSS
ASA
SSA
×
2、如图,AB⊥BE于点B,DE⊥BE于点E,
1、如图,Rt△ABC中,直角边 、 ,斜边 。
A
B
C
BC
AC
AB
(1)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)
A
B
C
D
E
F
全等
ASA
做一做:完成下面的填空
(2)若∠A=∠D,BC=EF,则△ABC与△DEF ,根据 。
AAS
全等
(3)若AB=DE,BC=EF,则△ABC与△DEF ,根据 。
全等
SAS
(4)若AB=DE,BC=EF,AC=DF,
则△ABC与△DEF ,根据 。
全等
SSS
2
探究新知
右图直角三角形叫Rt△ABC
长直角边
斜边
A
B
C
短直角边
直角三角形构成要素:
舞台背景形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
创设情境
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等。于是,他就肯定“两个直角三角形是全等的”。
(2)如果他只带一个卷尺,能完成这个任务吗
(1)你能帮他想个办法吗?
你相信的结论吗?
让我们来验证这个结论。
斜边和一条直角边对应相等→两个直角三角形全等
课本74页:做一做利用尺规作一个RtΔABC,∠C=90°,AB=5cm, CB=4cm。按照步骤做一做:1.作∠MCN=90°;2.在射线CM上截取线段CB=4cm;3.以B为圆心,5cm为半径 画弧,交射线CN于点A;4.连接AB。BA剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?你发现了什么?想一想:在画图时是根据什么条件?它们重合的条件是什么?如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。AB=A B AC= A C ∴Rt△ABC≌Rt△ A B C (H L)在Rt△ABC和Rt△ A B C 中:简写成“斜边、直角边”或“HL”直角三角形全等的判定——几何 语 言注意:1.“HL”是仅适用于直角三角形的特殊判定方法。2.注意斜边与直角边的对应关系。3.书写格式应规范。归纳:前提条件1条件22、判断:甲、乙、丙、丁四个直角三角形中全等的是( )
1
2
1
2
1
2
2
甲 乙 丙 丁
30°
乙丙丁
1、如图:AB⊥CD于O,OA=OB,
添加条件( ),
△AOC≌△BOD
A
D
B
C
O
3、如图,AC=AD,∠C=∠D=90°,
BD=3cm,则BC=( )cm
A
D
B
C
3
共有几种判断直角三角形全等的方法?
有两条边分别相等的两个直角三角形是否全等?
3
初显身手
思考:到现在为止,你能够用几种方法说明两个直角三角形全等?答:有五种——SAS、ASA、AAS、SSS、HL(1)AC=A′C′,∠A=∠A′( )(2)AC=A′C′,BC=B′C′( )(3)AB=A′B′,∠A=∠A′( )(4)∠A=∠A′,∠B=∠B′( )(5)AC=A′C′,AB=A′B′( )练习:Rt△ABC与Rt△A′B′C′中∠C=∠C′=90。,根据下列条件判断是否全等,并说明理由。ASASAS×AASHL如图,已知AC=BD,∠D=∠C=90°求证:Rt△ABC≌Rt△BAD证明:∵∠D=∠C=90°∴△ABC和△BAD是Rt△在Rt△ABC和Rt△BAD中:AB=ABAC=BD∴Rt△ABC≌Rt△BAD(?)∟∟ABCD∴BC=AD (全等三角形的对应边相等)思考:如果要证BC=AD,如何做 做一做:课本75页练习1。4例题讲解例1已知:如图,D是BC边的中点,DF⊥AC、DE⊥AB,垂足分别为E、F,
且DE=DF。求证: AB=AC
证明:∵ DE⊥AB,DF⊥AC
∴ △BDE 和 △CDF是Rt △
∵ D是BC边的中点
∴BD=CD
在Rt △BDE ≌ Rt △CDF
DE=DF (已知)
BD=CD(已证)
∴ Rt △BDE ≌ Rt △CDF(HL)
∴∠B=∠C(全等三角形对应角相等)
∴AB=AC(等角对等边)
教材练习1
做一做:课本75页练习2。
如图,在△ABC中,已知BD⊥AC,CE⊥AB,BD=CE。求证:△EBC≌ △DCBABC∟∟ED证明:∵CE ⊥AB,BD⊥AC∴ △EBC和△DCB都是直角三角形在Rt △EBC和Rt△DCB中:BD=CE(已知)BC=CB(公共边)∴Rt △EBC≌ Rt△DCB (HL)试一试如图,在△ABC与△A’B’C’中,CD、C’D’分别是高,并且AC=A’C’,CD=C’D’,∠ACB=∠A’C’B’。
求证:△ABC≌△A’B’C’
证明: ∵ CD、C’D’分别是高
∴△ADC和△A’D’C’是Rt △
在Rt△ADC和Rt△A’D’C’中:
AC=A’C’ (已知)
CD=C’D’ (已知)
∴Rt△ABC≌ Rt△A’D’C’ (HL)
∴ ∠A=∠A’
在△ ABC和△ A’B’C’中:
∠A=∠A’ (已证)
AC=A’C’ (已知)
∠ACB=∠A’ B’C’ (已知)
∴ △ABC≌ △ A’B’C’(ASA)
例2
变式训练
如图,已知AC=BD,∠ACB=∠BDA=90°
求证:AD=BC
A
D
B
C
E
方法一
变式训练
如图,已知AC=BD,∠ACB=∠BDA=90°
求证:AD=BC
A
D
B
C
E
方法二
M
基 础 过 关1.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )A.HLB.SASC.ASAD.AASA 2.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“H.L.”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( )A.AE=DFB.∠A=∠DC.∠B=∠CD.AB=DCD 基 础 过 关3.如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )A.AO=COB.DO=EOC.AD=CED.∠A=∠CD 基 础 过 关4.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )A.40°B.50°C.60°D.75°B 基 础 过 关任意三角形 全等的判定方法:
(1)边边边(SSS)
(2)边角边(SAS)
(3)角边角(ASA)
(4)角角边(AAS)
直角三角形 全等专属
(5)斜边直角边(HL)
适用于直角三角形
5
课堂小结
灵活运用各种方法证明直角三角形全等
6作业P79习题19.2第6题P96复习题 第8、9题不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
学习要一步一个脚印
同学们:你们是最棒的!
奥利给!
谢谢欣赏
THANK YOU FOR LISTENING
