13.5.1 互逆命题与互逆定理 课件(共23张PPT)
文档属性
| 名称 | 13.5.1 互逆命题与互逆定理 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
13.5.1互逆命题与互逆定理第13章逆命题与逆定理
1.什么叫命题?
可以判断正确或错误的句子叫做命题。
由条件和结论两部分组成。
2.命题由几部分组成,一般可以写成什么样的形式
可以写成“如果……,那么……”的形式。
3.什么是定理?
基本事实或其他真命题证明是正确的,并可以作为证明其他命题真假依据的真命题。
知识回顾
(1)你喜欢数学吗?
(2)两条直线平行,内错角相等。
(3)任何一个三角形一定有直角。
(4)作线段AB=CD。
注意:疑问句、祈使句、感叹句和几何作法不是命题!
不是命题
是命题
是命题
不是命题
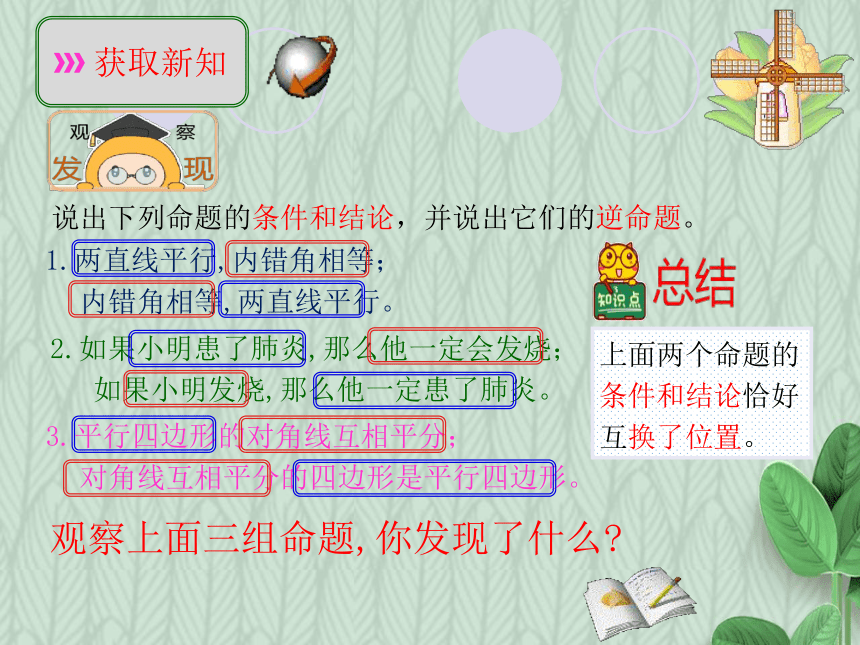
说出下列命题的条件和结论,并说出它们的逆命题。
1.两直线平行,内错角相等;
内错角相等,两直线平行。
2.如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎。
3.平行四边形的对角线互相平分;
对角线互相平分的四边形是平行四边形。
观察上面三组命题,你发现了什么
上面两个命题的条件和结论恰好互换了位置。
获取新知
一般来说,在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做互逆命题。
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题。
求一个命题的逆命题的方法:
命题“两直线平行,内错角相等”的
条件为: ;
结论为: 。
因此它的逆命题为_______________________。
两直线平行
内错角相等
内错角相等,两直线平行
每一个命题都有逆命题,只要将原命题的条件改成结论,并将结论改成条件,便可得到原命题的逆命题。
例如
真命题“对顶角相等”的逆命题为“相等的角是对顶角”,
此命题就是假命题。
但是原命题正确,它的逆命题未必正确。
2.等边三角形的每个角都等于60°题设:一个三角形是等边三角形。结论:它的每个角都等于60°。逆命题:如果一个三角形的每个角都等于60°,那么这个三角形是等边三角形。例1:指出下列命题题设和结论,并说出它们的逆命题。1.如果一个三角形是直角三角形,那么它的两个锐角互余。题设:一个三角形是直角三角形。结论:它的两个锐角互余。逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形。做一做:课本93页练习第1题3、4、5小题。例题讲解(1)如果一个三角形是直角三角形,那么它的两个锐角互余。逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形。判断(1)、(2)原命题和逆命题是否正确,试着给出你的结论(2)全等三角形的对应角相等。逆命题:如果两个三角形的对应角相等,那么这两个三角形全等。√×√√
互逆定理
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理。
例如“两直线平行,内错角相等”与 “内错角相等,两直线平行”为互逆定理
1.逆命题、互逆命题不一定是真命题,
但逆定理、互逆定理,一定是真命题。
2.不是所有的定理都有逆定理。
你能举例说明吗?
一个假命题的逆命题可以是真命题,甚至可以是定理。
例如“相等的角是对顶角”是假命题,但它的逆命题“对顶角相等”是真命题,且是定理。
命题“两直线平行,同位角相等”和它的逆命题“同位角相等,两直线平行”都是定理,因此它们就是互逆定理。
定理对顶角相等就没有逆定理
1.每一个命题都有逆命题,只要将原命题的题设和结论对换,便可得到原命题的逆命题;2.原命题正确,它的逆命题未必正确;原命题错误,它的逆命题未必错误;归纳:原命题:如果两个角相等,那么这两个角是直角。逆命题:如果两个角都是直角,那么这两个角相等。原命题:对顶角相等。逆命题:相等的角是对顶角。例如:课本93页练习第2题。例2 判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0。
例题讲解
解:(1)原命题是真命题。逆命题为:如果两条直线只有
一个交点,那么它们相交。逆命题是真命题。
(2)原命题是假命题。逆命题为:如果a2>b2,那么
a>b。逆命题是假命题。
(3)原命题是真命题。逆命题为:如果两个数的和为
零,那么它们互为相反数。逆命题是真命题。
(4)原命题是假命题。逆命题为:如果a>0,b<0,
那么ab<0。逆命题是真命题。
(1)两条直线平行,内错角相等。(2)等角对等边。说出下列命题的逆命题。这些命题的逆命题成立吗 逆命题:内错角相等,两条直线平行。逆命题:等边对等角。思考:两个例题原命题和逆命与前面有何不同 成立成立原命题和逆命题不但是真命题还是定理定理逆定理原命题逆命题证明证明命题与定理的关系:真真注意:1原命题、逆命题和互逆命不一定是真命题,但逆定理、互逆定理,一定是真命题。2不是所有的定理都有逆定理。说出下列定理的逆命题。与原命题成互逆定理吗 同位角相等,两条直线平行.题设结论题设结论互换同位角相等。两条直线平行,逆命题为:成立①掌握逆命题、逆定理的概念。②能写出一个命题的逆命题。③在证明假命题时会用举反例说明。课堂总结互逆命题与互逆定理
互逆命题
互逆定理
一个定理的逆命题也是定理,这两个定理叫做互逆定理。
第一个命题的条件是第二个命题的结论;
第一个命题的结论是第二个命题的条件。
概念
概念
课堂总结
P98习题13.5第1题P103习题复习题第1、2题课后作业1.下列说法中正确的是( )
A.每个命题都有逆命题
B.每个定理都有逆定理
C.真命题的逆命题都是真命题
D.假命题的逆命题都是真命题
A
基 础 过 关
2. 命题“若一个数是负数,则它的平方是正数”的逆命题是( )
A.若一个数是正数,则它的平方是负数
B.若一个数的平方是正数,则它是负数
C.若一个数不是负数,则它的平方不是正数
D.若一个数的平方不是正数,则它不是正数
B
基 础 过 关
3. 下列定理中,没有逆定理的是( )
A.两直线平行,同旁内角互补
B.全等三角形的对应角相等
C.直角三角形的两个锐角互余
D.两内角相等的三角形是等腰三角形
B
基 础 过 关
4. 下列命题:
①内错角相等,两直线平行;
②全等三角形的对应边相等;
③若a=b,则a2=b2;
④互补的角为邻补角;
⑤对顶角相等;
它们的逆命题是真命题的有 (只填序号)。
①
②
④
基 础 过 关
5.命题“同角的补角相等”的条件____________________,结论是___________;它的逆命_________________________。6.【安徽中考】命题“如果a+b=0,那么a、b互为相反数”的逆命题为_______________________________。7.写出定理“两直线平行,同位角相等”的逆定理是____________________。两个角是同一个角的补角 这两个角相等 补角相等的两个角是同一个角 如果a、b互为相反数,那么a+b=0同位角相等,两直线平行 基 础 过 关
谢谢欣赏
THANK YOU FOR LISTENING
13.5.1互逆命题与互逆定理第13章逆命题与逆定理
1.什么叫命题?
可以判断正确或错误的句子叫做命题。
由条件和结论两部分组成。
2.命题由几部分组成,一般可以写成什么样的形式
可以写成“如果……,那么……”的形式。
3.什么是定理?
基本事实或其他真命题证明是正确的,并可以作为证明其他命题真假依据的真命题。
知识回顾
(1)你喜欢数学吗?
(2)两条直线平行,内错角相等。
(3)任何一个三角形一定有直角。
(4)作线段AB=CD。
注意:疑问句、祈使句、感叹句和几何作法不是命题!
不是命题
是命题
是命题
不是命题
说出下列命题的条件和结论,并说出它们的逆命题。
1.两直线平行,内错角相等;
内错角相等,两直线平行。
2.如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎。
3.平行四边形的对角线互相平分;
对角线互相平分的四边形是平行四边形。
观察上面三组命题,你发现了什么
上面两个命题的条件和结论恰好互换了位置。
获取新知
一般来说,在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做互逆命题。
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题。
求一个命题的逆命题的方法:
命题“两直线平行,内错角相等”的
条件为: ;
结论为: 。
因此它的逆命题为_______________________。
两直线平行
内错角相等
内错角相等,两直线平行
每一个命题都有逆命题,只要将原命题的条件改成结论,并将结论改成条件,便可得到原命题的逆命题。
例如
真命题“对顶角相等”的逆命题为“相等的角是对顶角”,
此命题就是假命题。
但是原命题正确,它的逆命题未必正确。
2.等边三角形的每个角都等于60°题设:一个三角形是等边三角形。结论:它的每个角都等于60°。逆命题:如果一个三角形的每个角都等于60°,那么这个三角形是等边三角形。例1:指出下列命题题设和结论,并说出它们的逆命题。1.如果一个三角形是直角三角形,那么它的两个锐角互余。题设:一个三角形是直角三角形。结论:它的两个锐角互余。逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形。做一做:课本93页练习第1题3、4、5小题。例题讲解(1)如果一个三角形是直角三角形,那么它的两个锐角互余。逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形。判断(1)、(2)原命题和逆命题是否正确,试着给出你的结论(2)全等三角形的对应角相等。逆命题:如果两个三角形的对应角相等,那么这两个三角形全等。√×√√
互逆定理
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理。
例如“两直线平行,内错角相等”与 “内错角相等,两直线平行”为互逆定理
1.逆命题、互逆命题不一定是真命题,
但逆定理、互逆定理,一定是真命题。
2.不是所有的定理都有逆定理。
你能举例说明吗?
一个假命题的逆命题可以是真命题,甚至可以是定理。
例如“相等的角是对顶角”是假命题,但它的逆命题“对顶角相等”是真命题,且是定理。
命题“两直线平行,同位角相等”和它的逆命题“同位角相等,两直线平行”都是定理,因此它们就是互逆定理。
定理对顶角相等就没有逆定理
1.每一个命题都有逆命题,只要将原命题的题设和结论对换,便可得到原命题的逆命题;2.原命题正确,它的逆命题未必正确;原命题错误,它的逆命题未必错误;归纳:原命题:如果两个角相等,那么这两个角是直角。逆命题:如果两个角都是直角,那么这两个角相等。原命题:对顶角相等。逆命题:相等的角是对顶角。例如:课本93页练习第2题。例2 判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0。
例题讲解
解:(1)原命题是真命题。逆命题为:如果两条直线只有
一个交点,那么它们相交。逆命题是真命题。
(2)原命题是假命题。逆命题为:如果a2>b2,那么
a>b。逆命题是假命题。
(3)原命题是真命题。逆命题为:如果两个数的和为
零,那么它们互为相反数。逆命题是真命题。
(4)原命题是假命题。逆命题为:如果a>0,b<0,
那么ab<0。逆命题是真命题。
(1)两条直线平行,内错角相等。(2)等角对等边。说出下列命题的逆命题。这些命题的逆命题成立吗 逆命题:内错角相等,两条直线平行。逆命题:等边对等角。思考:两个例题原命题和逆命与前面有何不同 成立成立原命题和逆命题不但是真命题还是定理定理逆定理原命题逆命题证明证明命题与定理的关系:真真注意:1原命题、逆命题和互逆命不一定是真命题,但逆定理、互逆定理,一定是真命题。2不是所有的定理都有逆定理。说出下列定理的逆命题。与原命题成互逆定理吗 同位角相等,两条直线平行.题设结论题设结论互换同位角相等。两条直线平行,逆命题为:成立①掌握逆命题、逆定理的概念。②能写出一个命题的逆命题。③在证明假命题时会用举反例说明。课堂总结互逆命题与互逆定理
互逆命题
互逆定理
一个定理的逆命题也是定理,这两个定理叫做互逆定理。
第一个命题的条件是第二个命题的结论;
第一个命题的结论是第二个命题的条件。
概念
概念
课堂总结
P98习题13.5第1题P103习题复习题第1、2题课后作业1.下列说法中正确的是( )
A.每个命题都有逆命题
B.每个定理都有逆定理
C.真命题的逆命题都是真命题
D.假命题的逆命题都是真命题
A
基 础 过 关
2. 命题“若一个数是负数,则它的平方是正数”的逆命题是( )
A.若一个数是正数,则它的平方是负数
B.若一个数的平方是正数,则它是负数
C.若一个数不是负数,则它的平方不是正数
D.若一个数的平方不是正数,则它不是正数
B
基 础 过 关
3. 下列定理中,没有逆定理的是( )
A.两直线平行,同旁内角互补
B.全等三角形的对应角相等
C.直角三角形的两个锐角互余
D.两内角相等的三角形是等腰三角形
B
基 础 过 关
4. 下列命题:
①内错角相等,两直线平行;
②全等三角形的对应边相等;
③若a=b,则a2=b2;
④互补的角为邻补角;
⑤对顶角相等;
它们的逆命题是真命题的有 (只填序号)。
①
②
④
基 础 过 关
5.命题“同角的补角相等”的条件____________________,结论是___________;它的逆命_________________________。6.【安徽中考】命题“如果a+b=0,那么a、b互为相反数”的逆命题为_______________________________。7.写出定理“两直线平行,同位角相等”的逆定理是____________________。两个角是同一个角的补角 这两个角相等 补角相等的两个角是同一个角 如果a、b互为相反数,那么a+b=0同位角相等,两直线平行 基 础 过 关
谢谢欣赏
THANK YOU FOR LISTENING
