13.5.2 线段垂直平分线 课件(共22张PPT)
文档属性
| 名称 | 13.5.2 线段垂直平分线 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 06:06:00 | ||
图片预览




文档简介
(共22张PPT)
*
*
13.5.2 线段垂直平分线
第13章 逆命题与逆定理
创设情境
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
*
*
1、什么叫线段垂直平分线?
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2、线段垂直平分线有什么性质?
线段垂直平分线上的点与这条线段的两个端点的距离相等 。
你能画图证明吗?
知识回顾
*
*
A
B
P
M
N
C
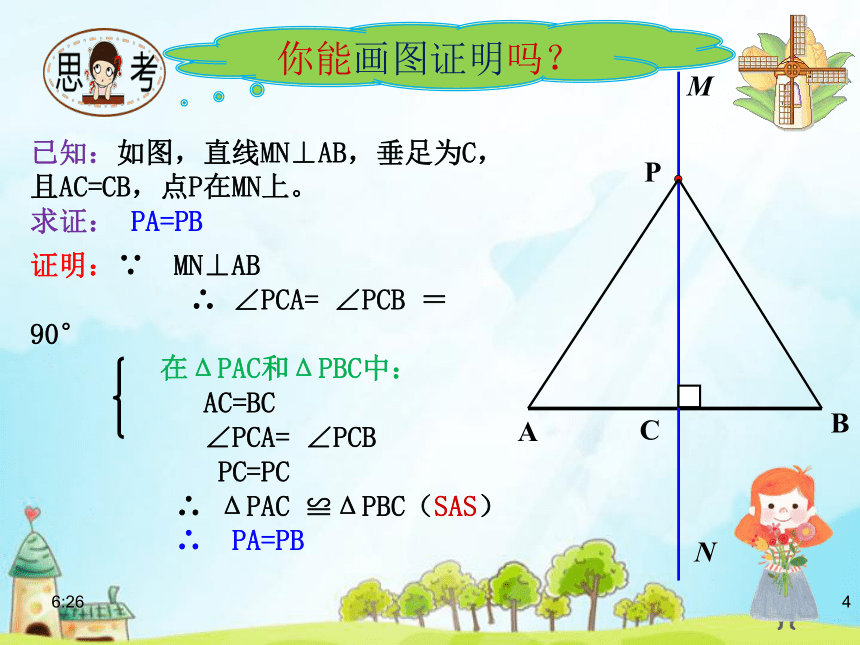
已知:如图,直线MN⊥AB,垂足为C,
且AC=CB,点P在MN上。
求证: PA=PB
证明:∵ MN⊥AB
∴ ∠PCA= ∠PCB =90°
在ΔPAC和ΔPBC中:
AC=BC
∠PCA= ∠PCB
PC=PC
∴ ΔPAC ≌ΔPBC(SAS)
∴ PA=PB
你能画图证明吗?
*
*
线段的垂直平分线的性质定理:
线段的垂直平分线上的点到这条线段的两个端点的距离相等。
几何语言——
∵MN⊥AB MN平分AB或AN=BN
∴PA=PB
N
A
B
P
M
C
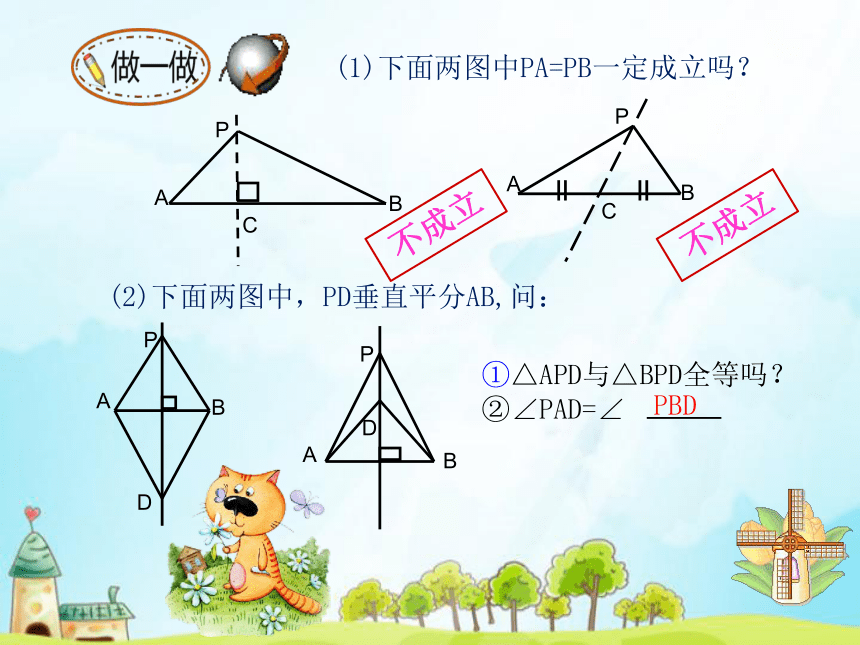
(1)下面两图中PA=PB一定成立吗?
P
A
B
C
P
A
B
C
(2)下面两图中,PD垂直平分AB,问:
P
A
B
D
P
A
B
D
①△APD与△BPD全等吗?
②∠PAD=∠
PBD
不成立
不成立
*
*
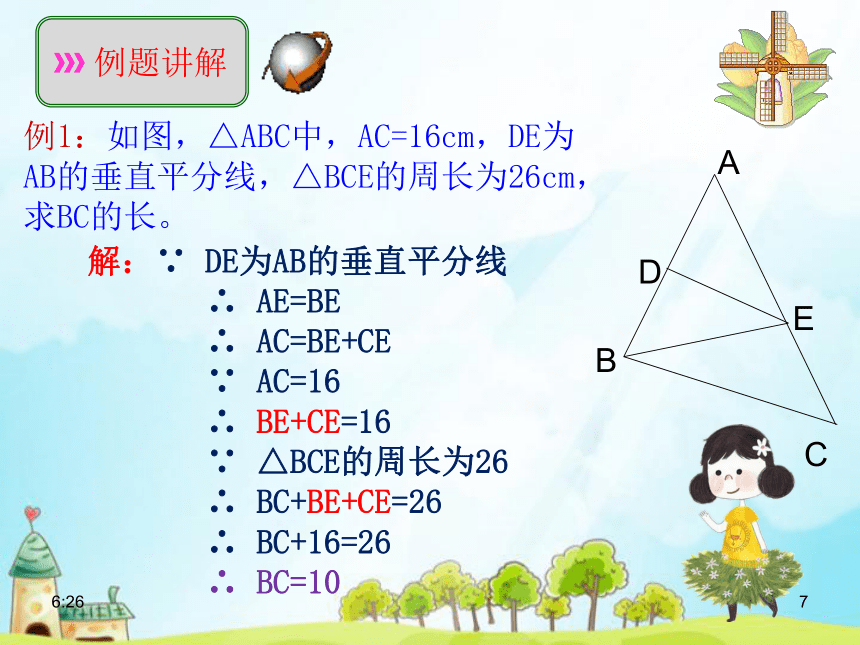
例1:如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,求BC的长。
A
E
D
B
C
解:∵ DE为AB的垂直平分线
∴ AE=BE
∴ AC=BE+CE
∵ AC=16
∴ BE+CE=16
∵ △BCE的周长为26
∴ BC+BE+CE=26
∴ BC+16=26
∴ BC=10
例题讲解
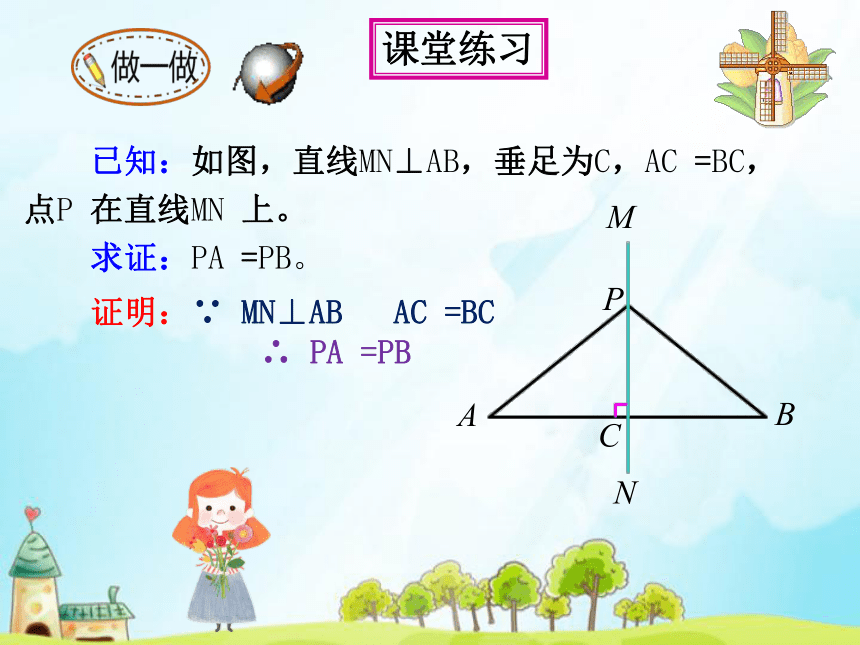
已知:如图,直线MN⊥AB,垂足为C,AC =BC,
点P 在直线MN 上。
求证:PA =PB。
A
B
P
C
M
N
证明:∵ MN⊥AB AC =BC
∴ PA =PB
课堂练习
*
*
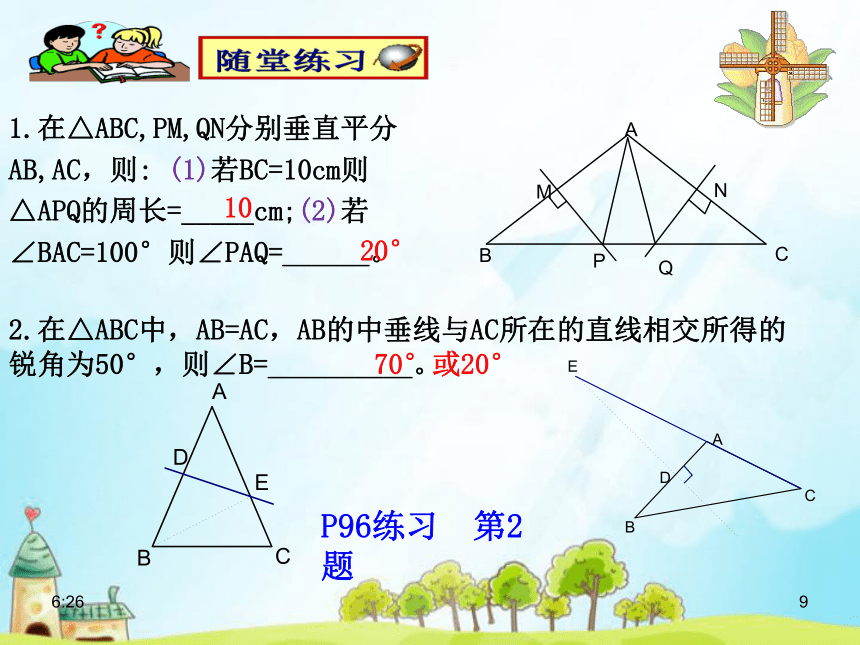
1.在△ABC,PM,QN分别垂直平分AB,AC,则: (1)若BC=10cm则△APQ的周长=_____cm;(2)若∠BAC=100°则∠PAQ=______。
10
20°
2.在△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为50°,则∠B=__________。
70°或20°
P96练习 第2题
*
*
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线上的点到这条线段两个端点的距离相等。
逆命题
思考:线段的垂直平分线的逆命题应如何表述
你能证明这个结论吗?
*
*
A
B
P
C
已知:如图, PA=PB
求证: 点P在线段AB的垂直平分线上
证明:过点P作PC⊥AB于C
则∠PCA=∠PCB=90°
∴ΔPAC和ΔPBC是RtΔ
在RtΔPAC和RtΔPBC中:
PC=PB
PC=PC
∴ΔPAC ≌ΔPBC(HL)
∴AC=BC
∴直线PC垂直平分线段AB
即:点P在线段AB的垂直平分线上
你能画图证明吗?
*
*
线段的垂直平分线的判定定理:
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。
几何语言:
∵ PA=PB
∴点P在线段AB的垂直平分线上
N
A
B
P
M
C
条件
结论
性质定理
逆命题
在线段的垂直平分线上有一点。
该点到线段两端的距离相等。
有一点到线段的两个端点距离相等
这点在线段的垂直平分线上
*
*
P
B
D
C
①若PB=PC,则PD是线段BC的垂直平分线( )
②若BD⊥CD,则PD是线段BC的垂直平分线( )
③若PB=PC,DB=DC,则PD垂直平分BC ( )
④若PD是线段BC的垂直平分线,则BP=CP ( )
判 断
X
√
X
√
课堂练习
*
*
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线上的点到这条线段两个端点的距离相等。
逆命题
逆定理可以用来证明
点在直线上
性质定理可以用来证明
两条线段相等
强调:
证明:∵ AB =AC
∴ 点A 在BC 的垂直平分线
∵ MB =MC
∴ 点M 在BC 的垂直平分线上
∴ 直线AM 是线段BC 的垂直平分线
例2:如图,AB =AC,MB =MC。
求证:直线AM 是线段BC 的垂直平分线。
A
B
C
D
M
(两点确定一条直线)
例题讲解
P96练习 第3题
*
*
证明:∵ 点P在线段AB的垂直平分线MN上
∴ PA=PB(?)
同理:PB=PC
∴ PA=PB=PC
∵ PA=PC
∴ 点P在AC边的垂直平分线上
B
A
C
M
N
M’
N’
P
从这里我们可以看到,要想证明三角形三条垂直平分线交于一点,只需证明其中的两条垂直平分线的交点一定在第三条垂直平分线上就可以了。
思考:如图,△ABC中,边AB、BC的垂直平分线交于点P。
1.求证:PA=PB=PC。
2.点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
*
*
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
P
P96练习 第1题
回归生活
∴ 点P即为所求。
【提示】学校在连接任意两点的两条线段的垂直平分线的交点处。
二、方法:
本节课你有何收获与疑惑?
线段垂直平分线性质定理
线段垂直平分线上的点到线段两端点的距离相等。
线段垂直平分线性质定理的逆定理
到线段两端距离相等的点在线段的垂直平分线上。
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
一、知识方面:
2. 转化思想
1. 数形结合
三、思想:
1、操作—猜想—验证—归纳—应用;
2、 利用数学解决生活中的实际问题。
小结 提高
课堂总结
*
*
P99习题 第5、6题
P104复习题 第10、15、16题
课后作业
基 础 过 关
1.若P是△ABC所在平面内的点,且PA=PB=PC,则下列说法正确的是( )
A. 点P是△ABC三边垂直平分线的交点
B. 点P是△ABC三条角平分线的交点
C. 点P是△ABC三边上高的交点
D. 点P是△ABC三边中线的交点
A
2.如图,在△ABC中,AB=AC,∠ABC=65°,
DE是AB的垂直平分线,则∠CBE=______。
解:∵在△ABC中 AB=AC ∠ABC=65°
∴∠ABC=∠C=65°
∴∠A=180°-∠ABC-∠C=50°
∵DE是AB的垂直平分线,
∴AE=BE,∴∠ABE=∠A=50°
∴∠CBE=∠ABC-∠ABE=15°
15°
谢谢欣赏
THANK YOU FOR LISTENING
*
*
13.5.2 线段垂直平分线
第13章 逆命题与逆定理
创设情境
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
*
*
1、什么叫线段垂直平分线?
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2、线段垂直平分线有什么性质?
线段垂直平分线上的点与这条线段的两个端点的距离相等 。
你能画图证明吗?
知识回顾
*
*
A
B
P
M
N
C
已知:如图,直线MN⊥AB,垂足为C,
且AC=CB,点P在MN上。
求证: PA=PB
证明:∵ MN⊥AB
∴ ∠PCA= ∠PCB =90°
在ΔPAC和ΔPBC中:
AC=BC
∠PCA= ∠PCB
PC=PC
∴ ΔPAC ≌ΔPBC(SAS)
∴ PA=PB
你能画图证明吗?
*
*
线段的垂直平分线的性质定理:
线段的垂直平分线上的点到这条线段的两个端点的距离相等。
几何语言——
∵MN⊥AB MN平分AB或AN=BN
∴PA=PB
N
A
B
P
M
C
(1)下面两图中PA=PB一定成立吗?
P
A
B
C
P
A
B
C
(2)下面两图中,PD垂直平分AB,问:
P
A
B
D
P
A
B
D
①△APD与△BPD全等吗?
②∠PAD=∠
PBD
不成立
不成立
*
*
例1:如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,求BC的长。
A
E
D
B
C
解:∵ DE为AB的垂直平分线
∴ AE=BE
∴ AC=BE+CE
∵ AC=16
∴ BE+CE=16
∵ △BCE的周长为26
∴ BC+BE+CE=26
∴ BC+16=26
∴ BC=10
例题讲解
已知:如图,直线MN⊥AB,垂足为C,AC =BC,
点P 在直线MN 上。
求证:PA =PB。
A
B
P
C
M
N
证明:∵ MN⊥AB AC =BC
∴ PA =PB
课堂练习
*
*
1.在△ABC,PM,QN分别垂直平分AB,AC,则: (1)若BC=10cm则△APQ的周长=_____cm;(2)若∠BAC=100°则∠PAQ=______。
10
20°
2.在△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为50°,则∠B=__________。
70°或20°
P96练习 第2题
*
*
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线上的点到这条线段两个端点的距离相等。
逆命题
思考:线段的垂直平分线的逆命题应如何表述
你能证明这个结论吗?
*
*
A
B
P
C
已知:如图, PA=PB
求证: 点P在线段AB的垂直平分线上
证明:过点P作PC⊥AB于C
则∠PCA=∠PCB=90°
∴ΔPAC和ΔPBC是RtΔ
在RtΔPAC和RtΔPBC中:
PC=PB
PC=PC
∴ΔPAC ≌ΔPBC(HL)
∴AC=BC
∴直线PC垂直平分线段AB
即:点P在线段AB的垂直平分线上
你能画图证明吗?
*
*
线段的垂直平分线的判定定理:
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。
几何语言:
∵ PA=PB
∴点P在线段AB的垂直平分线上
N
A
B
P
M
C
条件
结论
性质定理
逆命题
在线段的垂直平分线上有一点。
该点到线段两端的距离相等。
有一点到线段的两个端点距离相等
这点在线段的垂直平分线上
*
*
P
B
D
C
①若PB=PC,则PD是线段BC的垂直平分线( )
②若BD⊥CD,则PD是线段BC的垂直平分线( )
③若PB=PC,DB=DC,则PD垂直平分BC ( )
④若PD是线段BC的垂直平分线,则BP=CP ( )
判 断
X
√
X
√
课堂练习
*
*
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线上的点到这条线段两个端点的距离相等。
逆命题
逆定理可以用来证明
点在直线上
性质定理可以用来证明
两条线段相等
强调:
证明:∵ AB =AC
∴ 点A 在BC 的垂直平分线
∵ MB =MC
∴ 点M 在BC 的垂直平分线上
∴ 直线AM 是线段BC 的垂直平分线
例2:如图,AB =AC,MB =MC。
求证:直线AM 是线段BC 的垂直平分线。
A
B
C
D
M
(两点确定一条直线)
例题讲解
P96练习 第3题
*
*
证明:∵ 点P在线段AB的垂直平分线MN上
∴ PA=PB(?)
同理:PB=PC
∴ PA=PB=PC
∵ PA=PC
∴ 点P在AC边的垂直平分线上
B
A
C
M
N
M’
N’
P
从这里我们可以看到,要想证明三角形三条垂直平分线交于一点,只需证明其中的两条垂直平分线的交点一定在第三条垂直平分线上就可以了。
思考:如图,△ABC中,边AB、BC的垂直平分线交于点P。
1.求证:PA=PB=PC。
2.点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
*
*
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
P
P96练习 第1题
回归生活
∴ 点P即为所求。
【提示】学校在连接任意两点的两条线段的垂直平分线的交点处。
二、方法:
本节课你有何收获与疑惑?
线段垂直平分线性质定理
线段垂直平分线上的点到线段两端点的距离相等。
线段垂直平分线性质定理的逆定理
到线段两端距离相等的点在线段的垂直平分线上。
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
一、知识方面:
2. 转化思想
1. 数形结合
三、思想:
1、操作—猜想—验证—归纳—应用;
2、 利用数学解决生活中的实际问题。
小结 提高
课堂总结
*
*
P99习题 第5、6题
P104复习题 第10、15、16题
课后作业
基 础 过 关
1.若P是△ABC所在平面内的点,且PA=PB=PC,则下列说法正确的是( )
A. 点P是△ABC三边垂直平分线的交点
B. 点P是△ABC三条角平分线的交点
C. 点P是△ABC三边上高的交点
D. 点P是△ABC三边中线的交点
A
2.如图,在△ABC中,AB=AC,∠ABC=65°,
DE是AB的垂直平分线,则∠CBE=______。
解:∵在△ABC中 AB=AC ∠ABC=65°
∴∠ABC=∠C=65°
∴∠A=180°-∠ABC-∠C=50°
∵DE是AB的垂直平分线,
∴AE=BE,∴∠ABE=∠A=50°
∴∠CBE=∠ABC-∠ABE=15°
15°
谢谢欣赏
THANK YOU FOR LISTENING
