13.5.3 角平分线 课件(共21张PPT)
文档属性
| 名称 | 13.5.3 角平分线 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 06:04:50 | ||
图片预览




文档简介
(共21张PPT)
13.5.3 角平分线
第13章 逆命题与逆定理
华东师大版第13章 全等三角形
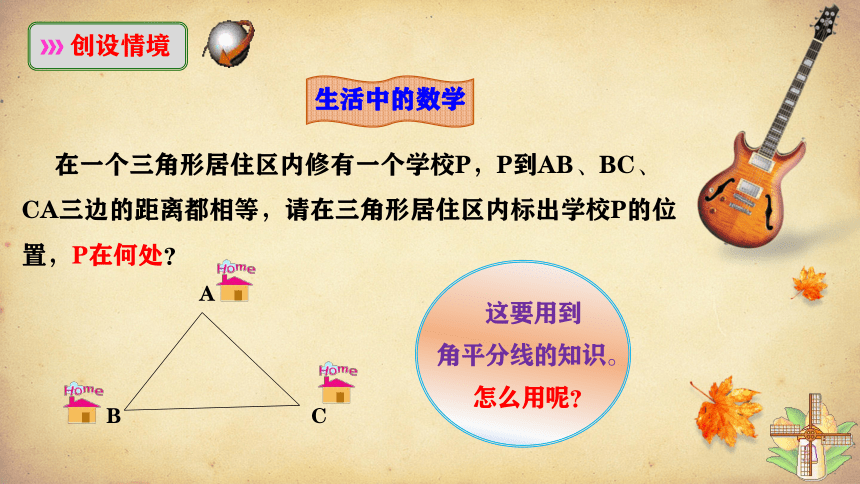
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
A
B
C
这要用到
角平分线的知识。
怎么用呢?
生活中的数学
创设情境
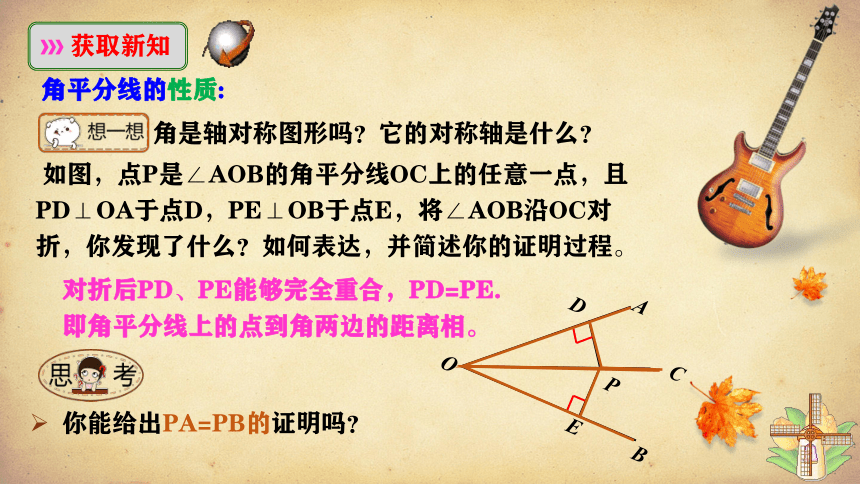
角平分线的性质:
如图,点P是∠AOB的角平分线OC上的任意一点,且PD⊥OA于点D,PE⊥OB于点E,将∠AOB沿OC对折,你发现了什么?如何表达,并简述你的证明过程。
对折后PD、PE能够完全重合,PD=PE.
即角平分线上的点到角两边的距离相。
角是轴对称图形吗?它的对称轴是什么?
D
P
A
C
B
E
O
你能给出PA=PB的证明吗?
获取新知
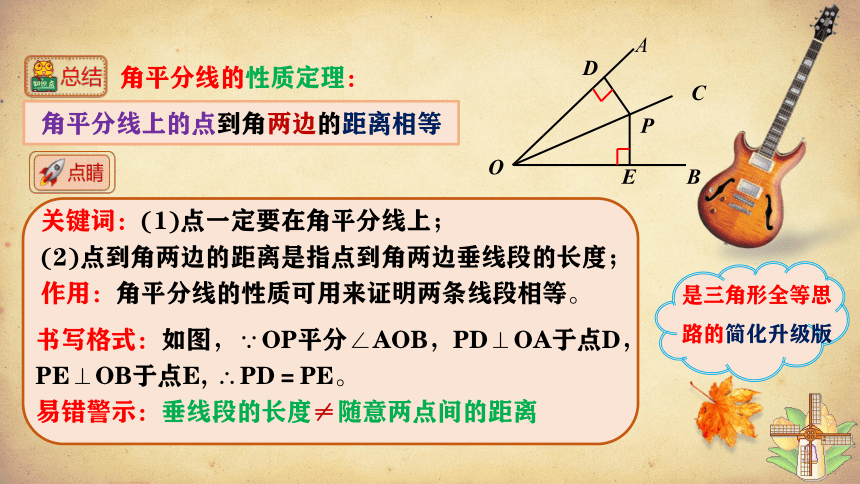
角平分线上的点到角两边的距离相等
书写格式:如图,∵OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E, ∴PD=PE。
易错警示:垂线段的长度≠随意两点间的距离
D
P
A
C
B
E
O
关键词:(1)点一定要在角平分线上;
(2)点到角两边的距离是指点到角两边垂线段的长度;
作用:角平分线的性质可用来证明两条线段相等。
是三角形全等思路的简化升级版
角平分线的性质定理:
角平分线性质定理的逆定理
写出性质定理及其逆命题的条件和结论,你有什么发现?
条 件 结 论
性质定理
逆命题
一个点在角的平分线上
这个点到这个角两边的距离相等
一个点到角两边的距离相等
这个点在这个角的平分线上
这个逆命题是否是一个真命题?你能证明吗?
角平分线的性质定理,条件和结论反过来会有什么结果呢?
逆命题 如果一个点到角两边的距离相等,那么这个点在这个角的平分线上。
分析:只需证明∠AOP和∠BOP所在的Rt△PDO和Rt△PEO全等。
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE
求证:点P在∠AOB的角平分线上
B
A
D
O
P
E
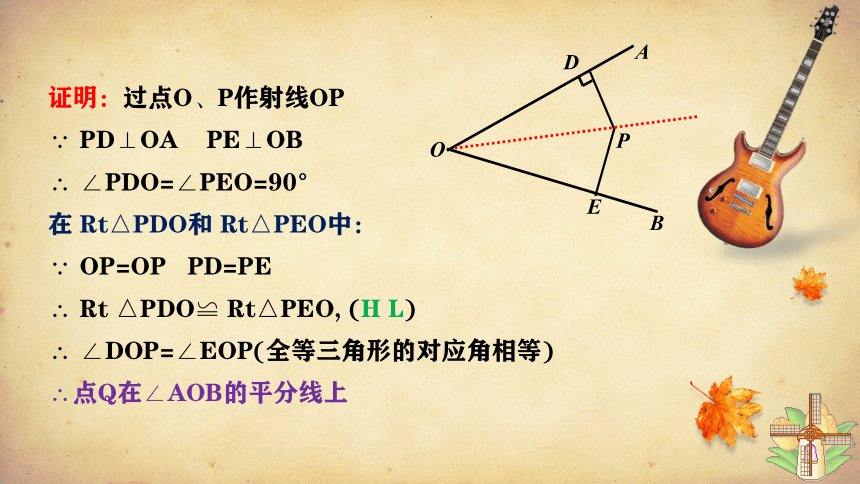
证明:过点O、P作射线OP
∵ PD⊥OA PE⊥OB
∴ ∠PDO=∠PEO=90°
在 Rt△PDO和 Rt△PEO中:
∵ OP=OP PD=PE
∴ Rt △PDO≌ Rt△PEO, (H L)
∴ ∠DOP=∠EOP(全等三角形的对应角相等)
∴点Q在∠AOB的平分线上
B
A
D
O
P
E
条件:点到角两边距离相等
结论:点在角平分线上
(1)书写格式:如图:
∵PD⊥OA PE⊥OB PD=PE
∴点P在∠AOB的平分线上(或∠AOC=∠BOC)
(2)作用:可以证明两个角相等或一条射线是角的平分线
角平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上
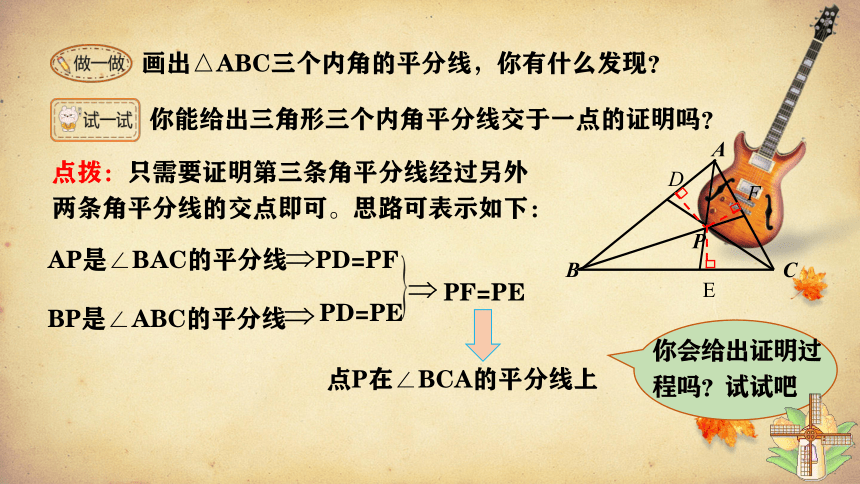
画出△ABC三个内角的平分线,你有什么发现?
点拨:只需要证明第三条角平分线经过另外两条角平分线的交点即可。思路可表示如下:
AP是∠BAC的平分线
BP是∠ABC的平分线
PD=PF
PD=PE
PF=PE
点P在∠BCA的平分线上
A
B
C
P
D
F
你会给出证明过程吗?试试吧
你能给出三角形三个内角平分线交于一点的证明吗?
E
例1 如图,在△ABC中,∠C=90°,AD平分∠CAB,
DE⊥AB于E,F在AC上,BE=FC,
求证:BD=DF
证明:∵ AD平分∠CAB DE⊥AB于E ∠C=90°
∴ DE=DC
在Rt△BDE和Rt△FDC中:
ED=CD
BE=FC
∴ Rt△BDE≌Rt△FDC(HL)
∴ BD=DF
例题讲解
在证明两条线段相等时,若两条线段分别在两个三角形中,可考虑使用三角形全等或角平分线的性质,若条件中有垂直和角平分线,则优先考虑使用角平分线的性质。
运用角平分线的性质证明线段相等时,不需要利用三角形全等。
例2 如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D。
求证:AD平分∠BAC
分析:要证AD平分∠BAC,已知条件中有两个垂直,即有点到角的两边的距离,再证这两个距离相等即可证明结论,证这两条垂线段相等,可通过证明△BDE和△CDF全等来完成。
例题讲解
证明:∵ DF⊥AC DE⊥AB
∴ ∠DEB=∠DFC=90°
在△BDE和△CDF中:
∠BDE=∠CDF
∠DEB=∠DFC
BE=CF
∴ △BDE≌△CDF(AAS)
∴ DE=DF
∵ DF⊥AC于点F DE⊥AB于点E
∴ AD平分∠BAC
证明角平分线的方法思路 :
从数量上证明被角平分线 分成的两个角相等。
从形上证明角的内部的点到角两边的距离相等,即只需从要证的线上的某一点向角的两边作垂 线段,再证明垂线段相等即可。这样把证“某线是角的平分线”的问题转化为证“垂线段相等”的问题,体现了转化思想。
角平分线的性质及判定
性质定理:角平分线上的点到角两边的距离相等.
判定定理:角的内部到角两边距离相等的点在角的平分线上.
三角形三条角平分线交于内部一点
课堂总结
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA QE⊥OB QD=QE
∴点Q在∠AOB的平分线上
角的平分线上的点到角的两边的距离相等。
用法:∵ QD⊥OA QE⊥OB OQ平分∠AOB
∴ QD=QE
1.角平分线的性质:
2.角平分线的判定:
课堂总结
课后作业P104习题第8、9题P99练习 第4、5题1.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长是( )A.2 B.3C.4 D.6D 基 础 过 关2.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )A.PC=PDB.∠CPO=∠DOPC.∠CPO=∠DPOD.OC=ODB 基 础 过 关C 基 础 过 关谢谢欣赏THANK YOU FOR LISTENING
13.5.3 角平分线
第13章 逆命题与逆定理
华东师大版第13章 全等三角形
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
A
B
C
这要用到
角平分线的知识。
怎么用呢?
生活中的数学
创设情境
角平分线的性质:
如图,点P是∠AOB的角平分线OC上的任意一点,且PD⊥OA于点D,PE⊥OB于点E,将∠AOB沿OC对折,你发现了什么?如何表达,并简述你的证明过程。
对折后PD、PE能够完全重合,PD=PE.
即角平分线上的点到角两边的距离相。
角是轴对称图形吗?它的对称轴是什么?
D
P
A
C
B
E
O
你能给出PA=PB的证明吗?
获取新知
角平分线上的点到角两边的距离相等
书写格式:如图,∵OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E, ∴PD=PE。
易错警示:垂线段的长度≠随意两点间的距离
D
P
A
C
B
E
O
关键词:(1)点一定要在角平分线上;
(2)点到角两边的距离是指点到角两边垂线段的长度;
作用:角平分线的性质可用来证明两条线段相等。
是三角形全等思路的简化升级版
角平分线的性质定理:
角平分线性质定理的逆定理
写出性质定理及其逆命题的条件和结论,你有什么发现?
条 件 结 论
性质定理
逆命题
一个点在角的平分线上
这个点到这个角两边的距离相等
一个点到角两边的距离相等
这个点在这个角的平分线上
这个逆命题是否是一个真命题?你能证明吗?
角平分线的性质定理,条件和结论反过来会有什么结果呢?
逆命题 如果一个点到角两边的距离相等,那么这个点在这个角的平分线上。
分析:只需证明∠AOP和∠BOP所在的Rt△PDO和Rt△PEO全等。
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE
求证:点P在∠AOB的角平分线上
B
A
D
O
P
E
证明:过点O、P作射线OP
∵ PD⊥OA PE⊥OB
∴ ∠PDO=∠PEO=90°
在 Rt△PDO和 Rt△PEO中:
∵ OP=OP PD=PE
∴ Rt △PDO≌ Rt△PEO, (H L)
∴ ∠DOP=∠EOP(全等三角形的对应角相等)
∴点Q在∠AOB的平分线上
B
A
D
O
P
E
条件:点到角两边距离相等
结论:点在角平分线上
(1)书写格式:如图:
∵PD⊥OA PE⊥OB PD=PE
∴点P在∠AOB的平分线上(或∠AOC=∠BOC)
(2)作用:可以证明两个角相等或一条射线是角的平分线
角平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上
画出△ABC三个内角的平分线,你有什么发现?
点拨:只需要证明第三条角平分线经过另外两条角平分线的交点即可。思路可表示如下:
AP是∠BAC的平分线
BP是∠ABC的平分线
PD=PF
PD=PE
PF=PE
点P在∠BCA的平分线上
A
B
C
P
D
F
你会给出证明过程吗?试试吧
你能给出三角形三个内角平分线交于一点的证明吗?
E
例1 如图,在△ABC中,∠C=90°,AD平分∠CAB,
DE⊥AB于E,F在AC上,BE=FC,
求证:BD=DF
证明:∵ AD平分∠CAB DE⊥AB于E ∠C=90°
∴ DE=DC
在Rt△BDE和Rt△FDC中:
ED=CD
BE=FC
∴ Rt△BDE≌Rt△FDC(HL)
∴ BD=DF
例题讲解
在证明两条线段相等时,若两条线段分别在两个三角形中,可考虑使用三角形全等或角平分线的性质,若条件中有垂直和角平分线,则优先考虑使用角平分线的性质。
运用角平分线的性质证明线段相等时,不需要利用三角形全等。
例2 如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D。
求证:AD平分∠BAC
分析:要证AD平分∠BAC,已知条件中有两个垂直,即有点到角的两边的距离,再证这两个距离相等即可证明结论,证这两条垂线段相等,可通过证明△BDE和△CDF全等来完成。
例题讲解
证明:∵ DF⊥AC DE⊥AB
∴ ∠DEB=∠DFC=90°
在△BDE和△CDF中:
∠BDE=∠CDF
∠DEB=∠DFC
BE=CF
∴ △BDE≌△CDF(AAS)
∴ DE=DF
∵ DF⊥AC于点F DE⊥AB于点E
∴ AD平分∠BAC
证明角平分线的方法思路 :
从数量上证明被角平分线 分成的两个角相等。
从形上证明角的内部的点到角两边的距离相等,即只需从要证的线上的某一点向角的两边作垂 线段,再证明垂线段相等即可。这样把证“某线是角的平分线”的问题转化为证“垂线段相等”的问题,体现了转化思想。
角平分线的性质及判定
性质定理:角平分线上的点到角两边的距离相等.
判定定理:角的内部到角两边距离相等的点在角的平分线上.
三角形三条角平分线交于内部一点
课堂总结
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA QE⊥OB QD=QE
∴点Q在∠AOB的平分线上
角的平分线上的点到角的两边的距离相等。
用法:∵ QD⊥OA QE⊥OB OQ平分∠AOB
∴ QD=QE
1.角平分线的性质:
2.角平分线的判定:
课堂总结
课后作业P104习题第8、9题P99练习 第4、5题1.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长是( )A.2 B.3C.4 D.6D 基 础 过 关2.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )A.PC=PDB.∠CPO=∠DOPC.∠CPO=∠DPOD.OC=ODB 基 础 过 关C 基 础 过 关谢谢欣赏THANK YOU FOR LISTENING
