13.全等三角形复习 课件(共16张PPT)
文档属性
| 名称 | 13.全等三角形复习 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 06:00:26 | ||
图片预览





文档简介
(共16张PPT)
*
*
*
*
全章知识结构图
图形的全等
三角形全等
(全等的判定)
S.S.S.
S.A.S.
A.S.A.
A.A.S.
H.L.(RtΔ)
命题与证明(定义、命题、公理、定理)
——证明
基本作图
画线段
画角
画垂线
画垂直平分线
画角平分线
*
*
1.什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2.全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
*
*
3.证明两个三角形全等的基本思路:
(1):已知两边:
找第三边
SSS
找夹角
SAS
(2):已知一边一角:
已知一边和它的邻角
找是否有直角
HL
已知一边和它的对角
找这边的另一个邻角 ASA
找这个角的另一个边 SAS
找这边的对角 AAS
找一角 AAS
已知角是直角,找一边 HL
(3):已知两角:
找两角的夹边 ASA
找夹边外的任意边 AAS
*
*
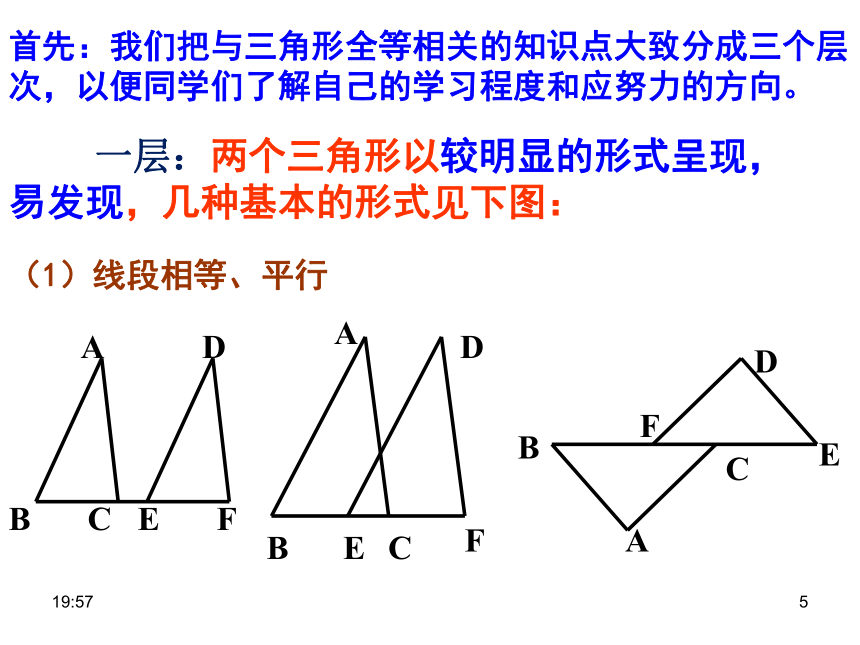
(1)线段相等、平行
A
E
D
C
F
B
F
C
D
B
A
E
F
C
A
B
D
E
首先:我们把与三角形全等相关的知识点大致分成三个层次,以便同学们了解自己的学习程度和应努力的方向。
一层:两个三角形以较明显的形式呈现,易发现,几种基本的形式见下图:
*
*
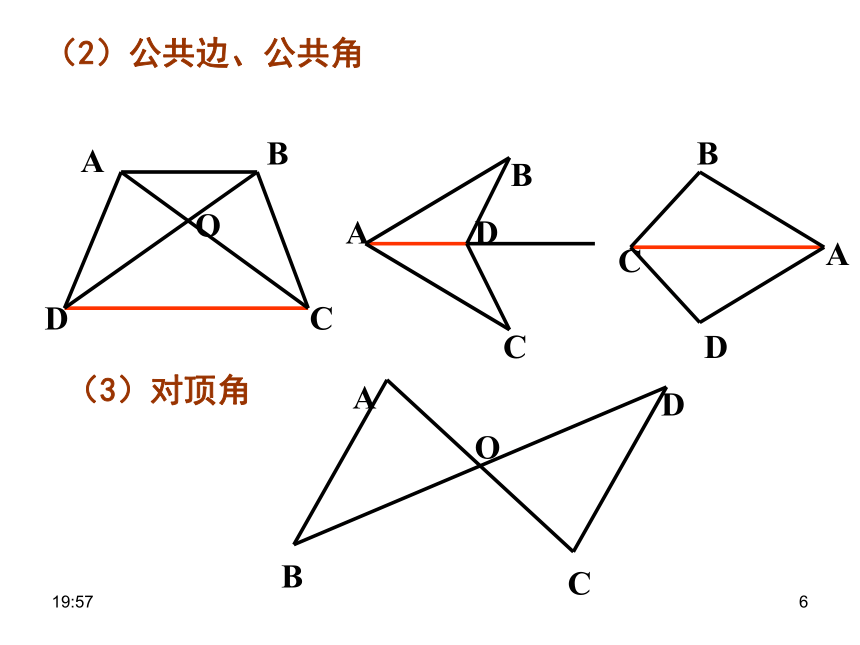
(2)公共边、公共角
A
D
C
B
A
D
C
B
D
B
C
A
O
(3)对顶角
A
O
C
D
B
*
*
例1:如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:∠A= ∠D
D
B
A
E
F
C
证明:∵BE=CF
∴BE+EC=CF+EC
即BC=EF
∴△ABC≌△DEF (S. S. S)
∴∠A= ∠D
*
*
例2:如图,点A、F、E、C在同一直线上,AF=CE,BE = DF,BE∥DF,求证:AB∥CD。
证明:
∥
∥
AE=CF
BE=DF
≌
(S.A.S.)
*
*
证明:
D
C
E
A
B
∠B=∠D
∠BAC=∠DAE
≌
(A.S.A)
二层:两个三角形的呈现不明显,有重叠的部分,需从已知条件出发找需要的三角形(可用阴影标出)
例3:如图,已知,AB=AD,∠B=∠D,∠BAE=∠DAC,求证∠C=∠E
*
*
例4:如图,∠A=∠D=90。,BD于AC相交于点O,且BD=AC。求证:OB=OC
B
O
D
A
C
1
2
证明:∵ ∠A=∠D=90。
∴△ABC和△DCB是Rt △
在Rt△ABC和Rt△DCB中
∵
BD=AC
BC=BC
∴Rt△ABC≌Rt△DCB(H. L)
∴∠1=∠2
∴OB=OC(等角对等边)
*
*
例5:如图,AD⊥BC,CE⊥AB,垂足为D、E,AD交CE于点F,AD=CE。求证:AF=CF
A
B
D
F
E
C
1
2
证明: ∵AD⊥BC,CE⊥AB
∴∠BEC=∠BDA=90。
在△BAD和△BCE中
∵ ∠BEC=∠BDA=90。
∠B=∠B
AD=CE
∴ △BAD≌△BCE(A.A.S)
∴ BA=BC,BE=BD
∴ BA-BE=BC-BD
即EA=DC
(接下来证明△FAE≌△FCD(A.A.S) )
三层:题目的条件、结论都需要同学们全面考虑,综合所学的知识点并能灵活运用.
*
*
例6:如图,AB、CD相交于E,且AB=CD,AC=DB。求证:EA=ED
证明: 连接BC
在△ABC和△DCB中
∵ AC=DB
AB=CD
BC=BC
∴ △ABC≌△DCB(S.S.S)
∴ ∠A=∠D
(接下来证明△AEC≌△DEB(A.A.S) )
A
B
D
E
C
1
2
*
*
例7.已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上。求证:BE=AD
E
D
C
A
B
证明:
∵ △ABC和△ECD是正三角形
∴ AC=BC , DC=EC
∠BCA=∠DCE=60°
∴∠BCA+∠ACE=∠DCE+∠ACE
即:∠BCE=∠DCA
在△ACD和△BCE中
AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
*
*
例8:如图,已知E在AB上,∠1=∠2,∠3=∠4.
求证:AC=AD
4
3
2
1
E
D
C
B
A
证明:
在△EBC和△EBD中
∠1=∠2
∠3=∠4
EB=EB
∴ △EBC≌△EBD (AAS)
∴ BC=BD
在△ABC和△ABD中
AB=AB
∠1=∠2
BC=BD
∴ △ABC≌△ABD (SAS)
∴ AC=AD
*
*
思考:如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
A
C
E
B
D
要证明两条线段的和与一条线段相等时常用的两种方法:
1、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
2、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补)
*
*
总 结
学习全等三角形应注意以下几个问题:
1.要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;
2.表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
3.要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
4.时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”等。
*
*
*
*
全章知识结构图
图形的全等
三角形全等
(全等的判定)
S.S.S.
S.A.S.
A.S.A.
A.A.S.
H.L.(RtΔ)
命题与证明(定义、命题、公理、定理)
——证明
基本作图
画线段
画角
画垂线
画垂直平分线
画角平分线
*
*
1.什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2.全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
*
*
3.证明两个三角形全等的基本思路:
(1):已知两边:
找第三边
SSS
找夹角
SAS
(2):已知一边一角:
已知一边和它的邻角
找是否有直角
HL
已知一边和它的对角
找这边的另一个邻角 ASA
找这个角的另一个边 SAS
找这边的对角 AAS
找一角 AAS
已知角是直角,找一边 HL
(3):已知两角:
找两角的夹边 ASA
找夹边外的任意边 AAS
*
*
(1)线段相等、平行
A
E
D
C
F
B
F
C
D
B
A
E
F
C
A
B
D
E
首先:我们把与三角形全等相关的知识点大致分成三个层次,以便同学们了解自己的学习程度和应努力的方向。
一层:两个三角形以较明显的形式呈现,易发现,几种基本的形式见下图:
*
*
(2)公共边、公共角
A
D
C
B
A
D
C
B
D
B
C
A
O
(3)对顶角
A
O
C
D
B
*
*
例1:如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:∠A= ∠D
D
B
A
E
F
C
证明:∵BE=CF
∴BE+EC=CF+EC
即BC=EF
∴△ABC≌△DEF (S. S. S)
∴∠A= ∠D
*
*
例2:如图,点A、F、E、C在同一直线上,AF=CE,BE = DF,BE∥DF,求证:AB∥CD。
证明:
∥
∥
AE=CF
BE=DF
≌
(S.A.S.)
*
*
证明:
D
C
E
A
B
∠B=∠D
∠BAC=∠DAE
≌
(A.S.A)
二层:两个三角形的呈现不明显,有重叠的部分,需从已知条件出发找需要的三角形(可用阴影标出)
例3:如图,已知,AB=AD,∠B=∠D,∠BAE=∠DAC,求证∠C=∠E
*
*
例4:如图,∠A=∠D=90。,BD于AC相交于点O,且BD=AC。求证:OB=OC
B
O
D
A
C
1
2
证明:∵ ∠A=∠D=90。
∴△ABC和△DCB是Rt △
在Rt△ABC和Rt△DCB中
∵
BD=AC
BC=BC
∴Rt△ABC≌Rt△DCB(H. L)
∴∠1=∠2
∴OB=OC(等角对等边)
*
*
例5:如图,AD⊥BC,CE⊥AB,垂足为D、E,AD交CE于点F,AD=CE。求证:AF=CF
A
B
D
F
E
C
1
2
证明: ∵AD⊥BC,CE⊥AB
∴∠BEC=∠BDA=90。
在△BAD和△BCE中
∵ ∠BEC=∠BDA=90。
∠B=∠B
AD=CE
∴ △BAD≌△BCE(A.A.S)
∴ BA=BC,BE=BD
∴ BA-BE=BC-BD
即EA=DC
(接下来证明△FAE≌△FCD(A.A.S) )
三层:题目的条件、结论都需要同学们全面考虑,综合所学的知识点并能灵活运用.
*
*
例6:如图,AB、CD相交于E,且AB=CD,AC=DB。求证:EA=ED
证明: 连接BC
在△ABC和△DCB中
∵ AC=DB
AB=CD
BC=BC
∴ △ABC≌△DCB(S.S.S)
∴ ∠A=∠D
(接下来证明△AEC≌△DEB(A.A.S) )
A
B
D
E
C
1
2
*
*
例7.已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上。求证:BE=AD
E
D
C
A
B
证明:
∵ △ABC和△ECD是正三角形
∴ AC=BC , DC=EC
∠BCA=∠DCE=60°
∴∠BCA+∠ACE=∠DCE+∠ACE
即:∠BCE=∠DCA
在△ACD和△BCE中
AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
*
*
例8:如图,已知E在AB上,∠1=∠2,∠3=∠4.
求证:AC=AD
4
3
2
1
E
D
C
B
A
证明:
在△EBC和△EBD中
∠1=∠2
∠3=∠4
EB=EB
∴ △EBC≌△EBD (AAS)
∴ BC=BD
在△ABC和△ABD中
AB=AB
∠1=∠2
BC=BD
∴ △ABC≌△ABD (SAS)
∴ AC=AD
*
*
思考:如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
A
C
E
B
D
要证明两条线段的和与一条线段相等时常用的两种方法:
1、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
2、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补)
*
*
总 结
学习全等三角形应注意以下几个问题:
1.要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;
2.表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
3.要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
4.时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”等。
