14.1.1 直角三角形三边的关系
图片预览





文档简介
第14章 勾股定理
14.1.1 直角三角形三边的关系
——数形结合之美
1
创设情境
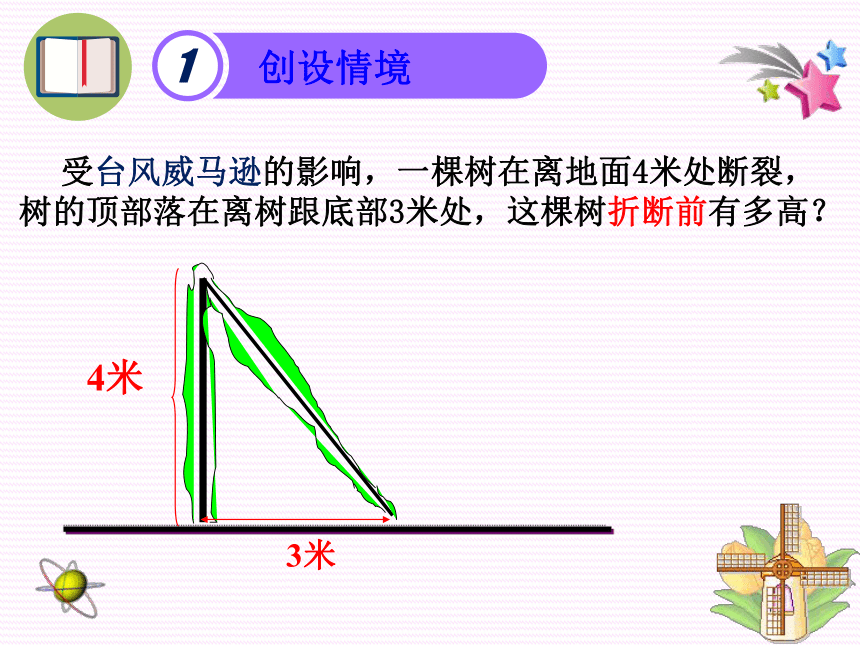
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
(图中每一格代表一平方厘米)
观察左图:
(1)正方形P的面积是 平方厘米。
(2)正方形Q的面积是 平方厘米。
(3)正方形R的面积是 平方厘米。
1
2
1
上面三个正方形的面积之间有什么关系?
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
2
知识探究
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
想一想
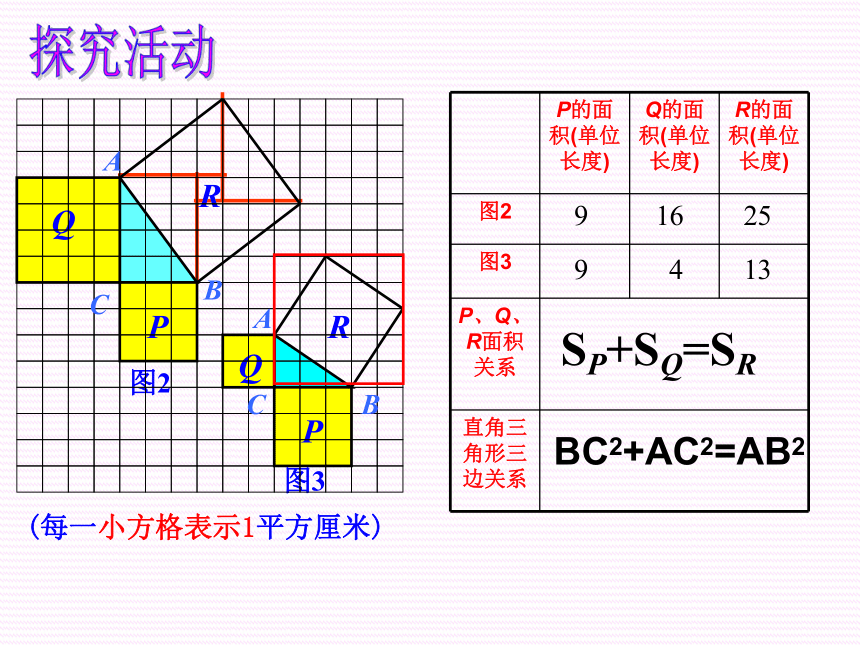
探究活动
P的面积(单位长度)
Q的面积(单位长度)
R的面积(单位长度)
图2
图3
P、Q、R面积关系
直角三角形三边关系
Q
P
R
图2
Q
P
R
图3
A
B
C
A
B
C
9
16
25
9
4
13
SP+SQ=SR
BC2+AC2=AB2
(每一小方格表示1平方厘米)
Q
P
R
图1-3
Q
P
R
图1-4
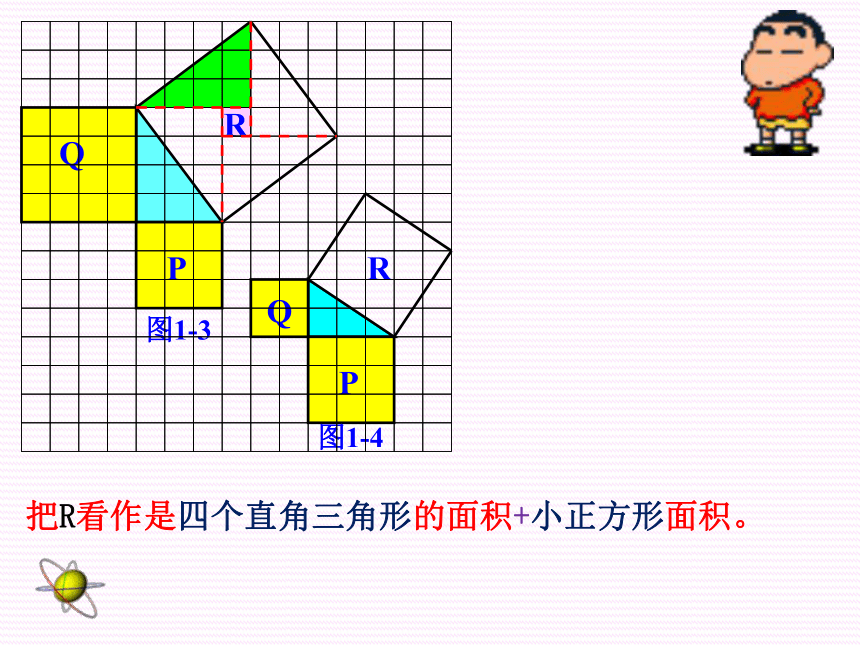
把R看作是四个直角三角形的面积+小正方形面积。
Q
P
R
图3
Q
P
R
图4
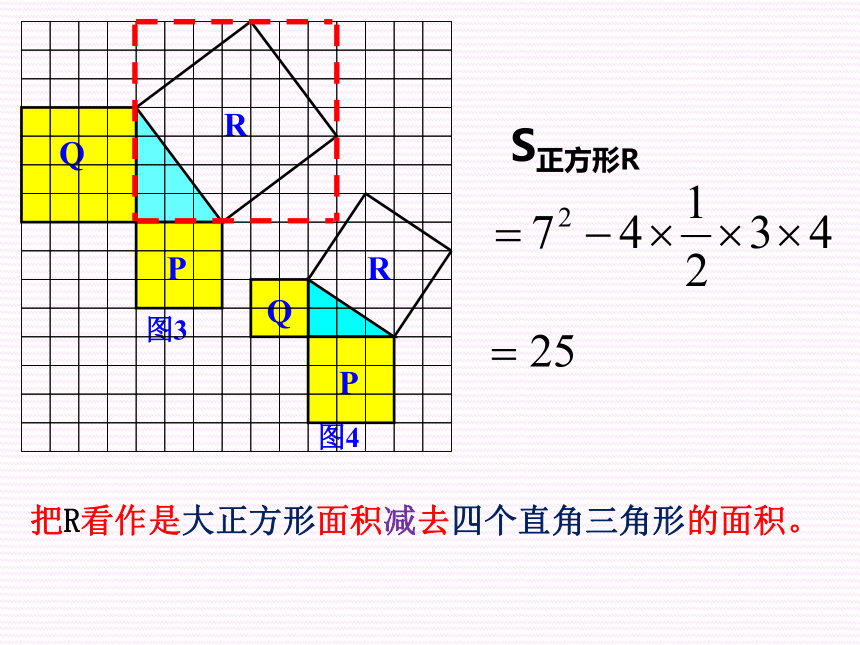
把R看作是大正方形面积减去四个直角三角形的面积。
S正方形R
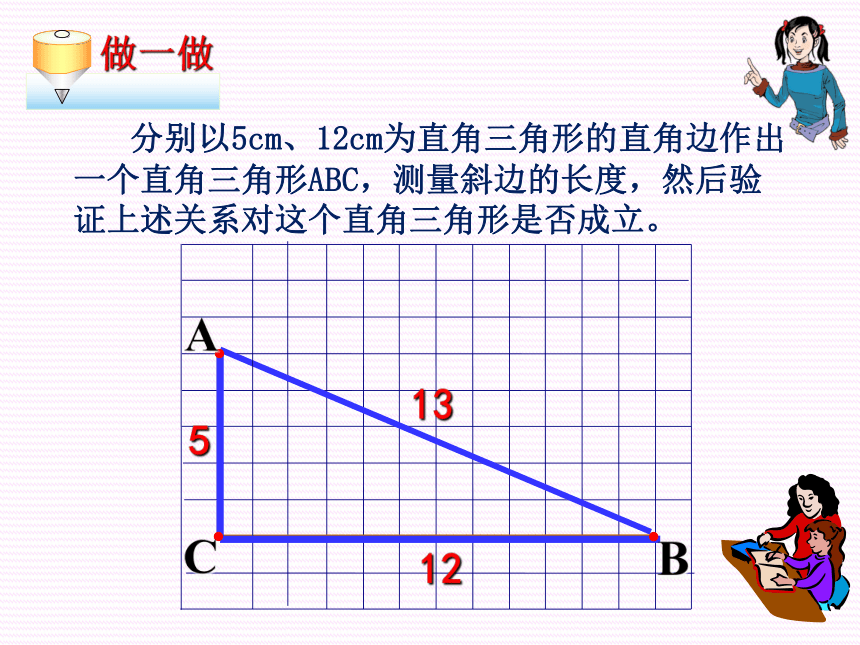
分别以5cm、12cm为直角三角形的直角边作出一个直角三角形ABC,测量斜边的长度,然后验证上述关系对这个直角三角形是否成立。
做一做
13
5
12
A
B
C
对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c(最长边),那么一定有:a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方。
A
B
C
b
c
几何语言:
在Rt△ABC中 (已知)
由勾股定理得:
∴a2+b2=c2(勾股定理)
勾股定理:
∟
注意:
1.运用前提:已知直角三角形和直角。
2.揭示了直角三角形三条边的关系;
3.运用中要注意直角与斜边的对应关系;
4.三边中最长的边就是斜边。
a
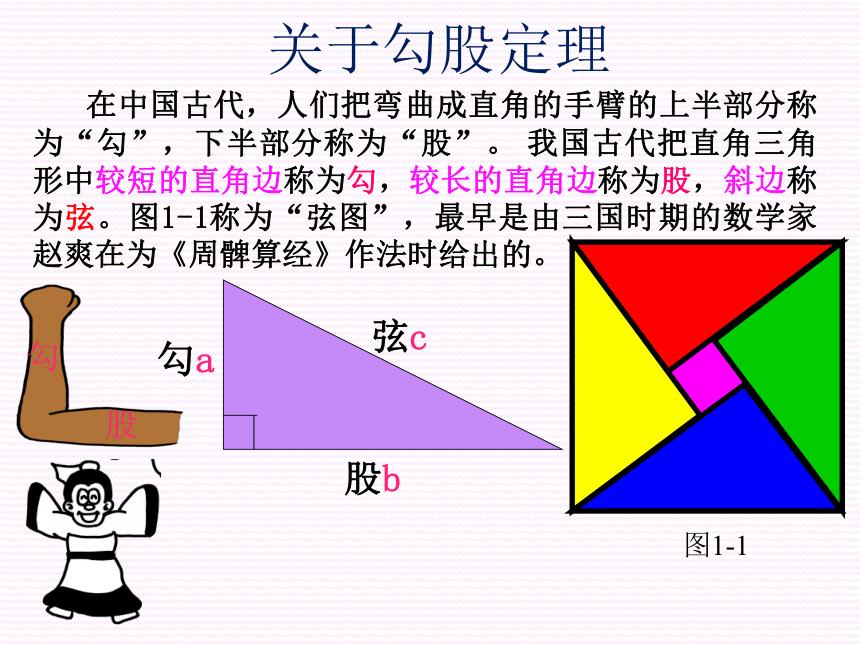
关于勾股定理
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。
弦c
股b
勾a
图1-1
勾
股
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” 。传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” 。在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
a
b
c
c2=a2 + b2
a2=c2 - b2
b2 =c2 -a2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方:
如果知道了直角三角形两边的长度,那么应用勾股定理可以求出第三边的长度
勾股定理的证明(一)
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 。人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
证明:
教材P141
b
a
c
勾股定理的证明(二)
a
b
c
a
b
c
a
b
c
最早是由1700多年前三国时期的数学家赵爽为《周髀算经》作注时给出的,他用面积法证明了勾股定理。
你能用面积法证明勾股定理吗?
弦
图
证明:
a
b
c
你能用两种方法表示这个小正方形(空白部分)的面积吗?
勾股定理的证明(三)
证明:
将上面弦图中的四个三角形
重新拼成右图形式。
3
例题讲解
例1:在Rt△ABC中,∠C=90°。
(1) 已知:a=3,b=4,求c;
(2) 已知:a=24,c=25,求b;
(3) 已知:c=13,b=5,求a;
a
b
c
C
B
解:(1)在Rt△ABC中:
设c的长为x,由勾股定理得:
82+ x2=172
即:x=????????????????????? 解得:x=15
∴ c=15
?
独立完成第2和3小题
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
y=0
应用知识回归生活
解:由题可得
答:这棵树折断前高9米。
1、求出下列直角三角形中未知边的长度。
6
x
25
24
8
X
试一试
2.判断题 ①△ABC的两边AB=5,AC=12,则BC=13 ( ) ②△ABC的a=6,b=8,则c=10 ( ) 3.填空题 在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____,斜边为上的高为______。
?
?
24
4.8
A
B
C
D
3
例题讲解
例2:如果一个直角三角形的两条边长分别是6厘米和8厘米,求第三边长。
解:当8为直角边时:
斜边长为:
当8为斜边长时:
另一条直角边为:
10
试一试:课本51页练习2题。
答:第三边的长是10或 。
例3:在直角△ABC中, ∠C=90°,a、b、c分别为∠A、∠B 、∠C的对边。
(1)若a=3, b=4,求c的长;(2)若a=5, c =12,求b的长
(3)若a:b=3:4,c=15,求a、b的长
3
例题讲解
1、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
?
A
试一试:
2.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解:在Rt△ABC中,由勾股定理得:
BC2=AB2-AC2
=2.52-2.42
=0.49
答:这时梯脚与墙的距离是0.7米。
试一试:
B
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
试一试:
例4 : 如图,将长为5.41米的梯子AC斜靠在墙上
,BC长为2.16米,求梯子上端A到墙的底端B的
距离AB。(精确到0.01米)
解:在Rt△ABC中:
BC=2.16 AC=5.41
由勾股定理得:
≈4.96(米)
3
例题讲解
答:梯子上端A到墙的底端B的
距离AB是4.96米。
3
例题讲解
例5:如图,为了求出湖两岸的A、B 两点之间的距离,一个观测者在点C 设桩,使⊿ABC 恰好为直角三角形。通过测量,得到 AC 长160米,BC 长128米。问从点A穿过湖到点 B 有多远?
解:在Rt△ABC中:
AC=160米 BC=128米
= 96(米)
答:从点A穿过湖到点B有96米。
由勾股定理得:
3
例题讲解
3
例题讲解
A
D
B
C
3
4
例6.已知∠ACB=90°,
CD⊥AB,AC=3,BC=4。
求CD的长。
∟
解:∵∠ACB=90°
∵∠ACB=90°,CD⊥AB,
注意:在直角三角形中两直角边的积等于斜边与其高的积。
例7:如图正三角形ABC的边长为6。
(1)求高AD的长;(2)求三角形ABC的面积。
A
B
C
D
∟
提示:过点A作AD垂直BC于D
勾股小常识:勾股数
1、 a?+b? =c?,满足(a,b,c)=1则a,b,c,为基本勾股数如:3、4、5;5、12、 13;7、24、25……;
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、18……;
3、若a,b,c是一组基本的勾股数,则a,b,c不能同时为奇数或同时为偶数;
4、一组勾股数中必有一个数是5的倍数;
5、2mn,m?-n?,m?+n?为勾股数组,m>n﹥0,m,n一奇一偶;
a
3
6
9
—
3n
b
4
8
16
—
4n
c
5
15
20
—
5n
10
12
12
勾股定理
如果直角三角形两直角边长分别为a、b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
4
课堂小结
同学们,
辛苦了,
欢迎领导同仁莅临指导
老
大
师
大
导
大
领
大
好
大
欢迎指导
14.1.1 直角三角形三边的关系
——数形结合之美
1
创设情境
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
(图中每一格代表一平方厘米)
观察左图:
(1)正方形P的面积是 平方厘米。
(2)正方形Q的面积是 平方厘米。
(3)正方形R的面积是 平方厘米。
1
2
1
上面三个正方形的面积之间有什么关系?
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
2
知识探究
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
想一想
探究活动
P的面积(单位长度)
Q的面积(单位长度)
R的面积(单位长度)
图2
图3
P、Q、R面积关系
直角三角形三边关系
Q
P
R
图2
Q
P
R
图3
A
B
C
A
B
C
9
16
25
9
4
13
SP+SQ=SR
BC2+AC2=AB2
(每一小方格表示1平方厘米)
Q
P
R
图1-3
Q
P
R
图1-4
把R看作是四个直角三角形的面积+小正方形面积。
Q
P
R
图3
Q
P
R
图4
把R看作是大正方形面积减去四个直角三角形的面积。
S正方形R
分别以5cm、12cm为直角三角形的直角边作出一个直角三角形ABC,测量斜边的长度,然后验证上述关系对这个直角三角形是否成立。
做一做
13
5
12
A
B
C
对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c(最长边),那么一定有:a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方。
A
B
C
b
c
几何语言:
在Rt△ABC中 (已知)
由勾股定理得:
∴a2+b2=c2(勾股定理)
勾股定理:
∟
注意:
1.运用前提:已知直角三角形和直角。
2.揭示了直角三角形三条边的关系;
3.运用中要注意直角与斜边的对应关系;
4.三边中最长的边就是斜边。
a
关于勾股定理
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。
弦c
股b
勾a
图1-1
勾
股
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” 。传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” 。在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
a
b
c
c2=a2 + b2
a2=c2 - b2
b2 =c2 -a2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方:
如果知道了直角三角形两边的长度,那么应用勾股定理可以求出第三边的长度
勾股定理的证明(一)
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 。人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
证明:
教材P141
b
a
c
勾股定理的证明(二)
a
b
c
a
b
c
a
b
c
最早是由1700多年前三国时期的数学家赵爽为《周髀算经》作注时给出的,他用面积法证明了勾股定理。
你能用面积法证明勾股定理吗?
弦
图
证明:
a
b
c
你能用两种方法表示这个小正方形(空白部分)的面积吗?
勾股定理的证明(三)
证明:
将上面弦图中的四个三角形
重新拼成右图形式。
3
例题讲解
例1:在Rt△ABC中,∠C=90°。
(1) 已知:a=3,b=4,求c;
(2) 已知:a=24,c=25,求b;
(3) 已知:c=13,b=5,求a;
a
b
c
C
B
解:(1)在Rt△ABC中:
设c的长为x,由勾股定理得:
82+ x2=172
即:x=????????????????????? 解得:x=15
∴ c=15
?
独立完成第2和3小题
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
y=0
应用知识回归生活
解:由题可得
答:这棵树折断前高9米。
1、求出下列直角三角形中未知边的长度。
6
x
25
24
8
X
试一试
2.判断题 ①△ABC的两边AB=5,AC=12,则BC=13 ( ) ②△ABC的a=6,b=8,则c=10 ( ) 3.填空题 在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____,斜边为上的高为______。
?
?
24
4.8
A
B
C
D
3
例题讲解
例2:如果一个直角三角形的两条边长分别是6厘米和8厘米,求第三边长。
解:当8为直角边时:
斜边长为:
当8为斜边长时:
另一条直角边为:
10
试一试:课本51页练习2题。
答:第三边的长是10或 。
例3:在直角△ABC中, ∠C=90°,a、b、c分别为∠A、∠B 、∠C的对边。
(1)若a=3, b=4,求c的长;(2)若a=5, c =12,求b的长
(3)若a:b=3:4,c=15,求a、b的长
3
例题讲解
1、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
?
A
试一试:
2.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解:在Rt△ABC中,由勾股定理得:
BC2=AB2-AC2
=2.52-2.42
=0.49
答:这时梯脚与墙的距离是0.7米。
试一试:
B
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
试一试:
例4 : 如图,将长为5.41米的梯子AC斜靠在墙上
,BC长为2.16米,求梯子上端A到墙的底端B的
距离AB。(精确到0.01米)
解:在Rt△ABC中:
BC=2.16 AC=5.41
由勾股定理得:
≈4.96(米)
3
例题讲解
答:梯子上端A到墙的底端B的
距离AB是4.96米。
3
例题讲解
例5:如图,为了求出湖两岸的A、B 两点之间的距离,一个观测者在点C 设桩,使⊿ABC 恰好为直角三角形。通过测量,得到 AC 长160米,BC 长128米。问从点A穿过湖到点 B 有多远?
解:在Rt△ABC中:
AC=160米 BC=128米
= 96(米)
答:从点A穿过湖到点B有96米。
由勾股定理得:
3
例题讲解
3
例题讲解
A
D
B
C
3
4
例6.已知∠ACB=90°,
CD⊥AB,AC=3,BC=4。
求CD的长。
∟
解:∵∠ACB=90°
∵∠ACB=90°,CD⊥AB,
注意:在直角三角形中两直角边的积等于斜边与其高的积。
例7:如图正三角形ABC的边长为6。
(1)求高AD的长;(2)求三角形ABC的面积。
A
B
C
D
∟
提示:过点A作AD垂直BC于D
勾股小常识:勾股数
1、 a?+b? =c?,满足(a,b,c)=1则a,b,c,为基本勾股数如:3、4、5;5、12、 13;7、24、25……;
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、18……;
3、若a,b,c是一组基本的勾股数,则a,b,c不能同时为奇数或同时为偶数;
4、一组勾股数中必有一个数是5的倍数;
5、2mn,m?-n?,m?+n?为勾股数组,m>n﹥0,m,n一奇一偶;
a
3
6
9
—
3n
b
4
8
16
—
4n
c
5
15
20
—
5n
10
12
12
勾股定理
如果直角三角形两直角边长分别为a、b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
4
课堂小结
同学们,
辛苦了,
欢迎领导同仁莅临指导
老
大
师
大
导
大
领
大
好
大
欢迎指导
