14.1.2 直角三角形的判定4-6
文档属性
| 名称 | 14.1.2 直角三角形的判定4-6 |  | |
| 格式 | ppt | ||
| 文件大小 | 817.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 17:57:24 | ||
图片预览








文档简介
(共23张PPT)
14.1.2直角三角形的判定
第二课时
复习与巩固
a2 + b2 = c2
直角三角形的两条直角边的平方和等于它斜边的平方。
如果直角三角形两直角边分别为a,b,斜边为c,那么
勾股定理
直角三角形的哪些性质?
角:有一个角是直角,两锐角互余
边:两直角边的平方和等于斜边的平方
如何判定一个三角形是直角三角形
角:1.定义判定(有一个角是直角的三角形是直角三角形);
2.有两个内角互余的三角形是直角三角形
边:?
古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。这时构成了一个三角形,其中有一个角是直角 。
三角形的三边有什么关系呢?
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你能猜想出其中
的数学道理吗?
32 + 42 = 52
直角三角形
12
5
13
8
6
10
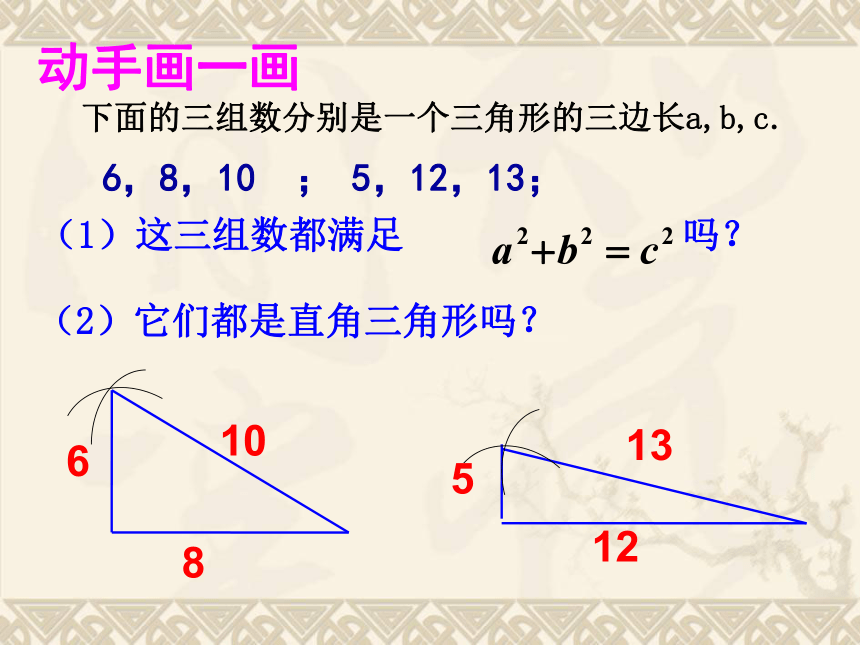
下面的三组数分别是一个三角形的三边长a,b,c.
6,8,10 ; 5,12,13;
(1)这三组数都满足
吗?
(2)它们都是直角三角形吗?
动手画一画
注意:
1.该定理叫做勾股定理的逆定理。用于从边上判断三角 形是不是直角三角形;
2.勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
3.最长边的对角为直角。
直角三角形的判定
归纳:
三角形的三边a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形 且c为直角边。
书写表述:
∵a2+b2=c2(已知)
∴ △ABC是Rt△且∠C=90°(勾股定理逆定理)
三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形 且c为直角边。
a2 - b2 = c2
直角三角形(a为斜边)
强调:
(1)勾股定理的逆定理主要用作从边去判断一个三角形是否是直角三角形.
(2)运用采用两条较短边的平方和与最长边的平方进行比较:若相等就是,不相等就不是。
(3)在运用中要分清最长边与直角的对应关系。
(4)一个三角形若有两条边的平方差等于第三边的平方,该三角形也为直角三角形。
b2 - c2 = a2
直角三角形(b为斜边)
例1:判断由线段a,b,c组成的三角形是不是直角三角形 如果是,请指明哪一边所对的角是直角。
(1) a=7,b=25,c=24; (2) a=13,b=11,c=9
解:(1)最长边为25
∵a2+c2=72+242
=49+576 =625
b2=252 =625
∴a2+c2=b2
∴以7, 25, 24为边长的三角形是直角三角形.边25所对的角是直角。
解:(2)最长边为13
∵b2+c2=112+92
=121+81 =202
a2=132 =169
∴b2+c2≠a2
∴以13, 11, 9为边长的三角形不是直角三角形.
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1)a=25,b=20,c=15____ _____ ;
(2)a=13,b=14,c=15____ _____ ;
(4) a=3,b=4,c=5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
课堂随练
解:如图,设每两个结的 距离为a(a>0),则AC=3a,BC=4a,AB=5a.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
例2. 据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.请说明为什么?
A
B
C
(1)三条线段a ,b ,c 满足 ,则这三条线段组成的三角形是直角三角形吗?斜边是哪个?
议一议
(2)如果一个三角形中较短两条边的平方和不等于最长边的平方,则这个三角形可能是直角三角形吗?
(3) 三角形三边比为a:b: c=3:4:5 ;这个三角形是直角三角形吗?
解:设a=3x,b=4x,c=5x
是,a为斜边。
不是
1. 满足下列条件△ABC, 不是直角三角形的是 ( )
A.a=1、b=2、c= B.a:b:c=3:4:5
C.∠C=∠B - ∠A D.∠A:∠B :∠C =3:4:5
2.判断下列是否构成直角三角形?若是指出斜边。
(3) a=15 b=20 c=25
(1) a=1 b=2 c=
3
(2) a=13 b=14 c=15
(4) a:b: c=13:12:5
是,b为斜边。
不是。
是,c为斜边。
是,a为斜边。
归纳:1.识别直角三角形有两种:一种利用角(有一个为直角),另一种利用边(勾股定理);2.已知三边成比例关系时,可以把份数直接当成边长来计算。
D
思考1:△ABC三边a,b,c为边向外作正方形,若S1+S2=S3成立,则△ABC是什么三角形?为什么?
A
B
C
a
b
c
S1
S2
S3
a
c
b
思考2:已知△ABC是直角三角形,以a,b,c为边向外作正方形,有S1+S2=S3?为什么?
a2 + b2 = c2
直角三角形
直角三角形
a2 + b2 = c2
结论:
1.直角三角形与三边平方的等量关系互逆;
2.以直角三角形三边作三个正方形,两个小正方形面积和等于大正方形面积;
3.如果两个正方形面积和等于第三个正方形的面积,那么用三个正方形的边长所围成的三角形为直角三角形。
作业:
1. △ABC中AB=8,AC=6,BC=10,则BC边上的高______.
2. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
3.在下列长度的各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13
4.如果线段a,b,c的比如下 ,则能组成直角三角形的是( )
A.1:2:4 B.1:3:5 C.3:4:7 D.5:12:13
5.判断由线段a,b,c组成的三角形是不是直角三角形 如果是,请指明哪一边所对的角是直角。
6.图,AD⊥CD ,AC⊥BC,AB=13, CD=3,AD=4.求:(1)求AC长;
(2)求BC长
B
A
D
C
12
13
3
4
例1. 一个零件的形状如左图所示,已知∠A=90°,按规定这个零件中∠DBC都应该为直角。工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
解:
在Rt△ABC中,AC=3cm,AB=4cm
由勾股定理得:
∴△BCD是直角三角形, CD所对的角是直角, 即∠DBC=90°
所以,这个零件符合要求。
例 2.在△ABC中,a=15, b=17, c=8,求此三角形的面积。
∴△ABC为直角三角形,∠B=90°
练习:在△ABC中,a=15, b=25, c=10,求此三角形b 边上的高。
∴ △ABC的面积为
例3.如图, AC⊥BC,AB=13,BC=12,CD=3 ,AD=4 。求:(1)求AC长, (2)求 的面积。
B
A
D
C
12
13
3
4
解: (1) ∵AC⊥BC,AB=13, BC=12
(2) ∵AC=5,AD=4,CD=3
∴42 + 32 = 25
52 = 25
∴AD2 + DC2 = AC2
∴三角形ADC为直角三角形,且∠D为直角。
∴S⊿ADC=3×4÷2=6。
B
A
D
C
13
3
4
B
A
D
C
12
13
3
4
变式:如图,AD⊥CD , AC⊥BC,AB=13, CD=3,AD=4.求:(1)求AC长;(2)求BC长
变式:如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长;(2)∠ACB的度数。
例4.有一块田地的形状和尺寸如图所示, ,AB=4,BC=3,
CD=12,AD=13, ∠B=90°试求它的面积。
∟
∟
A
B
C
D
变:如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13, ∠B=90°,求四边形ABCD的面积
D
B
A
C
┐
提示:连接AC,得到Rt△ABC 和Rt△ADC
提示:连接AC,得到Rt△ABC 和 △ADC ,再说明△ADC为直角三角形。
例5.如果△ABC的三边分别为a、b、c且满足a2+b2+c2+50=6a+8b+10c,判定△ABC的形状.
∴△ABC是直角三角形.
解:∵a2+b2+c2+50=6a+8b+10c
∴a2+b2+c2-6a-8b-10c +50 =0
∴a2 -6a +9+b2 -8b +16+c2-10c +25 =0
∴(a - 3)2 +(b -4 )2 +(c -5 )2 =0
∴a = 3,b =4 ,c =5
∴a2 + b2 = c2
∵32 + 42 = 52
例6.已知:如图,四边形ABCD中,AB=20,BC=15,CD=7,
AD=24, ∠B=90°若∠A=60°,求∠C。
A
B
C
D
20
15
7
24
例7.已知:如图,AD为三角形ABC的高,AB=13,AC=15,
AD=12,⑴求BC的长,⑵ 求三角形ABC的面积。
∟
D
C
B
A
作 业
1.下列条件能说明是直角三角形的是 ( )
2.在△ABC中,a=15, b=20, c=25, 此三角形的面积( )。
4. △ABC的三边分别为a、b、c且满足a2+b2+c2+ 200=12a+16b+20c,判定△ABC的形状.
6.已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
5.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,求AC.
3. 等腰△ABC的底为26,腰为12.则△ABC的面积( ) .
14.1.2直角三角形的判定
第二课时
复习与巩固
a2 + b2 = c2
直角三角形的两条直角边的平方和等于它斜边的平方。
如果直角三角形两直角边分别为a,b,斜边为c,那么
勾股定理
直角三角形的哪些性质?
角:有一个角是直角,两锐角互余
边:两直角边的平方和等于斜边的平方
如何判定一个三角形是直角三角形
角:1.定义判定(有一个角是直角的三角形是直角三角形);
2.有两个内角互余的三角形是直角三角形
边:?
古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。这时构成了一个三角形,其中有一个角是直角 。
三角形的三边有什么关系呢?
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你能猜想出其中
的数学道理吗?
32 + 42 = 52
直角三角形
12
5
13
8
6
10
下面的三组数分别是一个三角形的三边长a,b,c.
6,8,10 ; 5,12,13;
(1)这三组数都满足
吗?
(2)它们都是直角三角形吗?
动手画一画
注意:
1.该定理叫做勾股定理的逆定理。用于从边上判断三角 形是不是直角三角形;
2.勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
3.最长边的对角为直角。
直角三角形的判定
归纳:
三角形的三边a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形 且c为直角边。
书写表述:
∵a2+b2=c2(已知)
∴ △ABC是Rt△且∠C=90°(勾股定理逆定理)
三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形 且c为直角边。
a2 - b2 = c2
直角三角形(a为斜边)
强调:
(1)勾股定理的逆定理主要用作从边去判断一个三角形是否是直角三角形.
(2)运用采用两条较短边的平方和与最长边的平方进行比较:若相等就是,不相等就不是。
(3)在运用中要分清最长边与直角的对应关系。
(4)一个三角形若有两条边的平方差等于第三边的平方,该三角形也为直角三角形。
b2 - c2 = a2
直角三角形(b为斜边)
例1:判断由线段a,b,c组成的三角形是不是直角三角形 如果是,请指明哪一边所对的角是直角。
(1) a=7,b=25,c=24; (2) a=13,b=11,c=9
解:(1)最长边为25
∵a2+c2=72+242
=49+576 =625
b2=252 =625
∴a2+c2=b2
∴以7, 25, 24为边长的三角形是直角三角形.边25所对的角是直角。
解:(2)最长边为13
∵b2+c2=112+92
=121+81 =202
a2=132 =169
∴b2+c2≠a2
∴以13, 11, 9为边长的三角形不是直角三角形.
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1)a=25,b=20,c=15____ _____ ;
(2)a=13,b=14,c=15____ _____ ;
(4) a=3,b=4,c=5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
课堂随练
解:如图,设每两个结的 距离为a(a>0),则AC=3a,BC=4a,AB=5a.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
例2. 据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.请说明为什么?
A
B
C
(1)三条线段a ,b ,c 满足 ,则这三条线段组成的三角形是直角三角形吗?斜边是哪个?
议一议
(2)如果一个三角形中较短两条边的平方和不等于最长边的平方,则这个三角形可能是直角三角形吗?
(3) 三角形三边比为a:b: c=3:4:5 ;这个三角形是直角三角形吗?
解:设a=3x,b=4x,c=5x
是,a为斜边。
不是
1. 满足下列条件△ABC, 不是直角三角形的是 ( )
A.a=1、b=2、c= B.a:b:c=3:4:5
C.∠C=∠B - ∠A D.∠A:∠B :∠C =3:4:5
2.判断下列是否构成直角三角形?若是指出斜边。
(3) a=15 b=20 c=25
(1) a=1 b=2 c=
3
(2) a=13 b=14 c=15
(4) a:b: c=13:12:5
是,b为斜边。
不是。
是,c为斜边。
是,a为斜边。
归纳:1.识别直角三角形有两种:一种利用角(有一个为直角),另一种利用边(勾股定理);2.已知三边成比例关系时,可以把份数直接当成边长来计算。
D
思考1:△ABC三边a,b,c为边向外作正方形,若S1+S2=S3成立,则△ABC是什么三角形?为什么?
A
B
C
a
b
c
S1
S2
S3
a
c
b
思考2:已知△ABC是直角三角形,以a,b,c为边向外作正方形,有S1+S2=S3?为什么?
a2 + b2 = c2
直角三角形
直角三角形
a2 + b2 = c2
结论:
1.直角三角形与三边平方的等量关系互逆;
2.以直角三角形三边作三个正方形,两个小正方形面积和等于大正方形面积;
3.如果两个正方形面积和等于第三个正方形的面积,那么用三个正方形的边长所围成的三角形为直角三角形。
作业:
1. △ABC中AB=8,AC=6,BC=10,则BC边上的高______.
2. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
3.在下列长度的各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13
4.如果线段a,b,c的比如下 ,则能组成直角三角形的是( )
A.1:2:4 B.1:3:5 C.3:4:7 D.5:12:13
5.判断由线段a,b,c组成的三角形是不是直角三角形 如果是,请指明哪一边所对的角是直角。
6.图,AD⊥CD ,AC⊥BC,AB=13, CD=3,AD=4.求:(1)求AC长;
(2)求BC长
B
A
D
C
12
13
3
4
例1. 一个零件的形状如左图所示,已知∠A=90°,按规定这个零件中∠DBC都应该为直角。工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
解:
在Rt△ABC中,AC=3cm,AB=4cm
由勾股定理得:
∴△BCD是直角三角形, CD所对的角是直角, 即∠DBC=90°
所以,这个零件符合要求。
例 2.在△ABC中,a=15, b=17, c=8,求此三角形的面积。
∴△ABC为直角三角形,∠B=90°
练习:在△ABC中,a=15, b=25, c=10,求此三角形b 边上的高。
∴ △ABC的面积为
例3.如图, AC⊥BC,AB=13,BC=12,CD=3 ,AD=4 。求:(1)求AC长, (2)求 的面积。
B
A
D
C
12
13
3
4
解: (1) ∵AC⊥BC,AB=13, BC=12
(2) ∵AC=5,AD=4,CD=3
∴42 + 32 = 25
52 = 25
∴AD2 + DC2 = AC2
∴三角形ADC为直角三角形,且∠D为直角。
∴S⊿ADC=3×4÷2=6。
B
A
D
C
13
3
4
B
A
D
C
12
13
3
4
变式:如图,AD⊥CD , AC⊥BC,AB=13, CD=3,AD=4.求:(1)求AC长;(2)求BC长
变式:如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长;(2)∠ACB的度数。
例4.有一块田地的形状和尺寸如图所示, ,AB=4,BC=3,
CD=12,AD=13, ∠B=90°试求它的面积。
∟
∟
A
B
C
D
变:如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13, ∠B=90°,求四边形ABCD的面积
D
B
A
C
┐
提示:连接AC,得到Rt△ABC 和Rt△ADC
提示:连接AC,得到Rt△ABC 和 △ADC ,再说明△ADC为直角三角形。
例5.如果△ABC的三边分别为a、b、c且满足a2+b2+c2+50=6a+8b+10c,判定△ABC的形状.
∴△ABC是直角三角形.
解:∵a2+b2+c2+50=6a+8b+10c
∴a2+b2+c2-6a-8b-10c +50 =0
∴a2 -6a +9+b2 -8b +16+c2-10c +25 =0
∴(a - 3)2 +(b -4 )2 +(c -5 )2 =0
∴a = 3,b =4 ,c =5
∴a2 + b2 = c2
∵32 + 42 = 52
例6.已知:如图,四边形ABCD中,AB=20,BC=15,CD=7,
AD=24, ∠B=90°若∠A=60°,求∠C。
A
B
C
D
20
15
7
24
例7.已知:如图,AD为三角形ABC的高,AB=13,AC=15,
AD=12,⑴求BC的长,⑵ 求三角形ABC的面积。
∟
D
C
B
A
作 业
1.下列条件能说明是直角三角形的是 ( )
2.在△ABC中,a=15, b=20, c=25, 此三角形的面积( )。
4. △ABC的三边分别为a、b、c且满足a2+b2+c2+ 200=12a+16b+20c,判定△ABC的形状.
6.已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
5.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,求AC.
3. 等腰△ABC的底为26,腰为12.则△ABC的面积( ) .
