14.2勾股定理的应用7-9
图片预览





文档简介
(共26张PPT)
14.2勾股定理的
应用
第一课时
A
B
C
勾a
股b
弦c
一. 勾股定理:
直角三角形的两条直角边的
平方和等于它斜边的平方。
那么a2 + b2 = c2
如果在Rt ABC中,∠C=90°
语言叙述:
字母表示:
如果三角形的三边长a,b,c满足
那么这个三角形是直角三角形。
二.直角三角形的判定
复习
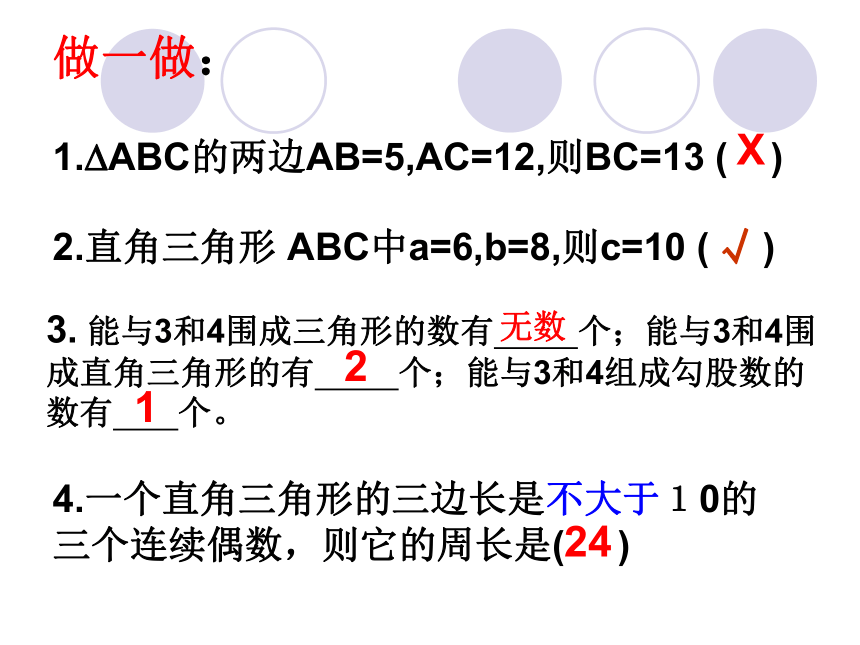
做一做:
1. ABC的两边AB=5,AC=12,则BC=13 ( )
2.直角三角形 ABC中a=6,b=8,则c=10 ( )
3. 能与3和4围成三角形的数有 个;能与3和4围成直角三角形的有 个;能与3和4组成勾股数的数有 个。
4.一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是( )
X
√
1
24
2
无数
A
B
例1.一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
C
D
一.最短路程问题
B
C
A
D
解:如图,由题意得:
在直角三角形ABC中,
CD=4,AD=20÷2=10,
根据勾股定理得:
答:最短路程为10.77厘米。
o
变式:一只蚂蚁从点A出发,沿着圆柱的侧面爬行到CD的中点O,已知底面周长为10,试求出爬行的最短路程。
A
A
B
D
C
4
3
O
解:如图,由题意得:
在直角三角形ABO中,OD=4÷2=2,AD=10 ÷2=5 , 根据勾股定理得:
答:最短路程为 厘米。
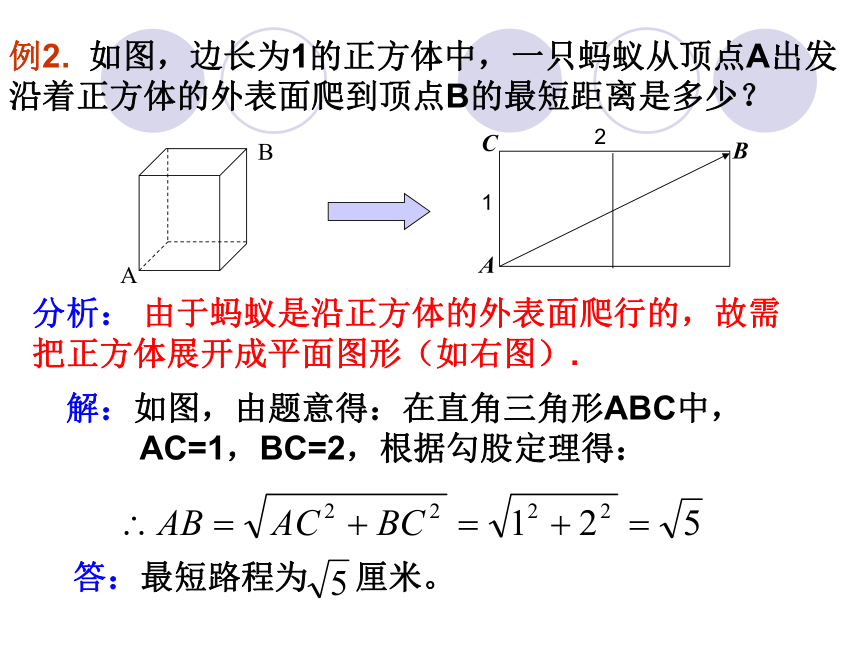
例2. 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是多少?
A
B
A
B
C
2
1
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如右图).
解:如图,由题意得:在直角三角形ABC中,
AC=1,BC=2,根据勾股定理得:
答:最短路程为 厘米。
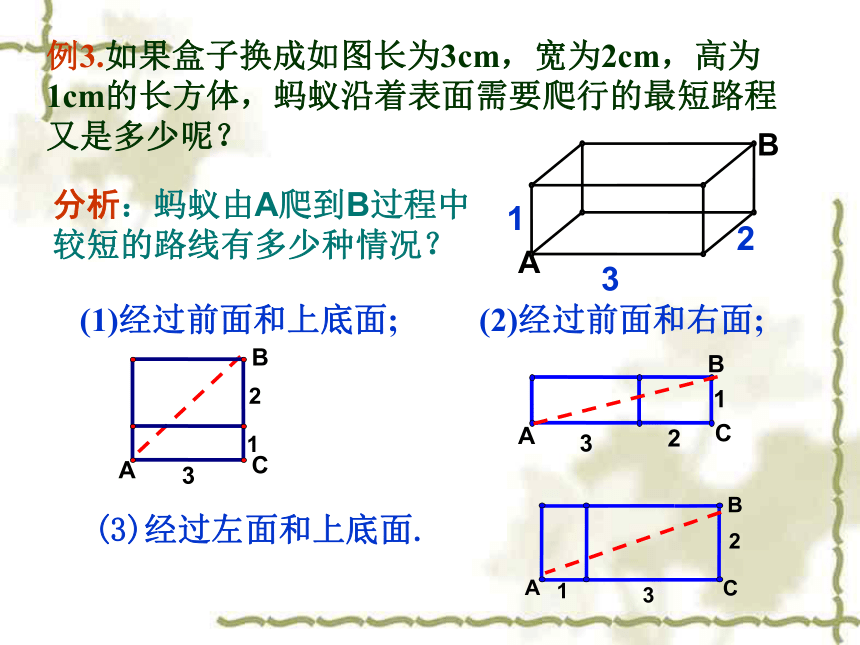
例3.如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
3
2
1
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
2
3
A
B
1
C
3
2
1
B
C
A
3
2
1
B
C
A
(1)当蚂蚁经过前面和上底面时,
解:
2
3
A
B
1
C
AB=
=
=
如图,最短路程为
(2)当蚂蚁经过前面和上右面时,
如图,最短路程为
3
2
1
B
C
A
AB=
=
=
(3)当蚂蚁经过左面和底面时,
如图,最短路程为
AB=
=
=
3
2
1
B
C
A
∴最短路程为 ㎝
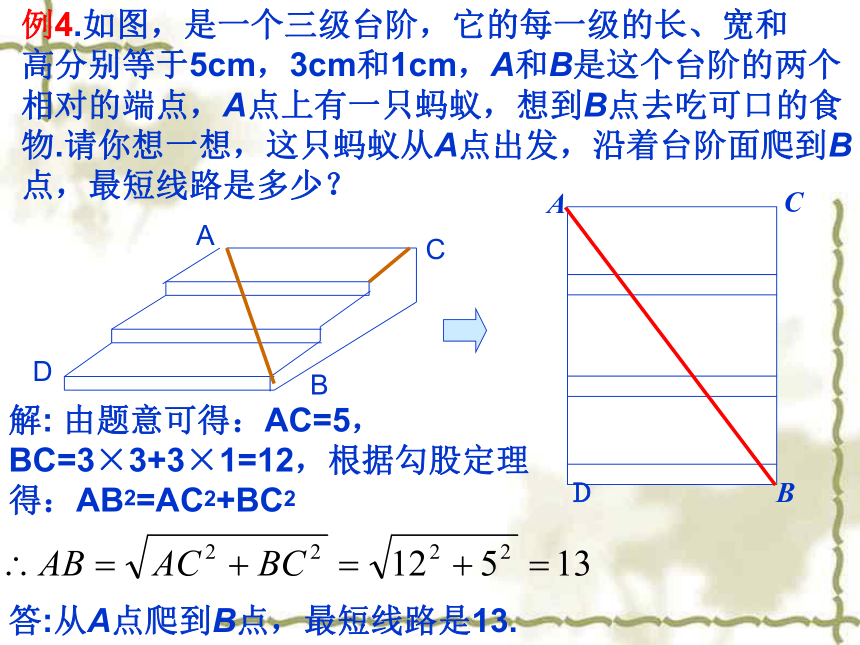
例4.如图,是一个三级台阶,它的每一级的长、宽和
高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食
物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B
点,最短线路是多少?
A
B
C
D
解: 由题意可得:AC=5, BC=3×3+3×1=12,根据勾股定理得:AB2=AC2+BC2
答:从A点爬到B点,最短线路是13.
A
B
C
D
小 结
1、立体图形中路线最短的问题,往往是把立体图形展开,得到平面图形.根据“两点之间,线段最短” 确定行走路线,根据勾股定理计算出最短距离.
2、在解决实际问题时,首先要画出适当的示意图,将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题.
应用勾股定理解决实际问题的一般思路:
2.有 一棵树直立在地上,树高20尺,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
20尺
3×7=21(尺)
1.小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?(1英寸=2.54厘米)
试一试:
1.三角形三边分别为6、8、10,那么最短边上的高为__.
2.一个三角形花坛的三边长分别为5cm,12cm,13cm,则这个花坛的面积是________.
3.直角三角形三边是连续整数,各边分别为___
4.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是___.
6.做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
作业
5.有 一棵树直立在地上,树高20米,粗3米,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?
14.2.1勾股定理的
应用
第二课时
例1.甲船以每小时30海里的速度,从A处向正北方向航行,同时乙船从A处以每小时40海里的速度向正西方向航行,两小时后,甲、乙两艘轮船相距多少海里?
A
B
C
解:如图,在Rt ABC中,∠A=90
BC2=AB2+AC2
BC= (30×2)2+(40×2)2
=100(海里)
答:甲乙两船相距100海里。
解:
CD=
CH=0.6+2.3=2.9>2.5
因此高度上有0.4米的余量,所以卡车能通过厂门.
=
=0.6米,
A
B
M
N
O
C
┏
D
H
2米
2.3米
如图,由题意得:OC=1米 (大门宽度一半), OD=0.8米 (卡车宽度一半)在Rt△OCD中,由勾股定理得
例2.一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
A
B
C
D
2米
2.3米
D
A
B
C
例3.有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
解:设,则水池的深度为X米,芦苇高为 (X+1)米. 根据题意得:
AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1 =12+1=13(米)
答:水池的深度为12米,芦苇高为13米.
例4.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8,BC=10,求: (1)CF (2)EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
解:由题意得,在RtΔABF中
AF=AD=BC=10,AB=DC=8
∴FC =4cm
设EC=x,则DE=EF=(8-x),
∵EF2=EC2+FC2
∴ (8-x)2 = x2+42
解得:x=3
四.折叠问题
1.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,求DE的长度?
A
B
C
D
E
F
(B)
(C)
2.如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
试一试
1.在运用勾股定理时,要看图形是不是直角三角形。
2.要学会根据题意画出草图,构建直角三角形。
3.考虑问题要全面,不要漏了某些情况。
1.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=_.
2.在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=__,面积为___,AB边上的高为____;
3.等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___
4.一根旗杆在离地面9米处断裂,旗杆顶部偏落在离旗杆底部12米处,问旗杆折断前有多高?
5. 校园操场边有两棵树,距离12米,一棵树高8米,另一棵树高13米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
6.在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
作业:
14.2.1勾股定理的
应用
第二课时
网格问题
A
B
C
例1.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC三边的大小关系?
F
E
D
解:如图,由题意得: ADC,
FBC , ABE为直角三角
形,根据勾股定理得:
∴AB>AC>BC
例2.如图,在5×5的正方形网格中,每个边长都为1,按下列要求画出图形。
(1).从点A出发画一条线段AB, 使它的另一个端点B在格点上,且长度为 ;
(2).画出以AB为边的等腰三角形,另一个顶点在格点上,且长度为无理数。
●
A
B
N
M
C
D
一种当AB为底,可作 ABC, ABD
二种当AB为腰,可作 ABN, ABM
因边长为无理数,所以 ABN, ABM不合题意。
解:根据题意可得:
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?
0
1
2
3
4
步骤:
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
例3:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
数学海螺图:
利用勾股定理作出长为
的线段.
1
1
14.2勾股定理的
应用
第一课时
A
B
C
勾a
股b
弦c
一. 勾股定理:
直角三角形的两条直角边的
平方和等于它斜边的平方。
那么a2 + b2 = c2
如果在Rt ABC中,∠C=90°
语言叙述:
字母表示:
如果三角形的三边长a,b,c满足
那么这个三角形是直角三角形。
二.直角三角形的判定
复习
做一做:
1. ABC的两边AB=5,AC=12,则BC=13 ( )
2.直角三角形 ABC中a=6,b=8,则c=10 ( )
3. 能与3和4围成三角形的数有 个;能与3和4围成直角三角形的有 个;能与3和4组成勾股数的数有 个。
4.一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是( )
X
√
1
24
2
无数
A
B
例1.一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
C
D
一.最短路程问题
B
C
A
D
解:如图,由题意得:
在直角三角形ABC中,
CD=4,AD=20÷2=10,
根据勾股定理得:
答:最短路程为10.77厘米。
o
变式:一只蚂蚁从点A出发,沿着圆柱的侧面爬行到CD的中点O,已知底面周长为10,试求出爬行的最短路程。
A
A
B
D
C
4
3
O
解:如图,由题意得:
在直角三角形ABO中,OD=4÷2=2,AD=10 ÷2=5 , 根据勾股定理得:
答:最短路程为 厘米。
例2. 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是多少?
A
B
A
B
C
2
1
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如右图).
解:如图,由题意得:在直角三角形ABC中,
AC=1,BC=2,根据勾股定理得:
答:最短路程为 厘米。
例3.如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
3
2
1
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
2
3
A
B
1
C
3
2
1
B
C
A
3
2
1
B
C
A
(1)当蚂蚁经过前面和上底面时,
解:
2
3
A
B
1
C
AB=
=
=
如图,最短路程为
(2)当蚂蚁经过前面和上右面时,
如图,最短路程为
3
2
1
B
C
A
AB=
=
=
(3)当蚂蚁经过左面和底面时,
如图,最短路程为
AB=
=
=
3
2
1
B
C
A
∴最短路程为 ㎝
例4.如图,是一个三级台阶,它的每一级的长、宽和
高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食
物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B
点,最短线路是多少?
A
B
C
D
解: 由题意可得:AC=5, BC=3×3+3×1=12,根据勾股定理得:AB2=AC2+BC2
答:从A点爬到B点,最短线路是13.
A
B
C
D
小 结
1、立体图形中路线最短的问题,往往是把立体图形展开,得到平面图形.根据“两点之间,线段最短” 确定行走路线,根据勾股定理计算出最短距离.
2、在解决实际问题时,首先要画出适当的示意图,将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题.
应用勾股定理解决实际问题的一般思路:
2.有 一棵树直立在地上,树高20尺,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
20尺
3×7=21(尺)
1.小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?(1英寸=2.54厘米)
试一试:
1.三角形三边分别为6、8、10,那么最短边上的高为__.
2.一个三角形花坛的三边长分别为5cm,12cm,13cm,则这个花坛的面积是________.
3.直角三角形三边是连续整数,各边分别为___
4.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是___.
6.做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
作业
5.有 一棵树直立在地上,树高20米,粗3米,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?
14.2.1勾股定理的
应用
第二课时
例1.甲船以每小时30海里的速度,从A处向正北方向航行,同时乙船从A处以每小时40海里的速度向正西方向航行,两小时后,甲、乙两艘轮船相距多少海里?
A
B
C
解:如图,在Rt ABC中,∠A=90
BC2=AB2+AC2
BC= (30×2)2+(40×2)2
=100(海里)
答:甲乙两船相距100海里。
解:
CD=
CH=0.6+2.3=2.9>2.5
因此高度上有0.4米的余量,所以卡车能通过厂门.
=
=0.6米,
A
B
M
N
O
C
┏
D
H
2米
2.3米
如图,由题意得:OC=1米 (大门宽度一半), OD=0.8米 (卡车宽度一半)在Rt△OCD中,由勾股定理得
例2.一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
A
B
C
D
2米
2.3米
D
A
B
C
例3.有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
解:设,则水池的深度为X米,芦苇高为 (X+1)米. 根据题意得:
AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1 =12+1=13(米)
答:水池的深度为12米,芦苇高为13米.
例4.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8,BC=10,求: (1)CF (2)EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
解:由题意得,在RtΔABF中
AF=AD=BC=10,AB=DC=8
∴FC =4cm
设EC=x,则DE=EF=(8-x),
∵EF2=EC2+FC2
∴ (8-x)2 = x2+42
解得:x=3
四.折叠问题
1.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,求DE的长度?
A
B
C
D
E
F
(B)
(C)
2.如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
试一试
1.在运用勾股定理时,要看图形是不是直角三角形。
2.要学会根据题意画出草图,构建直角三角形。
3.考虑问题要全面,不要漏了某些情况。
1.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=_.
2.在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=__,面积为___,AB边上的高为____;
3.等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___
4.一根旗杆在离地面9米处断裂,旗杆顶部偏落在离旗杆底部12米处,问旗杆折断前有多高?
5. 校园操场边有两棵树,距离12米,一棵树高8米,另一棵树高13米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
6.在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
作业:
14.2.1勾股定理的
应用
第二课时
网格问题
A
B
C
例1.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC三边的大小关系?
F
E
D
解:如图,由题意得: ADC,
FBC , ABE为直角三角
形,根据勾股定理得:
∴AB>AC>BC
例2.如图,在5×5的正方形网格中,每个边长都为1,按下列要求画出图形。
(1).从点A出发画一条线段AB, 使它的另一个端点B在格点上,且长度为 ;
(2).画出以AB为边的等腰三角形,另一个顶点在格点上,且长度为无理数。
●
A
B
N
M
C
D
一种当AB为底,可作 ABC, ABD
二种当AB为腰,可作 ABN, ABM
因边长为无理数,所以 ABN, ABM不合题意。
解:根据题意可得:
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?
0
1
2
3
4
步骤:
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
例3:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
数学海螺图:
利用勾股定理作出长为
的线段.
1
1
