第14章勾股定理全章复习课
图片预览










文档简介
(共30张PPT)
*
华东师大版《数学 · 八年级(上)》
第14章 勾股定理
复习课
教学目标:
1.熟记勾股定理及其逆定理
2.能综合应用勾股定理及其 逆定理解决问题.
设疑导学
1.自主复习课本108页———125页;
2.思考:你学到了哪些知识?
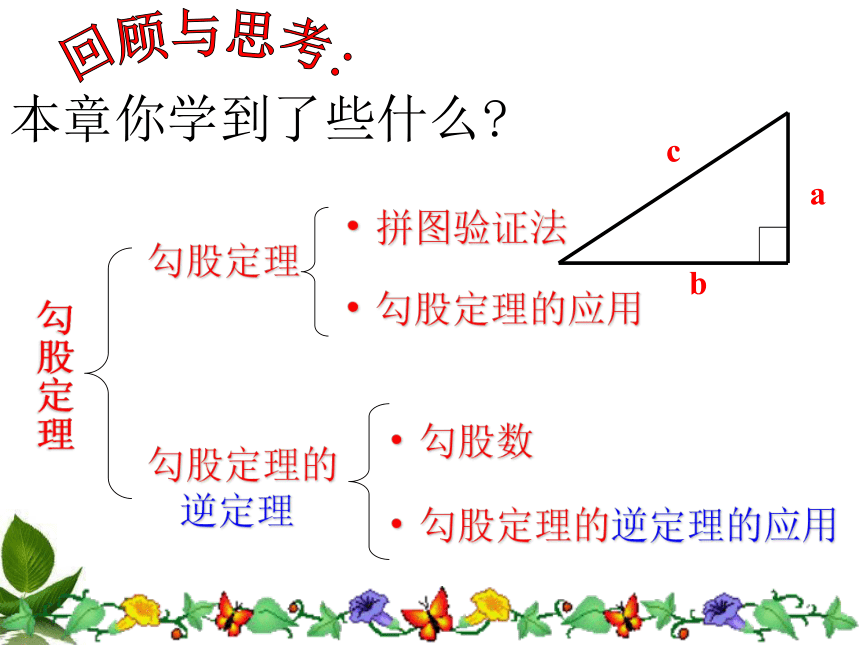
本章你学到了些什么
a
b
c
勾股定理
勾股定理
勾股定理的逆定理
拼图验证法
勾股定理的应用
勾股数
勾股定理的逆定理的应用
C
A
B
直角三角形有哪些特殊的性质
角
边
直角三角形的两锐角互余。
直角三角形两直角边的平方和等于
斜边的平方。
符号语言:
在Rt△ABC中∠C=90°
a2+b2=c2
a
b
c
∴
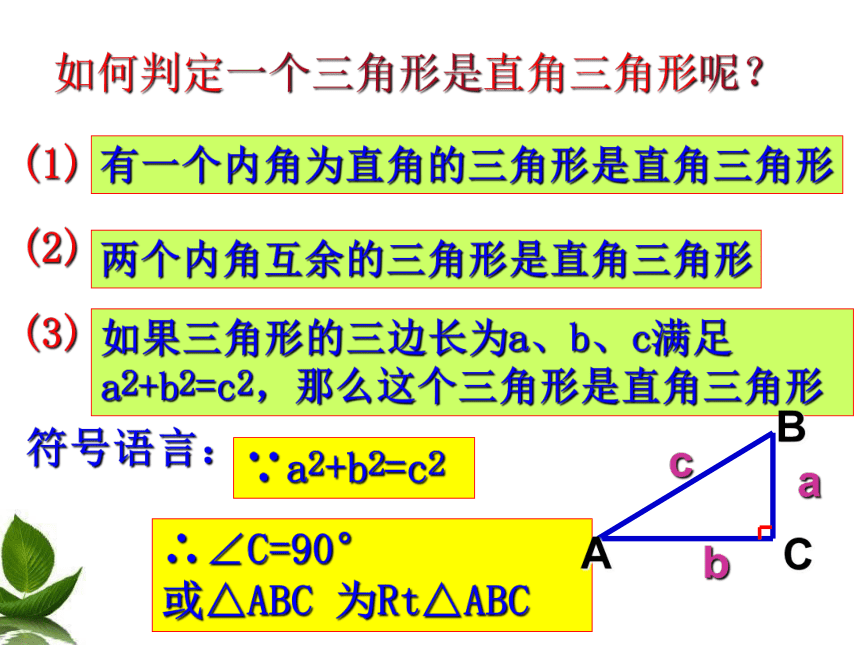
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
∴∠C=90°
或△ABC 为Rt△ABC
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
C
A
B
a
b
c
第1题
1.如图,字母A,B,C分别代表正方形的面积
(1)若B=225个单位面积,C=400个单位面积,
则A=______个单位面积.
(2)若A=225个单位面积,B=81个单位面
积,则C=______个单位面积.
2.已知直角三角形ABC中, (1)若AC=12,BC=9,则AB=______
(2)若AB=13,BC=5,则AC=_______
B
A
C
625
144
15
12
勾股数的妙用:你能速算吗
3.已知直角三角形中,c是斜边.
(1)a=3,b=4,c=_____
(2)a=6,b=____c=10
(3)a=____,b=40,c=50
(4)a=1.5,b=2,c=________
(5)a=8,b=15,c=________
(6)a=5,b=_______,c=13
(7)a=_____,b=40,c=41 (8)a=7,b=____c=25
你发现了什么
5
8
30
17
12
9
2.5
24
常见的勾股数:
3、4、5;
5、12、13;
6、8、10;
8、15、17;
9、40、41;
7、24、25.
记一记:(同桌互背)
4.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
45、60、75
C
5.下列不是一组勾股数的是( )
A、5、12、13 B、1.5、2、2.5
C、12、16、20 D、 7、24、25
B
6.若有两条线段分别为3,4,第三条线段为________时,才能组成一个直角三角形
5 或
问题一:如图,在矩形ABCD中,BC=8,CD=4,将矩形沿BD折叠,点A落在A′处,求重叠部分△BFD的面积。
A
B
C
D
F
A′
4
8
x
8-x
3
5
折叠出对称,勾股建方程!
问题二:已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2
C.48cm2 D.60cm2
C
A
B
a
b
c
A
1、如图,在直角三角形ABC中,∠C=90°,BC=3cm,AC=4cm,折叠∠CBA,使BC边落在AB边上,点C落在点E处,求CD的长。
B
C
A
D
E
测评反馈
2、如图,∠B=∠C=∠D=∠E=90°
且AB=CD=3,BC=4,DE=EF=2
求AF的长。
A
B
C
D
E
F
3
3
4
2
2
3
2
4
2
10
G
1.本节课你的收获?
2.解决本章的数学问题时,常用到哪些数学思想?
小结
如图,四边形ABCD中,∠B=∠ADC=90°,
∠C=45°,AD=1,BC=2, 求CD的长.
A
B
C
D
E
1
2
450
450
1
2
(1) ∠B=90°, ∠C=45°, BC=2
(2) ∠B=90°, ∠C=45°, 则∠E=45°
∵∠ADE=90°, ∠C=45°, AD=1
∴DE=AD=1
则BE=BC=2
拓展延伸:
探索是数学的生命线
再见
已知:如图,△ABC的周长24,
∠C=90°,且 b=6,则三角形的面积是多少
A
B
C
a
b
c
解:
∵周长是24,且b=6
∴a+c=24-6=18
设a=x,则c=18-x
∵ ∠C=90°,
∴a2+b2=c2
∴x2+62=(18-x)2
解得:x=8
合作探究
1、如图,在△ABC中,AB=AC=17,BC=16,(1)求△ABC的面积。
D
C
B
A
17
17
16
8
8
15
(2)求腰AC上的高。
如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
你发现什么规律了?
长宽高的平方和
的算术平方根
测评反馈
1.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 周长 = ____. =______ ,斜边上的高=______
2.一个直角三角形的面积54,且其中一条直角边
的长为9,则这个直角三角形的斜边长为_____
3.如上图,直角三角形的面积为24,AC=6,则它的周长为________
A
B
C
24
24
15
24
4.8
7.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
8.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。
B
A
D
C
13
3
4
B
A
D
C
12
13
3
4
勾股定理与逆定理的综合运用
9.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
B
A
D
C
12
13
3
4
勾股定理的应用四:构建直角三角形
1.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.
2.如图,小明和小方分别在C处同时出发,小明以每小时40千米的速度向南走,小方以每小时30千米的速度向西走,2小时后,小明在A处,小方在B处,请求出AB的距离.
5
4
3
2
1
6观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
再见
*
华东师大版《数学 · 八年级(上)》
第14章 勾股定理
复习课
教学目标:
1.熟记勾股定理及其逆定理
2.能综合应用勾股定理及其 逆定理解决问题.
设疑导学
1.自主复习课本108页———125页;
2.思考:你学到了哪些知识?
本章你学到了些什么
a
b
c
勾股定理
勾股定理
勾股定理的逆定理
拼图验证法
勾股定理的应用
勾股数
勾股定理的逆定理的应用
C
A
B
直角三角形有哪些特殊的性质
角
边
直角三角形的两锐角互余。
直角三角形两直角边的平方和等于
斜边的平方。
符号语言:
在Rt△ABC中∠C=90°
a2+b2=c2
a
b
c
∴
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
∴∠C=90°
或△ABC 为Rt△ABC
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
C
A
B
a
b
c
第1题
1.如图,字母A,B,C分别代表正方形的面积
(1)若B=225个单位面积,C=400个单位面积,
则A=______个单位面积.
(2)若A=225个单位面积,B=81个单位面
积,则C=______个单位面积.
2.已知直角三角形ABC中, (1)若AC=12,BC=9,则AB=______
(2)若AB=13,BC=5,则AC=_______
B
A
C
625
144
15
12
勾股数的妙用:你能速算吗
3.已知直角三角形中,c是斜边.
(1)a=3,b=4,c=_____
(2)a=6,b=____c=10
(3)a=____,b=40,c=50
(4)a=1.5,b=2,c=________
(5)a=8,b=15,c=________
(6)a=5,b=_______,c=13
(7)a=_____,b=40,c=41 (8)a=7,b=____c=25
你发现了什么
5
8
30
17
12
9
2.5
24
常见的勾股数:
3、4、5;
5、12、13;
6、8、10;
8、15、17;
9、40、41;
7、24、25.
记一记:(同桌互背)
4.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
45、60、75
C
5.下列不是一组勾股数的是( )
A、5、12、13 B、1.5、2、2.5
C、12、16、20 D、 7、24、25
B
6.若有两条线段分别为3,4,第三条线段为________时,才能组成一个直角三角形
5 或
问题一:如图,在矩形ABCD中,BC=8,CD=4,将矩形沿BD折叠,点A落在A′处,求重叠部分△BFD的面积。
A
B
C
D
F
A′
4
8
x
8-x
3
5
折叠出对称,勾股建方程!
问题二:已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2
C.48cm2 D.60cm2
C
A
B
a
b
c
A
1、如图,在直角三角形ABC中,∠C=90°,BC=3cm,AC=4cm,折叠∠CBA,使BC边落在AB边上,点C落在点E处,求CD的长。
B
C
A
D
E
测评反馈
2、如图,∠B=∠C=∠D=∠E=90°
且AB=CD=3,BC=4,DE=EF=2
求AF的长。
A
B
C
D
E
F
3
3
4
2
2
3
2
4
2
10
G
1.本节课你的收获?
2.解决本章的数学问题时,常用到哪些数学思想?
小结
如图,四边形ABCD中,∠B=∠ADC=90°,
∠C=45°,AD=1,BC=2, 求CD的长.
A
B
C
D
E
1
2
450
450
1
2
(1) ∠B=90°, ∠C=45°, BC=2
(2) ∠B=90°, ∠C=45°, 则∠E=45°
∵∠ADE=90°, ∠C=45°, AD=1
∴DE=AD=1
则BE=BC=2
拓展延伸:
探索是数学的生命线
再见
已知:如图,△ABC的周长24,
∠C=90°,且 b=6,则三角形的面积是多少
A
B
C
a
b
c
解:
∵周长是24,且b=6
∴a+c=24-6=18
设a=x,则c=18-x
∵ ∠C=90°,
∴a2+b2=c2
∴x2+62=(18-x)2
解得:x=8
合作探究
1、如图,在△ABC中,AB=AC=17,BC=16,(1)求△ABC的面积。
D
C
B
A
17
17
16
8
8
15
(2)求腰AC上的高。
如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
你发现什么规律了?
长宽高的平方和
的算术平方根
测评反馈
1.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 周长 = ____. =______ ,斜边上的高=______
2.一个直角三角形的面积54,且其中一条直角边
的长为9,则这个直角三角形的斜边长为_____
3.如上图,直角三角形的面积为24,AC=6,则它的周长为________
A
B
C
24
24
15
24
4.8
7.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
8.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。
B
A
D
C
13
3
4
B
A
D
C
12
13
3
4
勾股定理与逆定理的综合运用
9.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
B
A
D
C
12
13
3
4
勾股定理的应用四:构建直角三角形
1.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.
2.如图,小明和小方分别在C处同时出发,小明以每小时40千米的速度向南走,小方以每小时30千米的速度向西走,2小时后,小明在A处,小方在B处,请求出AB的距离.
5
4
3
2
1
6观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
再见
