山东省烟台市重点中学2023-2024学年高一上学期12月联考数学试题(含答案)
文档属性
| 名称 | 山东省烟台市重点中学2023-2024学年高一上学期12月联考数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 656.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 00:00:00 | ||
图片预览




文档简介
烟台市重点中学2023-2024学年高一上学期12月联考数学试题
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数的定义域为( )
A. B. C. D.
2.用二分法求方程的近似解时,可以取的一个区间是( )
A. B. C. D.
3.下列各式正确的是( )
A. B.
C. D.
4.若,,,则a,b,c的大小关系为( )
A. B. C. D.
5.若,则角的终边所在的象限是( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
6.已知角的顶点为坐标原点,始边为轴的正半轴,若角终边有一点,且,则( )
A.1 B.-1 C.±1 D.2
7.由于我国与以美国为首的西方国家在科技领域内的竞争日益激烈,美国加大了对我国一些高科技公司的打压,为突破西方的技术封锁和打压,我国的一些科技企业积极实施了独立自主、自力更生的策略,在一些领域取得了骄人的成绩.我国某科技公司为突破“芯片卡脖子”问题,实现芯片制造的国产化,加大了对相关产业的研发投入.若该公司2020年全年投入芯片制造方面的研发资金为120亿元,在此基础上,计划以后每年投入的研发资金比上一年增长9%,则该公司全年投入芯片制造方面的研发资金开始超过200亿元的年份是( )参考数据:,,.
A.2023年 B.2024年 C.2025年 D.2026年
8.已知函数,若,则实数的取值范围是( )
A. B.
C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分.
9.下列说法正确的是( )
A.钝角大于锐角
B.时间经过两个小时,时针转了60°
C.三角形的内角必是第一象限角或第二象限角
D.若是第三象限角,则是第二象限角或第四象限角
10.下列不等式中正确的是( )
A. B.
C. D.
11.下列命题正确的是( )
A.函数在区间上单调递减
B.函数在上单调递增
C.函数在区间上单调递减
D.函数与的图像关于直线对称
12.已知函数,若关于的方程有四个不同的实数解,它们从小到大依次记为,,,,则( )
A. B.
C. D.
三、填空题:本大题共4小题,每小题5分,共20分.
13.点是角终边上一点,则_________.
14.若,且,则实数的值为________.
15.方程的实数解为________.
16.若函数在区间上单调递增,则实数的取值范围是________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.求值:(1)
(2)
18.已知函数.
(1)求的定义域;
(2)判断的奇偶性并给予证明;
(3)求关于的不等式的解集.
19.如图,点A,B,C是圆O上的点.
(1)若,,求扇形的面积和弧的长;
(2)若扇形的面积为,求扇形周长的最小值,并求出此时的值.
20.已知函数(且)的图象过点.
(1)求a的值及的定义域;
(2)求在上的最大值;
(3)若,比较与的大小.
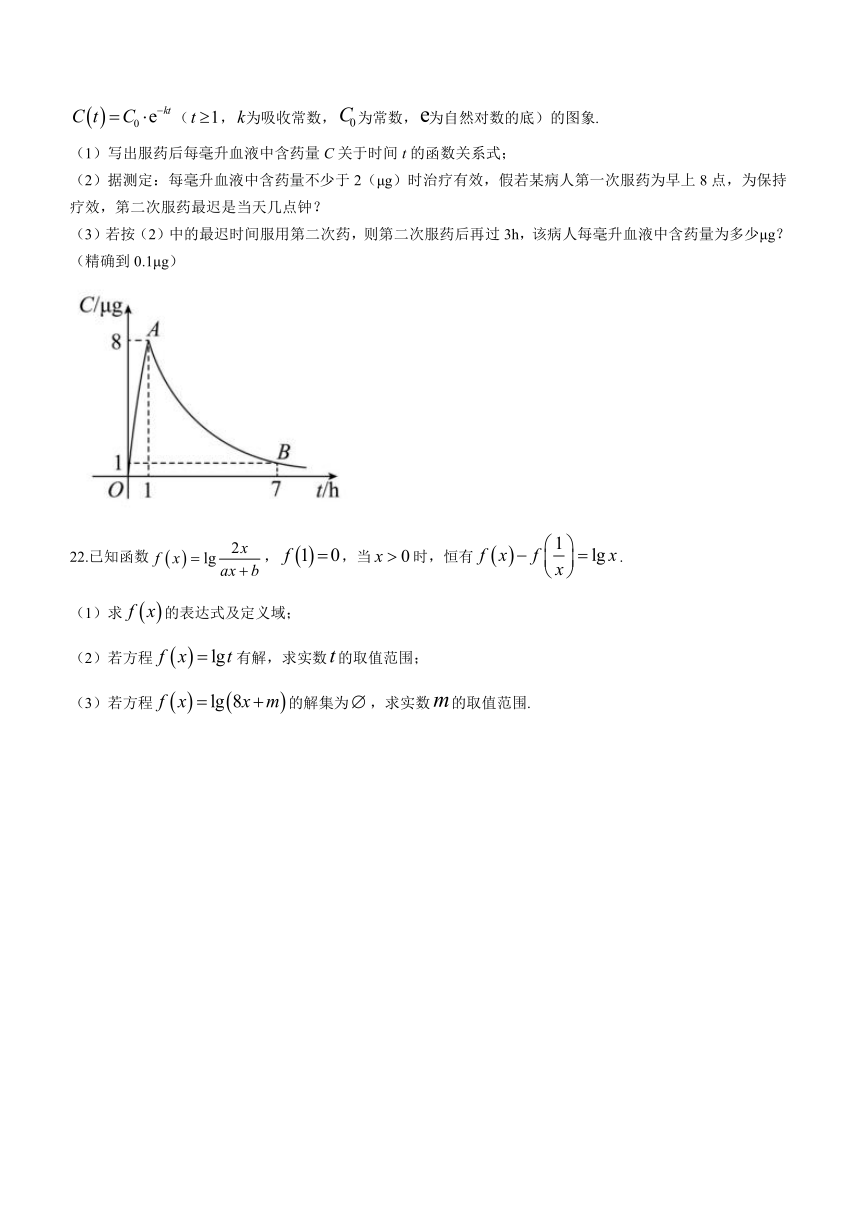
21.某医药研究所研发一种新药,据监测,如果成人按规定的剂量服用该药,服药1小时后血液中含药量达到峰值8μg,7小时后血液中含药量为1μg,服药后每毫升血液中的含药量与服药后的时间之间,近似满足如图所示的连续曲线,其中曲线段是函数的图象,曲线段是函数(,为吸收常数,为常数,为自然对数的底)的图象.
(1)写出服药后每毫升血液中含药量C关于时间t的函数关系式;
(2)据测定:每毫升血液中含药量不少于2(μg)时治疗有效,假若某病人第一次服药为早上8点,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过3h,该病人每毫升血液中含药量为多少μg?(精确到0.1μg)
22.已知函数,,当时,恒有.
(1)求的表达式及定义域;
(2)若方程有解,求实数的取值范围;
(3)若方程的解集为,求实数的取值范围.
答案
1.C 2.B 3.A 4.D
5.D【详解】因为,所以是第一象限角,
6.B【详解】由题意得,解得.
7.D【详解】设2020年后第年该公司全年投入芯片制造方面的研发资金开始超过200亿元,
由得,两边同取常用对数,得,所以,
所以从2026年开始,该公司全年投入芯片制造方面的研发资金开始超过200亿元.
8.D【详解】由可得:,则,所以函数是偶函数,则函数的图象关于直线对称,所以函数的图象关于直线对称,又时,在上单调递增,则在上单调递减,若,则,即,所以或,解得:或,所以实数的取值范围是.
9.AD
10.AC【详解】对于A,因为在上递增,且,所以,所以A正确,
对于B,因为在上递减,且,所以,所以B错误,
对于C,因为在上递减,且,所以,所以C正确,
对于D,因为,,所以,所以D错误,
11.BCD【详解】对于A,由,解得,或,故函数定义域为,由复合函数的单调性可知该函数的减区间为,故A错;
对于B,,由于在单调递增,且,所以在上单调递减,在上单调递增,因此在上单调递增,B正确;
对于C,当时,(即)在区间上单调递增,又因为为偶函数,其图象关于轴对称,所以在区间上单调递减,C正确;
对于D,由于函数与(即)互为反函数.所以两函数图象关于对称,D正确.
12.ACD【详解】当时,函数在上递减,函数值集合为,在上递增,函数值集合为,当时,函数在上递减,函数值集合为,在上递增,函数值集合为,作出函数的部分图象,如图,
方程有四个不同的实数解,等价于函数的图象与直线有4个公共点,
观察图象知,当时,函数的图象与直线有4个公共点,
即方程有四个不同的实数解,A正确;
因为二次函数图象对称轴为,因此,B不正确;
当时,,由,,得,因此,C正确;
当时,,由,得,解得,
且,则,有,所以,D正确.
13.【详解】根据任意角的三角函数定义,得
14.12【详解】由题设,,,所以,则.
15.【详解】由,得,所以,即,即,所以或(舍去),所以.
16.【详解】在区间上单调递增所以在区间上单调递增所以对称轴,解得.当时,,解得,的取值范围是.
17.(1)(2)
【分析】(1)根据指数的运算法则化简求值即可(2)根据对数的运算法则及性质化简求值.
【详解】(1)
.
(2)
18.(1);(2)函数为奇函数,证明见解析;(3)见解析.
【详解】(1)根据题意,函数,所以,解可得,所以函数的定义域为;
(2)由(1)得函数的定义域为,关于原点对称,因为函数,所以,所以函数为奇函数.
(3)根据题意,即,
当时,有,解可得,此时不等式的解集为;
当时,有,解可得,此时不等式的解集为.
所以当时,不等式的解集为;当时,不等式的解集为.
19.(1)面积为,弧的长为
(2),
【详解】(1)由题意知,设,所以根据扇形弧长;扇形面积;
(2)由,即,扇形的周长为当且仅当等号成立,所以由知:.
20.(1),定义域为;(2)最大值是.
【详解】(1)由已知,,,定义域为;
(2),
,,则,
所以,时取等号,最大值为;
22.(1)
(2)第二次服药最迟是当天下午13:00服药
(3)4.7μg
【详解】(1)当时,,把代入可得,
解得:,所以当时,,
当时,把、代入(k,a是常数),
得,解得,所以故.
(2)设第一次服药后最迟过t小时服第二次药,则,解得:,即第一次服药后5h后服第二次药,也即下午13:00服药;
(3)第二次服药3h后,每毫升血液中含第一次服药后的剩余量为:
每毫升血液中含第二次服药后剩余量为:
所以此时两次服药剩余的量为
故该病人每毫升血液中的含药量为4.7μg
23.(1),;(2);(3).
【详解】(1)∵当时,,,
即,即,.
整理得恒成立,∴,又,即,从而.
∴,
∵,∴,或,
∴的定义域为.
(2)方程有解,即,
∴,∴,∴,
∴,或,
解得或,
∴实数的取值范围.
(3)方程的解集为,
∴,∴,
∴,
方程的解集为,故有两种情况:
①方程无解,即,得,
②方程有解,
两根均在内,,
则
解得.
综合①②得实数的取值范围是.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数的定义域为( )
A. B. C. D.
2.用二分法求方程的近似解时,可以取的一个区间是( )
A. B. C. D.
3.下列各式正确的是( )
A. B.
C. D.
4.若,,,则a,b,c的大小关系为( )
A. B. C. D.
5.若,则角的终边所在的象限是( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
6.已知角的顶点为坐标原点,始边为轴的正半轴,若角终边有一点,且,则( )
A.1 B.-1 C.±1 D.2
7.由于我国与以美国为首的西方国家在科技领域内的竞争日益激烈,美国加大了对我国一些高科技公司的打压,为突破西方的技术封锁和打压,我国的一些科技企业积极实施了独立自主、自力更生的策略,在一些领域取得了骄人的成绩.我国某科技公司为突破“芯片卡脖子”问题,实现芯片制造的国产化,加大了对相关产业的研发投入.若该公司2020年全年投入芯片制造方面的研发资金为120亿元,在此基础上,计划以后每年投入的研发资金比上一年增长9%,则该公司全年投入芯片制造方面的研发资金开始超过200亿元的年份是( )参考数据:,,.
A.2023年 B.2024年 C.2025年 D.2026年
8.已知函数,若,则实数的取值范围是( )
A. B.
C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分.
9.下列说法正确的是( )
A.钝角大于锐角
B.时间经过两个小时,时针转了60°
C.三角形的内角必是第一象限角或第二象限角
D.若是第三象限角,则是第二象限角或第四象限角
10.下列不等式中正确的是( )
A. B.
C. D.
11.下列命题正确的是( )
A.函数在区间上单调递减
B.函数在上单调递增
C.函数在区间上单调递减
D.函数与的图像关于直线对称
12.已知函数,若关于的方程有四个不同的实数解,它们从小到大依次记为,,,,则( )
A. B.
C. D.
三、填空题:本大题共4小题,每小题5分,共20分.
13.点是角终边上一点,则_________.
14.若,且,则实数的值为________.
15.方程的实数解为________.
16.若函数在区间上单调递增,则实数的取值范围是________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.求值:(1)
(2)
18.已知函数.
(1)求的定义域;
(2)判断的奇偶性并给予证明;
(3)求关于的不等式的解集.
19.如图,点A,B,C是圆O上的点.
(1)若,,求扇形的面积和弧的长;
(2)若扇形的面积为,求扇形周长的最小值,并求出此时的值.
20.已知函数(且)的图象过点.
(1)求a的值及的定义域;
(2)求在上的最大值;
(3)若,比较与的大小.
21.某医药研究所研发一种新药,据监测,如果成人按规定的剂量服用该药,服药1小时后血液中含药量达到峰值8μg,7小时后血液中含药量为1μg,服药后每毫升血液中的含药量与服药后的时间之间,近似满足如图所示的连续曲线,其中曲线段是函数的图象,曲线段是函数(,为吸收常数,为常数,为自然对数的底)的图象.
(1)写出服药后每毫升血液中含药量C关于时间t的函数关系式;
(2)据测定:每毫升血液中含药量不少于2(μg)时治疗有效,假若某病人第一次服药为早上8点,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过3h,该病人每毫升血液中含药量为多少μg?(精确到0.1μg)
22.已知函数,,当时,恒有.
(1)求的表达式及定义域;
(2)若方程有解,求实数的取值范围;
(3)若方程的解集为,求实数的取值范围.
答案
1.C 2.B 3.A 4.D
5.D【详解】因为,所以是第一象限角,
6.B【详解】由题意得,解得.
7.D【详解】设2020年后第年该公司全年投入芯片制造方面的研发资金开始超过200亿元,
由得,两边同取常用对数,得,所以,
所以从2026年开始,该公司全年投入芯片制造方面的研发资金开始超过200亿元.
8.D【详解】由可得:,则,所以函数是偶函数,则函数的图象关于直线对称,所以函数的图象关于直线对称,又时,在上单调递增,则在上单调递减,若,则,即,所以或,解得:或,所以实数的取值范围是.
9.AD
10.AC【详解】对于A,因为在上递增,且,所以,所以A正确,
对于B,因为在上递减,且,所以,所以B错误,
对于C,因为在上递减,且,所以,所以C正确,
对于D,因为,,所以,所以D错误,
11.BCD【详解】对于A,由,解得,或,故函数定义域为,由复合函数的单调性可知该函数的减区间为,故A错;
对于B,,由于在单调递增,且,所以在上单调递减,在上单调递增,因此在上单调递增,B正确;
对于C,当时,(即)在区间上单调递增,又因为为偶函数,其图象关于轴对称,所以在区间上单调递减,C正确;
对于D,由于函数与(即)互为反函数.所以两函数图象关于对称,D正确.
12.ACD【详解】当时,函数在上递减,函数值集合为,在上递增,函数值集合为,当时,函数在上递减,函数值集合为,在上递增,函数值集合为,作出函数的部分图象,如图,
方程有四个不同的实数解,等价于函数的图象与直线有4个公共点,
观察图象知,当时,函数的图象与直线有4个公共点,
即方程有四个不同的实数解,A正确;
因为二次函数图象对称轴为,因此,B不正确;
当时,,由,,得,因此,C正确;
当时,,由,得,解得,
且,则,有,所以,D正确.
13.【详解】根据任意角的三角函数定义,得
14.12【详解】由题设,,,所以,则.
15.【详解】由,得,所以,即,即,所以或(舍去),所以.
16.【详解】在区间上单调递增所以在区间上单调递增所以对称轴,解得.当时,,解得,的取值范围是.
17.(1)(2)
【分析】(1)根据指数的运算法则化简求值即可(2)根据对数的运算法则及性质化简求值.
【详解】(1)
.
(2)
18.(1);(2)函数为奇函数,证明见解析;(3)见解析.
【详解】(1)根据题意,函数,所以,解可得,所以函数的定义域为;
(2)由(1)得函数的定义域为,关于原点对称,因为函数,所以,所以函数为奇函数.
(3)根据题意,即,
当时,有,解可得,此时不等式的解集为;
当时,有,解可得,此时不等式的解集为.
所以当时,不等式的解集为;当时,不等式的解集为.
19.(1)面积为,弧的长为
(2),
【详解】(1)由题意知,设,所以根据扇形弧长;扇形面积;
(2)由,即,扇形的周长为当且仅当等号成立,所以由知:.
20.(1),定义域为;(2)最大值是.
【详解】(1)由已知,,,定义域为;
(2),
,,则,
所以,时取等号,最大值为;
22.(1)
(2)第二次服药最迟是当天下午13:00服药
(3)4.7μg
【详解】(1)当时,,把代入可得,
解得:,所以当时,,
当时,把、代入(k,a是常数),
得,解得,所以故.
(2)设第一次服药后最迟过t小时服第二次药,则,解得:,即第一次服药后5h后服第二次药,也即下午13:00服药;
(3)第二次服药3h后,每毫升血液中含第一次服药后的剩余量为:
每毫升血液中含第二次服药后剩余量为:
所以此时两次服药剩余的量为
故该病人每毫升血液中的含药量为4.7μg
23.(1),;(2);(3).
【详解】(1)∵当时,,,
即,即,.
整理得恒成立,∴,又,即,从而.
∴,
∵,∴,或,
∴的定义域为.
(2)方程有解,即,
∴,∴,∴,
∴,或,
解得或,
∴实数的取值范围.
(3)方程的解集为,
∴,∴,
∴,
方程的解集为,故有两种情况:
①方程无解,即,得,
②方程有解,
两根均在内,,
则
解得.
综合①②得实数的取值范围是.
同课章节目录
