23.3.6相似三角形的应用 课件(共13张PPT)
文档属性
| 名称 | 23.3.6相似三角形的应用 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 591.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 12:43:10 | ||
图片预览




文档简介
(共13张PPT)
*
华东师大版《数学 · 九年级(上)》
§24.4.1 相似三角形的应用
一 课时
*
方法1:两角对应相等,两三角形相似
方法2:两边对应成比例且夹角相等,两三角形相似
方法3:三边对应成比例,两三角形相似
温故知新:
1、相似三角形的识别
2、相似三角形的性质?
1. 对应边成比例,对应角相等
2. 对应高、对应角平分 线、对应中线的比等于相似比
3. 周长比等于相似比
4. 面积比等于相似比的平方
*
埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.
给你一条1米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗
1米木杆
皮尺
平面镜
合作交流,思考探索
*
A
C
B
D
E
┐
┐
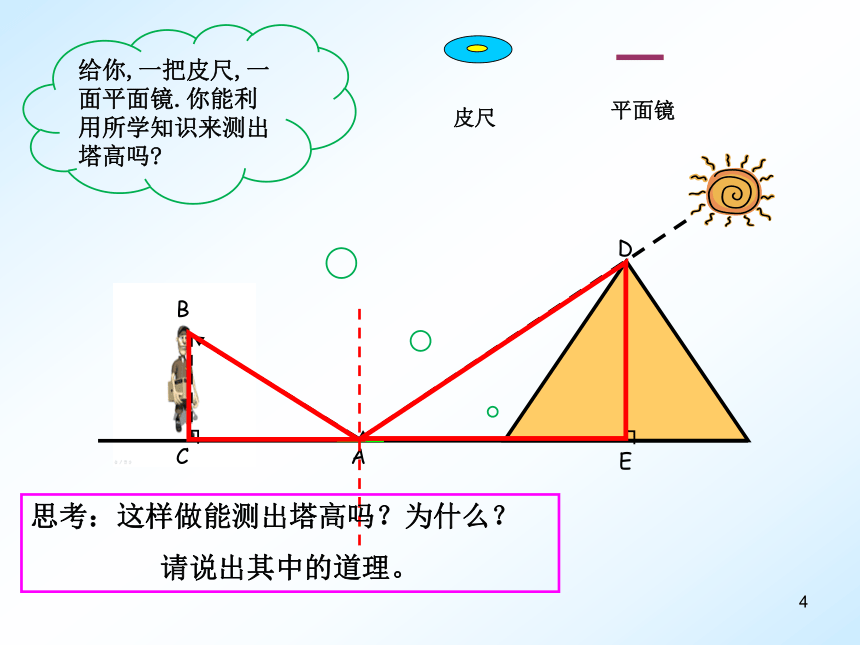
给你,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗
皮尺
平面镜
思考:这样做能测出塔高吗?为什么?
请说出其中的道理。
*
A
C
B
D
E
┐
┐
给你一条1米高的木杆,一把皮尺.你能利用所学知识来测出塔高吗
1米木杆
皮尺
思考:这样做能测出塔高吗?为什么?
请说出其中的道理。
*
例1:古代一位数学家想出了一种测量金字塔高度的方法:如图24.3.12所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.
A′
B
O
A
B′
O′
C
答:该金字塔高为137米.
解:
∵太阳光是平行光线,
∴ ∠OAB=∠O′A′B′.
又∵ ∠ABO=∠A′B′O′=90°.
∴ △OAB∽△O′A′B′,
∴ OB∶O′B′=AB∶A′B′,
*
在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?
解:设高楼的高度为X米,则
答:楼高36米.
3米
60米
*
C
B
D
2m
1m
E
例2:小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为2m,请帮助小丽求出旗杆的高度.
A
分析:由已知可得在太阳光下物体与其影长比值为=1:2.所以,AB:BE=1:2,若设AB=x,则BE=2x; 因两个三角形相似,,故有AB:DC=BE:EC; 因BC=20,DC=4,EC=20-2x,即求旗杆的高度AB.
解:
∴△ABE∽△DCE
∴AB:DC=BE:EC
由题意可得:
设AB=x,则BE=2x;
∠ABE=∠DCE=90度.
∠AEB=∠DEC
∵1m长的标杆影长为2m
∴AB:BE=1:2
∵BC=20,DC=4,
∴EC=2x-20
∴x:4=2x:(2x-20)
解得:x=14
答:旗杆高为14米.
*
A
B
D
C
E
F
练习:小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD= m,BC=10m,CD与地面成45°,求电线杆高度.
△ABF∽△DEF
由题意可得:
△DEC为等腰直角三角形
EC=DE=2,
BE=2+10=12,
∴AB:DC=BE:EC
设AB=x,则BF=2x;
∵1m长的标杆影长为2m
∴AB:BF=1:2
∵BE=12,DE=2,
∴EF=2x-12
∴x:2=2x:(2x-12)
解得:x=8
*
例3:如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
A
E
B
D
C
解: ∵∠ADB=∠EDC
∠ABC=∠ECD=90°
∴△ABD∽△ECD
答: 两岸间的大致距离为100米.
=100(米).
*
练习:如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。
O
分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。
解:
∵ OA:OC=OB:OD=n
且∠AOB=∠COD
∴△AOB∽△COD
∴ AB:CD=OA:OC=n
∵CD = b
∴x = (a-nb)/2
∴AB=CD·n = nb
*
课堂小结:
一 .相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
方法:通常用“在同一时刻物高与影长的比例”的原理解决;
2 测距(不能直接测量的两点间的距离)
方法:常构造相似三角形求解
二.解决实际问题时(如测高、测距)一般有以下步骤:
①审题 ②构建图形 ③利用相似解决问题
三.基本图形
⑴
⑵
⑶
⑷
*
课堂作业:
1.P63页练习1-2和64页6题。
2.P80页复习题7、15题。
*
华东师大版《数学 · 九年级(上)》
§24.4.1 相似三角形的应用
一 课时
*
方法1:两角对应相等,两三角形相似
方法2:两边对应成比例且夹角相等,两三角形相似
方法3:三边对应成比例,两三角形相似
温故知新:
1、相似三角形的识别
2、相似三角形的性质?
1. 对应边成比例,对应角相等
2. 对应高、对应角平分 线、对应中线的比等于相似比
3. 周长比等于相似比
4. 面积比等于相似比的平方
*
埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.
给你一条1米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗
1米木杆
皮尺
平面镜
合作交流,思考探索
*
A
C
B
D
E
┐
┐
给你,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗
皮尺
平面镜
思考:这样做能测出塔高吗?为什么?
请说出其中的道理。
*
A
C
B
D
E
┐
┐
给你一条1米高的木杆,一把皮尺.你能利用所学知识来测出塔高吗
1米木杆
皮尺
思考:这样做能测出塔高吗?为什么?
请说出其中的道理。
*
例1:古代一位数学家想出了一种测量金字塔高度的方法:如图24.3.12所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.
A′
B
O
A
B′
O′
C
答:该金字塔高为137米.
解:
∵太阳光是平行光线,
∴ ∠OAB=∠O′A′B′.
又∵ ∠ABO=∠A′B′O′=90°.
∴ △OAB∽△O′A′B′,
∴ OB∶O′B′=AB∶A′B′,
*
在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?
解:设高楼的高度为X米,则
答:楼高36米.
3米
60米
*
C
B
D
2m
1m
E
例2:小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为2m,请帮助小丽求出旗杆的高度.
A
分析:由已知可得在太阳光下物体与其影长比值为=1:2.所以,AB:BE=1:2,若设AB=x,则BE=2x; 因两个三角形相似,,故有AB:DC=BE:EC; 因BC=20,DC=4,EC=20-2x,即求旗杆的高度AB.
解:
∴△ABE∽△DCE
∴AB:DC=BE:EC
由题意可得:
设AB=x,则BE=2x;
∠ABE=∠DCE=90度.
∠AEB=∠DEC
∵1m长的标杆影长为2m
∴AB:BE=1:2
∵BC=20,DC=4,
∴EC=2x-20
∴x:4=2x:(2x-20)
解得:x=14
答:旗杆高为14米.
*
A
B
D
C
E
F
练习:小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD= m,BC=10m,CD与地面成45°,求电线杆高度.
△ABF∽△DEF
由题意可得:
△DEC为等腰直角三角形
EC=DE=2,
BE=2+10=12,
∴AB:DC=BE:EC
设AB=x,则BF=2x;
∵1m长的标杆影长为2m
∴AB:BF=1:2
∵BE=12,DE=2,
∴EF=2x-12
∴x:2=2x:(2x-12)
解得:x=8
*
例3:如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
A
E
B
D
C
解: ∵∠ADB=∠EDC
∠ABC=∠ECD=90°
∴△ABD∽△ECD
答: 两岸间的大致距离为100米.
=100(米).
*
练习:如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。
O
分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。
解:
∵ OA:OC=OB:OD=n
且∠AOB=∠COD
∴△AOB∽△COD
∴ AB:CD=OA:OC=n
∵CD = b
∴x = (a-nb)/2
∴AB=CD·n = nb
*
课堂小结:
一 .相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
方法:通常用“在同一时刻物高与影长的比例”的原理解决;
2 测距(不能直接测量的两点间的距离)
方法:常构造相似三角形求解
二.解决实际问题时(如测高、测距)一般有以下步骤:
①审题 ②构建图形 ③利用相似解决问题
三.基本图形
⑴
⑵
⑶
⑷
*
课堂作业:
1.P63页练习1-2和64页6题。
2.P80页复习题7、15题。
