23.4.1中位线复习 课件(共13张PPT)
文档属性
| 名称 | 23.4.1中位线复习 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 12:49:32 | ||
图片预览





文档简介
(共13张PPT)
*
华东师大版《数学 · 九年级(上)》
§24.4.3 中位线综合应用
第三课时
*
复习提问:
1三角形中位线定义和性质:
思考:
顺次连结对角线相等的四边形各边中点所得的四边形是什么?
顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
顺次连结对角线相等且垂直的四边形各边中点所得四边形是什么?
顺次连结对角线相等且垂直的四边形各边中点所得四边形是什么?
连接两腰中点的线段叫做梯形的中位线
性质:三角形的中位线平行于第三边,且等于第三边的一半;
推论:过三角形一边中点并平行于另一边的直线必平分第三边;
2梯形中位线定义和性质:
连接三角形两边中点的线段叫做三角形的中位线
性质:梯形的中位线平行于上下底,且等于上下底和的一半;
推论:梯形面积等于中位线与高的乘积;
*
梯形中位线的定义:
梯形中位线性质:
A
B
D
C
F
E
梯形的面积公式:
EF=1/2(AD+BC)
梯形两腰中点的连线叫做梯形的中位线
梯形的中位线平行于两底,
并且等于两底和的一半.
EF∥AD ∥BC
S= (AD+BC)h=EF×h
*
想一想:你会求BC的长吗?
P
A
E
B
C
D
F
20
试一试:
1.如图,三角架各横木之间互相平行,且PA=AE=BE, PD=DF=FC.若EF=40cm,则AD= cm.
2.铁匠师傅要把一块周长为30cm的等边三角形铁皮,裁成四块形状大小完全相同的小三角形铁皮, 你能帮助他想出办法吗?说说你的想法。你能知道每块小三角形铁皮的周长是____ CM
A
B
C
E
F
G
15
*
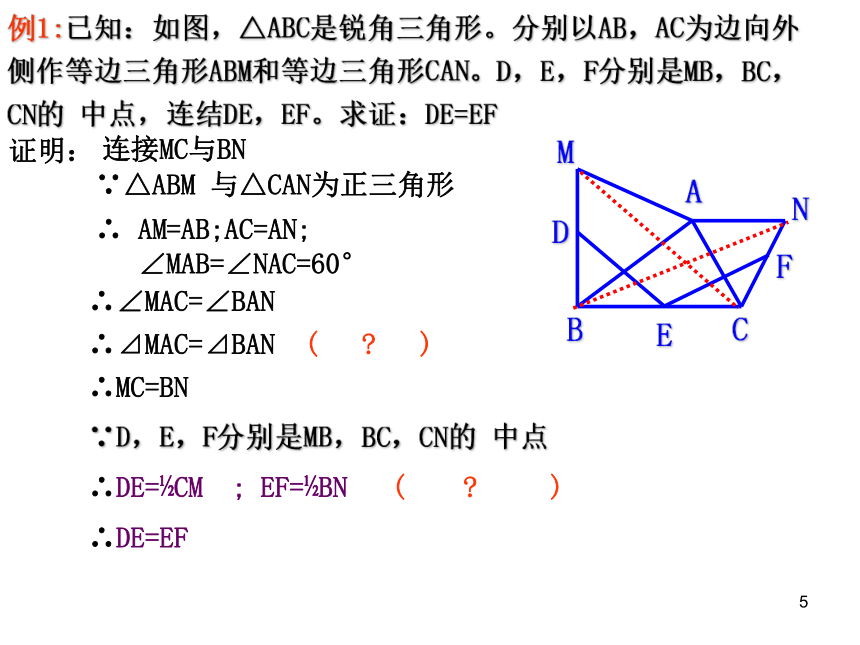
例1:已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的 中点,连结DE,EF。求证:DE=EF
A
B
C
D
E
F
N
M
证明:
∵△ABM 与△CAN为正三角形
连接MC与BN
∴ AM=AB;AC=AN;
∠MAB=∠NAC=60°
∴∠MAC=∠BAN
∴⊿MAC=⊿BAN ( )
∴MC=BN
∵D,E,F分别是MB,BC,CN的 中点
∴DE= CM ; EF= BN ( )
∴DE=EF
*
练习:已知:E为平行四边形ABCD中DC边的延长线上一点,
且CE=DC,连结AE,分别交BC、BD于点F、G,连接AC交BD
于O,连结OF.求证: AB=2FO
A
D
B
C
E
G
F
O
证明:
∵四边形ABCD为□
∴ DC=AB;DC∥AB;O为BD中点
∴∠BAF=∠E
∵CE=DC
∴ AB=EC
∵∠AFB=∠EFC
∴⊿MAC=⊿BAN ( )
∴ BF=FC
即:F为BC中点
∵O、F分别为AC、BC中点
即AB=2FO
∴FO= AB
*
例2: 如图,梯形ABCD中,AD//BC,AB=DC,中位线EF交BD于点M,EM=4,FM=10,AB=12,求梯形ABCD的周长和各角的度数。
解:
(1)∵EF是梯形的中位线
∴EM= AD;MF= BC ( )
即:AD=2EM; BC=2MF
∵EM=4,FM=10
∴AD=8; BC=20
∵AB=DC;AB=12
∴周长=8+20+12+12=52
N
(2)过点A作AN∥DC交BC于
∵AD//BC,AN∥DC
∴四边形ANCD为□
∴AN=AD=B; AN=DC=12
∴BN=BC-AD=20-8=12
∴AB=AN=BN=12
∴⊿ABN为正三角形
∴∠ABN=60°
∴∠C=60°, ∠BAD=∠ADC=120°
*
练一练:
1.梯形的上底长4cm,下底长6cm,则中位线长 cm.
2.梯形上底长6cm,中位线长8cm,则下底长 cm.
3.等腰梯形的中位线长6,腰长5, 梯形的周长是 cm.
4.若梯形的中位线长6cm,高为5cm, 求梯形的面积.
5.一个等腰梯形的周长为80cm,如果中位线长与腰长相等,高为12cm,求梯形的面积.
*
例3:如图,D,E,F,分别是△ABC各边的中点,AH是△ABC的高,四边形DHEF是等腰梯形吗?
A
B
C
H
F
D
E
∟
∵D,F是△ABC两边的中点
∴DF是△ABC的中位线
∴DF∥BC,即DF∥HE
∵DH、EF 不平行
∴四边形DHEF是梯形
∵ AH是△ABC的高,D是AB的中点
∴DH= AB ( )
∵E,F是AC,BC的中点
∴EF= AB ( )
∴DH=EF
∴四边形DHEF是等腰梯形
证明:
*
练习:四边形ABCD,AC,BD交与点O,且AC=BD,点E,F,K分别是AB,CD,AD的中点,连接EF交AC、BD于G、H.
求证:OG=OH
K
∵D,F,K是AB,DC,AD边的中点
证明:
分别连接E、F与AD中点K
∴EK∥BD, EK= BD
FK∥AC, FK= AC
∴∠1=∠3 ,∠2=∠4
1
2
3
4
∵AC=BD
∴EK=FK
∴∠3=∠4
∴∠1=∠2
∴OG=OH
*
E
方法1:AC=AO+OC,
AO= AD,OC= BC,
MN= (AD+BC)
方法2:过点D作DE ∥AC交BC延长于点E,MN=1/2(AD+BC)
例4:如图,在梯形ABCD中,AD∥BC,对角线AC与BD垂直相交于点O,MN是梯形ABCD的中位线,∠1=30°.
求证:AC=MN
*
练一练:
如图,梯形ABCD中,AD∥BC, E是腰AB的中点,且DE⊥CE. 求证: DC=AD+CB.
A
B
C
D
·
E
F
连接E与DC边中点F
EF= .(AD+BC)(梯形中位线)
EF= .DC(直角三角形斜边中线等于斜边一半)
*
梯形的中位线是16cm,它被一条对角线分成两部分差是4,求梯形的两底。
梯形上底长10,中位线长12,求下底及梯形被中位线分成的两部分的面积比。
等腰梯形两底差为4,中位线长为6,腰长为4,求等腰梯形的面积
作业:
4.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
(提示:连接AC与BD)
*
华东师大版《数学 · 九年级(上)》
§24.4.3 中位线综合应用
第三课时
*
复习提问:
1三角形中位线定义和性质:
思考:
顺次连结对角线相等的四边形各边中点所得的四边形是什么?
顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
顺次连结对角线相等且垂直的四边形各边中点所得四边形是什么?
顺次连结对角线相等且垂直的四边形各边中点所得四边形是什么?
连接两腰中点的线段叫做梯形的中位线
性质:三角形的中位线平行于第三边,且等于第三边的一半;
推论:过三角形一边中点并平行于另一边的直线必平分第三边;
2梯形中位线定义和性质:
连接三角形两边中点的线段叫做三角形的中位线
性质:梯形的中位线平行于上下底,且等于上下底和的一半;
推论:梯形面积等于中位线与高的乘积;
*
梯形中位线的定义:
梯形中位线性质:
A
B
D
C
F
E
梯形的面积公式:
EF=1/2(AD+BC)
梯形两腰中点的连线叫做梯形的中位线
梯形的中位线平行于两底,
并且等于两底和的一半.
EF∥AD ∥BC
S= (AD+BC)h=EF×h
*
想一想:你会求BC的长吗?
P
A
E
B
C
D
F
20
试一试:
1.如图,三角架各横木之间互相平行,且PA=AE=BE, PD=DF=FC.若EF=40cm,则AD= cm.
2.铁匠师傅要把一块周长为30cm的等边三角形铁皮,裁成四块形状大小完全相同的小三角形铁皮, 你能帮助他想出办法吗?说说你的想法。你能知道每块小三角形铁皮的周长是____ CM
A
B
C
E
F
G
15
*
例1:已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的 中点,连结DE,EF。求证:DE=EF
A
B
C
D
E
F
N
M
证明:
∵△ABM 与△CAN为正三角形
连接MC与BN
∴ AM=AB;AC=AN;
∠MAB=∠NAC=60°
∴∠MAC=∠BAN
∴⊿MAC=⊿BAN ( )
∴MC=BN
∵D,E,F分别是MB,BC,CN的 中点
∴DE= CM ; EF= BN ( )
∴DE=EF
*
练习:已知:E为平行四边形ABCD中DC边的延长线上一点,
且CE=DC,连结AE,分别交BC、BD于点F、G,连接AC交BD
于O,连结OF.求证: AB=2FO
A
D
B
C
E
G
F
O
证明:
∵四边形ABCD为□
∴ DC=AB;DC∥AB;O为BD中点
∴∠BAF=∠E
∵CE=DC
∴ AB=EC
∵∠AFB=∠EFC
∴⊿MAC=⊿BAN ( )
∴ BF=FC
即:F为BC中点
∵O、F分别为AC、BC中点
即AB=2FO
∴FO= AB
*
例2: 如图,梯形ABCD中,AD//BC,AB=DC,中位线EF交BD于点M,EM=4,FM=10,AB=12,求梯形ABCD的周长和各角的度数。
解:
(1)∵EF是梯形的中位线
∴EM= AD;MF= BC ( )
即:AD=2EM; BC=2MF
∵EM=4,FM=10
∴AD=8; BC=20
∵AB=DC;AB=12
∴周长=8+20+12+12=52
N
(2)过点A作AN∥DC交BC于
∵AD//BC,AN∥DC
∴四边形ANCD为□
∴AN=AD=B; AN=DC=12
∴BN=BC-AD=20-8=12
∴AB=AN=BN=12
∴⊿ABN为正三角形
∴∠ABN=60°
∴∠C=60°, ∠BAD=∠ADC=120°
*
练一练:
1.梯形的上底长4cm,下底长6cm,则中位线长 cm.
2.梯形上底长6cm,中位线长8cm,则下底长 cm.
3.等腰梯形的中位线长6,腰长5, 梯形的周长是 cm.
4.若梯形的中位线长6cm,高为5cm, 求梯形的面积.
5.一个等腰梯形的周长为80cm,如果中位线长与腰长相等,高为12cm,求梯形的面积.
*
例3:如图,D,E,F,分别是△ABC各边的中点,AH是△ABC的高,四边形DHEF是等腰梯形吗?
A
B
C
H
F
D
E
∟
∵D,F是△ABC两边的中点
∴DF是△ABC的中位线
∴DF∥BC,即DF∥HE
∵DH、EF 不平行
∴四边形DHEF是梯形
∵ AH是△ABC的高,D是AB的中点
∴DH= AB ( )
∵E,F是AC,BC的中点
∴EF= AB ( )
∴DH=EF
∴四边形DHEF是等腰梯形
证明:
*
练习:四边形ABCD,AC,BD交与点O,且AC=BD,点E,F,K分别是AB,CD,AD的中点,连接EF交AC、BD于G、H.
求证:OG=OH
K
∵D,F,K是AB,DC,AD边的中点
证明:
分别连接E、F与AD中点K
∴EK∥BD, EK= BD
FK∥AC, FK= AC
∴∠1=∠3 ,∠2=∠4
1
2
3
4
∵AC=BD
∴EK=FK
∴∠3=∠4
∴∠1=∠2
∴OG=OH
*
E
方法1:AC=AO+OC,
AO= AD,OC= BC,
MN= (AD+BC)
方法2:过点D作DE ∥AC交BC延长于点E,MN=1/2(AD+BC)
例4:如图,在梯形ABCD中,AD∥BC,对角线AC与BD垂直相交于点O,MN是梯形ABCD的中位线,∠1=30°.
求证:AC=MN
*
练一练:
如图,梯形ABCD中,AD∥BC, E是腰AB的中点,且DE⊥CE. 求证: DC=AD+CB.
A
B
C
D
·
E
F
连接E与DC边中点F
EF= .(AD+BC)(梯形中位线)
EF= .DC(直角三角形斜边中线等于斜边一半)
*
梯形的中位线是16cm,它被一条对角线分成两部分差是4,求梯形的两底。
梯形上底长10,中位线长12,求下底及梯形被中位线分成的两部分的面积比。
等腰梯形两底差为4,中位线长为6,腰长为4,求等腰梯形的面积
作业:
4.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
(提示:连接AC与BD)
