23.5 位似图形 课件(共17张PPT)
文档属性
| 名称 | 23.5 位似图形 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 12:51:18 | ||
图片预览



文档简介
(共17张PPT)
华东师大版《数学 · 九年级(上)》
§24.5 画位似图形
一课时
*
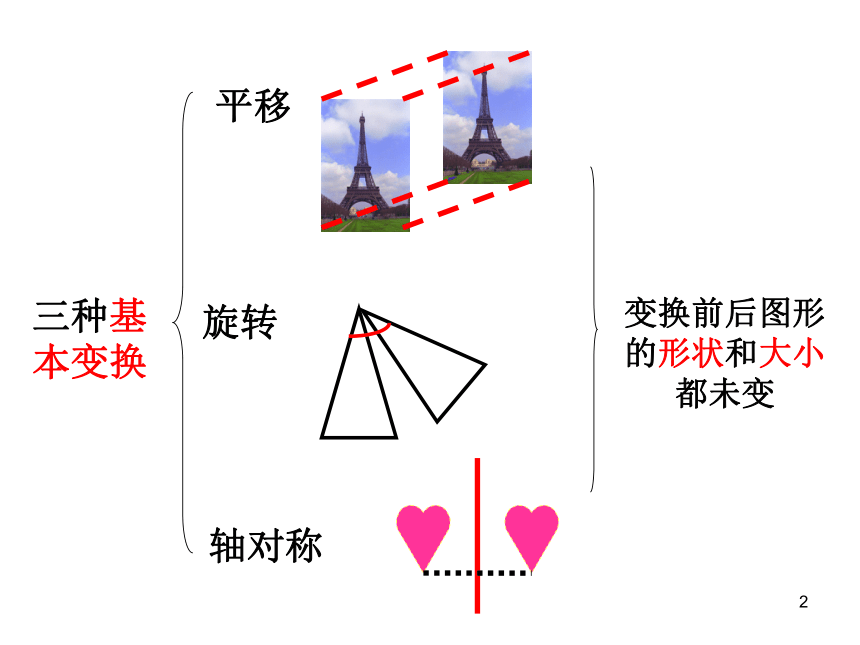
三种基本变换
平移
旋转
轴对称
变换前后图形的形状和大小都未变
*
相似与轴对称,平移,旋转一样,也是图形之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
思考:相似图形需要具备哪些条件
对应角都相等,对应边都成比例
如何便捷的画出一个图形的相似图形呢
这节课我们学习画相似图形的一种特殊方法
*
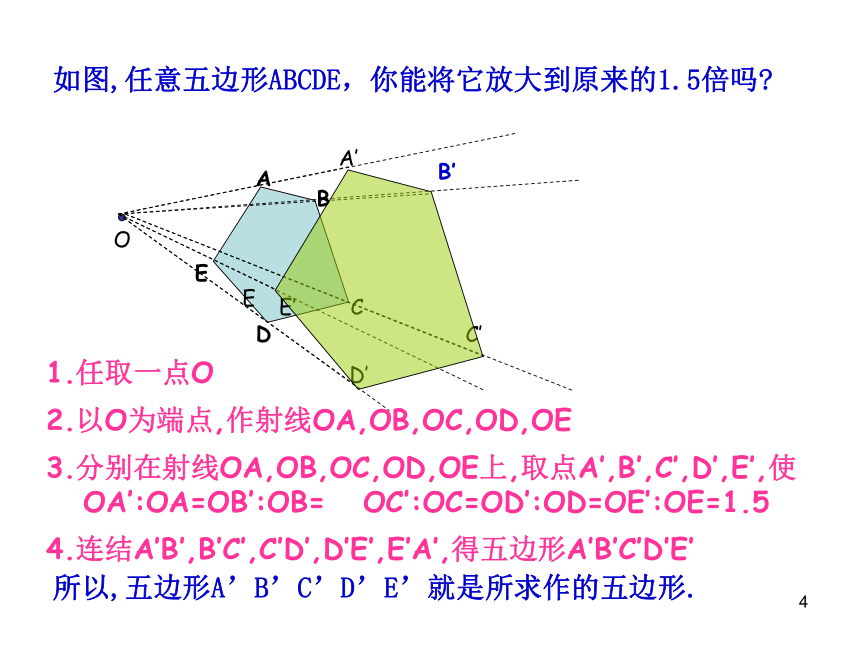
如图,任意五边形ABCDE,你能将它放大到原来的1.5倍吗
A
B
C
E
D
1.任取一点O
O
2.以O为端点,作射线OA,OB,OC,OD,OE
3.分别在射线OA,OB,OC,OD,OE上,取点A’,B’,C’,D’,E’,使
OA’:OA=OB’:OB= OC’:OC=OD’:OD=OE’:OE=1.5
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’
E
所以,五边形A’B’C’D’E’就是所求作的五边形.
*
A
B
C
E
D
O
A’
B’
C’
D’
E’
两图形中对应线段有什么关系 对应角呢
你能说明为什么吗
∴
∵OA’:OA=OB’:OB=1.5
且∠AOB=∠A’OB’
△AOB~△A’OB’
∴A’B’:AB=OA’:OA=1.5
同理:B’C’:BC=C’D’:CD=
D’E’:DE=E’A’:EA=A’B’:AB=1.5
∵△AOB~A’OB’, △AOE~△A’OE’
∴∠OAB=∠OA’B’, ∠OAE=∠OA’E’
∴∠EAB=∠E’A’B’
同理:
∠ABC=A’B’C’,∠BCD=∠B’C’D’, ∠CDE=∠C’D’E’,∠DEA=∠D’E’A’,
∴五边形ABCDE与五边形A’B’C’D’E’相似
观察对应点的连线有何特点
像这样两个多边形不仅相似,且对应点的连线相交于一点,像这样的相似叫做位似。这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.
位似是相似的特殊情况:
对应点的连线交于一点
两图形中对应线段成比例;对应角相等。
1.两个多边形相似;
2.对应点的连线相交于一点;
3.对应边平行或在同一直线上;
*
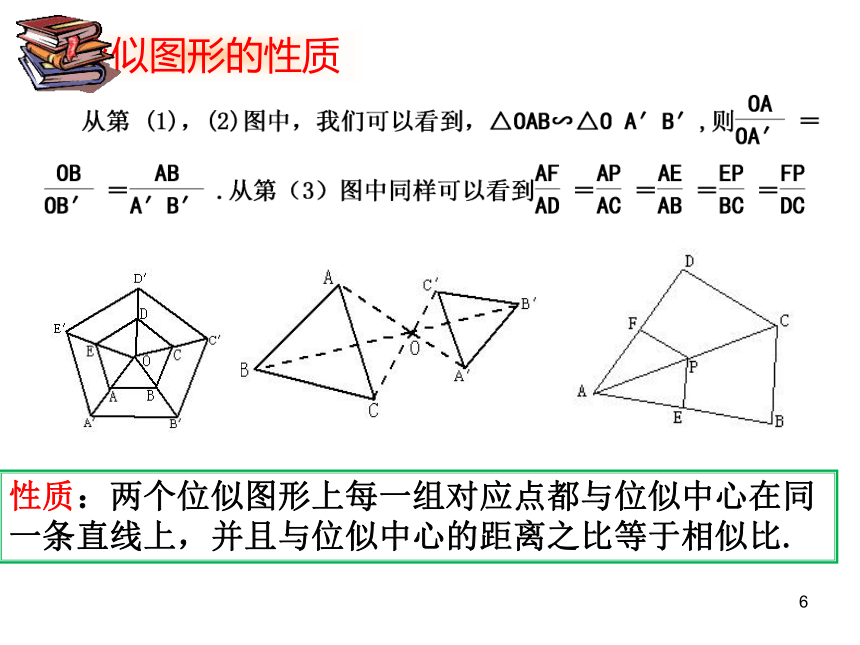
性质:两个位似图形上每一组对应点都与位似中心在同一条直线上,并且与位似中心的距离之比等于相似比.
位似图形的性质
*
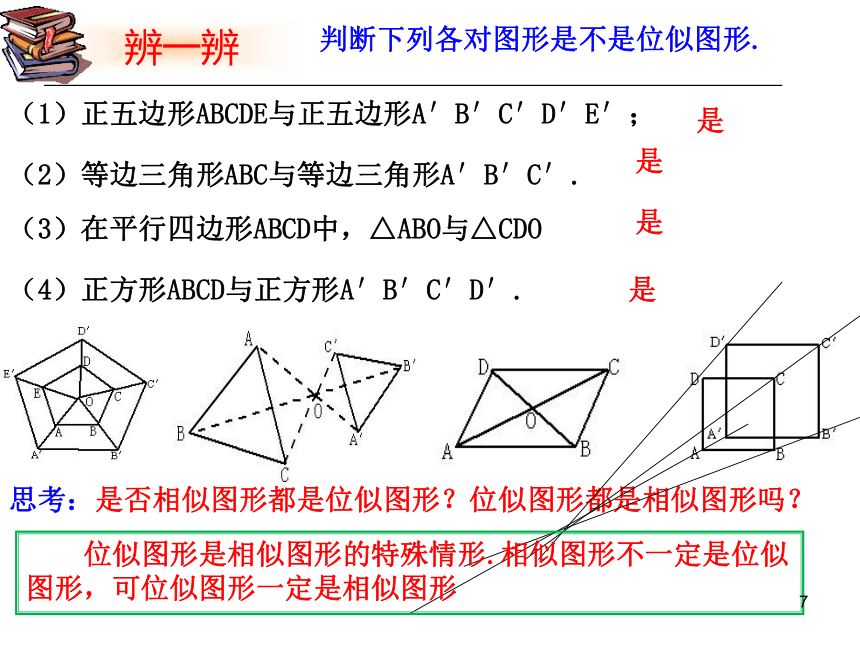
1. 判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
辨一辨
(2)等边三角形ABC与等边三角形A′B′C′.
思考:是否相似图形都是位似图形?位似图形都是相似图形吗?
是
是
(3)在平行四边形ABCD中,△ABO与△CDO
是
(4)正方形ABCD与正方形A′B′C′D′.
是
位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
*
O
O
例1:作出下列位似图形的位似中心:
*
观察下列三组图形,找出是位似图形,并指出位似中心
*
分析:将△ABC的三边缩小为原来的1/2:
O
A
B
C
做法:1.任取一点O ;
则△DEF就是所求
例2:作与△ABC的位似图形△DEF且位似比为1/2
F
●
E
●
D
●
3.连结D,E,F
2.连接AO,BO,CO,并取它们的中点D,E,F;
*
A
B
C
E
D
O
A’
B’
C’
D’
E’
观察所画的图,原图形和所画图形位于位似中心的
能位于位似中心的 吗
例:画四边形ABCD的相似图形,使得所画图形与原图形的相似比为
2:1,且位于位似中心的两侧.
A
B
C
D
O
A’
B’
C’
D’
*
C’
B’
A’
B’
C’
A’
B’
C’
A
B
C
位似中心是任意取的,那么除了把位似中心取在图形外,还可以取在那里
(2)图形内
例:将三角形ABC放大两倍
O
(3)多边形边上
A
B
C
A
B
C
.
O
(4)多边形顶点上
.
(O)
如果要将三角形ABC缩小到原来的一半,该怎么画 画一画.
位似中心不只是可以放在图形内部,外部,还可以放在多边形的顶点上,任意一边上。
*
D
A
E
B
C
O
A′
B′
C′
D′
E′
解:画图如下
∴五边形A’B’C’D’E’为所求
例3:将五边形ABCDE缩小为原来的
练习:1.任意画一个四边形,再把它缩小到原来的一半;
2.任意画一个五边形,再把它放大到原来的3倍;
*
例4:如果 OAB和 OCD是位似图形,那么AB∥CD吗?
为什么?
解:AB∥CD.理由是:
OAB和 OCD是位似图形,
OAB∽ OCD
∠OAB=∠C
AB∥CD.
A
B
C
D
O
*
1.由位似变换得到的图形与原图形是( )
A,全等 B ,相似 C,不一定相似 D ,肯定不全等。
B
2下列运动形式中:
(1)传动带上的电视机;(2)电梯上的人的升降;(3)照相时底上的投影与站在照相机前的人;(4)国旗上的红五角星;
上述运动形式中不是位似变换的有( )
A,0个 B,1个 C,2个 D3个。
C
3.下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等; B.两个图形如果是位似图形,那么这两个图形不一定相似; C.两个图形如果是相似图形,那么这两个图形一定位似; D.两个图形如果是位似图形,那么这两个图形一定相似。
D
*
课堂小结
1.位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
2.位似图形的特征:
相似; 对应点到位似中心的距离之比等于位似比;对应边平行或在同一直线上;
3.位似中心的位置
1.外部(同侧或者异侧) 2.内部
3.顶点上 4.任意一边上
4.画已知图形的位似图形时,要明确位似中心和位似比。
*
1.如图,AB与CD交于O,AC∥BD,若CO:CD= 1:4,AC=2cm,求BD;
O
A
B
C
D
(1)
2.如图,△ABC中,EF∥BC,EF:BC=1:3,且BF与CE相交于O,求FO:BO.
A
B
C
E
F
O
(2)
3.P72页习题24.5
课堂作业
*
华东师大版《数学 · 九年级(上)》
§24.5 画位似图形
一课时
*
三种基本变换
平移
旋转
轴对称
变换前后图形的形状和大小都未变
*
相似与轴对称,平移,旋转一样,也是图形之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
思考:相似图形需要具备哪些条件
对应角都相等,对应边都成比例
如何便捷的画出一个图形的相似图形呢
这节课我们学习画相似图形的一种特殊方法
*
如图,任意五边形ABCDE,你能将它放大到原来的1.5倍吗
A
B
C
E
D
1.任取一点O
O
2.以O为端点,作射线OA,OB,OC,OD,OE
3.分别在射线OA,OB,OC,OD,OE上,取点A’,B’,C’,D’,E’,使
OA’:OA=OB’:OB= OC’:OC=OD’:OD=OE’:OE=1.5
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’
E
所以,五边形A’B’C’D’E’就是所求作的五边形.
*
A
B
C
E
D
O
A’
B’
C’
D’
E’
两图形中对应线段有什么关系 对应角呢
你能说明为什么吗
∴
∵OA’:OA=OB’:OB=1.5
且∠AOB=∠A’OB’
△AOB~△A’OB’
∴A’B’:AB=OA’:OA=1.5
同理:B’C’:BC=C’D’:CD=
D’E’:DE=E’A’:EA=A’B’:AB=1.5
∵△AOB~A’OB’, △AOE~△A’OE’
∴∠OAB=∠OA’B’, ∠OAE=∠OA’E’
∴∠EAB=∠E’A’B’
同理:
∠ABC=A’B’C’,∠BCD=∠B’C’D’, ∠CDE=∠C’D’E’,∠DEA=∠D’E’A’,
∴五边形ABCDE与五边形A’B’C’D’E’相似
观察对应点的连线有何特点
像这样两个多边形不仅相似,且对应点的连线相交于一点,像这样的相似叫做位似。这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.
位似是相似的特殊情况:
对应点的连线交于一点
两图形中对应线段成比例;对应角相等。
1.两个多边形相似;
2.对应点的连线相交于一点;
3.对应边平行或在同一直线上;
*
性质:两个位似图形上每一组对应点都与位似中心在同一条直线上,并且与位似中心的距离之比等于相似比.
位似图形的性质
*
1. 判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
辨一辨
(2)等边三角形ABC与等边三角形A′B′C′.
思考:是否相似图形都是位似图形?位似图形都是相似图形吗?
是
是
(3)在平行四边形ABCD中,△ABO与△CDO
是
(4)正方形ABCD与正方形A′B′C′D′.
是
位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
*
O
O
例1:作出下列位似图形的位似中心:
*
观察下列三组图形,找出是位似图形,并指出位似中心
*
分析:将△ABC的三边缩小为原来的1/2:
O
A
B
C
做法:1.任取一点O ;
则△DEF就是所求
例2:作与△ABC的位似图形△DEF且位似比为1/2
F
●
E
●
D
●
3.连结D,E,F
2.连接AO,BO,CO,并取它们的中点D,E,F;
*
A
B
C
E
D
O
A’
B’
C’
D’
E’
观察所画的图,原图形和所画图形位于位似中心的
能位于位似中心的 吗
例:画四边形ABCD的相似图形,使得所画图形与原图形的相似比为
2:1,且位于位似中心的两侧.
A
B
C
D
O
A’
B’
C’
D’
*
C’
B’
A’
B’
C’
A’
B’
C’
A
B
C
位似中心是任意取的,那么除了把位似中心取在图形外,还可以取在那里
(2)图形内
例:将三角形ABC放大两倍
O
(3)多边形边上
A
B
C
A
B
C
.
O
(4)多边形顶点上
.
(O)
如果要将三角形ABC缩小到原来的一半,该怎么画 画一画.
位似中心不只是可以放在图形内部,外部,还可以放在多边形的顶点上,任意一边上。
*
D
A
E
B
C
O
A′
B′
C′
D′
E′
解:画图如下
∴五边形A’B’C’D’E’为所求
例3:将五边形ABCDE缩小为原来的
练习:1.任意画一个四边形,再把它缩小到原来的一半;
2.任意画一个五边形,再把它放大到原来的3倍;
*
例4:如果 OAB和 OCD是位似图形,那么AB∥CD吗?
为什么?
解:AB∥CD.理由是:
OAB和 OCD是位似图形,
OAB∽ OCD
∠OAB=∠C
AB∥CD.
A
B
C
D
O
*
1.由位似变换得到的图形与原图形是( )
A,全等 B ,相似 C,不一定相似 D ,肯定不全等。
B
2下列运动形式中:
(1)传动带上的电视机;(2)电梯上的人的升降;(3)照相时底上的投影与站在照相机前的人;(4)国旗上的红五角星;
上述运动形式中不是位似变换的有( )
A,0个 B,1个 C,2个 D3个。
C
3.下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等; B.两个图形如果是位似图形,那么这两个图形不一定相似; C.两个图形如果是相似图形,那么这两个图形一定位似; D.两个图形如果是位似图形,那么这两个图形一定相似。
D
*
课堂小结
1.位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
2.位似图形的特征:
相似; 对应点到位似中心的距离之比等于位似比;对应边平行或在同一直线上;
3.位似中心的位置
1.外部(同侧或者异侧) 2.内部
3.顶点上 4.任意一边上
4.画已知图形的位似图形时,要明确位似中心和位似比。
*
1.如图,AB与CD交于O,AC∥BD,若CO:CD= 1:4,AC=2cm,求BD;
O
A
B
C
D
(1)
2.如图,△ABC中,EF∥BC,EF:BC=1:3,且BF与CE相交于O,求FO:BO.
A
B
C
E
F
O
(2)
3.P72页习题24.5
课堂作业
*
