23.6 图形与坐标 课件(共20张PPT)
文档属性
| 名称 | 23.6 图形与坐标 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
*
华东师大版《数学 · 九年级(上)》
§24.6 图形与坐标
一课时
*
复 习
1.什么是平面直角坐标系
建立了平面直角坐标系后,平面的点可以用什么来描述
坐标平面上的点用有序实数对来描述它的位置,有序实数对就是我们常说的点的坐标;
2.画一个直角坐标系,并描出点A(1,2),B(-3, 5),C(4,5),D(0,3)的位置。
平面上画两条互相垂直的数轴,就组成了平面直角坐标系;
*
四座农舍的坐标是:
(1,2)
(-3,5)
(4,5)
(0,3)
农舍1
农舍4
农舍2
农舍3
·
·
·
·
·
A
点A为目的地的位置.
夏令营举行野外拉练活动,老师交给大家一张地图,如图所示,地图上画了一个直角坐标系,作为定向标记,给出了四座农舍的坐标是: (1, 2)、(-3, 5)、(4,5)、(0,3).
目的地位于连结第一与第三座农舍的直线和连结第二与第四座农舍的直线的交点.利用平面直角坐标系,同学们很快就到达了目的地.请你在图中画出目的地的位置.
*
图24.6.2是某乡镇的示意图.试建立直角坐标系,用坐标表示各地的位置:
*
1.如用经度和纬度来表示一个地点在地球上的位置;
2.电影院的座位用几排几座来表示;
3.国际象棋中竖条用字母表示,横条用数字表示等.
有了平面直角坐标系,我们可以毫不费力地在平面上确定一个点的位置.
请举出现实生活中这种方法的应用的例子:
*
E2
E3
E4
下图是国际象棋的棋盘,E2在什么位置 又如何描述A、B、C的位置
*
我们还可以用其他方式来表示物体的位置:
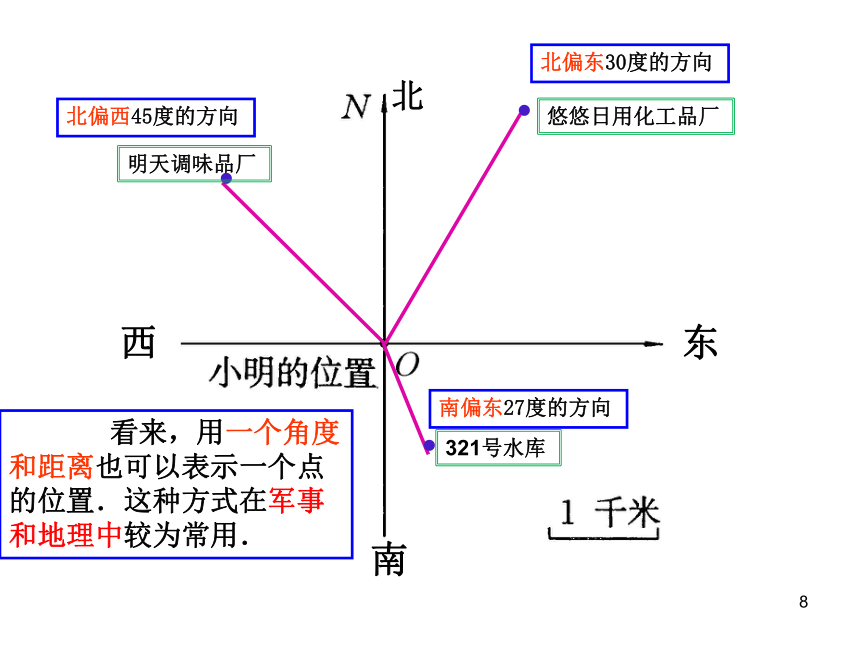
例如,小明去某地考察环境污染问题,并且他事先知道下面的信息:
“悠悠日用化工品厂”在他现在所在地的北偏东30度的方向,距离此处3千米的地方;
“明天调味品厂”在他现在所在地的北偏西45度的方向,距离此处2.4千米的地方;
“321号水库”在他现在所在地的南偏东27度的方向,距离此处1.1千米的地方.
根据这些信息可以画出表示各处位置的一张简图:
*
东
南
西
北
悠悠日用化工品厂
·
·
明天调味品厂
·
321号水库
看来,用一个角度和距离也可以表示一个点的位置.这种方式在军事和地理中较为常用.
北偏东30度的方向
北偏西45度的方向
南偏东27度的方向
*
1、相似三角形的相似比是2﹕3,则周长比是______.
2、小红坐在第 5 排 24 号用(5,24)表示,则
( 6,27)表示小红坐在第__排___号。
3、点A(3,-2)关于 x 轴对称的点是_____。
4、点A(3,4)关于 y 轴对称的点是_____。
5、P(2,3)关于原点对称的点是_____。
6、 P(-2,3)到x轴的距离是___。
7 、如图2矩形ABOC的长OB=3,
宽AB=2,则点A的坐标为 。
8、如果点P(a-3,a+4)在第二象限,
则a的取值范围是_____。
9、点A(a,- 4)到两坐标轴的距离相等,则a=_____.
-
A
C
B
O
x
y
(2)
口 答
2﹕3
6
27
(3,2)
(-3,4)
(-2,-3)
3
(-3,2)
-4±4
P76页练习
*
探索:如果是⊿AOB 向右移动3个单位长度,得到⊿A’O’B ’,各顶点的坐标又有什么变化?你能用自已的语言归纳这个规律吗?
A
0 B
想想:你如果⊿AOB向左移动时,对应点的坐标又有什么规律吗?
O’
B’
Y
X
A’
规律:图形左右平移,横坐标左减右加,纵坐标不变:
*
讨论:
A
0 2 4 B
将⊿AOB向下移动3个单位长度,你能探索出图形上下移动的规律吗?
规律:图形上下平移,横坐标不变,纵坐标上加下减.
Y
X
-5
4
想想:如果⊿AOB向上移动5个单位,对应点的坐标又有什么规律?
*
探索:将⊿AOB沿着x轴对折,得到⊿A ’ OB,画图并
说明对应顶点有什么变化规律?
O
规律:图形关于横轴对称
对应点横坐标相等,纵坐标互为相反数
Y
X
A
B
A’
*
0
规律:图形关于纵轴对称
对应点横坐标互为相反数;纵坐标相等
Y
X
A
B
C
C’
B’
A’
探索:画出⊿ABC,A(2,1),B(4,0),C(5,2)沿y 轴对折后的⊿A ’B’C ’,并观察对应顶点又有什么样的变化?
*
思考:画⊿AOB关于原点对称的⊿A’O B ’
你有什么发现?
0
规律:
图形关于原点对称:对应点的横坐标和纵坐标互为相反数
X
Y
A
B
B’
A’
*
探索:如果将⊿AOB缩小,变成⊿COD,它们的相似
比是多少?对应点的坐标有什么变化?
规律: 图形扩大或缩小
横坐标和纵坐标都变化相同的倍数。
X
6
2
0 2 6
Y
C
D
A
B
*
O
X
Y
4
-4
-2
A
B
C
2
4
-4
例:1.画出⊿ABC向下平移4个单位后的图形
2.画出⊿ABC关于原点对称的图形
3.以O为位似中心,将⊿ABC放大2倍
*
矩形公园ABCD的长宽分别是6 千米, 4千米 , 以公园中心为原点建立坐标系, 写出各顶点的坐标.找出各点的关系
B
C
D
A
解: 公园各顶点坐标为
A( 3 , 2), B( -3 , 2 ),
C( -3 , -2 ), D( 3 , -2 ) .
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数
点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数
点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数
*
B
C
D
A
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
思考:
1.由点B到点A是怎样移动得到的?他们坐标有何关系?
2.在图中,你还能看到哪些点的移动?
*
(1)平移 图形沿x轴平移,横变(左减右加)纵不变;
图形沿y轴平移,纵变(上加右减)横不变。
直角坐标系中,图形经过平移、对称、位似的变化,其对应平面的坐标也发生了变化,其变化规律为:
(2)对称 图形关于x轴对称,横不变,纵为相反数;
图形关于y轴对称,纵不变,横为相反数;
图形关于原点对称,横纵皆为相反数。
(3) 位似 以O为位似中心放大或缩小,横纵坐标都扩大或缩
小相同的倍数。
课堂小结:
*
1、
求出a的值.
已知点M
与点N
①
点M
关于x轴对称;
向右平移3个单位后落在y轴上;
点M
②
在第二象限角平分线上;
③
请根据下列条件分别
在第三象限,求a的整数值;
④
2.课本P78页习题
课堂作业:
*
华东师大版《数学 · 九年级(上)》
§24.6 图形与坐标
一课时
*
复 习
1.什么是平面直角坐标系
建立了平面直角坐标系后,平面的点可以用什么来描述
坐标平面上的点用有序实数对来描述它的位置,有序实数对就是我们常说的点的坐标;
2.画一个直角坐标系,并描出点A(1,2),B(-3, 5),C(4,5),D(0,3)的位置。
平面上画两条互相垂直的数轴,就组成了平面直角坐标系;
*
四座农舍的坐标是:
(1,2)
(-3,5)
(4,5)
(0,3)
农舍1
农舍4
农舍2
农舍3
·
·
·
·
·
A
点A为目的地的位置.
夏令营举行野外拉练活动,老师交给大家一张地图,如图所示,地图上画了一个直角坐标系,作为定向标记,给出了四座农舍的坐标是: (1, 2)、(-3, 5)、(4,5)、(0,3).
目的地位于连结第一与第三座农舍的直线和连结第二与第四座农舍的直线的交点.利用平面直角坐标系,同学们很快就到达了目的地.请你在图中画出目的地的位置.
*
图24.6.2是某乡镇的示意图.试建立直角坐标系,用坐标表示各地的位置:
*
1.如用经度和纬度来表示一个地点在地球上的位置;
2.电影院的座位用几排几座来表示;
3.国际象棋中竖条用字母表示,横条用数字表示等.
有了平面直角坐标系,我们可以毫不费力地在平面上确定一个点的位置.
请举出现实生活中这种方法的应用的例子:
*
E2
E3
E4
下图是国际象棋的棋盘,E2在什么位置 又如何描述A、B、C的位置
*
我们还可以用其他方式来表示物体的位置:
例如,小明去某地考察环境污染问题,并且他事先知道下面的信息:
“悠悠日用化工品厂”在他现在所在地的北偏东30度的方向,距离此处3千米的地方;
“明天调味品厂”在他现在所在地的北偏西45度的方向,距离此处2.4千米的地方;
“321号水库”在他现在所在地的南偏东27度的方向,距离此处1.1千米的地方.
根据这些信息可以画出表示各处位置的一张简图:
*
东
南
西
北
悠悠日用化工品厂
·
·
明天调味品厂
·
321号水库
看来,用一个角度和距离也可以表示一个点的位置.这种方式在军事和地理中较为常用.
北偏东30度的方向
北偏西45度的方向
南偏东27度的方向
*
1、相似三角形的相似比是2﹕3,则周长比是______.
2、小红坐在第 5 排 24 号用(5,24)表示,则
( 6,27)表示小红坐在第__排___号。
3、点A(3,-2)关于 x 轴对称的点是_____。
4、点A(3,4)关于 y 轴对称的点是_____。
5、P(2,3)关于原点对称的点是_____。
6、 P(-2,3)到x轴的距离是___。
7 、如图2矩形ABOC的长OB=3,
宽AB=2,则点A的坐标为 。
8、如果点P(a-3,a+4)在第二象限,
则a的取值范围是_____。
9、点A(a,- 4)到两坐标轴的距离相等,则a=_____.
-
A
C
B
O
x
y
(2)
口 答
2﹕3
6
27
(3,2)
(-3,4)
(-2,-3)
3
(-3,2)
-4
P76页练习
*
探索:如果是⊿AOB 向右移动3个单位长度,得到⊿A’O’B ’,各顶点的坐标又有什么变化?你能用自已的语言归纳这个规律吗?
A
0 B
想想:你如果⊿AOB向左移动时,对应点的坐标又有什么规律吗?
O’
B’
Y
X
A’
规律:图形左右平移,横坐标左减右加,纵坐标不变:
*
讨论:
A
0 2 4 B
将⊿AOB向下移动3个单位长度,你能探索出图形上下移动的规律吗?
规律:图形上下平移,横坐标不变,纵坐标上加下减.
Y
X
-5
4
想想:如果⊿AOB向上移动5个单位,对应点的坐标又有什么规律?
*
探索:将⊿AOB沿着x轴对折,得到⊿A ’ OB,画图并
说明对应顶点有什么变化规律?
O
规律:图形关于横轴对称
对应点横坐标相等,纵坐标互为相反数
Y
X
A
B
A’
*
0
规律:图形关于纵轴对称
对应点横坐标互为相反数;纵坐标相等
Y
X
A
B
C
C’
B’
A’
探索:画出⊿ABC,A(2,1),B(4,0),C(5,2)沿y 轴对折后的⊿A ’B’C ’,并观察对应顶点又有什么样的变化?
*
思考:画⊿AOB关于原点对称的⊿A’O B ’
你有什么发现?
0
规律:
图形关于原点对称:对应点的横坐标和纵坐标互为相反数
X
Y
A
B
B’
A’
*
探索:如果将⊿AOB缩小,变成⊿COD,它们的相似
比是多少?对应点的坐标有什么变化?
规律: 图形扩大或缩小
横坐标和纵坐标都变化相同的倍数。
X
6
2
0 2 6
Y
C
D
A
B
*
O
X
Y
4
-4
-2
A
B
C
2
4
-4
例:1.画出⊿ABC向下平移4个单位后的图形
2.画出⊿ABC关于原点对称的图形
3.以O为位似中心,将⊿ABC放大2倍
*
矩形公园ABCD的长宽分别是6 千米, 4千米 , 以公园中心为原点建立坐标系, 写出各顶点的坐标.找出各点的关系
B
C
D
A
解: 公园各顶点坐标为
A( 3 , 2), B( -3 , 2 ),
C( -3 , -2 ), D( 3 , -2 ) .
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数
点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数
点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数
*
B
C
D
A
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
思考:
1.由点B到点A是怎样移动得到的?他们坐标有何关系?
2.在图中,你还能看到哪些点的移动?
*
(1)平移 图形沿x轴平移,横变(左减右加)纵不变;
图形沿y轴平移,纵变(上加右减)横不变。
直角坐标系中,图形经过平移、对称、位似的变化,其对应平面的坐标也发生了变化,其变化规律为:
(2)对称 图形关于x轴对称,横不变,纵为相反数;
图形关于y轴对称,纵不变,横为相反数;
图形关于原点对称,横纵皆为相反数。
(3) 位似 以O为位似中心放大或缩小,横纵坐标都扩大或缩
小相同的倍数。
课堂小结:
*
1、
求出a的值.
已知点M
与点N
①
点M
关于x轴对称;
向右平移3个单位后落在y轴上;
点M
②
在第二象限角平分线上;
③
请根据下列条件分别
在第三象限,求a的整数值;
④
2.课本P78页习题
课堂作业:
