24.3.2解直角三角形 课件(共12张PPT)
文档属性
| 名称 | 24.3.2解直角三角形 课件(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 935.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 13:18:40 | ||
图片预览





文档简介
(共12张PPT)
*
华东师大版《数学 · 九年级(上)》
第二课时
§24.3.2解直角三角形
方位角
在直角三角形中,除直角外,由已知两元素,求其余未知元素的过程叫解直角三角形。
1.什么叫解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据有哪些
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
3、解直角三角形的类型有哪些
(1)一锐角与一边 (2)两条边
思考:什么叫方向角
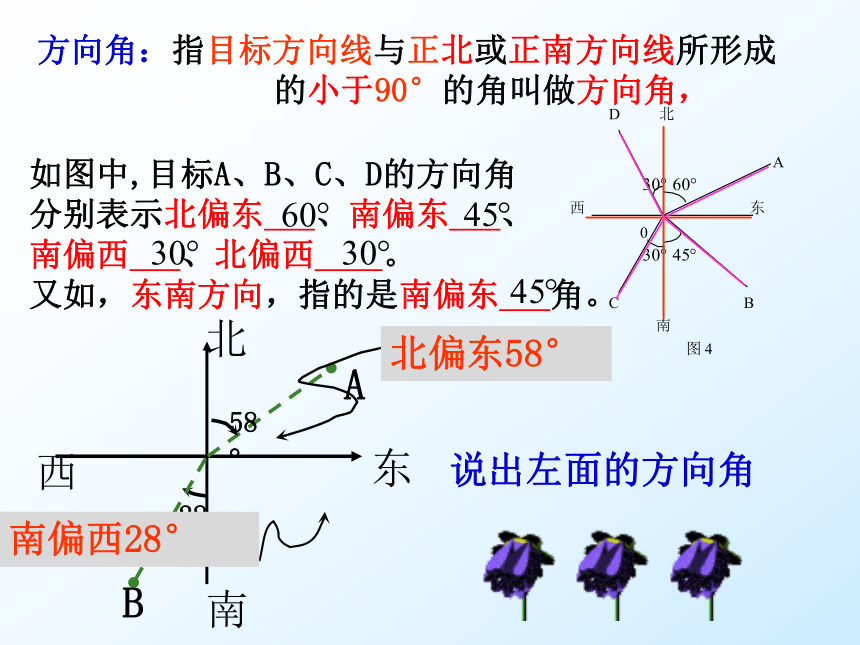
方向角:指目标方向线与正北或正南方向线所形成
的小于90°的角叫做方向角,
如图中,目标A、B、C、D的方向角
分别表示北偏东___、南偏东___、
南偏西___、北偏西____。
又如,东南方向,指的是南偏东___角。
北
东
西
南
A
58
28
B
南偏西28°
说出左面的方向角
北偏东58°
A
B
D
北
60°
E
320
160
200
120
∵BD=160海里<200海里
解:1.B城市会受到台风的影响。
作BD⊥AC于D。由题意知:∠BAC=30°,AB=320
∴B城市会受到台风的影响。
2.以B为圆心200海里为半径画圆与AC交于E、F两点:
F
由等腰三角形的性质和勾股定理知:
C
∴BD=160
练习:一渔船上的渔民在A处看见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离 ?
D
例2:正午10点整,一渔轮在小岛O的北偏东30方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60方向航行,那么渔轮到达小岛O的正东方向是什么时间?
O
A
30°
60 °
南
东
B
C
北
西
解:设渔轮达到C处时为正东方向
根据题意可得:
∠OAC=30°+60°=90°,
∠AOC=90°-30°=60°
∴tan60°=
∵A0=10
∴渔轮到达小岛O的正东方向是:
练习:如图,一艘海轮位于灯塔P的北偏东45°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?
45°
30°
P
B
C
A
练习:如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A、C两地的距离为
北
A
北
B
C
40海里
D
有一个角是600的等腰三角形是等边三角形
答:货轮无触礁危险。
在Rt△ADC中,
在Rt△ADB中,
∴AD≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
24海里
X
解得:X=12
设CD=x,则BD=X+24
例3:如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60 .在c见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
∵ tan∠DCA=
∴AD= tan600x=
∵ tan30 =
练习:海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
12
分析:只要求出A到BD的最最短距离是否在以A为圆心,以8海里的圆内或圆上即可。
【总结】
(1)试证明:点B在暗礁区外;
(2)若继续向东航行有无触暗礁的危险?
D
2.P95页练习第2题和P98习题第4题.
【作业】
解:1、证明.作CD⊥AB于D点,设BC为x。
在Rt△BCD中,∠CBD=60。
∴ BD= x CD= x
∠CAD=30tan∠CAD= =
∴ 解得 x=18
∴点B是在暗礁区域外。
2、∵CD= x =
∵ < 16
∴若继续向东航行有触礁的危险
*
华东师大版《数学 · 九年级(上)》
第二课时
§24.3.2解直角三角形
方位角
在直角三角形中,除直角外,由已知两元素,求其余未知元素的过程叫解直角三角形。
1.什么叫解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据有哪些
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
3、解直角三角形的类型有哪些
(1)一锐角与一边 (2)两条边
思考:什么叫方向角
方向角:指目标方向线与正北或正南方向线所形成
的小于90°的角叫做方向角,
如图中,目标A、B、C、D的方向角
分别表示北偏东___、南偏东___、
南偏西___、北偏西____。
又如,东南方向,指的是南偏东___角。
北
东
西
南
A
58
28
B
南偏西28°
说出左面的方向角
北偏东58°
A
B
D
北
60°
E
320
160
200
120
∵BD=160海里<200海里
解:1.B城市会受到台风的影响。
作BD⊥AC于D。由题意知:∠BAC=30°,AB=320
∴B城市会受到台风的影响。
2.以B为圆心200海里为半径画圆与AC交于E、F两点:
F
由等腰三角形的性质和勾股定理知:
C
∴BD=160
练习:一渔船上的渔民在A处看见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离 ?
D
例2:正午10点整,一渔轮在小岛O的北偏东30方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60方向航行,那么渔轮到达小岛O的正东方向是什么时间?
O
A
30°
60 °
南
东
B
C
北
西
解:设渔轮达到C处时为正东方向
根据题意可得:
∠OAC=30°+60°=90°,
∠AOC=90°-30°=60°
∴tan60°=
∵A0=10
∴渔轮到达小岛O的正东方向是:
练习:如图,一艘海轮位于灯塔P的北偏东45°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?
45°
30°
P
B
C
A
练习:如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A、C两地的距离为
北
A
北
B
C
40海里
D
有一个角是600的等腰三角形是等边三角形
答:货轮无触礁危险。
在Rt△ADC中,
在Rt△ADB中,
∴AD≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
24海里
X
解得:X=12
设CD=x,则BD=X+24
例3:如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60 .在c见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
∵ tan∠DCA=
∴AD= tan600x=
∵ tan30 =
练习:海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
12
分析:只要求出A到BD的最最短距离是否在以A为圆心,以8海里的圆内或圆上即可。
【总结】
(1)试证明:点B在暗礁区外;
(2)若继续向东航行有无触暗礁的危险?
D
2.P95页练习第2题和P98习题第4题.
【作业】
解:1、证明.作CD⊥AB于D点,设BC为x。
在Rt△BCD中,∠CBD=60。
∴ BD= x CD= x
∠CAD=30tan∠CAD= =
∴ 解得 x=18
∴点B是在暗礁区域外。
2、∵CD= x =
∵ < 16
∴若继续向东航行有触礁的危险
