7.2.5二元一次方程组解法小结5 课件(共11张PPT)
文档属性
| 名称 | 7.2.5二元一次方程组解法小结5 课件(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 426.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 09:50:40 | ||
图片预览



文档简介
(共11张PPT)
教师寄语——
不为失败找理由,只为成功找方法!这是人生的态度。人活着就应该有所追求,为了心中梦想的实现,我们惟有努力去寻找撬开成功大门的方法。
7.2.二元一次方程组解法复习
华东师大版《数学 · 七年级(下)》
第五课时
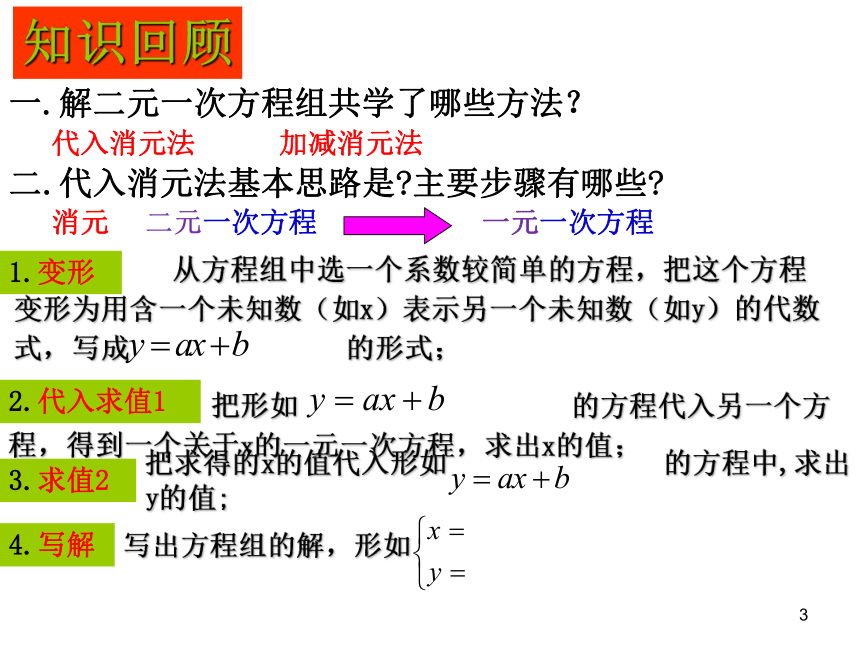
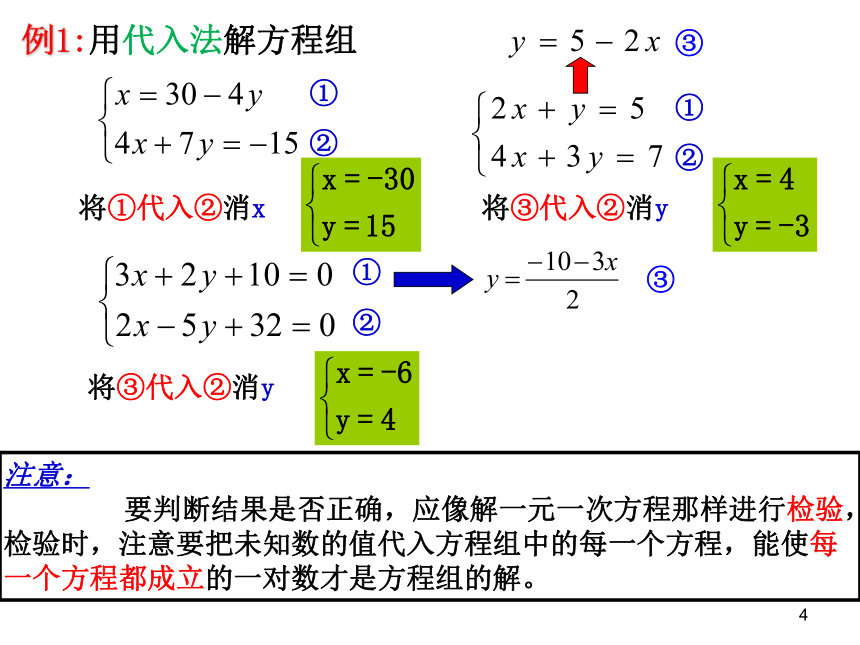
一.解二元一次方程组共学了哪些方法?代入消元法加减消元法二.代入消元法基本思路是 主要步骤有哪些 消元一元一次方程二元一次方程1.变形2.代入求值13.求值24.写解从方程组中选一个系数较简单的方程,把这个方程变形为用含一个未知数(如x)表示另一个未知数(如y)的代数式,写成的形式;把形如的方程代入另一个方程,得到一个关于x的一元一次方程,求出x的值;把求得的x的值代入形如的方程中,求出y的值;写出方程组的解,形如知识回顾例1:用代入法解方程组注意:要判断结果是否正确,应像解一元一次方程那样进行检验,检验时,注意要把未知数的值代入方程组中的每一个方程,能使每一个方程都成立的一对数才是方程组的解。将①代入②消x①②①②①②③将③代入②消y③将③代入②消y一.加减消元法基本思路是 消元一元一次方程二元一次方程1.变形:即处理系数思考:2.相加减:即求值13.代入:即求值24.写解写出方程组的解,形如二.加减消元法的 主要步骤有哪些 在标准形的二元一次方程组中,两个方程中相同的未知数的系数相同,或互为相反数。就可以把两个方程相减或相加。而达到消去一个未知数的目的,得到一个一元一次方程。通过两个方程相加或相减消去一个未知数,把二元一次方程组化为一元一次方程。并求的一个未知数的值。把这个未知数的值代入方程,求的另一个未知数的值。例2:用加减法解方程组:注意:两个方程中相同未知数的系数既不相同,也不相反时,可根据等式的性质2,选择适当的数去乘方程的两边,使之转化为步骤1所论的情形,再按步骤1进行。将①+②消y①②①②①②①②将①-②消x将①×2+②×3消y将①×2+②消y1.下列方程组各选择哪种消元法来解比较简便 y=2x3x-4y=52x+3y=212x-5y=59x-5y=17y+9x=2代入法加减法加减法想一想2.在解下列方程组时,下列方法中最简便的是( )13x-6y=25①27x-4y=19②A.代入法B.用①×27-②×13先消去xC.用①×4-②×6先消去y D.用①×2-②×3先消去yD3.你能用哪些方法解下列方程组 试一试.练一练:2x+5y= 1①3x-5y= 4 ②(1)x= 5y+2①4x+y = 29②(2)(3)2x-4y = 1①4x-3y = 7②将①+②消yx = 1y = -0.2将①代入②消xy = 1x = 7将①×2- ②消xy = 1x = 2.5例3:解方程组:①②8x + 15y = 5412x + 15y = 6解:①②将方程组变形得:即:-6x + 3y = 0y = 2将②代入①得:-6x + 3×2 = 0x = 1解:将方程组变形得:将①-②得:x = -128x - 12x = 48将x=-12代入①得:8×(-12)+15y=54y = 10试 一试基本思路:二元一元消 元小 结1.解二元一次方程组基本思路是什么?2.二元一次方程组解法有.代入法、加减法3.若方程组的其中一个方程的某个未知数的系数为1或-1时,用代入消元法消元比较方便。若方程组中两个方程的同一个未知数系数相等或互为相反数或成 整数倍时,用加减消元法消元比较简单。课堂作业1.课本P46页复习题A组第2题3-6小题;2.课本P46页复习题B组第8题;
教师寄语——
不为失败找理由,只为成功找方法!这是人生的态度。人活着就应该有所追求,为了心中梦想的实现,我们惟有努力去寻找撬开成功大门的方法。
7.2.二元一次方程组解法复习
华东师大版《数学 · 七年级(下)》
第五课时
一.解二元一次方程组共学了哪些方法?代入消元法加减消元法二.代入消元法基本思路是 主要步骤有哪些 消元一元一次方程二元一次方程1.变形2.代入求值13.求值24.写解从方程组中选一个系数较简单的方程,把这个方程变形为用含一个未知数(如x)表示另一个未知数(如y)的代数式,写成的形式;把形如的方程代入另一个方程,得到一个关于x的一元一次方程,求出x的值;把求得的x的值代入形如的方程中,求出y的值;写出方程组的解,形如知识回顾例1:用代入法解方程组注意:要判断结果是否正确,应像解一元一次方程那样进行检验,检验时,注意要把未知数的值代入方程组中的每一个方程,能使每一个方程都成立的一对数才是方程组的解。将①代入②消x①②①②①②③将③代入②消y③将③代入②消y一.加减消元法基本思路是 消元一元一次方程二元一次方程1.变形:即处理系数思考:2.相加减:即求值13.代入:即求值24.写解写出方程组的解,形如二.加减消元法的 主要步骤有哪些 在标准形的二元一次方程组中,两个方程中相同的未知数的系数相同,或互为相反数。就可以把两个方程相减或相加。而达到消去一个未知数的目的,得到一个一元一次方程。通过两个方程相加或相减消去一个未知数,把二元一次方程组化为一元一次方程。并求的一个未知数的值。把这个未知数的值代入方程,求的另一个未知数的值。例2:用加减法解方程组:注意:两个方程中相同未知数的系数既不相同,也不相反时,可根据等式的性质2,选择适当的数去乘方程的两边,使之转化为步骤1所论的情形,再按步骤1进行。将①+②消y①②①②①②①②将①-②消x将①×2+②×3消y将①×2+②消y1.下列方程组各选择哪种消元法来解比较简便 y=2x3x-4y=52x+3y=212x-5y=59x-5y=17y+9x=2代入法加减法加减法想一想2.在解下列方程组时,下列方法中最简便的是( )13x-6y=25①27x-4y=19②A.代入法B.用①×27-②×13先消去xC.用①×4-②×6先消去y D.用①×2-②×3先消去yD3.你能用哪些方法解下列方程组 试一试.练一练:2x+5y= 1①3x-5y= 4 ②(1)x= 5y+2①4x+y = 29②(2)(3)2x-4y = 1①4x-3y = 7②将①+②消yx = 1y = -0.2将①代入②消xy = 1x = 7将①×2- ②消xy = 1x = 2.5例3:解方程组:①②8x + 15y = 5412x + 15y = 6解:①②将方程组变形得:即:-6x + 3y = 0y = 2将②代入①得:-6x + 3×2 = 0x = 1解:将方程组变形得:将①-②得:x = -128x - 12x = 48将x=-12代入①得:8×(-12)+15y=54y = 10试 一试基本思路:二元一元消 元小 结1.解二元一次方程组基本思路是什么?2.二元一次方程组解法有.代入法、加减法3.若方程组的其中一个方程的某个未知数的系数为1或-1时,用代入消元法消元比较方便。若方程组中两个方程的同一个未知数系数相等或互为相反数或成 整数倍时,用加减消元法消元比较简单。课堂作业1.课本P46页复习题A组第2题3-6小题;2.课本P46页复习题B组第8题;
