第三章 圆 复习课(共24张PPT) 北师大版九年级下册数学
文档属性
| 名称 | 第三章 圆 复习课(共24张PPT) 北师大版九年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 21:57:39 | ||
图片预览







文档简介
(共24张PPT)
第三章 圆
第三章 复习课
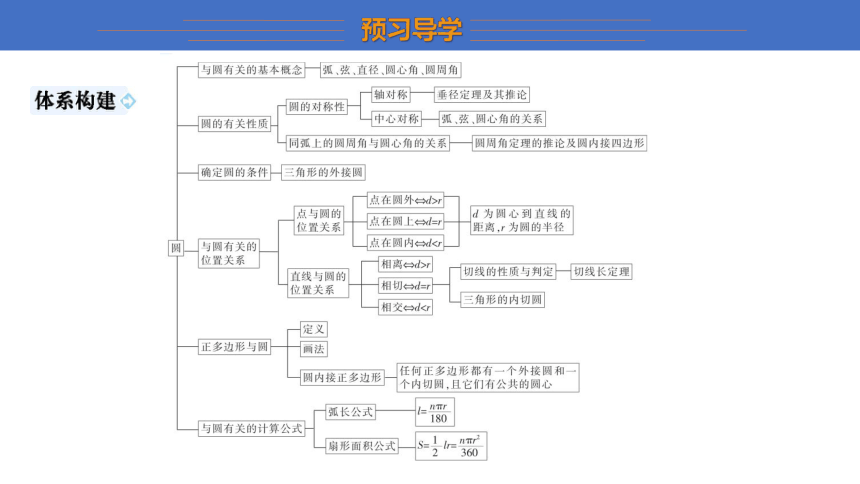
1.会利用垂径定理及其推论进行计算和证明.
2.知道弧、弦、圆心角、圆周角之间的关系,并能应用它们之间的关系进行推理和证明.
3.知道点与圆的位置关系、直线与圆的位置关系,并能判断这些位置关系,知道切线的性质和判定定理及切线长定理,并能应用其进行推理和计算.
4.会画三角形的外接圆和内切圆,知道三角形内心和外心的性质,知道圆内接多边形并会进行相关计算.
5.知道弧长和扇形面积的计算公式,并能用这些公式进行相关计算.
◎重点:圆有关性质的证明与计算、切线的性质和判定及利用弧长和扇形面积的公式计算.
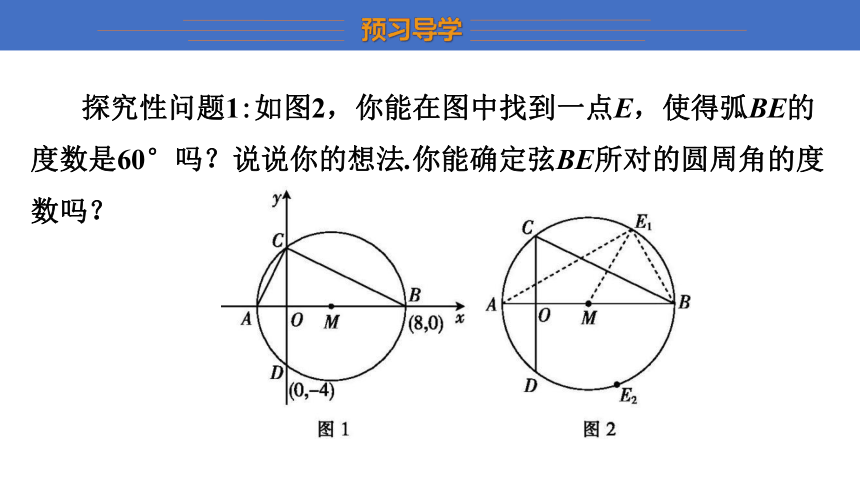
如图1,圆M的圆心在x轴上,与两坐标轴相交于点A、B、C、D,其中B点的坐标为(8,0),D点的坐标为(0,-4).想-想,根据已有信息,你能得到哪些结论?运用了哪些数学知识?
生:由D点的坐标(0,-4)及圆的对称性,我得到了C点的坐标为(0,4).
生:我可以计算出圆的半径为5.
生:数学知识:如直角三角形、等腰三角形.
师:你是怎么求的?数学依据是什么?
生:连接MD,勾股定理可以得到OM=3,圆的半径为5.
生:除了可以得到点的坐标外,我还能计算出线段AC的长度以及BC、AC的函数解析式等.
探究性问题1:如图2,你能在图中找到一点E,使得弧BE的度数是60°吗?说说你的想法.你能确定弦BE所对的圆周角的度数吗?
核心梳理
1.垂径定理及其推论.
(1)垂直于弦的直径 平分这条弦 ,并且平分这条弦所对的弧.
(2)平分弦(不是直径)的直径 垂直于弦 ,并且平分弦所对的弧.
平分这条弦
垂直于弦
2.圆周角、弦、弧之间的关系定理.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中 有一组量相等 ,那么它们所对应的其余各组量都 分别相等 .
有一组量相等
分别相
等
3.圆周角和圆心角的关系.
(1)一条弧所对的圆周角等于它所对的圆心角的 一半 .
(2)同弧或等弧所对的圆周角 相等 .
(3)直径所对的圆周角是 直角 ;90°的圆周角所对的弦是 直径 .
(4)圆内接四边形的对角 互补 .
一半
相等
直角
直径
互补
4.切线的性质和判定及切线长.
(1)圆的切线 垂直于 经过切点的半径.
(2)经过直径的一端,并且 垂直于 这条直径的直线是圆的切线.
(3)过圆外一点所画的圆的两条切线的 长相等 .
垂直于
垂直于
长相等
5.与圆有关的位置关系.
点和圆的位置关系 点到圆心的距离d与r的关系
点在圆外 d>r
点在圆上 d=r
点在圆内 d<r
d>r
d=r
d<r
直线和圆的位置关系 圆心到直线的距离d与r的关系
相离 d>r
相切 d=r
相交 d<r
d>r
d=r
d<r
6.与圆有关的计算公式:弧长l= ,扇形面积= = l·r .
·导学建议·
教学时要以本章知识网络图展开复习,对于垂径定理及其推论和切线长定理要特别留意,尽管是加“*”号的内容,但是也很有可能会考查.
l·r
圆的有关性质
1.如图,若AB是☉O的直径,CD是☉O的弦,∠ABD=58°,则∠BCD等于( B )
A.116°
B.32°
C.58°
D.64°
B
2.某蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16 m,半径OA=10 m,则高度CD为 4 m.
4
3.如图,已知OA、OB是☉O的半径,C是的中点,M、N分别为OA、OB的中点,求证:MC=NC.
证明:如图,连接OC.∵C是的中点,
∴=,∴∠AOC=∠COB.
∵点M、N分别是OA、BO的中点,
∴OM=OA,ON=OB.
∴=,∴∠AOC=∠COB.
∵点M、N分别是OA、BO的中点,
∴OM=OA,ON=OB.
∵OA=OB,∴OM=ON.
∵OC=OC,
∴△OCM≌△OCN.
∴MC=NC.
∵OA=OB,∴OM=ON.
∵OC=OC,
∴△OCM≌△OCN.
∴MC=NC.
与圆有关的位置关系
4.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心,以2 cm长为半径作圆,则☉C与AB的位置关系是 相离 .
相离
5.如图,☉O的半径为3 cm,点P到圆心的距离为6 cm,经过点P引☉O的两条切线,这两条切线的夹角为 60 度.
6.已知正三角形ABC的内心为I,则∠BIC的度数是 120 度.
60
120
7.如图,P为☉O直径延长线上一点,PC是☉O的切线,∠P=30°,求证:CA=CP.
证明:如图,连接OC.∵PC是☉O的切线,
∴∠OCP=90°,
∴∠COP=90°-∠P=60°.∵OA=OC,
∴∠A=∠OCA,
∴∠A=∠OCA,
∴∠A=∠COP=×60°=30°,
∴∠P=∠A,∴CA=CP.
与圆有关的计算
8.已知扇形的圆心角为120°,弧长为20π cm,求扇形的面积.(结果用π表示)
解:根据弧长公式得,=20π,解得R=30,
故S扇形=lR=×20π×30=300π(cm2).
方法归纳交流 在解决与圆有关的问题时,可以做的辅助线:
(1)当问题中存在同弧或等弧时,构造它们所对的圆周角是常用的辅助线,由此可得到相等的角;
(2)当图形中有直径时,“见直径,构造直径所对的圆周角”是常用的辅助线;
(3)当图形中有与半径垂直的线段时,常延长此线段与圆相交,这样可利用垂径定理得到相等的线段和相等的弧.
第三章 圆
第三章 复习课
1.会利用垂径定理及其推论进行计算和证明.
2.知道弧、弦、圆心角、圆周角之间的关系,并能应用它们之间的关系进行推理和证明.
3.知道点与圆的位置关系、直线与圆的位置关系,并能判断这些位置关系,知道切线的性质和判定定理及切线长定理,并能应用其进行推理和计算.
4.会画三角形的外接圆和内切圆,知道三角形内心和外心的性质,知道圆内接多边形并会进行相关计算.
5.知道弧长和扇形面积的计算公式,并能用这些公式进行相关计算.
◎重点:圆有关性质的证明与计算、切线的性质和判定及利用弧长和扇形面积的公式计算.
如图1,圆M的圆心在x轴上,与两坐标轴相交于点A、B、C、D,其中B点的坐标为(8,0),D点的坐标为(0,-4).想-想,根据已有信息,你能得到哪些结论?运用了哪些数学知识?
生:由D点的坐标(0,-4)及圆的对称性,我得到了C点的坐标为(0,4).
生:我可以计算出圆的半径为5.
生:数学知识:如直角三角形、等腰三角形.
师:你是怎么求的?数学依据是什么?
生:连接MD,勾股定理可以得到OM=3,圆的半径为5.
生:除了可以得到点的坐标外,我还能计算出线段AC的长度以及BC、AC的函数解析式等.
探究性问题1:如图2,你能在图中找到一点E,使得弧BE的度数是60°吗?说说你的想法.你能确定弦BE所对的圆周角的度数吗?
核心梳理
1.垂径定理及其推论.
(1)垂直于弦的直径 平分这条弦 ,并且平分这条弦所对的弧.
(2)平分弦(不是直径)的直径 垂直于弦 ,并且平分弦所对的弧.
平分这条弦
垂直于弦
2.圆周角、弦、弧之间的关系定理.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中 有一组量相等 ,那么它们所对应的其余各组量都 分别相等 .
有一组量相等
分别相
等
3.圆周角和圆心角的关系.
(1)一条弧所对的圆周角等于它所对的圆心角的 一半 .
(2)同弧或等弧所对的圆周角 相等 .
(3)直径所对的圆周角是 直角 ;90°的圆周角所对的弦是 直径 .
(4)圆内接四边形的对角 互补 .
一半
相等
直角
直径
互补
4.切线的性质和判定及切线长.
(1)圆的切线 垂直于 经过切点的半径.
(2)经过直径的一端,并且 垂直于 这条直径的直线是圆的切线.
(3)过圆外一点所画的圆的两条切线的 长相等 .
垂直于
垂直于
长相等
5.与圆有关的位置关系.
点和圆的位置关系 点到圆心的距离d与r的关系
点在圆外 d>r
点在圆上 d=r
点在圆内 d<r
d>r
d=r
d<r
直线和圆的位置关系 圆心到直线的距离d与r的关系
相离 d>r
相切 d=r
相交 d<r
d>r
d=r
d<r
6.与圆有关的计算公式:弧长l= ,扇形面积= = l·r .
·导学建议·
教学时要以本章知识网络图展开复习,对于垂径定理及其推论和切线长定理要特别留意,尽管是加“*”号的内容,但是也很有可能会考查.
l·r
圆的有关性质
1.如图,若AB是☉O的直径,CD是☉O的弦,∠ABD=58°,则∠BCD等于( B )
A.116°
B.32°
C.58°
D.64°
B
2.某蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16 m,半径OA=10 m,则高度CD为 4 m.
4
3.如图,已知OA、OB是☉O的半径,C是的中点,M、N分别为OA、OB的中点,求证:MC=NC.
证明:如图,连接OC.∵C是的中点,
∴=,∴∠AOC=∠COB.
∵点M、N分别是OA、BO的中点,
∴OM=OA,ON=OB.
∴=,∴∠AOC=∠COB.
∵点M、N分别是OA、BO的中点,
∴OM=OA,ON=OB.
∵OA=OB,∴OM=ON.
∵OC=OC,
∴△OCM≌△OCN.
∴MC=NC.
∵OA=OB,∴OM=ON.
∵OC=OC,
∴△OCM≌△OCN.
∴MC=NC.
与圆有关的位置关系
4.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心,以2 cm长为半径作圆,则☉C与AB的位置关系是 相离 .
相离
5.如图,☉O的半径为3 cm,点P到圆心的距离为6 cm,经过点P引☉O的两条切线,这两条切线的夹角为 60 度.
6.已知正三角形ABC的内心为I,则∠BIC的度数是 120 度.
60
120
7.如图,P为☉O直径延长线上一点,PC是☉O的切线,∠P=30°,求证:CA=CP.
证明:如图,连接OC.∵PC是☉O的切线,
∴∠OCP=90°,
∴∠COP=90°-∠P=60°.∵OA=OC,
∴∠A=∠OCA,
∴∠A=∠OCA,
∴∠A=∠COP=×60°=30°,
∴∠P=∠A,∴CA=CP.
与圆有关的计算
8.已知扇形的圆心角为120°,弧长为20π cm,求扇形的面积.(结果用π表示)
解:根据弧长公式得,=20π,解得R=30,
故S扇形=lR=×20π×30=300π(cm2).
方法归纳交流 在解决与圆有关的问题时,可以做的辅助线:
(1)当问题中存在同弧或等弧时,构造它们所对的圆周角是常用的辅助线,由此可得到相等的角;
(2)当图形中有直径时,“见直径,构造直径所对的圆周角”是常用的辅助线;
(3)当图形中有与半径垂直的线段时,常延长此线段与圆相交,这样可利用垂径定理得到相等的线段和相等的弧.
