3.8 圆内接正多边形课件(共18张PPT) 北师大版九年级下册数学
文档属性
| 名称 | 3.8 圆内接正多边形课件(共18张PPT) 北师大版九年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 927.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:58:02 | ||
图片预览






文档简介
(共18张PPT)
第三章 圆
8 圆内接正多边形
1.知道圆内接正多边形和正多边形外接圆的概念.
2.知道正多边形的中心、半径、中心角、边心距的概念.
3.会用直尺和圆规作出一些特殊的圆的内接正多边形.
◎重点:圆内接正多边形的有关计算与作用.
激趣导入
同学们,我们知道将一个圆等分n(n≥3)份后,可作出一个正n边形.如图,当这个多边形的边数不断增多时,你有何发现?圆的内接正多边形越来越接近该圆.中国数学家刘徽通过增加圆内接正多边形的数量来获取圆周率的正确数值,这种计算圆周率的方法就叫做“割圆术”.
圆内接正多边形的有关概念
阅读教材本课时相关内容,并回答下列问题.
1.顶点都在 同一圆上 的 正 多边形叫做圆内接正多边形,这个圆叫做该正多边形的 外接圆 .
同一圆上
正
外接圆
2.用尺规作一个已知圆的内接正四边形.
作法:(1)过圆心O作直径AC;
(2)用尺规作直径AC的垂直平分线,分别交圆于点B、D;
(3)依次连接AB、BC、CD、DA,就得到圆的内接正四边形ABCD.
1.若正方形的边长为6,则该正方形的边心距是 3 .
2.如图,四边形ABCD是☉O的内接正方形,P是上不同于点C的任意一点,则∠BPC的大小是( B )
3
B
A.22.5°
B.45°
C.30°
D.50°
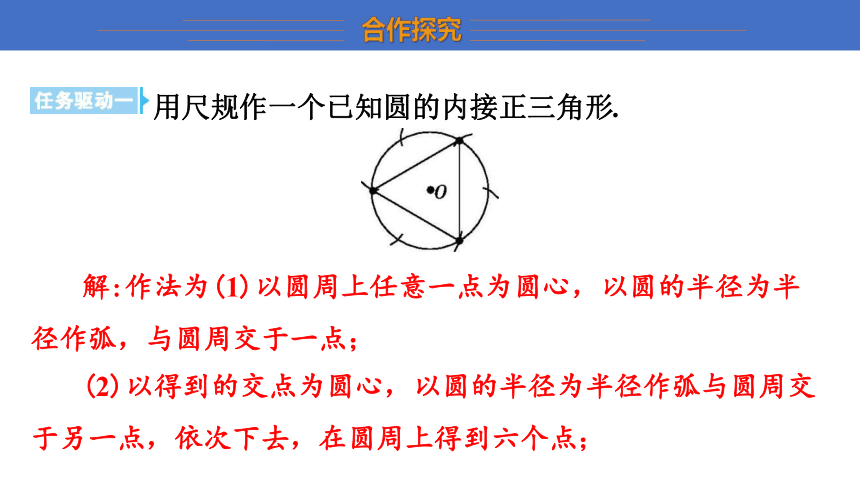
用尺规作一个已知圆的内接正三角形.
解:作法为(1)以圆周上任意一点为圆心,以圆的半径为半径作弧,与圆周交于一点;
(2)以得到的交点为圆心,以圆的半径为半径作弧与圆周交于另一点,依次下去,在圆周上得到六个点;
(3)依次每隔一点相连接,就得到了这个圆的一个内接正三角形.
已知正方形ABCD的边心距OE= cm,求这个正方形外接圆☉O的面积.
解:如图,连接OC、OD,
∵☉O是正方形ABCD的外接圆,∴O是对角线AC、BD的交点,
∴∠ODE=∠ADC=45°.
∴∠ODE=∠ADC=45°.
∵OE⊥CD,∴∠OED=90°,
∴∠DOE=180°-∠OED-ODE=45°,
∴OE=DE=,由勾股定理得OD==2,
∴这个正方形外接圆☉O的面积是π·2×2=4π.
答:这个正方形外接圆☉O的面积是4π.
∵OE⊥CD,∴∠OED=90°,
∴∠DOE=180°-∠OED-ODE=45°,
∴OE=DE=,由勾股定理得OD==2,
∴这个正方形外接圆☉O的面积是π·2×2=4π.
如图1、2、3、…、n,M、N分别是☉O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)求图1中∠MON的度数.
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:如图,(1)分别连接OB、OC,
∵AB=AC,∴∠ABC=∠ACB.
∵OC=OB,O是外接圆的圆心,
∴CO平分∠ACB,
∴∠OBC=∠OCB=30°,
∴∠OBM=∠OCN=30°.
∵BM=CN,OC=OB,∴△OMB≌△ONC,
∴∠BOM=∠NOC.
∵∠BAC=60°,∴∠BOC=120°,
∴∠MON=∠BOC=120°.
(2)90°,72°.
(3)∠MON=.
有一个亭子(如图),它的地基是半径为8 m的正六边形,求地基的周长和面积.(结果保留根号)
解:如图,连接OB、OC,
∵六边形ABCDEF是正六边形,
∴∠BOC==60°,
∴△OBC是等边三角形,
∴∠BOC==60°,
∴△OBC是等边三角形,
∴BC=OB=8 m,
∴正六边形ABCDEF的周长=6×8=48 m.
过O作OG⊥BC于G,
∵△OBC是等边三角形,OB=8 m,
∴∠OBC=60°,
∴OG=OB·sin∠OBC=8×=4 m,
∴S△OBC=BC·OG=×8×4=16 (m2),
过O作OG⊥BC于G,
∵△OBC是等边三角形,OB=8 m,
∴∠OBC=60°,
∴OG=OB·sin∠OBC=8×=4 m,
∴S△OBC=BC·OG=×8×4=16 (m2),
∴S正六边形ABCDEF=6S△OBC=6×16=96 m2.
第三章 圆
8 圆内接正多边形
1.知道圆内接正多边形和正多边形外接圆的概念.
2.知道正多边形的中心、半径、中心角、边心距的概念.
3.会用直尺和圆规作出一些特殊的圆的内接正多边形.
◎重点:圆内接正多边形的有关计算与作用.
激趣导入
同学们,我们知道将一个圆等分n(n≥3)份后,可作出一个正n边形.如图,当这个多边形的边数不断增多时,你有何发现?圆的内接正多边形越来越接近该圆.中国数学家刘徽通过增加圆内接正多边形的数量来获取圆周率的正确数值,这种计算圆周率的方法就叫做“割圆术”.
圆内接正多边形的有关概念
阅读教材本课时相关内容,并回答下列问题.
1.顶点都在 同一圆上 的 正 多边形叫做圆内接正多边形,这个圆叫做该正多边形的 外接圆 .
同一圆上
正
外接圆
2.用尺规作一个已知圆的内接正四边形.
作法:(1)过圆心O作直径AC;
(2)用尺规作直径AC的垂直平分线,分别交圆于点B、D;
(3)依次连接AB、BC、CD、DA,就得到圆的内接正四边形ABCD.
1.若正方形的边长为6,则该正方形的边心距是 3 .
2.如图,四边形ABCD是☉O的内接正方形,P是上不同于点C的任意一点,则∠BPC的大小是( B )
3
B
A.22.5°
B.45°
C.30°
D.50°
用尺规作一个已知圆的内接正三角形.
解:作法为(1)以圆周上任意一点为圆心,以圆的半径为半径作弧,与圆周交于一点;
(2)以得到的交点为圆心,以圆的半径为半径作弧与圆周交于另一点,依次下去,在圆周上得到六个点;
(3)依次每隔一点相连接,就得到了这个圆的一个内接正三角形.
已知正方形ABCD的边心距OE= cm,求这个正方形外接圆☉O的面积.
解:如图,连接OC、OD,
∵☉O是正方形ABCD的外接圆,∴O是对角线AC、BD的交点,
∴∠ODE=∠ADC=45°.
∴∠ODE=∠ADC=45°.
∵OE⊥CD,∴∠OED=90°,
∴∠DOE=180°-∠OED-ODE=45°,
∴OE=DE=,由勾股定理得OD==2,
∴这个正方形外接圆☉O的面积是π·2×2=4π.
答:这个正方形外接圆☉O的面积是4π.
∵OE⊥CD,∴∠OED=90°,
∴∠DOE=180°-∠OED-ODE=45°,
∴OE=DE=,由勾股定理得OD==2,
∴这个正方形外接圆☉O的面积是π·2×2=4π.
如图1、2、3、…、n,M、N分别是☉O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)求图1中∠MON的度数.
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:如图,(1)分别连接OB、OC,
∵AB=AC,∴∠ABC=∠ACB.
∵OC=OB,O是外接圆的圆心,
∴CO平分∠ACB,
∴∠OBC=∠OCB=30°,
∴∠OBM=∠OCN=30°.
∵BM=CN,OC=OB,∴△OMB≌△ONC,
∴∠BOM=∠NOC.
∵∠BAC=60°,∴∠BOC=120°,
∴∠MON=∠BOC=120°.
(2)90°,72°.
(3)∠MON=.
有一个亭子(如图),它的地基是半径为8 m的正六边形,求地基的周长和面积.(结果保留根号)
解:如图,连接OB、OC,
∵六边形ABCDEF是正六边形,
∴∠BOC==60°,
∴△OBC是等边三角形,
∴∠BOC==60°,
∴△OBC是等边三角形,
∴BC=OB=8 m,
∴正六边形ABCDEF的周长=6×8=48 m.
过O作OG⊥BC于G,
∵△OBC是等边三角形,OB=8 m,
∴∠OBC=60°,
∴OG=OB·sin∠OBC=8×=4 m,
∴S△OBC=BC·OG=×8×4=16 (m2),
过O作OG⊥BC于G,
∵△OBC是等边三角形,OB=8 m,
∴∠OBC=60°,
∴OG=OB·sin∠OBC=8×=4 m,
∴S△OBC=BC·OG=×8×4=16 (m2),
∴S正六边形ABCDEF=6S△OBC=6×16=96 m2.
