3.4 圆周角和圆心角的关系课件(共20张PPT) 第2课时 北师大版九年级下册数学
文档属性
| 名称 | 3.4 圆周角和圆心角的关系课件(共20张PPT) 第2课时 北师大版九年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 846.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 01:01:14 | ||
图片预览







文档简介
(共20张PPT)
第三章 圆
4 圆周角和圆心角的关系 第2课时
1.知道圆周角定理的推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径,并会利用其解决问题.
2.知道圆内接四边形及外接圆的概念,圆内接四边形的性质及相关应用.
3.经历探索的过程,进一步体会转化的思想以及分类归纳的思想方法.
◎重点:圆周角定理推论2与圆内接四边形的性质.
激趣导入
你喜欢看足球比赛吗?你踢过足球吗?
如图,甲队员在圆心O处,乙队员在圆上C处,丙队员带球突破防守到圆上C处,依然把球传给了甲,你知道为什么吗?你能用数学知识解释一下吗?
圆周角定理的推论2
阅读教材本课时“议一议”前面的内容,并回答下列问题.
在 同圆或等圆 中,同弧或等弧所对的 圆周角 相等.
同圆或等圆
圆周角
圆内接四边形
阅读教材本课时“议一议”及其后面的内容,回答下列问题.
(1)圆内接四边形的对角 互补 ;(2)圆内接四边形的一个角的外角等于这个角的 对角 .
互补
对角
·导学建议·
教学时让学生先独立思考,然后再进行交流,要鼓励学生说理方式的多样性;尽量让学生自己得出一个结论:圆内接四边形的任何一个外角都等于它的内对角.
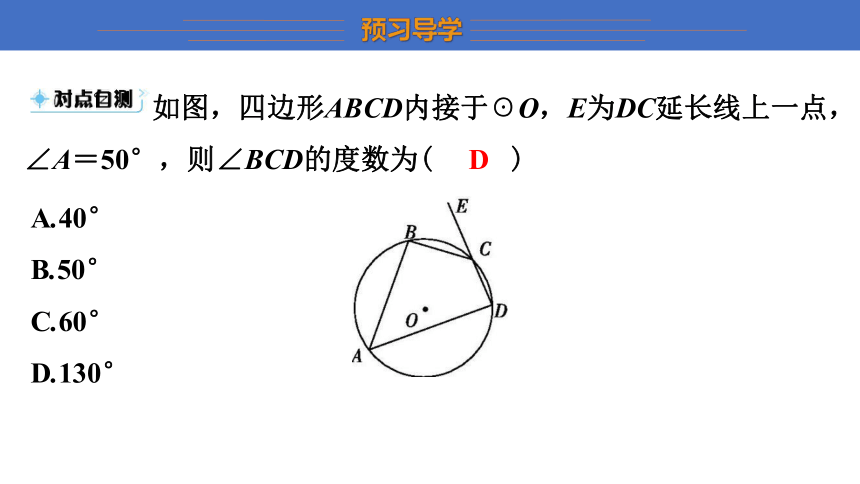
如图,四边形ABCD内接于☉O,E为DC延长线上一点,∠A=50°,则∠BCD的度数为( D )
D
A.40°
B.50°
C.60°
D.130°
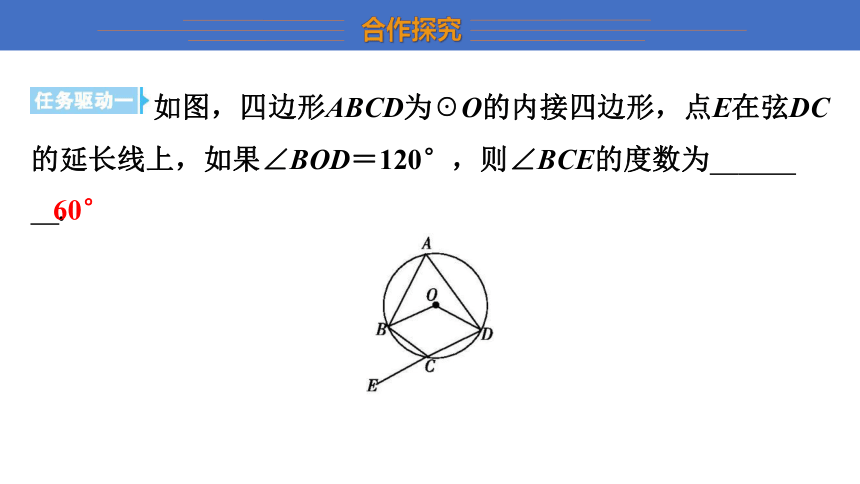
如图,四边形ABCD为☉O的内接四边形,点E在弦DC的延长线上,如果∠BOD=120°,则∠BCE的度数为 60° .
60°
如图,☉O是正方形ABCD的外接圆,点P在☉O上,则∠APB= 45° .
45°
如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF,求证:AB=AC.
证明:∵四边形ABCD内接于圆,
∴∠ABC+∠ADC=180°.
又∵∠CDE+∠ADC=180°,
∴∠ABC=∠CDE.
∵DE平分∠CDF,∴∠CDE=∠EDF.
∵∠ACB=∠ADB,∠ADB=∠EDF,
∴∠ACB=∠EDF,
∴∠ABC=∠ACB,∴AB=AC.
如图,已知AB为☉O的直径,AC为弦,OD∥BC,交AC于D,BC=4 cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sin A-1=0,求☉O的直径.
解:(1)证明:∵AB是☉O的直径,∴∠C=90°.
∵OD∥BC,∴∠ADO=∠C=90°.∴AC⊥OD.
(2)∵OD∥BC,又∵O是AB的中点,
∴点D是AC的中点,
∴OD是△ABC的中位线.
∴OD=BC=×4=2.
(3)∵2sin A-1=0,∴sin A=.∴∠A=30°.
在Rt△ABC中,∠A=30°,
∴BC=AB,∴AB=2BC=8.
即☉O的直径是8 cm.
如图,四边形ABCD是以O为圆心,AB为直径的半圆的内接四边形,对角线AC、BD相交于点E.
(1)求证:△DEC∽△AEB.
(2)当∠AED=60°时,求△DEC与△AEB的面积比.
解:(1)证明:∵∠CDE=∠EAB,∠DCE=∠EBA,
∴△DEC∽△AEB.
(2)∵AB是直径,∴∠ADB=90°.
∵∠AED=60°,∴∠DAE=30°.
∴AE=2DE.
∴S△DEC∶S△AEB=DE2∶AE2=1∶4.
1.如图,AB是☉O的直径,∠ACD=15°,则∠BAD的度数为( D )
A.15°
B.30°
C.60°
D.75°
D
2.如图,ABCD是☉O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD·DC=PA·BC.
证明:如图,连接BD.
∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB,
∴△PAD∽△DCB,
得PA∶DC=AD∶BC,
即AD·DC=PA·BC.
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB,
∴△PAD∽△DCB,
得PA∶DC=AD∶BC,
即AD·DC=PA·BC.
第三章 圆
4 圆周角和圆心角的关系 第2课时
1.知道圆周角定理的推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径,并会利用其解决问题.
2.知道圆内接四边形及外接圆的概念,圆内接四边形的性质及相关应用.
3.经历探索的过程,进一步体会转化的思想以及分类归纳的思想方法.
◎重点:圆周角定理推论2与圆内接四边形的性质.
激趣导入
你喜欢看足球比赛吗?你踢过足球吗?
如图,甲队员在圆心O处,乙队员在圆上C处,丙队员带球突破防守到圆上C处,依然把球传给了甲,你知道为什么吗?你能用数学知识解释一下吗?
圆周角定理的推论2
阅读教材本课时“议一议”前面的内容,并回答下列问题.
在 同圆或等圆 中,同弧或等弧所对的 圆周角 相等.
同圆或等圆
圆周角
圆内接四边形
阅读教材本课时“议一议”及其后面的内容,回答下列问题.
(1)圆内接四边形的对角 互补 ;(2)圆内接四边形的一个角的外角等于这个角的 对角 .
互补
对角
·导学建议·
教学时让学生先独立思考,然后再进行交流,要鼓励学生说理方式的多样性;尽量让学生自己得出一个结论:圆内接四边形的任何一个外角都等于它的内对角.
如图,四边形ABCD内接于☉O,E为DC延长线上一点,∠A=50°,则∠BCD的度数为( D )
D
A.40°
B.50°
C.60°
D.130°
如图,四边形ABCD为☉O的内接四边形,点E在弦DC的延长线上,如果∠BOD=120°,则∠BCE的度数为 60° .
60°
如图,☉O是正方形ABCD的外接圆,点P在☉O上,则∠APB= 45° .
45°
如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF,求证:AB=AC.
证明:∵四边形ABCD内接于圆,
∴∠ABC+∠ADC=180°.
又∵∠CDE+∠ADC=180°,
∴∠ABC=∠CDE.
∵DE平分∠CDF,∴∠CDE=∠EDF.
∵∠ACB=∠ADB,∠ADB=∠EDF,
∴∠ACB=∠EDF,
∴∠ABC=∠ACB,∴AB=AC.
如图,已知AB为☉O的直径,AC为弦,OD∥BC,交AC于D,BC=4 cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sin A-1=0,求☉O的直径.
解:(1)证明:∵AB是☉O的直径,∴∠C=90°.
∵OD∥BC,∴∠ADO=∠C=90°.∴AC⊥OD.
(2)∵OD∥BC,又∵O是AB的中点,
∴点D是AC的中点,
∴OD是△ABC的中位线.
∴OD=BC=×4=2.
(3)∵2sin A-1=0,∴sin A=.∴∠A=30°.
在Rt△ABC中,∠A=30°,
∴BC=AB,∴AB=2BC=8.
即☉O的直径是8 cm.
如图,四边形ABCD是以O为圆心,AB为直径的半圆的内接四边形,对角线AC、BD相交于点E.
(1)求证:△DEC∽△AEB.
(2)当∠AED=60°时,求△DEC与△AEB的面积比.
解:(1)证明:∵∠CDE=∠EAB,∠DCE=∠EBA,
∴△DEC∽△AEB.
(2)∵AB是直径,∴∠ADB=90°.
∵∠AED=60°,∴∠DAE=30°.
∴AE=2DE.
∴S△DEC∶S△AEB=DE2∶AE2=1∶4.
1.如图,AB是☉O的直径,∠ACD=15°,则∠BAD的度数为( D )
A.15°
B.30°
C.60°
D.75°
D
2.如图,ABCD是☉O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD·DC=PA·BC.
证明:如图,连接BD.
∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB,
∴△PAD∽△DCB,
得PA∶DC=AD∶BC,
即AD·DC=PA·BC.
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB,
∴△PAD∽△DCB,
得PA∶DC=AD∶BC,
即AD·DC=PA·BC.
